Установившиеся процессы в линейных электрических цепях

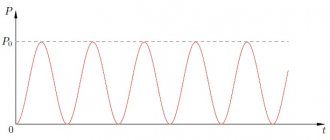
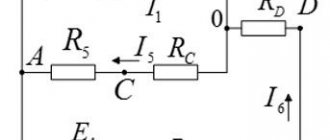
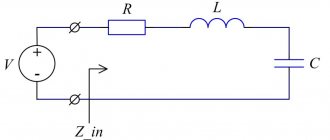
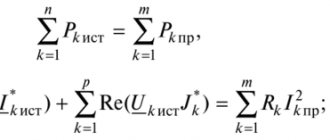В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

Введем понятие полного сопротивления цепи переменному току — Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока

На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Электрическая цепь.

Источник электрического тока, соединенный проводами с различными электроприборами и потребителями электри­ческой энергии, образует электрическую цепь.

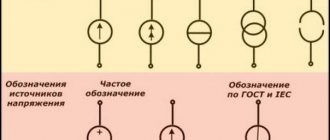
Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления, источники тока, включатели, лампы, при­боры и т. д.) обозначены специальными значками.

Направление тока в цепи — это направление от положи­тельного полюса источника тока к отрицательному. Это пра­вило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с ус­ловным направлением тока. Так, в металлах носителями тока являются отрицательно заряжен­ные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заря­да — положительные или отрицательные.

Включение элементов в электрическую цепь может быть последовательным или параллельным.

Ссылки [ править ]

1. Callegaro, стр. 2
2. Callegaro, Sec. 1.6
3. Наука
   , стр. 18, 1888 г.
4. Оливер Хевисайд, Электрик
   , стр. 212, 23 июля 1886 г., перепечатано как «
   Электрические документы», том II
   , стр. 64, книжный магазин AMS, ISBN 0-8218-3465-7
5. Kennelly, Артур. Импеданс
   (AIEE, 1893)
6. Александр, Чарльз; Садику, Мэтью (2006). Основы электрических цепей
   (3, перераб.). Макгроу-Хилл. С. 387–389. ISBN 978-0-07-330115-0 .
7. Комплексный импеданс , Гиперфизика
8. Горовиц, Пол; Хилл, Уинфилд (1989). «1» . Искусство электроники
   . Издательство Кембриджского университета. С. 31–32 . ISBN 978-0-521-37095-0 .
9. Закон AC Ома , Гиперфизика
10. Горовиц, Пол; Хилл, Уинфилд (1989). «1» . Искусство электроники
    . Издательство Кембриджского университета. С. 32–33 . ISBN 978-0-521-37095-0 .
11. Параллельные выражения импеданса , Гиперфизика
12. ^ ab
    Джордж Льюис-младший; Джордж К. Льюис старший и Уильям Ольбрихт (август 2008 г.). «Экономичная широкополосная схема измерения электрического импеданса и анализ сигналов для пьезоматериалов и ультразвуковых преобразователей» .
    Измерительная наука и технология
    .
    19
    (10): 105102. Bibcode : 2008MeScT..19j5102L . DOI : 10.1088 / 0957-0233 / 19/10/105102 . PMC 2600501 . PMID 19081773 .

Что такое сопротивление

Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.

Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.

См. Также [ править ]

• Анализ биоэлектрического импеданса
• Характеристический импеданс — отношение амплитуд напряжения и тока одиночной волны, распространяющейся по линии передачи.
• Электрические характеристики динамических громкоговорителей
• Высокий импеданс
• Иммитанс
• Анализатор импеданса
• Мостовое сопротивление
• Кардиография импеданса
• Контроль импеданса
• Согласование импеданса
• Импедансная микробиология
• Конвертер отрицательного импеданса
• Расстояние сопротивления
• Импеданс линии передачи — явление сигнала
• Универсальный диэлектрический отклик

Виды сопротивления

В электротехнике рассматривается активное электрическое сопротивление, а также две разновидности реактивного: индуктивное и ёмкостное.

Активное сопротивление Можно представить себе электрическую цепь, в которой к клеммам батарейки через провод последовательно присоединены резистор и электрическая лампочка. Если замкнуть провода, лампочка загорится. Можно использовать вольтметр или мультиметр в соответствующем режиме работы, с помощью которых измеряется разность потенциалов между двумя точками цепи.

Измерив напряжение между клеммами и сравнив его с тем, которое имеется на проводах подсоединённых к лампочке, можно увидеть, что последнее меньше. Это связано с падением напряжения на впаянной в цепь радиодетали. Последняя оказывает противодействие электрическому току, затрудняя его прохождение.

Активным сопротивлением обладает каждая деталь, через которую проходит ток. У металлических проводов оно очень маленькое. Чтобы узнать величину сопротивления радиодетали, нужно изучить обозначение на ее корпусе. Если из рассматриваемой электроцепи убрать резистор, то сила тока, проходящего через лампочку, увеличится.

Формула для расчета активного сопротивления соответствует закону Ома:

R = U / I, где

• R — величина активного сопротивления между двумя точками в цепи;
• U — напряжение или разность потенциалов между ними;
• I — сила тока на рассматриваемом участке цепи.

Для расчета активного сопротивления проводника формула будет другая:

где K-коэффициент поверхностного эффекта, который равен 1,

• l — длина проводника,
• s — площадь поперечного сечения,
• p — “ро” удельное сопротивление.

Сопротивление принято измерять в Омах. Оно существенно зависит от формы и размеров объекта, через который протекает ток: сечения, длины, материала, а также от температуры. Действие активного сопротивления уменьшает энергию электрического тока, превращая её в другие формы (преимущественно в тепловую).

Реактивное сопротивление

Этот вид возникает тогда, когда переменный ток проходит сквозь элемент, который обладает индуктивностью или емкостью. Основной особенностью реактивного сопротивления является преобразование электрической энергии в другую форму в прямом и обратном направлениях. Часто это происходит циклически. Реактивное сопротивление проявляется только при изменениях силы тока и напряжения. Существует два его вида: индуктивное и емкостное.

Индуктивное сопротивление

При увеличении силы тока порождается магнитное поле, обладающее различными характеристиками. Наиболее важной из них является индуктивность. Магнитное поле, в свою очередь, воздействует на проводник, по которому протекает ток. Влияние является противоположным направлению изменения тока. То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.

Индуктивное сопротивление зависит от частоты тока. Чем она выше, тем выше скорость изменения данного параметра. Это значит, что будет образовано более сильное магнитное поле. Возникающая при этом ЭДС препятствует изменению электрического тока.

Расчет реактивного индуктивного сопротивления осуществляется по такой формуле:

XL = L×w = L×2π×f, где буквами обозначаются:

• L — индуктивность магнитного поля, которое порождается изменением силы тока;
• W — круговая частота изменения, которая используется в описании синусоидального изменения силы тока;
• Π — число «пи»;
• f — частота тока в обычном смысле.

При синусоидальном изменении напряжения сила тока будет меняться, отставая от него по фазе. Поэтому реактивное сопротивление трансформатора существенно зависит от его индуктивности.

Емкостное сопротивление

Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.

После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.

Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.

Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.

На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.

Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:

XС = 1/(w×C) = 1/(2π×f×C), где

• C — ёмкость используемого конденсатора;
• w — круговая частота переменного тока;
• π — число «пи»;
• f — частота переменного тока.

В рассматриваемом случае изменения тока отстают от напряжения.

Полное сопротивление

При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах. Оно способствует превращению части электрической энергии в нагрев. Реактивное сопротивление возникает лишь в цепи переменного тока. Чтобы определить его величину, необходимо из индуктивного вычесть ёмкостное. Эта характеристика показывает энергию, которая пульсирует в цепи, переходя из одной формы в другую.

Полное сопротивление представляет собой сумму активного и реактивного сопротивления в цепи переменного тока, но такое сложение необходимо выполнять особым образом. Для этого нужно начертить прямоугольный треугольник, катеты в котором должны иметь длину, равную величине активного и реактивного сопротивлений соответственно.

Будет интересно➡ Что такое автотрансформатор?

Длина гипотенузы будет численно выражать полное сопротивление электрической цепи. Для его определения используется правило, говорящее о том, что сумма квадратов катетов равна квадрату гипотенузы. Это правило называют теоремой Пифагора. Следовательно, формула, с помощью которой можно найти полное сопротивление, выглядит так:

Z = √(R^2+〖(XL-XC)〗^2 ), где

• Z — полное сопротивление;
• R — величина активной составляющей;
• XL и XC — значение индуктивного и емкостного параметра соответственно.

Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.

Измерение [ править ]

Измерение импеданса устройств и линий передачи — практическая задача в радиотехнике и других областях. Измерения импеданса можно проводить на одной частоте, или может представлять интерес изменение импеданса устройства в диапазоне частот. Импеданс может быть измерен или отображен непосредственно в омах, или могут отображаться другие значения, относящиеся к импедансу; например, в радиоантенне коэффициент стоячей волны или коэффициент отражения могут быть более полезными, чем только импеданс. Измерение импеданса требует измерения величины напряжения и тока, а также разности фаз между ними. Импеданс часто измеряют «мостовыми» методами.аналогично мосту Уитстона постоянного тока ; калиброванный эталонный импеданс регулируется, чтобы уравновесить влияние импеданса тестируемого устройства. Измерение импеданса в силовых электронных устройствах может потребовать одновременного измерения и подачи питания на работающее устройство.

Импеданс устройства можно рассчитать сложным делением напряжения и тока. Импеданс устройства можно рассчитать, приложив синусоидальное напряжение к устройству последовательно с резистором и измерив напряжение на резисторе и на устройстве. Выполнение этого измерения путем качания частот подаваемого сигнала позволяет получить фазу и величину импеданса. [12]

Использование импульсной характеристики может использоваться в сочетании с быстрым преобразованием Фурье (БПФ) для быстрого измерения электрического импеданса различных электрических устройств. [12]

Измеритель иммитанса (Индуктивность (L), емкости (С) и сопротивление (R)) , представляет собой устройство , обычно используется для измерения индуктивности, сопротивления и емкости компонента; по этим значениям можно рассчитать импеданс на любой частоте.

Пример [ править ]

Рассмотрим контур резервуара LC . Комплексный импеданс цепи равен

Z ( ω ) = j ω L 1 − ω 2 L C . {\displaystyle Z(\omega )={j\omega L \over 1-\omega ^{2}LC}.}

Сразу видно, что значение минимально (фактически равно 0 в данном случае) всякий раз, когда 1 | Z | {\displaystyle {1 \over |Z|}}

ω 2 L C = 1. {\displaystyle \omega ^{2}LC=1.}

Следовательно, угловая частота основного резонанса равна

ω = 1 L C . {\displaystyle \omega ={1 \over {\sqrt {LC}}}.}

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

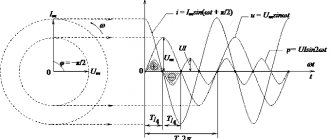
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.

Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.

Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.

Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

(1)

Извлекая квадратный корень из обеих частей этого равенства, получим,

(2)

Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.

Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.

В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) – схема цепи; б) – треугольник сопротивлений.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.

Для данного случая:

(3)

В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

(4)

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).

После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

(5)

Или

(6)

Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

СОДЕРЖАНИЕ

• 1 Введение
• 2 Комплексное сопротивление
• 3 Комплексное напряжение и ток 3.1 Действительность комплексного представления
• 3.2 Закон Ома
• 3.3 Фазоры

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.

Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

(7)

Приводя к общему знаменателю подкоренное выражение, получим:

(8)

откуда:

(9)

Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С будет равно:

(10)

Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.

В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.

Будет интересно➡ Что такое фаза в электричестве?

Формула полного сопротивления для этого случая будет:

(11)

Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

(12)

В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие

(13)

При соблюдении этого условия полное сопротивление колебательного контура будет равно:

(14)

где L—индуктивность катушки в Гн;

С—емкость конденсатора в Ф;

R—активное сопротивление катушки в Ом.

Закон Ома для полной цепи.

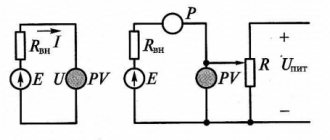
Рассмотрим электрическую цепь, состоящую из источника тока и ре­зистора R.

Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоя­щим из внешнего сопротивления R и внутреннего сопротивления источ­ника тока r.

Работа сторонних сил Aст источника тока, согласно определению ЭДС (ɛ) равна Aст = ɛq, где q — заряд, перемещенный ЭДС. Согласно определе­нию тока q = It, где t — время, в течение которого переносился заряд. Отсюда имеем:

Aст =ɛIt.

Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца, равно:

Q = I2Rt + I2rt.

Согласно закону сохранения энергии А = Q. Приравнивая (Aст =ɛIt) и (Q = I2Rt + I2rt), получим:

ɛ = IR + Ir.

Закон Ома для замкнутой цепи обычно записывается в виде:

.

Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Если цепь содержит несколько последовательно соединенных ис­точников с ЭДС ɛ1, ɛ2, ɛ3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.

Сторонние силы внутри источника совершают при этом по­ложительную работу. И наоборот, для цепи справедливо следующее уравнение:

ɛ = ɛ1 + ɛ2 + ɛ3 = | ɛ1| – | ɛ2| -| ɛ3| .

В соответствии с сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:

Rn = R + r1 + r2 + r3.

Переменный импеданс

Смотрите также: Сетевой анализ (электрические схемы) § Изменяющиеся во времени компоненты

В общем, ни импеданс, ни адмитанс не могут изменяться со временем, поскольку они определены для комплексных экспонент, в которых -∞ < т

< +∞. Если комплексное экспоненциальное отношение напряжения к току изменяется во времени или по амплитуде, элемент схемы не может быть описан с использованием частотной области. Однако многие компоненты и системы (например, варикапсы которые используются в радио тюнеры) может иметь нелинейное или изменяющееся во времени отношение напряжения к току, которое кажется линейный инвариантный во времени (LTI) для небольших сигналов и для небольших окон наблюдения, поэтому их можно грубо описать как если бы они имели изменяющийся во времени импеданс. Это описание является приблизительным: при больших колебаниях сигнала или широких окнах наблюдения отношение напряжения к току не будет LTI и не может быть описано импедансом.

Как измерить полное электрическое сопротивление

Соединим все детали вместе в простую электрическую цепь. Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.

Простая цепь постоянного тока с резистором

на 100 Ом для ограничения силы тока Что произойдет, если мы добавим в электрическую цепь источник питания переменного тока, катушку индуктивности и конденсатор? Теперь в цепи есть два дополнительных компонента, каждый из которых по своему оказывает сопротивление электрическому току. Как и резистор, они оба препятствуют прохождению электрического тока, при этом также воздействуют на ток. Если суммировать активное сопротивление резистора и активное и реактивное сопротивления конденсатора и катушки индуктивности, то получится полное электрическое сопротивление или импеданс.

В цепи переменного тока последовательно соединены резистор, катушка индуктивности и конденсатора

Постойте! Чтобы рассчитать полное электрическое сопротивления недостаточно просто сложить активные и реактивные сопротивления. Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.

Для чего она нужна и где используется

Подобные элементы находят множество применений, но наиболее часто они используются в качестве:

• Элементов индуктивности в слаботочных электрических цепях;
• Реакторов в силовой электронике, в качестве элементов компенсации реактивного характера нагрузки;
• Дросселей для сглаживания пульсаций выпрямленного или переменного тока;
• Электромагнитов в качестве источников магнитного поля в электромагнитных реле или органах управления различных устройств;
• Индукторов в установках индукционного нагрева;
• Накопителя энергии в источниках преобразования напряжения;
• Датчиков магнитных полей (магнитные головки в накопителях на жестких магнитных дисках);
• Линий задержки сигнала;
• Антенн для приема и передачи электромагнитных волн.

Индуктивная антенна

Практическое применение полного электрического сопротивления

Становится понятно, в конце концов, что после всех наших объяснений разобраться, что такое полное электрическое сопротивление, несложно, не так ли? Существуют десятки бесплатных калькуляторов , которые помогут вам выполнить расчеты. Что вам на самом деле нужно – это знать, что полное сопротивление работает так же, как активное сопротивление, ограничивая ток в цепи переменного тока.

Способность таких компонентов, как конденсаторы и катушки индуктивности реагировать на постоянные изменения переменного тока, делает их уникальными. Благодаря полному сопротивлению в вашей цепи можно организовать нечто похожее на электрический щит с защитными автоматами, которые реагируют на неожиданные скачки электричества, защищая от выгорания домашнюю электропроводку. Можно также сказать спасибо полному сопротивлению за то, что вы можете носить с собой ноутбук с полностью заряженным аккумулятором, не опасаясь его взрыва.

Когда дело доходит до работы с устройствами с питанием от источника переменного тока, будь то ноутбук или электрощит в вашем доме, стоит быть благодарным полному электрическому сопротивлению. И помните, полное электрическое сопротивление – это просто старший брат привычного активного сопротивления, который объединяет активное и реактивное сопротивления в одной простой формуле.

Комплексный импеданс

Графическое представление плоскость комплексного импеданса
Импеданс двухконтактного элемента схемы представлен как сложный количество Z { displaystyle Z} . В полярная форма удобно фиксирует как амплитудные, так и фазовые характеристики как

Z = | Z | е j аргумент ⁡ ( Z ) { Displaystyle Z = | Z | е ^ {j arg (Z)}}

где величина | Z | { displaystyle | Z |} представляет собой отношение амплитуды разности напряжений к амплитуде тока, а аргумент аргумент ⁡ ( Z ) { Displaystyle arg (Z)} (обычно обозначается символом θ { displaystyle theta} ) дает разность фаз между напряжением и током. j { displaystyle j} это мнимая единица, и используется вместо я { displaystyle i} в этом контексте, чтобы избежать путаницы с символом электрический ток.

В Декартова форма, импеданс определяется как

Z = р + j Икс { Displaystyle Z = R + jX}

где реальная часть импеданса это сопротивление р { displaystyle R} и мнимая часть это реактивное сопротивление Икс { displaystyle X} .

Там, где необходимо добавить или вычесть импедансы, более удобна декартова форма; но когда количества умножаются или делятся, расчет становится проще, если используется полярная форма. Расчет схемы, такой как определение полного импеданса двух параллельных импедансов, может потребовать преобразования между формами несколько раз во время расчета. Преобразование между формами происходит по обычному правила преобразования комплексных чисел.

Расчёт индуктивного сопротивления катушки

Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.

Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:

где:

• u0 – магнитная проницаемость вакуума – 4p*10-7 Гн/м;
• ur – относительная проницаемость сердечника;
• N – количество витков дросселя;
• S – его поперечное сечение в м2;
• l – длина катушки в метрах.

Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.

Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.