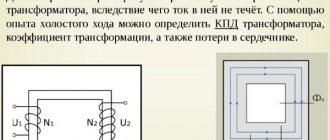
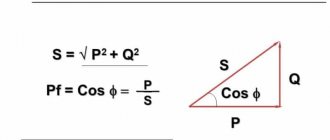
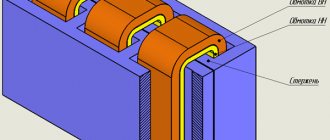
Всем доброго времени суток! В прошлой статье я рассказал об эквивалентной схеме трансформатора. В данной статье я расскажу, как рассчитать потери мощности в трансформаторе. От потерь мощности в трансформаторе зависит температура его нагрева, поэтому они значительно влияют на расчётные параметры. При расчёте трансформатора следует ограничивать потери мощности путем правильного выбора параметров и величин, влияющих на потери.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Составляющие потерь мощности в трансформаторе
Полные или суммарные потери мощности в трансформаторе ∆р состоят в основном из двух частей: потерь в сердечнике ∆рс и потерь в катушках ∆рк. Присутствующие потери мощности в элементах конструкций трансформатора имеют достаточно малое значение и обычно не учитываются.
При расчёте трансформатора, кроме вышеназванных величин, важное значение имеет соотношение потерь мощности ν и отношение суммарных потерь мощности ∆р к выходной мощности Р2, называемое коэффициентом потерь kпот
Довольно часто потери мощности ∆рс и ∆рк называют потерями «в стали» и потерями «в меди», однако это не совсем правильно, так как в качестве материала сердечника используются не только стали, но и различные сплавов, а в качестве материала проводов обмоток – не только медные, но и алюминий.
Потери мощности в катушках ∆рк, кроме основной части – потерь в обмотках – включает в себя потери в диэлектрике: изоляции проводника, межслоевой и межобмоточной ∆рд. Однако, данный компонент потерь мощности начинает влиять на общие потери, только у высоковольтных высокочастотных трансформаторов. Рассмотрим составляющие потерь мощности трансформатора.
Расчет потери реактивной мощности в трансформаторе.
Суммарные потери реактивной мощности силового трансформатора формируют:
- реактивная мощность намагничивания магнитопровода холостого хода Q0 = Qхх = Sн*Iхх/100, где Sн – номинальная мощность трансформатора (см. расчет мощности трансформатора в этом материале), Iхх – ток холостого хода в % по паспортным данным или справочнику;
- реактивная мощность полей рассеяния Qр = Sн*Кз²*Uкз/100, где Uкз – напряжение короткого замыкания в %, Кз – коэффициент загрузки, который определяется отношением полной мощности загрузки трансформатора к его номинальной мощности Sп/Sт.
Суммарные потери реактивной мощности трансформатора Qпт = Sн*Iхх/100 + Sн*Кз²*Uкз/100 = Sн*Iхх/100 + Кз²*Uкз/100).
Потери мощности в сердечнике трансформатора
В сердечнике ∆рс трансформатора потери мощности обусловлены затратами энергии магнитного поля на перемагничивание материала из которого сделан сердечник.
Энергия магнитного поля в общем случае определяется следующим выражением
где EC(t) – изменение напряжения за один период,
i(t) – изменение тока за один период.
В соответствие с законом электромагнитной индукции и теоремой о циркуляции вектора напряженности магнитного поля получим
где S – площадь поперечного сечения магнитопровода,
lcp – средняя длина магнитной силовой линии.
Так как ферромагнитные сердечники обладают гистерезисом, то однозначной функциональной зависимости между напряженностью Н и индукцией В магнитного поля в нем не существует. Однако при перемагничивании сердечника от –Нmax до Нmax можно считать, что любой величине напряженности магнитного поля Н соответствует только два значения магнитной индукции В: на восходящей и нисходящей ветвях. То есть, после полного цикла перемагничивания ферромагнетик вернётся в тоже состояние, из которого начинался процесс. Тогда подынтегральное выражение имеет физический смысл теплоты, отданной сердечником за один цикл перемегничивания.
Физический смысл магнитных потерь в сердечнике.
Так как потери мощности в сердечнике ∆рс определяется, как работа за единицу времени, то преобразовав предыдущую формулу, получим выражение для вычисления потерь мощности в сердечнике
где f – частота перемагничивания магнитопровода.
Подынтегральное выражение численно равно площади заштрихованного участка петли гистерезиса. Таким образом, вычисление данного интеграла является вычислением удельных потерь.
На практике нет необходимости в вычислении удельных потерь, так как для разработанных ферромагнитных материалов существуют справочные данные. Поэтому используют различные формулы в зависимости от известных справочных данных.
Достаточно широко распространено следующее выражение для высокочастотных материалов, где удельные потери имеют размерность Вт/(см3Гц)
PSV – удельные объемные потери в магнитопроводе,
Ve – эквивалентный объем сердечника магнитопровода,
f – частота перемагничивания.
Так для отечественных ферритов значение удельных объемных потерь составляют
| Марка феррита | PSV, мкВт/(см3*Гц), на частоте 10-20кГц | При индукции В, Тл | ||
| Т, °С | ||||
| +25 | +100 | +120 | ||
| 2500НМС1 | 10,5 | 8,7 | — | 0,2 |
| 2500НМС2 | 8,5 | 6 | — | 0,2 |
| 2500НМС5 | 9,0 | 7,6 | — | 0,2 (при 100 кГц) |
| 3000НМС | 2,5 | — | 2,5 | 0,1 |
Кроме данного выражения существуют более сложные способы вычисления потерь мощности в сердечнике трансформатора. Часто в справочниках приводятся удельные объемные потери PSV в Вт/см3 или удельные массовые потери PSM в Вт/кг. В этом случае потери мощности рассчитываются по следующим выражениям
где ρ – плотность материала,
f1, B1 – базовые расчётные параметры, при которых были измерены потери мощности в сердечнике,
α и β – степенные параметры, зависящие от конкретного материала, их значение можно найти в справочниках.
| Материал | PSV Вт/см3 | α | β |
| 2000НМ-А | 0,142 | 1,2 | 2,4 |
| 2000НМ-17 | 0,272 | 1,2 | 2,8 |
| 3000НМ-А | 0,208 | 1,2 | 2,8 |
| 1500НМ3 | 0,093 | 1,2 | 2,2 |
| 2000НМ3 | 0,178 | 1,3 | 2,7 |
Для данных материалов В1 = 1 Тл, f1 = 1 кГц.
| Материал | Толщина, мм | PSM, Вт/кг | α | β |
| 34НКМП | 0,1 | 2,2 | 1,65 | 1,7 |
| 40НКМП | 0,05 | 2,8 | 1,5 | 1,3 |
| 50НП | 0,1 | 5 | 1,4 | 1,5 |
| 79НМ | 0,1 | 1,4 | 1,65 | 2,0 |
| 68НМП | 0,05 | 2,2 | 1,55 | 1,7 |
| 80НХС | 0,05 | 1,2 | 1,5 | 2,0 |
Для данных материалов В1 = 0,5 Тл, f1 = 1 кГц.
Для ферритов иностранного производства выпускаются довольно подробные справочные материалы. Для расчета потерь в сердечниках из этих ферритов используется коэффициент удельных объемных потерь PV (Relative core losses) измеряемый в кВт/м3. Для этого параметра приводятся подробные графические зависимости от частоты f, магнитной индукции В и температуры Т.
Зависимость удельных потерь PV для феррита N72 от различных параметров.
Поэтому для нахождения потерь мощности для сердечников из таких материалов достаточно воспользоваться следующим выражением
где PV – удельные объемные потери в конкретных условиях,
Ve – эффективный объем сердечника.
Пример 1 – Определение потери напряжения, когда нагрузка подключена в конце линии
Определить потерю напряжения в трехфазной воздушной линии с номинальным напряжением Uном.=10 кВ протяженностью l = 2 км, питающей электрооборудование коммунального предприятия мощностью Р=100 кВт. Коэффициент мощности нагрузки cosϕ = 0,8. Линия выполнена алюминиевыми проводами марки А-25 сечением 25 мм2, расстояние между фазами 600 мм.
Решение.
1. Определяем активное сопротивление провода марки А-25:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
Также вы можете встретить в тех. литературе еще одну формулу по определению активного сопротивления провода (кабеля):
где:
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].
2. Определяем индуктивное сопротивление для провода марки А-25 [Л1.с.420]:
где:
- Дср. – среднее геометрическое расстояние между осями проводов, мм;
- d = 6,40 мм – диаметр провода, для марки провода А-25. Значение диаметра провода можно определить по ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. В данном расчете я привожу значение диаметра провода, только для провода марки А, для остальных марок проводов значения диаметров проводов вы сможете найти непосредственно в самом ГОСТе;
- µ — относительная магнитная проницаемость для цветных металлов (немагнитных) равна 1, для стальных проводов µ может достигать значений 103 и даже больше.
2.1 Определяем среднее геометрическое расстояние между осями трех проводов проложенных в одной плоскости [Л1.с.419]:
где: расстояние между проводами первой и второй фазы Д1-2= 600 мм, между второй и третью Д2-3 = 600 мм, между первой и третью Д1-3= 600 + 25 + 600 = 1225 мм.
3. Определяем коэффициент мощности tgϕ, зная cosϕ:
4. Определяем потерю напряжения в линии [Л1.с.422]:
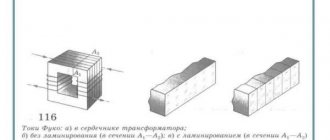
Как рассчитать потери мощности в наборных сердечниках?
Удельные потери магнитного материала в наборных сердечниках превышают аналогичные у прессованных. Причиной увеличения потерь является негативное влияние технологических операций при изготовлении сердечников. Для учета данного влияния вводят коэффициент увеличения потерь kp:
где Рсн – удельные потери мощности в наборном (ленточном или шихтованном) сердечнике,
РV/ – удельные потери материала, из которого изготовлены пластины или ленты сердечника,
kp – коэффициент увеличения потерь.
Значения данного коэффициента зависят от технологии изготовления, вида материала, рабочей частоты и вида сердечника. Так для наборных сердечников (ЛС и ШС) из электротехнической стали определяется следующим выражением
А для разрезных ленточных сердечников из железоникелевых сплавов
где ψа – параметр учитывающий тип сердечника. Для разъёмных сердечников (СТ, БТ) ψа = 3, а для замкнутых (ТТ) составляет ψа = 1.
В таблице ниже приведены типовые значения коэффициента увеличения потерь
| Тип сердечника | Материал | Значения kp при частоте в Гц | ||||
| Вид | Толщина | 50 | 400 | 2000 | 10000 | |
| ШС и замкнутые ЛС | Стали и сплавы | 0,15-0,35 | 1,15 | 1,2 | 1,25 | 1,3 |
| 0,05 | — | 1,25 | 1,35 | 1,4 | ||
| Разрезные ЛС | Эл. тех. стали | 0,15-0,35 | 1,3 | 1,4 | 1,5 | 1,6 |
| 0,05 | — | 1,5 | 1,6 | 1,7 | ||
| 50Н, 33НКМС | 0,05-0,1 | — | 1,7 | 1,8 | 1,9 | |
| 80НХС, 79НМ | 0,05-0,1 | — | 2,5 | 2,8 | 3 | |
Значение коэффициента добавочных потерь kp даны для сердечников средних размеров (несколько десятков Вт). Для сердечников меньших размеров значение данного коэффициента необходимо увеличить в 1,2 – 1,3 раза, а для больших сердечников уменьшить в 1,2 – 1,3 раза.
Как рассчитать потери мощности в обмотках трансформатора?
Потери мощности в обмотках трансформатора ∆рк напрямую зависят от их активного сопротивления Ri. Кроме того необходимо учитывать увеличение сопротивления из-за дополнительных факторов (увеличение температуры и скин-эффект). В общем случае потери мощности в обмотках определяются следующим выражением
где N – количество вторичных обмоток,
рki – потери в i-й обмотке,
Ii – сила тока в i-й обмотке,
Ri – сопротивление i-й обмотки.
Сопротивление обмотки рассчитывается по известной формуле, через удельное сопротивление
где lw – средняя длина витка обмотки, см,
w – число витков обмотки,
q – сечение проводника, мм2,
ρ – удельное сопротивление материала проводника, Ом*мм2/м.
Данное выражение достаточно неудобно использовать на практике. Чаще всего известны размеры сердечника, а также его основные параметры (площади и объёмы). Поэтому можно использовать следующее выражение для потерь мощности в обмотках трансформатора
где koki – коэффициент заполнения окна для i-й обмотки,
Vki – геометрический объем, занятый i-й обмоткой, см3,
ji – плотность тока для i-й обмотки, а/мм2,
Soki – площадь сечения i-й обмотки, мм2,
Если параметры ρ, j, kok одинаковы для всех обмоток либо взяты их средние значения, то получим следующее выражение
где Vk – геометрический объем, занятый всей катушкой, см3.
Как уже было сказано, при работе трансформатор нагревается. Вместе с этим изменяется активное сопротивление обмоток. Рассчитать удельное сопротивление проводника при увеличении температуры можно по следующим выражениям
где kτ — коэффициент учитывающий увеличение сопротивления из-за роста температуры,
ρ20 – удельное сопротивление проводника при температуре 20°С,
αρ – температурный коэффициент сопротивления, для меди и алюминия αρ = 0,004 1/°С,
tp – рабочая температура трансформатора, °С.
Так как в большинстве случаев в справочниках указывают удельное сопротивление материалов при температуре 20°С, то выражение можно упростить
где τ – перегрев трансформатора.
Влияние температуры на сопротивление обмотки трансформатора необходимо всегда учитывать при расчете падения напряжения на них.
Потери электроэнергии в конденсаторной установке
Источники реактивной мощности могут быть двух типов: статические КУ, к которым относятся БСК и СТК, и вращающиеся КУ – синхронные машины, к которым относятся СК и синхронные двигатели (СД).
Удельные потери мощности в БК не превышают 3 кВт/Мвар. Потери в СТК зависят от их конструкции (соотношения мощностей конденсаторов и реакторов) и в среднем составляют 6 кВт/Мвар. Потери мощности в синхронных машинах тоже зависят от конструкции машины, напряжения и скорости вращения. Их определяют по формуле
Синхронные двигатели устанавливают исходя из требований технологических процессов, поэтому рассматривается не целесообразность их установки, а целесообразность их дополнительного использования в качестве КУ. Генерируя реактивную мощность, они потребляют дополнительную активную мощность, поэтому при оценке суммарного снижения потерь в сети и СД это необходимо это учитывать. Потери холостого хода в СД в отличие от СК при этом не учитываются, так как они происходят и при неиспользовании реактивной мощности СД.
Значения D1 и D2 для большинства СД, эксплуатируемых в сетях потребителей электроэнергии, приведены в [23]. Потери в СД зависят не только от D1 и D2 , но и от напряжения на вводе СД и других параметров режима, которые не остаются постоянными в процессе работы. В оценочных расчетах потери в СД при его полной загрузке по реактивной мощности (βQ = 1) можно определять по формуле
Практически все СД изготавливаются с номинальным cos ϕ = 0,9 (tg ϕ = 0,5), поэтому их максимальная располагаемая реактивная мощность составляет половину номинальной мощности СД. Удельные потери в СД ∆pсд, кВт/Мвар, при максимальной реактивной мощности определяют по формуле
При снижении загрузки СД по реактивной мощности (βQ < 1) удельные потери снижаются и составляют (1 + βQ ) / 2 от номинальных потерь.
Коэффициенты aсд и bсд приведены в табл. 7.1. Там же для сравнения приведены вычисленные по формуле (7.39) удельные потери в СД мощностью 1 и 5 МВт.
Таблица 7.1
Коэффициенты потерь мощности в СД
Из данных табл. 7.1 следует, что удельные потери ниже в СД с большим числом оборотов и большой мощностью. Для лучших СД с точки зрения использования их реактивной мощности удельные потери составляют 8 кВт/Мвар, а для худших – 35 кВт/Мвар, что в 3– 12 раз больше потерь в БСК.
Синхронные компенсаторы применяют специально для компенсации реактивной мощности, поэтому удельные потери в них определяют с учетом потерь холостого хода. Их значения колеблются от 30 кВт/Мвар для СК мощностью 5 Мвар до 12 кВт/Мвар для СК мощностью 320 Мвар. Еще большие потери происходят при использовании в качестве СК генераторов действующих станций, не используемых в какой-то период по основному назначению или генераторов выведенных из обычной эксплуатации неэкономичных станций. Потери в СК рассмотрены в п. 2.2.2.
По удельным потерям СК существенно проигрывают конденсаторным установкам. Однако следует помнить, что установка СК производится не только с целью снижения потерь, а и (в первую очередь) с целью повышения устойчивости режимов работы энергосистем. Свойства электрических машин таковы, что при резком снижении напряжения они резко увеличивают выдаваемую реактивную мощность, поддерживая режим. Конденсаторы ведут себя прямо противоположно: при снижении напряжения их мощность снижается пропорционально квадрату напряжения в точке их подключения, усугубляя дефицит реактивной мощности.