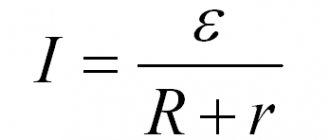Привет, мой друг, тебе интересно узнать все про метод кирхгофа, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое метод кирхгофа,закон кирхгофа , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Правила сформулированы в 1845 году, это не единственное открытие Кирхгофа. Кирхгоф и Бунзен активно изучали спектры излучения химических элементов, используя изобретения Фраунгофера. При помощи призмы или дифракционной решетки свет раскладывался на спектральные составляющие, и ученые наблюдали эффект. Так установлены индивидуальные частоты ряда элементов таблицы Менделеева. Указанные ученые заложили основы спектроскопии. Кирхгоф массу времени посвятил разным отраслям науки. К примеру, нашел ошибку в постановке граничных условий для решения дифференциальных уравнений по колебаниям мембран, представленных на суд публики в 1811 году Софи Жермен. Не нужно думать, что словосочетание закон кирхгофа узко ограничено двумя правилами, причем одно прямо приводит к сформулированному ранее закону Ома.
| нем. Gustav Robert Kirchhoff | |
| Дата рождения | 12 марта 1824 |
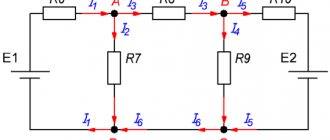
Пример сложной электрической цепи вы можете посмотреть на рисунке 1.
Рисунок 1. Сложная электрическая цепь .
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
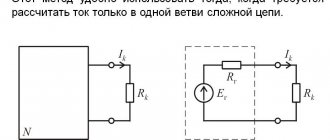
Самый точный метод, но с его помощью можно определять параметры схемы с небольшим количеством контуров (1-3). Алгоритм: 1. Определить количество узлов q, ветвей p и независимых контуров; 2. Задаться направлениями токов и обходов контуров произвольно; 3. Установить число независимых уравнений по 1-ому закону Кирхгофа (q — 1) и составить их, где q-количество узлов; 4. Определить число уравнений по 2-ому закону Кирхгофа (p – q + 1) и составить их; 5. Решая совместно уравнения, определяем недостающие параметры цепи; 6. По полученным данным производится проверка расчетов, подставляя значения в уравнения по 1-ому и 2-ому законам Кирхгофа или составив и рассчитав баланс мощностей . Пример:
Рис 1. Согласно предложенному алгоритму, определим количество узлов и ветвей схемы рис. 1 q = 3, p = 5, следовательно, уравнений по 1-ому закону Кирхгофа равно 2, а уравнений по 2-ому закону Кирхгофа равно 3. Запишем эти уравнения согласно правилам:
Составим уравнения баланса мощностей:
Правила и законы Кирхго́фа
Правила Кирхгофа (часто в технической литературе называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока.
Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчетов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году.
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с еще двумя законами Кирхгофа в химии и физике.
Метод контурных токов
Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже
Расчет цепи методом контурных токов.
Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.
В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях
Остальные же токи можно найти как разность двух контурных токов
В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа
Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений
В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Онлайн демонстрация и симуляция работы метод кирхгофа: Открыть на весь экран
Поясним первый закон Кирхгофа на примере рисунка 2.
Рисунок 2. Узел электрической цепи.
Здесь ток I1— ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
I1 = I2 + I3 (1)
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим:
I1 — I2 — I3 = 0 (2)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Расчёт электрических цепей онлайн
На сайте появилась программа для расчёта установившихся режимов электрических цепей по законам ТОЭ. На настоящий момент реализованы методы расчёта по законам Ома, по законам Кирхгофа, по методу узловых потенциалов, методу контурных токов, методу эквивалентного генератора. Также программа позволяет рассчитать эквивалентное сопротивление цепи относительно источника питания. Программа позволяет нарисовать схему, задать параметры её элементов и рассчитать схему. В результате формируется текстовое описание порядка расчёта, рассчитывается баланс мощностей и строятся векторные диаграммы.
Рисование схемы производится путём перетаскивания элементов методом drag-and-drop из боковой панели и последующим соединением выбранных элементов.
В боковой панели доступны следующие элементы с задаваемыми параметрами:
- резистор : номер элемента;
- сопротивление, Ом;
- номер элемента;
- номер элемента;
- номер элемента;
- номер элемента;
Инструкция по применению программы приведена здесь.
Методы расчёта
После завершения рисования схемы при нажатии кнопки «Расчёт» запускается расчёт электрической цепи. Программа анализирует исходную схему и при выявлении каких-либо ошибок сообщает об этом. При успешном анализе схемы запускается расчёт по методам ТОЭ.
Расчёт по закону Ома
Расчёт по закону Ома осуществляется для одноконтурных схем. Используемая методика расчёта приведена здесь.
Пример схемы и расчёт:
Исходные данные и схема:
- E1: Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
- Номер элемента: 1
После нажатия кнопки «Расчёт» формируется решение:
В исходной схеме только один контур. Рассчитаем её по закону Ома.
Согласно закону Ома, ток в замкнутой цепи равен отношению ЭДС цепи к сопротивлению. Составим уравнение, приняв за положительное направление тока $ \underline{I} $ направление источника ЭДС $ \underline{E}_{1} $:
$$ R_{1}\cdot \underline{I} = \underline{E}_{1} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ 1.0\cdot \underline{I}=100 $$
Отсюда искомый ток в цепи равен
$$ \underline{I} = 100\space \textrm{А}$$
Расчёт по законам Кирхгофа
Для многоконтурных схем расчёт осуществляется по законам Кирхгофа. Используемая методика расчёта приведена здесь.
Пример схемы и расчёт:
Исходные данные и схема:
- E1: Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
- Номер элемента: 1
- Номер элемента: 1
- Номер элемента: 1
После нажатия кнопки «Расчёт» на исходной схеме появляется нумерация узлов и формируется решение:
Рассчитаем схему по законам Кирхгофа.
В данной схеме: узлов − 2 , ветвей − 3, независимых контуров − 2.
Произвольно зададим направления токов в ветвях и направления обхода контуров.
Принятые направления токов: Ток $ \underline{I}_{1} $ направлен от узла ‘2 у.’ к узлу ‘1 у.’ через элементы $ \underline{E}_{1} $, $ R_{1} $. Ток $ \underline{I}_{2} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ L_{1} $. Ток $ \underline{I}_{3} $ направлен от узла ‘1 у.’ к узлу ‘2 у.’ через элементы $ C_{1} $.
Принятые направления обхода контуров: Контур №1 обходится через элементы $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ в указанном порядке. Контур №2 обходится через элементы $ L_{1} $, $ C_{1} $ в указанном порядке.
Составим уравнения по первому закону Кирхгофа. При составлении уравнений «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» − со знаком «−».
Количество уравнений, составляемых по первому закону Кирхгофа, равно $ N_\textrm{у} − 1 $, где $ N_\textrm{у} $ − число узлов. Для данной схемы количество уравнений по первому закону Кирхгофа равно 2 − 1 = 1.
Составим уравнение для узла №1:
$$ \underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3} = 0 $$
Составим уравнения по второму закону Кирхгофа. При составлении уравнений положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура.
Количество уравнений, составляемых по второму закону Кирхгофа, равно $ N_\textrm{в} − N_\textrm{у} + 1 $, где $ N_\textrm{в} $ — число ветвей. Для данной схемы количество уравнений по второму закону Кирхгофа равно 3 − 2 + 1 = 2.
Составим уравнение для контура №1:
$$ R_{1}\cdot \underline{I}_{1} + jX_{L1}\cdot \underline{I}_{2}=\underline{E}_{1} $$
Составим уравнение для контура №2:
$$ jX_{L1}\cdot \underline{I}_{2} − (−jX_{C1})\cdot \underline{I}_{3}=0 $$
Объединим полученные уравнения в одну систему, при этом перенесём известные величины в правую сторону, оставив в левой стороне только составляющие с искомыми токами. Система уравнений по законам Кирхгофа для исходной цепи выглядит следующим образом:
$$ \begin{cases}\underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3} = 0 \\ R_{1}\cdot \underline{I}_{1}+jX_{L1}\cdot \underline{I}_{2} = \underline{E}_{1} \\ jX_{L1}\cdot \underline{I}_{2}−(−jX_{C1})\cdot \underline{I}_{3} = 0 \\ \end{cases} $$
Подставим в полученную систему уравнений значения сопротивлений и источников и получим:
$$ \begin{cases}\underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3}=0 \\ \underline{I}_{1}+ j \cdot \underline{I}_{2}=100 \\ j \cdot \underline{I}_{2}+ j \cdot \underline{I}_{3}=0 \\ \end{cases} $$
Решим систему уравнений и получим искомые токи:
$$ \underline{I}_{1} = 0 $$
$$ \underline{I}_{2} = −100j $$
$$ \underline{I}_{3} = 100j $$
Рекомендуемые записи
- Расчёт электрических цепей по методу узловых потенциалов: вывод метода
Наряду с решением электрических схем по законам Кирхгофа и методом контурных токов используется метод узловых… - Законы Кирхгофа для расчёта электрических цепей При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие…
- Векторные диаграммы электрических цепей При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной…
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Онлайн демонстрация и симуляция работы метод кирхгофа: Открыть на весь экран
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.
Рисунок 3 . Об этом говорит сайт https://intellect.icu . Электрическая цепь, для пояснения второго закона Кирхгофа.
E1- Е2 = -UR1 — UR2 или E1 = Е2 — UR1 — UR2 (3)
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
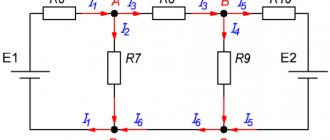
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Рис. 1. Схема контура
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Рис. 2. Абстрактный узел
Запишем наши выводы в алгебраической форме, для общего случая:
Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
О значении для электротехники
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приемами и способами ( метод эквивалентного генератора , принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Закон излучения Кирхгофа
Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.
В современной формулировке закон звучит следующим образом:
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Известно, что при падении электромагнитного излучения на некоторое тело часть его отражается, часть поглощается и часть может пропускаться. Доля поглощаемого излучения на данной частоте называется поглощательной способностью тела . С другой стороны, каждое нагретое тело излучает энергию по некоторому закону, именуемому излучательной способностью тела .
Величины и могут сильно меняться при переходе от одного тела к другому, однако, согласно закону излучения Кирхгофа, отношение испускательной и поглощательной способностей не зависит от природы тела и является универсальной функцией частоты (длины волны) и температуры:
По определению, абсолютно черное тело поглощает все падающее на него излучение, то есть для него . Поэтому функция совпадает с излучательной способностью абсолютно черного тела, описываемой формулой Планка, вследствие чего излучательная способность любого тела может быть найдена, исходя лишь из его поглощательной способности.
Реальные тела имеют поглощательную способность меньше единицы, а значит, и меньшую, чем у абсолютно черного тела, излучательную способность. Тела, поглощательная способность которых не зависит от частоты, называются серыми. Их спектр имеет такой же вид, как и у абсолютно черного тела. В общем же случае поглощательная способность тел зависит от частоты и температуры, и их спектр может существенно отличаться от спектра абсолютно черного тела. Изучение излучательной способности разных поверхностей впервые было проведено шотландским ученым Лесли при помощи его же изобретения — куба Лесли.
В теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты . В экспериментальных работах удобнее пользоваться функцией длины волны . Обе функции связаны друг с другом формулой
В астрофизике закон Кирхгофа часто применяется в следующем виде:
,
где — коэффициент излучения (энергия, излучаемая единичным объемом в единичном интервале частот в единичный телесный угол за единицу времени); — коэффициент поглощения с учетом вынужденного испускания (, где — плотность вещества, а и — соответственно непрозрачность и эффективная длина пробега фотонов для частоты ); — интенсивность излучения абсолютно черного тела.
Закон Кирхгофа справедлив только для случаев теплового равновесия. Однако, его часто применяют и для неравновесных систем, когда излучение не находится в равновесии с веществом и его распределение по частотам существенно отличается от планковского. При этом часто (но не всегда) предположение о термодинамическом равновесии между частицами излучающего вещества оказывается хорошим приближением. Степень отклонения от закона Кирхгофа может служить мерой отличия излучения космических объектов от теплового.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
Рис. 4. Магнитные контуры цепей
В частности: ∑Ф=0.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Закон Кирхгофа в химии
Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе реакции.
Дифференциальная форма закона:
Интегральная форма закона:
где и — изобарная и изохорная теплоемкости, — разность изобарных теплоемкостей продуктов реакции и исходных веществ, — разность изохорных теплоемкостей продуктов реакции и исходных веществ, а и — соответствующие тепловые эффекты.
Если разница невелика, то можно принять и , соответственно интегральная форма уравнений примет следующий вид:
При большой разнице температур необходимо учитывать температурные зависимости теплоемкостей: и
См. также
- метод двух узлов ,
- анализ цепей синусоидального тока , закон ома в комплексной форме ,
- метод двух узлов ,
- теорема тевенена ,
- теорема нортона ,
- закон ома для участка цепи , закон ома ,
Тебе нравиться метод кирхгофа? илиу тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое метод кирхгофа,закон кирхгофа и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
1.10. Правила Кирхгофа для разветвленных цепей
Для упрощения расчетов сложных электрических цепей, содержащих неоднородные участки, используются правила Кирхгофа, которые являются обобщением закона Ома на случай разветвленных цепей.
В разветвленных цепях можно выделить узловые точки (узлы), в которых сходятся не менее трех проводников (рис. 1.10.1). Токи, втекающие в узел, принято считать положительными; вытекающие из узла – отрицательными.
| Рисунок 1.10.1. Узел электрической цепи. I1, I2 > 0; I3, I4 <� 0 |
В узлах цепи постоянного тока не может происходить накопление зарядов. Отсюда следует первое правило Кирхгофа:
Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю:
| I1 + I2 + I3 + … + In = 0. |
Первое правило Кирхгофа является следствием закона сохранения электрического заряда.
В разветвленной цепи всегда можно выделить некоторое количество замкнутых путей, состоящих из однородных и неоднородных участков. Такие замкнутые пути называются контурами. На разных участках выделенного контура могут протекать различные токи. На рис. 1.10.2 представлен простой пример разветвленной цепи. Цепь содержит два узла a и d, в которых сходятся одинаковые токи; поэтому только один из узлов является независимым (a или d).
| Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef) |
В цепи можно выделить три контура abcd, adef и abcdef. Из них только два являются независимыми (например, abcd и adef), так как третий не содержит никаких новых участков.
Второе правило Кирхгофа является следствием обобщенного закона Ома.
Запишем обобщенный закон Ома для участков, составляющих один из контуров цепи, изображенной на рис. 1.10.2, например, abcd. Для этого на каждом участке нужно задать положительное направление тока и положительное направление обхода контура. При записи обобщенного закона Ома для каждого из участков необходимо соблюдать определенные «правила знаков», которые поясняются на рис. 1.10.3.
| Рисунок 1.10.3. «Правила знаков» |
Для участков контура abcd обобщенный закон Ома записывается в виде:
Для участка bc: I1R1 = Δφbc – 1.
Для участка da: I2R2 = Δφda – 2.
Складывая левые и правые части этих равенств и принимая во внимание, что Δφbc = – Δφda , получим:
| I1R1 + I2R2 = Δφbc + Δφda – 1 + 2 = –1 – 2. |
Аналогично, для контура adef можно записать:
| – I2R2 + I3R3 = 2 + 3. |
Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.
Первое и второе правила Кирхгофа, записанные для всех независимых узлов и контуров разветвленной цепи, дают в совокупности необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов в электрической цепи. Для цепи, изображенной на рис. 1.10.2, система уравнений для определения трех неизвестных токов I1, I2 и I3 имеет вид:
| I1R1 + I2R2 = – 1 – 2, |
| – I2R2 + I3R3 = 2 + 3, |
| – I1 + I2 + I3 = 0. |
Таким образом, правила Кирхгофа сводят расчет разветвленной электрической цепи к решению системы линейных алгебраических уравнений. Это решение не вызывает принципиальных затруднений, однако, бывает весьма громоздким даже в случае достаточно простых цепей. Если в результате решения сила тока на каком-то участке оказывается отрицательной, то это означает, что ток на этом участке идет в направлении, противоположном выбранному положительному направлению.
| Модель. Цепи постоянного тока |
| Модель. Конденсаторы в цепях постоянного тока |