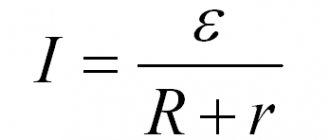В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта https://www.sxemotehnika.ru.
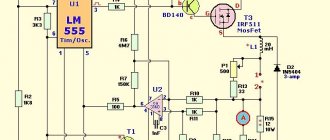
Пример сложной электрической цепи вы можете посмотреть на рисунке 1.
Рисунок 1. Сложная электрическая цепь.
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
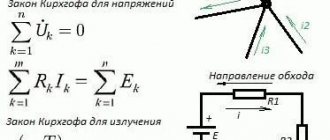
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.
Рисунок 2. Узел электрической цепи.
Здесь ток I1— ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
I1 = I2 + I3 (1)
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим:
I1 — I2 — I3 = 0 (2)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
О значении для электротехники
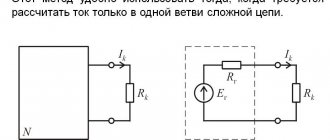
Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приемами и способами ( метод эквивалентного генератора , принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
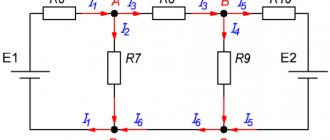
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.
Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
E1- Е2 = -UR1 — UR2 или E1 = Е2 — UR1 — UR2 (3)
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Правила и законы Кирхго́фа
Правила Кирхгофа (часто в технической литературе называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.
Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока.
Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчетов сложных электрических цепей.
Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.
Сформулированы Густавом Кирхгофом в 1845 году.
Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с еще двумя законами Кирхгофа в химии и физике.
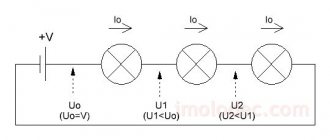
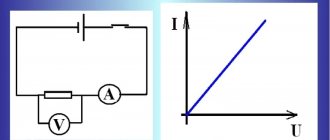
Применим на практике закон Ома
Проверим на практике, действительно ли «работает» закон Ома. Возьмем батарейку или аккумулятор напряжением около 9 вольт. Нам нужно узнать, какой ток будет протекать, если мы замкнем цепь, подключив к ней резистор 10 кОм. Кружок с надписью «mA» на схеме обозначает наш мультиметр (тестер), настроенный на измерение амперов.
Вначале проверяем теоретически. Для этого используем известные нам формулы:
U = 9 В, R = 10 кОм , I =?
I = U / R = 9 В / 10000 Ом = 0,0009 A = 0,9 мА
Значит тестер нам должен показать около 0,9 мА . Теперь соберите данную схему на макетной плате. В случае возникновения проблем вы можете использовать пример ниже. Просто будьте осторожны, чтобы не допустить короткого замыкания в цепи при установке компонентов, при замыкании можно повредить аккумулятор.
| Не забудьте правильно настроить мультиметр при измерении тока! |
Результат измерения в указанной выше цепи составляет 0,95 мА . Почему по расчетам у нас получилась одна цифра, а на практике, после измерения тестером, другая? Не следует забывать, что измерения имеют погрешность. Как вы помните, из предыдущей статьи, все резисторы имеют погрешность около 5%, также, сопротивление щупов и самого мультиметра, и к тому же, батарея или аккумулятор может быть не заражена на все 9В! В среднем получается, что результат верный!
Теперь, для теста, нам нужно проверить, что произойдет, если мы подключим другой резистор, а именно 1 кОм , вместо резистора 10 кОм. Держа в голове закон Ома, мы уже должны предугадать, что подключение резистора с в 10 раз меньшим сопротивлением должно давать в 10 раз больший ток. Проверим:
Читать также: Как сделать автоматическое включение света?
Потенциометр — проверяем на практике
Вставьте потенциометр в макетную плату и измерьте сопротивление между центральным выводом и любым другим выводом. После поворота белой ручки (головки) потенциометра сопротивление должно измениться.
| Измерения сопротивления потенциометра до поворота ручки. | Измерения сопротивления потенциометра после поворота ручки. |
Теперь проверим, как потенциометр работает, т.е. делит напряжение. Подключите питание аккумулятора к крайним контактам (ножкам) элемента (полярность не имеет значения), а затем измерьте напряжение между средним контактом и любым крайним контактом. Не забудьте правильно настроить мультиметр. Через некоторое время поворачиваем белую головку (ручку) потенциометра и делаем второе измерение. Полученные результаты могут выглядеть так:
Читать также: Что такое процессор ARM?
| Измерение напряжения на потенциометре. | Повторное измерение напряжения. |
См. также
- метод двух узлов ,
- анализ цепей синусоидального тока , закон ома в комплексной форме ,
- метод двух узлов ,
- теорема тевенена ,
- теорема нортона ,
- закон ома для участка цепи , закон ома ,
Тебе нравиться метод кирхгофа? илиу тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое метод кирхгофа,закон кирхгофа и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Как работают интегральные схемы стабилизации напряжения?
Наш эксперимент показал, что напряжение источника питания зависит от тока, потребляемого системой. Если потребляемый ток относительно высок, напряжение батареи может значительно упасть. Так как же работают интегральные схемы стабилизации питания, обеспечивающие стабильное значение напряжения независимо от нагрузки?
В случае интегральных схем стабилизации питания ситуация несколько иная: встроенная в них стабилизирующая схема постоянно сравнивает напряжение на выводах с напряжением, запрашиваемым пользователем, и «регулирует» его, если оно слишком низкое. Следовательно, внутреннее сопротивление таких источников питания может быть во много раз ниже, чем у даже больших батарей.
Что такое потенциометры?
Потенциометры представляют собой резисторы с регулируемым значением сопротивления. Поворачивая ручку потенциометра, мы влияем на его сопротивление, измеряемое между средним и крайним выводом. Примеры потенциометров:
Потенциометры на схемах представлены двумя способами (символ не имеет отношения к типу элемента):
В зависимости от исполнения корпуса, выводы или ножки могут быть расположены по-разному, но всегда легко выделить средний вывод, который является наиболее важным:
Потенциометры — это очень умные делители напряжения: ротор, из хорошо проводящего материала, движется по резестивному веществу с постоянным сопротивлением, разделяя его на два резистора. Поэтому схема потенциометра выглядит так:
Внутри, потенциометр выглядит примерно так, как показано ниже — резисторы, отмеченные красным, являются лишь символическим представлением того факта, что ротор делит резестивное вещество с постоянным сопротивлением на две части (одна, крайняя ножка + середина, а другая, крайняя + середина) .
Сумма сопротивлений двух резисторов, полученная таким образом, является постоянной, но величина резистора, на который подается напряжение, изменяется. Сопротивление между крайними выводами постоянно, средний вывод нашего резистора — переменное сопротивление.
Для облегчения понимания показан современный потенциометр в разборе:
Кроме того, потенциометр можно использовать как резистор с регулируемым сопротивлением — достаточно использовать один из крайних выводов и ручку. Теперь проверим теорию на практике.
Закон Ома
Ток, напряжение и сопротивление связаны напрямую с законом Ома, описывающим отношение напряжения (приложенного к элементу) к заданному сопротивлению, в результате которого протекает ток.
| Помните, что мы всегда обозначаем эти значения следующим образом: U — напряжение, R — сопротивление, I — ток. |
Вы очень часто придется встречаться с этим законом в области электроники. К счастью, вам не нужно учить этот закон наизусть, т.к. в простейшей форме оно выражается тремя простыми формулами, которые для удобства использования обычно записываются в виде треугольника, как на картинке ниже:
| На самом деле это один паттерн (шаблон), трансформируется по мере необходимости. Достаточно запомнить одну из формул (например, U = I * R), чтобы в любой момент преобразовать ее в другую. |
Зачем нужен делитель напряжения?
В мире электроники популярны датчики, с помощью которых, измеряемые физические значения, считываются путем измерения сопротивления датчика, например, сопротивление аналогового датчика температуры зависит от температуры окружающей среды.
Микроконтроллеры (например, используемые в Arduino) не могут измерять изменения сопротивления. Однако они отлично умеют измерять напряжение.
На сегодняшний день такие делители напряжения в электросхемах не используются. Вы конечно можете использовать такой делитель для питания системы, которая требует 5 В от батареи 9 В. Но вы не должны использовать их для питания, например, средних моторов (хотя это иногда и кажется хорошей идеей), ведь от делителей напряжения невозможно получить большую силу тока! Для питания таких схем с моторами лучше использовать стабилизаторы напряжения, о которых будет рассказано в других статьях.
Постоянный ток
Прочитав статейки про первый и второй законы Кирхгофа, уважаемый читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»
Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!
Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.
Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа. Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.
Рисунок 1 – Простая схема
В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа. В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.
Господа, хочу отметить один тонкий момент. Хоть контура и три, независимых из них только два. Третий контур включает в себя все остальные и не может считаться независимым. И вообще всегда при всех расчетах мы должны использовать только независимые контура. Не поддавайтесь искушению записать еще одно уравнение за счет этого общего контура, ничего хорошего не выйдет .
Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.
Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I1, I2, I3.
Мы видим, что в контуре №1 направление токов I1 и I3, а также направление источника питания совпадают с направлением обхода, поэтому будем считать их со знаком плюс. В контуре №2 ток I2 совпадет с направлением обхода, поэтому будет со знаком плюс, а ток I3 направлен в другую сторону, поэтому будет со знаком минус. Запишем второй закон Кирхгофа для контура №1:
А теперь запишем этот же закон для контура №2:
Видим, что в контуре №2 нет источников питания, поэтому в левой части (где у нас согласно второму закону Кирхгофа стоит сумма ЭДС) у нас нолик. Итак, у нас есть два уравнения, а неизвестных-то у нас три (I1, I2, I3). А нам известно, что для нахождения трех неизвестных нужна система с тремя независимыми уравнениями. Где же взять третье недостающее уравнение? А, например, из первого закона Кирхгофа! Согласно этому закону мы можем записать
Господа, теперь полный порядок, у нас есть три уравнения и три неизвестных и нам остается только решить вот такую вот систему уравнений
Подставим конкретные числа. Все расчеты будем вести в кошерной системе СИ. Рекомендую всегда считать только в ней. Не поддавайтесь искушению подставлять куда-то миллиметры, мили, килоамперы и прочее. Возможно возникновение путаницы.
Решение таких систем рассматривается чуть ли не в начальной школе и, полагаю, не должно вызывать трудностей . Если что, есть куча математических пакетов, которые сделают это за вас, если вам лень самим ручками считай. Поэтому мы опустим процесс решения, а сразу приведем результат
Видим, что все токи получились у нас со знаком плюс. Это значит, что мы верно угадали их направление. Да, то есть токи в схеме текут именно в том направлении, как мы нарисовали стрелочки на рисунке 1. Однако из условия задачи необходимо найти не только токи через резисторы, но и падение напряжения на них. Как это сделать? Например, с помощью уже изученного нами закона Ома. Как мы помним, закон Ома связывает между собой ток, напряжение и сопротивление. Если нам известны любые две из этих величин, мы легко можем найти третью. В данном случае мы знаем сопротивление и ток, который течет через это сопротивление. Поэтому, используя вот эту формулу
находим напряжение на каждом резисторе
Заметим, господа, что напряжения на резисторах R2 и R3 равны между собой. Это и логично, поскольку они соединены между собой параллельно. Однако пока не будем на этом акцентировать большое внимание, рассмотрим это лучше в другой раз.
Итак, господа, мы решили эту простую задачку с помощью двух законов Кирхгофа и закона Ома. Но это был совсем простой пример. Давайте попробуем решить более сложную задачу. Взгляните на рисунок 2.
Рисунок 2 – Схема посложнее
Схема выглядит внушительно, не правда ли? Возможно, вам даже не верится, что эту схему можно легко рассчитать. Однако, господа, уверяю вас, вы обладаете всеми необходимыми знаниями для расчета этой схемы, если уже изучили мои предыдущие статьи. Сейчас вы в этом убедитесь.
Для начала зададимся конкретными цифрами значений сопротивлений резисторов и напряжений источников.
Пусть Е1=15 В, Е2=24 В, R1= 10 Ом, R2 = 51 Ом, R3=100 Ом, R4=1 кОм, R5=10 Ом, R6=18 Ом, R7=10 кОм.
Найти, как и в прошлой задаче, требуется все токи в схеме и напряжения на всех резисторах.
В этой схеме мы можем видеть три независимых контура. Обозначим их римскими цифрами I, II, III. В каждом контуре зададимся направлением обхода. Они показаны синими стрелками.
Дальше как и в прошлый раз наугад расставим направления токов во всех ветвях и подпишем где какой ток. Видно, что всего у нас 6 ветвей и, соответственно, 6 разных токов (I1…I6).
Теперь запишем второй закон Кирхгофа для всех трех независимых контуров.
Второй закон Кирхгофа для контура I:
Второй закон Кирхгофа для контура II:
Второй закон Кирхгофа для контура III:
У нас есть три уравнения, однако неизвестных токов аж 6. Как и в прошлой задаче для получения недостающих уравнений запишем первые законы Кирхгофа для узлов.
Первый закон Кирхгофа для узла А:
Первый закон Кирхгофа для узла В:
Первый закон Кирхгофа для узла С:
Собственно, у нас теперь есть система из 6 уравнений с 6 неизвестными. Остается только решить эту систему
Подставляя числа, заданные в условии, получаем
Опуская решения за пределами статьи, приведем итоговый результат
Господа, мы видим, что почти все токи, кроме I4 получились у нас со знаками «минус». Это значит, что мы не угадали их направление, когда рисовали стрелочки на рисунке 2 . То есть все токи, кроме тока I4 на самом деле текут в противоположные стороны. А ток I4 течет так, как мы нарисовали. Хотя бы с ним мы угадали верно.
Теперь все по тому же закону Ома ровно как в прошлом примере рассчитаем напряжения на резисторах:
Вот и все, господа: схема рассчитана, а задачка решена. Таким образом, вы теперь обладаете весьма мощным инструментом по расчету электрических схем. С помощью двух законов Кирхгофа и закона Ома вы сможете рассчитать весьма непростые схемы, найти величины токов и их направления, а также напряжения на всех нагрузках цепи. Более того, зная токи и напряжения вы легко сможете рассчитать и мощности, которые на этих резисторах выделяются, если воспользуетесь рекомендациями из моей предыдущей статьи.
На этом на сегодня все господа. Огромной вам всем удачи и успешных расчетов!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla