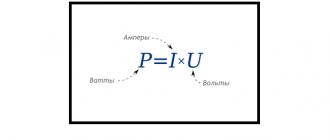
Задачи по теме «сила Лоренца»
Даже если вы не новичок, прежде чем решать задачи, прочтите общую памятку и на всякий случай держите под рукой полезные формулы.
Задача на силу Лоренца №1
Условие
Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.
Решение
Скорость электрона можно найти из формулы кинетической энергии:
E к = m · v 2 2 v = 2 E к m
Сила Лоренца является центростремительной силой, значит, по второму закону Ньютона, можно записать:
Магнитная индукция равна напряженности, умноженной на магнитную постоянную. Подставив ранее найденное выражение для скорости в формулу для радиуса и силы Лоренца, запишем:
R = m 2 E к т q μ 0 H = 2 E к т q μ 0 H F л = q 2 E к т μ 0 H
Теперь осталось только подставить значения и вычислить:
v = 2 · 4 , 8 · 10 — 16 9 , 1 · 10 — 31 = 3 , 25 · 10 7 м с F л = 4 · 3 , 14 · 10 — 7 · 465 · 1 , 6 · 10 — 19 · 3 , 25 · 10 7 = 3 · 10 — 15 Н R = 2 · 4 , 8 · 10 — 16 · 9 , 1 · 10 — 31 4 · 3 , 14 · 10 — 7 · 465 · 1 , 6 · 10 — 19 = 0 , 32 м
Ответ: v = 3 , 25 · 10 7 м с ; F л = 3 · 10 — 15 Н ; R = 0 , 32 м .
Задача на силу Лоренца №2
Условие
Альфа-частица влетает в магнитное поле с индукцией 1 Тл перпендинулярно силовым линиям. Найти момент импульса частицы относительно центра окружности, по которой она будет двигаться.
Решение
Когда частица влетает в поле перпендикулярно силовым линиям, на нее начинает действовать сила Лоренца, которая выполняет роль центростремительной силы. Радиус окружности, по которой будет двигаться частица:
R = m v Q B m = 6 , 65 · 10 — 27 к г — м а с с а а л ь ф а ч а с т и ц ы Q = 2 e = 3 , 2 · 10 — 19 К л — з а р я д а л ь ф а ч а с т и ц ы
Момент импульса частицы относительно центра окружности найдем по формуле:
L = m v R = m 2 v 2 Q B = 6 , 65 · 10 — 27 2 · 0 , 35 · 10 7 2 3 , 2 · 10 — 19 · 1 = 5 , 42 · 10 — 21 к г · м 2 с
Ответ: 5 , 42 · 10 — 21 к г · м 2 с .
Задача на силу Лоренца №3
Условие
В однородном магнитном поле с индукцией В = 0,5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определите разность потенциалов U на концах стержня.
Решение
Рассмотрим физическую суть процессов, проходящих в стержне. Когда стержень движется в магнитном поле, в нем возникает ЭДС индукции, которая обусловлена действием силы Лоренца на заряды стержня.
Под действием этой силы в стержне происходит разделение зарядов: свободные электроны перемещаются вверх и между концами стержня возникает разность потенциалов.
Заряды на концах стержня создают поле E, препятствующее дальнейшему разделению зарядов. В какой-то момент сила Лоренца уравновесится с силой возникающего поля:
F л = e · Е Е = F л е = e v B e = v B
Скорость нижнего конца стержня, а значит, и скорость электронов в нем, можно найти, зная частоту вращения и длину стержня:
v = 2 π · n · l
C учетом этого, перепишется выражения для напряженности электрического поля:
Е = 2 π n l B
Индуцируемая разность потенциалов, по определению, равна:
U = Е · l U = 2 π n l 2 B = 2 · 3 , 14 · 10 — 1 · 0 , 2 2 · 0 , 5 = 1 , 3 В
Ответ: 1,3 В.
Задача на силу Лоренца №4
Условие
Какая сила действует на заряд 0,005 Кл, движущийся в магнитном поле с индукцие 0,5 Тл со скоростью 150 м/с под углом 45 градусов к вектору магнитной индукции?
Решение
Это простейшая задача на определение силы Лоренца. Вспомним формулу и запишем, что на заряд действует сила Лоренца, равная:
F = q · v · B · sin α
Подставим значения и вычислим:
F = 0 , 005 · 150 · 0 , 5 · 2 2 = 0 , 26 Н
Ответ: 0,26 Н.
Задача на силу Лоренца №5
Условие
На тело с зарядом 0,8 мКл, движущееся в магнитном поле, со стороны поля действует сила, равная 32Н. Какова скорость тела, если вектор магнитного поля перпендикулярен ей?
Решение
Это классическая задача на применение формулы силы Лоренца. Так как векторы скорости и магнитной индукции перпендикулярны, можно записать:
F = q v B sin α = q v B v = F q B = 32 0 , 8 · 10 — 3 · 2 = 20 · 10 3 м с
Ответ: 20000 м/с.
Проходите магнитостатику? Вам также может быть интересно:
- Задачи на закон Био-Савара-Лапласа.
- Задачи на теорему о циркуляции магнитного поля.
Определение и формула
Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.
Рис. 1. Выводы Лоренца
Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.
По закону Ампера:
Учитывая, что
(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:
Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:
Модуль F вычисляется по формуле:
Из формулы следует:
- Сила Лоренца приобретает максимальное значение, если угол α прямой.
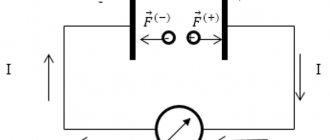
- Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
- Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).
Рис. 2. Заряженная частица между полюсами магнитов
Рис. 3. Ориентация вектора в зависимости от полярности заряда
Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).
Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.
В чём измеряется?
Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10-n Н, где 0<�К<1, а n – порядок числа 10.
Когда возникает?
Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.
Для возникновения силы Лоренца необходимо выполнить три условия:
- У частицы должен быть отрицательный или положительный заряд.
- Заряженная частица должна находиться в магнитном поле.
- Частица должна быть в движении, то есть вектор v ≠ 0.
Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера
.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки
.
Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки
.
Правило левой руки
.
Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера
.
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен . Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике, — их концентрация (число в единице объёма). Тогда:
где — объём проводника, — площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
Направление силы Лоренца
Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.
Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).
Рис. 4. Нахождение вектора силы Лоренца
Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.
Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.
Рис. 5. Пример применения правила правой руки
Магнетизм. Определения, понятия и законы
Магнитное поле. Индукция магнитного поля (магнитная индукция)
Силовое поле, действующее на движущиеся электрические заряды, электрические токи и намагниченные тела (магниты), называется магнитным полем. В свою очередь, магнитное поле создается движущимися зарядами, токами и магнитами. Силовой характеристикой магнитного поля является вектор магнитной индукции . Понятие о векторе магнитной индукции вводится на основании следующих опытных фактов: а) ориентирующее действие магнитного поля на замкнутый плоский контур (рамку) с током, б) существование силы, действующей на проводник с током в магнитном поле, в) отклонение пучка заряженных частиц в магнитном поле.
Действие магнитного поля на рамку с током
На плоскую рамку с током, подвешенную на нити в однородном магнитном поле, действует момент сил, который стремится развернуть ее определенным образом.
Рис. 3.3.1. Выбор направления вектора магнитной индукции
Ориентирующее действие поля на рамку используется для выбора направления вектора магнитной индукции. С этой целью вводят понятие положительной нормали к рамке, которая определяется как единичный вектор, перпендикулярный плоскости рамки и направленный в сторону перемещения буравчика (винта), если вращать его по направлению тока в рамке (рис. 3.3.1). За направление вектора магнитной индукции в данной точке пространства принимается направление положительной нормали к рамке, свободно устанавливающейся в магнитном поле в окрестности данной точки. Это направление совпадает с направлением от южного полюса к северному полюсу свободно вращающейся магнитной стрелки.
Замкнутый контур площадью с током создает магнитный момент
(3.3.1)
Направление магнитного момента рамки с током, свободно устанавливающейся в магнитном поле, совпадает с направлением вектора магнитной индукции.
Линии магнитной индукции
Графически магнитное поле изображают с помощью линий магнитной индукции, которые представляют собой линии, касательные к которым направлены так же, как вектор в данной точке, а густота которых пропорциональна величине поля в данной точке. В качестве примера на рис. 3.3.2 изображены линии магнитной индукции, создаваемой постоянным магнитом. Линии магнитной индукции всегда замкнуты. Представленные на рис. 3.3.2 линии замыкаются внутри магнита.
Для вычисления магнитного поля электрического тока используют формулу Био-Савара-Лапласа. Согласно этой формуле, магнитная
Рис. 3.3.2. Линии магнитной индукции, создаваемой постоянным магнитом
индукция, создаваемая отрезком проводника длиной , по которому течет ток , равна:
(3.3.2)
где — радиус-вектор, проведенный от элемента , в точку наблюдения, — угол между векторами и — магнитная проницаемость среды, — магнитная постоянная.
Картины линий индукции магнитного поля прямого тока и соленоида
Формула (3.3.2) позволяет рассчитать магнитную индукцию , созданную проводником с током любой формы. Так, величина магнитной индукции бесконечно длинного проводника с током на расстоянии от него равна
(3.3.3)
Линии магнитной индукции представляют собой концентрические окружности в плоскостях, перпендикулярных проводнику (рис. 3.3.3). Направление магнитной индукции тока определяется правилом буравчика: если поступательное движение буравчика совпадает с направлением тока, то вращение рукоятки буравчика указывает направление магнитного поля.
Магнитное поле внутри длинного соленоида (катушки с током) вдали от его концов является однородным (рис. 3.3.4). Магнитная индукция внутри соленоида в точках, удаленных от его концов, равна
(3.3.4)
где — ток, протекающий по виткам, — число витков, — длина соленоида. Магнитное поле вне соленоида подобно магнитному полю полосового постоянного магнита (ср. с рис. 3.3.2). Конец катушки, из которого выходят линии индукции, аналогичен северному полюсу магнита; другой конец аналогичен южному магнитному полюсу. Расположение полюсов катушки и направление магнитного поля
Рис. 3.3.3. Линии магнитной индукции бесконечно длинного прямого проводника с током Рис. 3.3.4. Линии магнитной индукции соленоида
определяется по правилу буравчика: если вращать рукоятку буравчика по току, то перемещение буравчика укажет направление линий магнитной индукции.
Понятие о магнитном поле Земли
Земной шар является естественным постоянным магнитом, вокруг которого существует магнитное поле. Средняя величина магнитной индукции вблизи земной поверхности равна .
Рис. 3.3.5. Геомагнитное поле Земли
Согласно современным представлениям, основная часть магнитного поля Земли (геомагнитного поля) имеет внутриземное происхождение. Это поле создается электрическими токами, протекающими в жидком металлическом ядре планеты. На расстояниях, не превышающих ( — радиус Земли), геомагнитное поле имеет структуру, изображенную на рис. 3.3.5. Она близка к структуре магнитного поля намагниченного шара (магнитного диполя). Радиус диполя порядка , его центр отстоит от центра Земли в сторону Тихого океана примерно на 450 км, ось диполя наклонена к оси вращения Земли на угол, равный 11,5°. Магнитные полюса Земли смещены относительно географических, причем в северном полушарии находится южный магнитный полюс с координатами 75°53′ северной широты, 100 °23′ западной долготы, а в южном полушарии — северный магнитный полюс N с координатами 66°06′ южной широты, 139°36′ восточной долготы. Незначительная часть (около 1 %) магнитного поля, окружающего Землю, создается электрическими токами, текущими в ионосфере — ионизованной части верхней атмосферы Земли.
На расстояниях, превышающих , структура магнитного поля Земли усложняется. Совместно с солнечным ветром (потоком заряженных частиц, испускаемым Солнцем), магнитное поле Земли формирует магнитосферу — многосвязную систему электрических и магнитных полей и потоков заряженных частиц. Магнитосфера несимметрична относительно дневной и ночной стороны Земли. С дневной стороны магнитосфера сжата солнечным ветром до расстояния , с ночной стороны она образует вытянутый «хвост», простирающийся на многие миллионы километров.
Рис. 3.3.6. Движение заряженных частиц в магнитном поле Земли
Магнитное поле Земли играет роль своеобразного «щита», защищающего все живое от потоков заряженных космических частиц (космических лучей). На больших расстояниях от Земли магнитное поле невелико, но захватывает громадные области пространства. Действуя на заряженные частицы длительное время, оно существенно изменяет их траектории, отклоняя потоки частиц от Земли. На расстояниях примерно от 500 до 60 000 км заряженные частицы движутся, навиваясь на линии индукции магнитного поля Земли (рис. 3.3.6). Они совершают колебания от одного магнитного полюса к другому с периодом от 0,1 до 1 с. Эта область космического пространства называется радиационным поясом Земли. Лишь в полярных областях небольшая часть таких частиц вторгается в верхние слои атмосферы из радиационного пояса Земли и вызывает полярные сияния.
Сила, действующая на проводник с током в магнитном поле. Закон Ампера
На проводник с током, находящийся в магнитное поле, действует сила Ампера:
(3.3.5) Рис. 3.3.7. Взаимодействие двух параллельных проводников с током
где — длина отрезка проводника с током , — угол между направлениями отрезка проводника и вектора магнитной индукции, — проекция вектора магнитной индукции на нормаль к проводнику. Направление силы Ампера определяется правилом буравчика: рукоятку буравчика вращают от вектора к вектору , тогда направление его поступательного движения определяет направление силы , или правилом левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по току, то отогнутый на 90° большой палец покажет направление действующей на участок проводника силы.
Между двумя параллельно расположенными бесконечно длинными проводниками, по которым протекают постоянные токи (рис. 3.3.7), возникает сила взаимодействия, направление и величина которой могут быть найдены из закона Ампера. Поскольку проводник с током находится в поле с индукцией , созданным проводником с током , сила Ампера направлена, как показано на рисунке. Проводники с одинаково направленными токами притягиваются, с противоположно направленными — отталкиваются. Модуль силы взаимодействия между участками единичной длины двух бесконечных параллельных проводников, расположенных на расстоянии друг от друга, равен
(3.3.6)
Действие магнитного поля на движущийся заряд. Сила Лоренца
На заряд , движущийся в магнитном поле со скоростью , действует сила Лоренца:
(3.3.7)
где — проекция вектора магнитной индукции на нормаль к скорости частицы. Направление силы Лоренца также определяется правилом левой руки или правилом буравчика. В однородном магнитном поле, вектор индукции которого перпендикулярен скорости заряженной частицы, она движется по окружности постоянного радиуса .
(3.3.8)
где — масса частицы, — абсолютное значение ее заряда, — скорость частицы, — индукция магнитного поля. Движение частицы происходит в плоскости, перпендикулярной вектору . Сила Лоренца в этом случае играет роль центростремительной силы. Ее работа всегда равна нулю, поскольку сила Лоренца в каждый момент времени перпендикулярна вектору мгновенной скорости частицы.
Магнитные свойства вещества. Гипотеза Ампера
Магнитные взаимодействия зависят от свойств среды, в которой они происходят. Физическая величина, показывающая, во сколько раз индукция магнитного поля в однородном веществе отличается от индукции магнитного поля в вакууме, называется магнитной проницаемостью вещества:
(3.3.9)
Согласно гипотезе Ампера магнитные свойства вещества определяются замкнутыми электрическими токами внутри него. В соответствии с современными представлениями, эти токи связаны с движением электронов в атомах вещества. Каждый электрон, движущийся в атоме вокруг ядра по замкнутой орбите, представляет собой элементарный электронный ток, магнитный момент которого, называемый орбитальным магнитным моментом, перпендикулярен плоскости орбиты.
Орбитальный магнитный момент атома равен векторной сумме орбитальных магнитных моментов его электронов. Если вещество состоит из молекул, то магнитный момент молекулы является векторной суммой орбитальных магнитных моментов ее атомов. Таким образом, атомы и молекулы в общем случае имеют магнитные моменты и могут создавать магнитное поле.
Магнетиками называются вещества, способные намагничиваться во внешнем магнитном поле, т.е. создавать собственное (внутреннее) магнитное поле самого вещества. По своим свойствам магнетики подразделяются на слабомагнитные и сильномагнитные вещества. К слабомагнитным веществам относятся диамагнетики и парамагнетики. Основную группу сильномагнитных веществ составляют ферромагнетики.
Диамагнетиками называются вещества, у которых атомы или молекулы в отсутствие внешнего магнитного поля не имеют магнитных моментов. Диамагнетиками являются инертные газы, ряд металлов (золото, серебро, ртуть, цинк, медь), вода, стекло, многие органические соединения. При внесении диамагнитного вещества в магнитное поле в каждом его атоме (или молекуле) индуцируется дополнительный атомный (или молекулярный) ток с некоторым магнитным моментом. Этот ток имеет такое направление, что создаваемое им магнитное поле противоположно внешнему полю. Вектор магнитной индукции внутреннего поля направлен против внешнего поля и ослабляет его. В этом и состоит намагничивание диамагнетиков, для которых . Диамагнетизм является очень слабым эффектом. Магнитная проницаемость даже самых сильных диамагнетиков отличается от единицы не более, чем десятитысячные доли.
Атомы (или молекулы), обладающие в отсутствие внешнего поля небольшим магнитным моментом, называются парамагнитными, а состоящие из них вещества — парамагнетиками. К парамагнетикам относятся кислород, окись азота, алюминий, платина, щелочные и щелочноземельные металлы и др. В отсутствие внешнего магнитного поля тепловое движение атомов (молекул) парамагнетика препятствует возникновению упорядоченного расположения магнитных моментов отдельных атомов (молекул), и собственного магнитного поля в веществе не возникает. При внесении парамагнетика во внешнее магнитное поле атомные (молекулярные) токи стремятся расположиться так, чтобы их магнитные моменты были параллельны вектору индукции внешнего поля. Совместное действие магнитного поля и теплового движения приводит к тому, что возникает преимущественная ориентация магнитных моментов атомов (молекул) по направлению внешнего поля. В парамагнитном веществе создается собственное (внутреннее) магнитное поле, вектор индукции которого направлен одинаково с вектором индукции внешнего поля. Для парамагнетиков , но эффект парамагнетизма очень слаб; магнитная проницаемость даже для наиболее сильных парамагнетиков отличается от единицы не более, чем на тысячные доли.
Ферромагнетики
Ферромагнетиками называется группа веществ в твердом кристаллическом состоянии, обладающих магнитными свойствами, обусловленными особым взаимодействием атомных носителей магнетизма. К ферромагнетикам относятся железо, никель, кобальт, а также ряд сплавов. Ферромагнетизм объясняется квантовыми магнитными свойствами электронов. Дело в том, что электрон, независимо от его пребывания в какой-либо системе частиц (атом, молекула, кристалл), обладает собственным моментом импульса (спином) и связанным с ним собственным (спиновым) магнитным моментом. Важная особенность спина электрона состоит в том, что в магнитном поле (как внешнем, так и созданном атомными и молекулярными токами) спин может быть ориентирован так, чтобы его проекция на направление вектора магнитной индукции принимала только два значения, равные по модулю и противоположные по знаку.
В результате этого, в некоторых кристаллах, например в кристаллах железа, возникают условия для параллельной ориентации собственных магнитных моментов электронов группы атомов.
Внутри кристалла ферромагнетика образуются намагниченные области размером порядка см, в которых спины электронов параллельны. Эти самопроизвольно намагниченные области называются доменами. В отдельных доменах магнитные поля имеют различные направления и в большом кристалле взаимно компенсируют друг друга. При внесении ферромагнитного образца во внешнее магнитное поле происходит частичное упорядочение ориентации магнитных моментов отдельных доменов и результирующая магнитная индукция в веществе растет. С увеличением магнитной индукции внешнего поля степень упорядоченности доменов повышается. При некотором значении индукции внешнего поля наступает полное упорядочение ориентации доменов и возрастание магнитной индукции в веществе прекращается. Это явление называется магнитным насыщением. В состоянии насыщения магнитная проницаемость ферромагнетиков имеет очень большие значения; например, для железа , для пермаллоя (сплав никеля с железом) .
При отключении внешнего магнитного поля значительная часть доменов в ферромагнитном образце сохраняет упорядоченную ориентацию — образец становится постоянным магнитом. Упорядоченность ориентации доменов в ферромагнетике нарушается тепловыми колебаниями атомов в кристалле. Чем выше температура, тем интенсивнее разрушается порядок в ориентации доменов, в результате чего образец размагничивается. Температура, выше которой вещество теряет свойства ферромагнетика, называется температурой Кюри. Температура Кюри у железа 770 °C, у никеля 356 °C, у кобальта 1130 °C.
Указания по решению задач
Большинство задач данного раздела связано либо с равновесием, либо с движением тел под действием различных сил, включая силу Ампера и силу Лоренца. Поэтому, наряду с законами магнетизма и электромагнитной индукции, при решении задач необходимо использовать законы механики.
Примеры решения задач
Задача №3.3.1.
Частица массой г, несущая заряд Кл, движется в плоскости, перпендикулярной однородному магнитному полю с индукцией Тл. Найти период обращения частицы Т. Силу тяжести не учитывать.
Решение:
Со стороны магнитного поля на частицу действует сила Лоренца, перпендикулярная скорости частицы и индукции .
Под действием этой силы частица совершает движение по окружности радиусом , описываемое уравнением где — масса частицы. Учитывая, что период обращения частицы связан с ее скоростью и радиусом окружности соотношением получаем ответ:
Задача №3.3.2.
Заряженная частица массой кг влетает со скоростью в область с постоянным и однородным магнитным полем, вектор индукции которого перпендикулярен . На какой угол отклонится частица, если область, занимаемая магнитным полем, в котором движется частица, ограничена плоскостями, перпендикулярными , расстояние между которыми ? Заряд частицы , индукция магнитного поля В = 0,01 Тл. Силу тяжести не учитывать.
Решение:
Как только частица окажется в области, занимаемой магнитным полем, на нее начнет действовать сила Лоренца, направленная перпендикулярно скорости частицы. Под действием этой силы частица будет двигаться по дуге окружности радиусом R, который легко найти из уравнения движения (см. решение задачи 3.3.1): .Из рисунка видно, что угол а, на который отклонится частица, определяется
соотношением между радиусом дуги R и длиной L области, занимаемой магнитным полем. В частности, при R > L Если , то частица опишет в области, занимаемой полем, полуокружность, и . Таким образом, ответ к задаче может быть сформулирован следующим образом: При числовых данных из условия задачи .
Задача №3.3.3.
Квадратная проволочная рамка может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из ее сторон. Рамка помещена в однородное магнитное поле с индукцией , направленной вертикально. Когда по рамке течет ток , она отклоняется от вертикальной плоскости на угол . Определить индукцию магнитного поля В, если площадь сечения проволоки, из которой изготовлена рамка, , а плотность материала проволоки . Ускорение свободного падения принять .
Решение:
Силы, действующие на отдельные отрезки рамки со стороны магнитного поля (силы Ампера ), изображены на рисунке а. Видно, что отклонение рамки от вертикали вызывает сила , приложенная к нижнему горизонтальному отрезку. Сила приложена к оси, на которой вращается рамка, а силы и действуют в плоскости рамки и могут вызвать только ее деформацию. Таким образом, рамка находится в равновесии под действием сил, изображенных на рисунке б, где — сила Ампера, — масса рамки, — длина одной из ее сторон, — сила реакции оси. Уравнение моментов относительно оси вращения рамки имеет вид: Объединяя записанные выражения, после несложных преобразований получаем ответ: