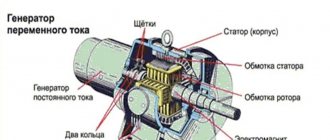
- How is strength measured?
Force:
When studying natural phenomena, different physical quantities are used. In order to describe qualitatively and quantitatively the interaction of bodies, a physical quantity is introduced, which is called force.
Definition of strength
Force is a physical quantity that serves as a measure of the interaction of bodies and causes changes in the speeds of bodies or their parts.
Observation. If we consider, for example, the interaction of a hand with a volleyball, then we say: “The ball exerts a force on the hand or the hand exerts a force on the ball.”
Experience. Let's hang an apple on a spring (Fig. 66).
The spring will lengthen. If you hang two apples on it, it will lengthen more. So, two apples exert a greater force on the spring than one.
The result of the action of one body on another depends on the value of the applied force.
The tighter the door is closed, the more force we have to push or pull it to open it.
To make it easier to open the door, its handle is attached as far as possible from the hinges. Try opening the door by pushing it at a point located near the hinges. You will find that this is much more difficult to do than with a pen. The result of the action of one body on another depends on the point of application of the force.
To achieve a certain result of an action, for example, stretching or compressing a spring, closing or opening a door, you need to apply forces in different directions.
The action of one body on another depends on the direction of the force.
Graphically, force is depicted as a straight line segment with an arrow at the end (Fig. 67).
The beginning of the segment is combined with the point of application of force. The length of a segment on a certain scale is equal to the value of the force. The arrow shows the direction of the force. Quantities that, in addition to their numerical value, are also characterized by a direction in space are called vectors, or vectors (from the Latin word vector - leading, carrying).
Why do bodies change their state in space?
Any changes in nature occur as a result of interaction between bodies. To change the position of the car on the rails, railway workers send a locomotive towards it, which displaces the car from its place and puts it in motion (Fig. 32).
A sailboat can stand near the shore for a long time until a fair wind blows and affects its sails (Fig. 33). The wheels of a toy car can rotate at any speed, but the toy will not change its position unless a board or ruler is placed under the toy (Fig. 34). The shape or size of a spring can be changed only by hanging a weight from it or by pulling one of its ends with your hand.
All bodies in nature are connected in one way or another and act on each other either directly or through physical fields. This action is always reciprocal. If a diesel locomotive acts on a car and changes its speed, then the speed of the diesel locomotive also changes due to the reverse action of the car. The Sun acts on all bodies on Earth and on the Earth itself, keeping it in orbit. But the Earth also attracts the Sun and, in turn, changes its trajectory. Thus, in all cases we can only talk about the mutual action of bodies - interaction.
During interaction, the speeds of bodies or their parts can change.
However, interacting with different bodies, a given body will change its speed in different ways. Thus, a sailboat can acquire speed due to the action of wind on it. But the same result can be obtained by turning on the engine located on the sailboat. A sailboat can also move a boat by acting on it through a cable. In order not to name all the interacting bodies each time, all these actions are united by one concept of force.
International System of Units and Newton
This name refers to the system of measures and quantities, which is briefly designated SI (from the French Système International). It is based on 7 basic physical quantities (ampere, kelvin, second, candela, kilogram, meter and mole). The SI was adopted in 1960, and in 1971 a final fundamental quantity, the mole, was added.
The SI unit of force is the newton. It is understood as a category that, acting on a body with a mass of 1 kg, accelerates its movement by 1 m/s for every second of time. In Russian, Newton's notation [N] is accepted; in Latin it is written as [N].
The use of prefixes approved in the SI to the basic units of measurement makes it possible to obtain their fractional or large values. For force, this could be, for example, µN (micronewton, 1 µN = 10-6 N), mN (millinewton, 1 mN = 10-3 N) or kN (kilonewton, in newtons this is 1000 N).
It is interesting to note that the newton is not one of the 7 fundamental units of force in the SI system, so it is a derived unit. In particular, 1 [N] = 1 [kg*m/s2], that is, it is expressed in terms of kilogram (mass), meter (distance) and second (time).
Let's force the topic
In the world around us, we cannot avoid encountering forces: forces are used to open a door, press keys on a keyboard, drive a car, climb the stairs to the Statue of Liberty, pull a wallet out of a pocket, talk, and even breathe. The force is invisibly present everywhere: while walking, skating, chewing a hot dog, opening a bottle or blinking your beloved companion's eyelashes. Force is inextricably linked to the movement of objects, and physics helps us understand how this relationship works.
Power is actually quite a funny topic. Like other physics topics, it seems difficult only until you actually get to know it. Like our old friends, displacement, velocity and acceleration (see Chapters 3 and 4), force is a vector, i.e. has magnitude and direction.
Sir Isaac Newton was the first to include force, mass and acceleration in one equation in the 17th century. (Remember the historical anecdote about an apple falling on his head, as a result of which he supposedly figured out how to mathematically describe the force of gravity. More on this in Chapter 6, where Newton is also one of the main characters.)
Newton's laws and the speed of light
Newton's laws were revised by Albert Einstein in his theory of relativity. It showed that Newton's laws do not hold true for motion at speeds close to the speed of light. The basic idea of relativity is that the speed of light is the fastest possible speed. This means that any interaction can only occur at this speed or less. Therefore, when approaching this speed, the changing nature of the interaction must be taken into account; For example, measuring the length of a rocket moving at the speed of light will be different from measuring the length of a stationary rocket. As will be shown in Chapter 21, Einstein's theory of relativity greatly changed Newton's view of the world and its laws.
As often happens with many physical discoveries, Newton first carefully observed the behavior of objects, mentally modeled it, and then expressed it in mathematical form. If you know the basics of vectors (covered in Chapter 4), this math will be fairly straightforward.
Newton described his model using three statements that are now called Newton's laws. However, we must remember that in fact these are not the final “laws of nature”, because physicists can only create models of nature, which are often subsequently revised and refined.
Heavier - Lighter
The weight of a body ${\large P}$ is expressed by the product of its mass ${\large m}$ and the gravitational acceleration ${\large g}$.
${\large P = m \cdot g}$
When on earth a body becomes lighter (presses less on the scales), this is due to a decrease in mass. On the moon, everything is different; the decrease in weight is caused by a change in another factor - ${\large g}$, since the acceleration of gravity on the surface of the moon is six times less than on the earth.
mass of the earth = ${\large 5.9736 \cdot {10^{24}}\ kg }$
moon mass = ${\large 7.3477 \cdot {10^{22}}\ kg }$
acceleration of gravity on Earth = ${\large 9.81\ m / c^2 }$
gravitational acceleration on the Moon = ${\large 1.62 \ m / c^2 }$
As a result, the product ${\large m \cdot g }$, and therefore the weight, decreases by 6 times.
But it is impossible to describe both of these phenomena with the same expression “make it easier.” On the moon, bodies do not become lighter, but only fall less rapidly; they are “less epileptic”))).
Particle trajectories
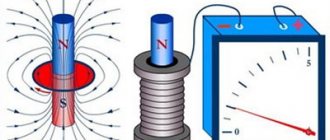
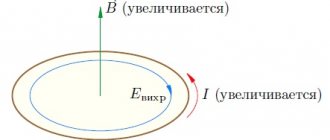
The interaction of a magnetic field with a charge is widely used in mass spectrographs in the study of elementary particles.
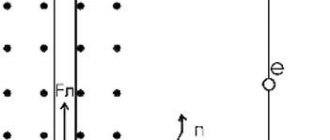
The action of the field in this case causes the appearance of a force called the Lorentz force. When a charged particle moving at a certain speed enters a magnetic field, the formula of which is F = vBqsinα, causes the particle to move in a circle.
In this mathematical model, v is the modulus of the velocity of a particle whose electric charge is q, B is the magnetic induction of the field, α is the angle between the directions of velocity and magnetic induction.
The particle moves in a circle (or arc of a circle), since the force and speed are directed at an angle of 90 ° to each other. Changing the direction of linear velocity causes acceleration to appear.
The rule of the left hand, discussed above, also occurs when studying the Lorentz force: if the left hand is positioned in such a way that the magnetic induction vector enters the palm, four fingers extended in a line are directed along the speed of a positively charged particle, then bent by 90 ° the thumb will indicate the direction of the force.
Center of mass
The point of the center of mass is remarkable in that if a great many forces act on the particles forming a body (no matter whether it is solid or liquid, a cluster of stars or something else) (meaning only external forces, since all internal forces compensate each other), then the resulting the force leads to such an acceleration of this point as if the entire mass of the body ${\large m}$ were in it.
The position of the center of mass is determined by the equation:
${\large R_{cm} = \frac{\sum m_i\, r_i}{\sum m_i}}$
This is a vector equation, i.e. in fact, three equations - one for each of the three directions. But consider only the ${\large x}$ direction. What does the following equality mean?
${\large X_{cm} = \frac{\sum m_i\, x_i}{\sum m_i}}$
Suppose the body is divided into small pieces with the same mass ${\large m}$, and the total mass of the body will be equal to the number of such pieces ${\large N}$ multiplied by the mass of one piece, for example 1 gram. Then this equation means that you need to take the ${\large x}$ coordinates of all the pieces, add them up and divide the result by the number of pieces. In other words, if the masses of the pieces are equal, then ${\large X_{cm}}$ will be simply the arithmetic mean of the ${\large x}$ coordinates of all the pieces.
| center of mass of a complex body lies on the line connecting the centers of mass its two constituent parts |
Plasma problems
The interaction of a magnetic field and matter is used in cyclotrons. Problems associated with the laboratory study of plasma do not allow it to be kept in closed vessels. High can only exist at high temperatures. Plasma can be kept in one place in space using magnetic fields, twisting the gas in the form of a ring. Controlled ones can also be studied by twisting high-temperature plasma into a cord using magnetic fields.
An example of the effect of a magnetic field under natural conditions on ionized gas is the Aurora Borealis. This majestic spectacle is observed above the Arctic Circle at an altitude of 100 km above the earth's surface. The mysterious colorful glow of the gas could only be explained in the 20th century. The earth's magnetic field near the poles cannot prevent the solar wind from entering the atmosphere. The most active radiation, directed along magnetic induction lines, causes ionization of the atmosphere.
Law of gravitation
Every object in the Universe is attracted to every other object with a force proportional to their masses and inversely proportional to the square of the distance between them.
${\large F = G \cdot \dfrac {m \cdot M}{R^2}}$
We can add that any body reacts to a force applied to it with acceleration in the direction of this force, in magnitude inversely proportional to the mass of the body.
${\large G}$ — gravitational constant
${\large M}$ — mass of the earth
${\large R}$ — radius of the earth
${\large G = 6.67 \cdot {10^{-11}} \left ( \dfrac {m^3}{kg \cdot {sec}^2} \right ) }$
${\large M = 5.97 \cdot {10^{24}} \left ( kg \right ) }$
${\large R = 6.37 \cdot {10^{6}} \left ( m \right ) }$
Within the framework of classical mechanics, gravitational interaction is described by Newton's law of universal gravitation, according to which the force of gravitational attraction between two bodies of mass ${\large m_1}$ and ${\large m_2}$ separated by a distance ${\large R}$ is
${\large F = -G \cdot \dfrac {m_1 \cdot m_2}{R^2}}$ Here ${\large G}$ is the gravitational constant equal to ${\large 6.673 \cdot {10^{- 11}} m^3 / \left ( kg \cdot {sec}^2 \right ) }$. The minus sign means that the force acting on the test body is always directed along the radius vector from the test body to the source of the gravitational field, i.e. gravitational interaction always leads to the attraction of bodies. The gravity field is potential. This means that you can introduce the potential energy of gravitational attraction of a pair of bodies, and this energy will not change after moving the bodies along a closed loop. The potentiality of the gravitational field entails the law of conservation of the sum of kinetic and potential energy, which, when studying the motion of bodies in a gravitational field, often significantly simplifies the solution. Within the framework of Newtonian mechanics, gravitational interaction is long-range. This means that no matter how a massive body moves, at any point in space the gravitational potential and force depend only on the position of the body at a given moment in time.
Superposition principle
Experience shows that if several other bodies act on a given body, then the corresponding forces add up as vectors. More precisely, the principle of superposition is valid. The principle of superposition of forces. Let the forces ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ act on the body. If we replace them with one force ${\large \overrightarrow{F} = \overrightarrow{F_1 } + \overrightarrow{F_2} \ldots + \overrightarrow{F_n}}$, then the result of the impact will not change. The force ${\large \overrightarrow{F}}$ is called the resultant of the forces ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ or the resultant force.
Examples of using
With average gravity on Earth (relatively, g = 9.806 65 m/s2), the mass of 1 kilogram exerts a force of about 9.8 newtons. An average sized apple involves about one newton of force, which we measure as the weight of the apple.
1 N = 0.10197 kg × 9.80665 m/s2 (0.101 97 kg = 101.97 g)
The average adult's weight exerts a force of about 608 N.
608 N = 62 kg × 9.80665 m/s2 (where 62 kg is the average mass of an adult in the world)
Body weight
Yes, don’t be surprised, body weight is also the force with which the body presses on a support or some kind of suspension (if the body is hanging).
You already know that all bodies are attracted to the Earth, and this force is called gravity. Look carefully at the picture. In this case, the bench prevents the boy and the cat from falling, and it is the bench that experiences the force arising from the gravity of the Earth.
Body weight is the force with which any body acts on a support or suspension due to gravity