Появление электрического тока наступает при замыкании цепи, когда на зажимах возникает разность потенциалов. Перемещение свободных электронов в проводнике осуществляется под действием электрического поля. В процессе движения, электроны сталкиваются с атомами и частично передают им свою накопившуюся энергию. Это приводит к уменьшению скорости их движения. В дальнейшем, под влиянием электрического поля, скорость движения электронов снова увеличивается. Результатом сопротивления становится нагревание проводника, по которому течет ток. Существуют разные способы расчетов этой величины, в том числе и формула удельного сопротивления, применяющаяся для материалов с индивидуальными физическими свойствами.
Опыты по установлению величин, от которых зависит сопротивление
Причина электрического сопротивления кроется во взаимодействии электронов с ионами кристаллической решетки металла. Логично предположить, что сопротивление будет зависеть от рода вещества, из которого он состоит. Также мы предположим, что есть некоторая зависимость от длины проводника и площади его поперечного сечения.
Теперь давайте проведем опыты, которые подтвердят или опровергнут наши предположения.
Соберем электрическую цепь из источника тока, ключа, амперметра и реостата. Реостат — это прибор, который позволит нам изменять силу тока в цепи. Подробнее о нем вы узнаете в отдельном уроке.
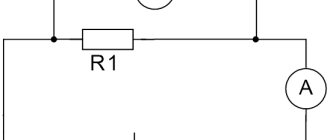
В эту цепь мы будем поочередно подключать различные проводники. К ним же параллельно подсоединим вольтметр (рисунок 1).
Рисунок 1. Определение зависимости сопротивления проводника от его размеров и рода вещества
Какие проводники мы будем подключать в цепь?
Вариантов может быть огромное множество. Мы рассмотрим следующие:
- Никелиновые проволоки одинаковой толщины (с одинаковой площадью поперечных сечений), но разной длины
- Такие же никелиновые проволоки, но теперь одинаковой длины и разной толщины (с различной площадью поперечных сечений)
- Никелиновую и нихромовую проволоки одинаковой длины и толщины
Каждый раз мы будем фиксировать значения силы тока в цепи, показанные амперметром. Вольтметр даст нам значения напряжения на концах каждого проводника.
Далее, используя закон Ома для участка цепи, мы сможем рассчитать сопротивление каждого проводника по формуле $I = \frac{U}{R}$.
Что такое электрическое сопротивление
Позиционируется как сопротивление некоторого элемента, служащего проводником. Он имеет единичную длину, показатель площади сечения. В этом заключается физический смысл. Электрическое сопротивление – это параметр проводника, опирающийся на зависимость от:
- структуры материала;
- параметра формы;
- габаритов изделия.
Результаты опытов
Какие выводы мы сможем сделать после всех расчетов?
- Из двух никелиновых проволок с одинаковой толщиной большее сопротивление имеет более длинная проволока
- Большее сопротивление имеет та никелиновая проволока, у которой поперечное сечение меньше. При этом длина проволок была одинаковой
- Никелиновая и нихромовая проволоки имеют разное сопротивление при одинаковых размерах
Сопротивление проводника
По своему сопротивлению тела делятся на три класса: проводники, непроводники (изоляторы) и полупроводники. Это деление условно, так как в природе не существует абсолютных проводников и абсолютных изоляторов.
Далее под проводником следует понимать металлическое тело.
Сопротивление проводника зависит от следующих факторов: рода материала, размеров, примесей, деформаций, температуры.
Сопротивление однородного проводника длиной l и сечения S составляет (при заданной температуре):
R = ρ l S , R=\rho \frac{l}{S}, R=ρSl,
где ρ ρ ρ (Ом·м/м2 или Ом·м) – коэффициент пропорциональности, его еще называют удельным сопротивлением материала, поскольку при l = 1 l = 1 l=1 и S = 1 S= 1 S=1 имеем ρ = R ρ=R ρ=R. В технике ρ ρ ρ выражают в единицах Ом·мм/м2
Величину, обратную к удельному сопротивлению, то есть γ = 1 / ρ γ = 1/ ρ γ=1/ρ, называют удельной проводимостью материала. Наименьшее ρ ρ ρ имеют серебро, медь, алюминий. В электротехнике проводники изготавливаются из меди или алюминия. При одинаковом сопротивлении алюминиевый проводник толще медного, но имеет меньшую плотность; кроме того, он дешевле и поэтому его целесообразнее использовать.
Удельное сопротивление
Если с длиной и толщиной проводника все просто и понятно, то что с веществом, из которого он состоит? Как учесть эту зависимость значения сопротивления? Для этого нужно вычислить удельное сопротивление вещества (проводника).
Что называется удельным сопротивлением проводника?
Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной $1 \space м$ и площадью поперечного сечения $1 \space м^2$.
Обозначается удельное сопротивление буквой $\rho$.
Не путать с плотностью вещества! Обращайте внимание на единицы измерения, чтобы не запутаться. Плотность в СИ измеряется в $\frac{кг}{м^3}$, а про единицу измерения удельного сопротивления мы поговорим чуть ниже.
Формула как найти
Согласно положению из любого учебного пособия по электродинамики, удельное сопротивление материала проводника формула равна пропорции общего сопротивления проводника на площадь поперечного сечения, поделенного на проводниковую длину. Важно понимать, что на конечный показатель будет влиять температура и степень материальной чистоты. К примеру, если в медь добавить немного марганца, то общий показатель будет увеличен в несколько раз.
Главная формула расчета
Интересно, что существует формула для неоднородного изотропного материала. Для этого нужно знать напряженность электрополя с плотностью электротока. Для нахождения нужно поделить первую величину на другую. В данном случае получится не константа, а скалярная величина.
Закон ома в дифференциальной форме
Есть другая, более сложная для понимания формула для неоднородного анизотропного материала. Зависит от тензорного координата.
Вам это будет интересно Назначение, устройство и принцип работы АВР
Важно отметить, что связь сопротивления с проводимостью также выражается формулами. Существуют правила для нахождения изотропных и анизотропных материалов через тензорные компоненты. Они показаны ниже в схеме.
Связь с проводимостью, выраженная в физических соотношениях
Единица удельного сопротивления
Чтобы определить единицу измерения удельного сопротивления обратимся к формуле $\rho = \frac{RS}{l}$.
Единица сопротивления — $1 \space Ом$, площади поперечного сечения — $1 \space м^2$, длины — $1 \space м$.
Подставим все это в формулу:
$[\rho] = \frac{1 \space Ом \cdot 1 \space м^2}{1 \space м} = 1 \space Ом \cdot м$.
Площадь поперечного сечения проводника обычно небольшая, поэтому ее удобно выражать в $мм^2$. Поэтому часто удельное сопротивление проводника измеряют в $\frac{1 \space Ом \cdot 1 \space мм^2}{1 \space м}$.
Где R имеет размерность Ом/квадрат.
Ширину резистивной линии принимают обычно не менее 0,2 мм, так как более узкая линия может приводить к обрывам из-за дефектов маски или подложки, а также из-за наличия случайных пылинок. Кроме того, чем уже линия, тем сильнее влияет зона подпыления или тень в щели маски на получение требуемого номинала сопротивления.
Практически установлено, что лучше всего изготавливать резисторы прямоугольной формы. При одной и той же толщине резистивной пленки можно получать различные сопротивления, отличающиеся по номиналу в десятки раз. Для этого достаточно изменять отношение длины пленки к ее ширине. Максимальная мощность, рассеиваемая на резисторе, ограничена ее допустимой температурой и зависит от теплопроводности подложки, ее материала, отношения площади, занятой резистором, к всей площади подложки, а также от выбранного способа охлаждения и температуры окружающей среды.
Материал, используемый для изготовления резистивных пленок, должен обеспечивать возможность получения широкого диапазона стабильных во времени сопротивлений, обладать низким температурным коэффициентом сопротивления и высокой коррозийной стойкостью. При напылении он должен образовывать тонкие, четкие линии с хорошей повторяемостью их от образца к образцу. Характеристики некоторых материалов, применяемых при изготовлении тонкопленочных резисторов, приведены в табл. 3.
Таблица 3. Характеристики материалов пленочных резисторов
| Материал резистора | Материал контактных площадок | Удельное поверхностное сопротивление рs, Ом/квадрат | Температурный коэффициент сопротивления ТКR*104, 1/оC | Удельная мощность рассеивания Ро, Вт/см2 | Относительное изменение сопротивления за 1000ч работы, % | Способ нанесения пленок |
| Хром | Золото | 10-50 | -2,5 | 1,5-3 | Термическое напыление | |
| Нихром | Медь | +1 -1 | 1,1-1,3 | То же | ||
| Сплав МЛТ-3М | Медь с подслоем нихрома (ванадия) | +2 -2 | +0,5 -0,5 | » | ||
| Рений | — | 300-7000 | 0-20 | — | — | » |
| Тантал | Алюминий с подслоем нихрома (ванадия) | 20-100 | -2 | Катодное напыление | ||
| Тантал | Тантал | -2 | То же | |||
| Нитрид тантала | » | 0,2 | » | |||
| Сплав РС3001 | Золото с подслоем хрома | 1000-2000 | -0,2 | +0,5 -0,5 | Термическое напыление | |
| Кермет | » » » | 3000-10000 | -5 -:- +3 | +1 -1 | То же | |
| Паста ПР | Пастп ПП | 5-100000 | -12 -:- +10 | +3 -3 | Сеткография |
Следует отметить, что указанные в таблице значения являются ориентировочными, так как они существенно зависят от метода нанесения пленки и режима ее обработки. Удельное сопротивление пленки определяется как ее составом, так и структурой, которая изменяется в процессе термообработки.
Рис. 4. Зависимость удельного сопротивления пленки от ее толщины: I-область туннельного эффекта; II-область нарушенной поверхности; III-область объемных свойств.
На рис. 4 показана типичная зависимость удельного сопротивления пленки от ее толщины. При малых толщинах свойства пленки существенно зависят от характера микронеровностей на поверхности подложки. В этой области могут наблюдаться нарушения непрерывности структуры пленки. Проводимость здесь обусловлена туннельным эффектом и термоэлектронной эмиссией между отдельными кристаллитами. Наиболее целесообразно использовать пленки такой толщины, при которой становятся заметными их объемные свойства. В этом случае легче регулировать толщину пленки, а нарушения поверхности не имеют большого значения.
Металлическая пленка толщиной порядка 1нм независимо от природы металла имеет большое удельное электрическое сопротивление, которое экспоненциально уменьшается с увеличение толщины. Пленки такой малой толщины весьма не стабильны и почти не применяются. Для того чтобы заведомо получить сплошную пленку при имеющихся в производстве отклонениях от выбранного технологического режима, считают, что толщина пленки, наносимая вакуумным испарением, должна быть порядка 100 нм. Следует отметить, что пленки тугоплавких металлов могут быть более тонкими, так как они обладают более стабильными характеристиками.
Тонкопленочные резисторы можно изготавливать из металлов, сплавов (в том числе многокомпонентных), полупроводников и керметов(смесей металлов с керамикой).
Широкое распространение находит хромированный сплав (20% хрома и 80% никеля). Поверхностное сопротивление пленки из этого сплава достигает 300 Ом/квадрат при малом температурном коэффициенте сопротивления. Температура испарения сплава значительная(1600оС), причем для получения высококачественного пленочного резистора подложка должна нагреваться до 300-350оС. Из сплава железа с хромом(79% железа, 21% хрома) и железоникелевого сплава (71,5% железа, 21% хрома, 7,5% никеля) изготавливают пленки, обладающие сопротивлением 150 Ом/квадрат, с температурным коэффициентом сопротивления не более 1*10-4 1/оС. Значительно большее поверхностное сопротивление (до 400 Ом/квадрат) имеет многокомпонентный сплав, состоящий из 74% никеля, 20% хрома, 3% железа и 3% алюминия.
Стабильность металлических пленок зависит до некоторой степени от температуры плавления металла, его плотности и возможности образования стабильности окисного поверхностного слоя. Как правило, чем выше температура плавления, тем лучше стабильность пленки. Вольфрам образует высокостабильные пленки в вакууме, однако они нестабильны в воздухе. Свойствами, обеспечивающими образование высокостабильных пленок, обладает рений – тугоплавкий металл, который находит все большее применение для получения пленочных резисторов.
В случае, когда необходимо получить высокостабильные пленки с большим поверхностным сопротивлением (несколько тысяч Ом на квадрат) и малым температурным коэффициентом сопротивления, применяют тантал. Это объясняется еще и тем, что поверхность тантала легко покрывается пленкой окиси и становится малоактивной, хотя сам металл относится к активным; тонкий прозрачный поверхностный слой окиси хорошо связан с танталом, обладает высоким сопротивлением износу и коррозии в различных атмосферных условиях и не поддается воздействию многих кислот; реакция окисления тантала легко управляется и может быть использована для регулирования толщины пленки и ее сопротивления; пятиокись тантала является хорошим диэлектриком, что позволяет использовать его для изготовления и пленочных конденсаторов.
Большим поверхностным сопротивлением (до 10000 Ом/квадрат) обладают пленки из сплава, содержащего 24% хрома и 76% кремния. Напыление пленок в данном случае производится по методу «вспышки», при котором порошок или небольшие кусочки сплава падают на разогретый до высокой температуры вольфрамовый испаритель. Образующееся при этом облако пара конденсируется на подложке, нагретой до 200-500оС. Полученные таким путем пленки отличаются малым температурным коэффициентом сопротивления (5*10-5 1/оС) и высокой стабильностью (после 2000ч работы изменение сопротивления не превышает 0,2%, а после 5000ч – 3%).
Еще большим поверхностным сопротивлением (до 50000 Ом/квадрат) обладают пленки из керметов. Типичными керметами являются пленки палладиево-серебряной глазури или танталово-хромового стекла. Резисторы на основе этих пленок используют в схемах, где допустим высокий температурный коэффициент сопротивления. Наиболее удачна пленка из смеси из моноокиси кремния и хрома. Она однородна, стабильна, имеет высокие адгезионные свойства, высокую теплостойкость и хорошие механические свойства. Сопротивление пленки изменяется в широких пределах в зависимости от состава смеси. Наилучшие характеристики имеют пленки, содержащие 70% хрома и 30% моноокиси кремния. Испарение смеси производится с вольфрамовой спирали при температуре 1300-1600оС на подложку, нагретую до 200-250оС. После напыления пленки ее нагревают в контролируемой среде при температуре 400-450оС для стабилизации параметров.
Для регулирования осаждения резистивных пленок в рабочий объем вакуумной установки вблизи напыляемых подложек помещают контрольную подложку с серебряными контактами (свидетель). Когда сопротивление между контактами контрольной подложки достигает определенной величины, испарение прекращается поворотом заслонки. Как показывает опыт, сопротивление обычно уменьшается после того, как подложка извлекается из вакуумной системы, или при ее дальнейшей термообработке. Это объясняется тем, что атомы газа или другие примесные атомы сорбируются пленкой в процессе ее напыления, а затем при нагреве химически реагируют с ней. Другой причиной является возникновение в материале пленки напряжений, которые могут изменяться в процессе отжига.
Значения удельных сопротивлений некоторых веществ
В таблице 1 приведены значения удельных сопротивлений некоторых веществ.
| Вещество | $\rho$, $\frac{Ом \cdot мм^2}{м}$ | Вещество | $\rho$, $\frac{Ом \cdot мм^2}{м}$ |
| Серебро | $0.016$ | Манганин (сплав) | $0.43$ |
| Медь | $0.017$ | Константан (сплав) | $0.50$ |
| Золото | $0.024$ | Ртуть | $0.96$ |
| Алюминий | $0.028$ | Нихром (сплав) | $1.1$ |
| Вольфрам | $0.055$ | Фехраль (сплав) | $1.3$ |
| Железо | $0.10$ | Графит | $13$ |
| Свинец | $0.21$ | Фарфор | $10^{19}$ |
| Никелин (сплав) | $0.40$ | Эбонит | $10^{20}$ |
Таблица 1. Удельное сопротивление некоторых веществ (при $t = 20 \space \degree C$)
Обратите внимание, что эти значения актуальны при температуре $20 \space \degree C$.
Удельное сопротивление вещества зависит от температуры.
Опыты показали, что при определенной температуре для каждого вещества диэлектрик может стать проводником (полупроводник). Также экспериментально доказано, что с повышением температуры удельное сопротивление металлов увеличивается.
От чего зависит?
Зависит показатель от температуры и отличается в разных материалах.
Зависимость от температуры
В каждом наименовании материала он отличается, в частности:
- В проводниковых элементах при увеличении показателя температуры, возрастает.
- В то же время в полупроводниковых, а также диэлектриках на таких же условиях уменьшается.
Величину, которая учитывает параметр изменения, принято называть температурным коэффициентом.
Удельное сопротивление разных материалов
Рассмотрим показатель монокристаллов, при параметре температуры, равном 20 градусов.
| Олово | 9,9–14,3 |
| Висмут | 109–138 |
| Кадмий | 6,8–8,3 |
| Цинк | 5,91–6,13 |
| Теллур | 2,90х109–5,9х109 |
Таблица для металлов
В таблице приводятся показатели для металлов, а также отдельных сплавов. Разница параметров связана непосредственно с химической чистотой, методами отливки, непостоянством самого сплава.
| Серебро | 0,015–0,0162 |
| Медь | 0,01707–0,018 |
| Золото | 0,023 |
| Алюминий | 0,0262–0,0295 |
| Иридий | 0,0474 |
| Натрий | 0,0485 |
| Молибден | 0,054 |
| Вольфрам | 0,053–0,055 |
| Цинк | 0,059 |
| Индий | 0,0837 |
| Никель | 0,087 |
| Железо | 0,099 |
| Платина | 0,107 |
| Олово | 0,12 |
| Свинец | 0,217–0,227 |
| Титан | 0,5562–0,7837 |
| Ртуть | 0,958 |
| Висмут | 1,2 |
Использование веществ для изготовления проводников и изолятов
У каких веществ самые большие значения удельного сопротивления? Конечно, у диэлектриков. Например, эбонит и фарфор практически не проводят электрический ток. Поэтому их и используют в качестве изоляторов.
Самое меньшее удельное сопротивление имеют чистые металлы. Серебро и медь — лучшие проводники электричества.
Из каких веществ изготавливают проводники, применяемые на практике? Чаще всего для проводки электрических цепей используют медные, алюминиевые и железные провода.
В таблице 1 вы также могли обратить внимание на значения удельных сопротивлений для сплавов нескольких веществ. Они имеют достаточно большие значения. Зачем? Обычно их используют для изготовления приборов, которым необходимо для нормального функционирования иметь большое сопротивление, но все-таки пропускать ток.
Понятие сопротивление доходчиво
Это величина, определяющая способность полупроводникового элемента пропускать сквозь себя электрический ток. Дать общее понятие можно опираясь на основы строения металлов. Состоит металл из кристаллической решётки, между элементами которой путешествуют электроны. Внешнее поле заставит их при перемещении создавать электрический ток. Решётка позволяет им двигаться по заданному объёму, а электроны будут тереться о её узлы и не смогут протиснуться. Данное явление и называется сопротивлением, а именно: сила, которая будет мешать перемещению.
Ещё проще можно представить на основе ситечка, на раковине. Вода будет проходить медленнее, чем если бы проходила без него.
@yaklass.ru
Как вычислить?
Значение коэффициента можно определить из последнего уравнения. Таким образом мы получаем формулу удельного сопротивления: $ρ=R*{S \over L}$.
Каждое вещество характеризуется с помощью своего, индивидуального, значения . Поэтому, например, два совершенно одинаковых по длине и толщине (сечению) провода, но из разных металлов, будут иметь значительно отличающиеся сопротивления. Это связано с тем, что атомы различных веществ отличаются друг от друга массой, которая зависит от количества, протонов, нейтронов и электронов.