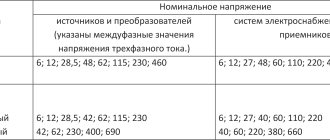
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
ho_t = ho_0 (1 + alpha t) ,) (
R_t = R_0 (1 + alpha t) ,)
где ρ
0,
ρ
t — удельные сопротивления вещества проводника соответственно при 0 °С и
t
°C;
R
0,
R
t — сопротивления проводника при 0 °С и
t
°С,
α
— температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент
сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ
.
Для всех металлических проводников α
> 0 и слабо изменяется с изменением температуры. У чистых металлов
α
= 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов)
n
= const и увеличение
ρ
происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α
-1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ
и
R
от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором
α
= const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости
. Металл переходит в сверхпроводящее состояние.
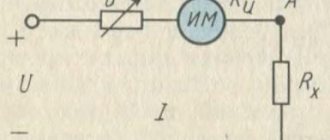
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
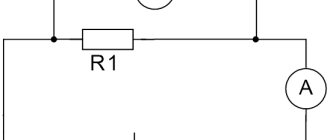
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.
последовательное соединение резисторов
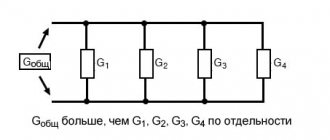
Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.
Получается, можно записать, что
формула при последовательном соединении резисторов
Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
Rобщее =R1 + R2 + R3 = 3+5+2=10 Ом.
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .
показать на реальном примере с помощью мультиметра Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.
Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .
сила тока через последовательное соединение проводников
Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами
Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.
Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.
Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?
Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Следовательно,
UR1 = IR1 =1×2=2 Вольта
UR2 = IR2 = 1×3=3 Вольта
UR3 = IR3 =1×5=5 Вольт
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Получается
U=UR1+UR2+UR3
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
ho_t = ho_0 (1 + alpha t) ,) (
R_t = R_0 (1 + alpha t) ,)
где ρ
0,
ρ
t — удельные сопротивления вещества проводника соответственно при 0 °С и
t
°C;
R
0,
R
t — сопротивления проводника при 0 °С и
t
°С,
α
— температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент
сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ
.
Для всех металлических проводников α
> 0 и слабо изменяется с изменением температуры. У чистых металлов
α
= 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов)
n
= const и увеличение
ρ
происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α
-1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ
и
R
от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором
α
= const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости
. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Низколегированные стали
Низколегированные стали способны чуть более сильно сопротивляться прохождению электричества, чем углеродистые. Их удельное электросопротивление составляет (20…43)·10 -8 Ом·м при комнатной температуре.
Следует отметить марки стали этого типа, которые наиболее плохо проводят электрический ток — это 18Х2Н4ВА и 50С2Г. Однако при высоких температурах, способность проводить электрический ток у сталей, приведенных в таблице, практически не различается.
Удельное электрическое сопротивление низколегированных сталей ρэ·10 8 , Ом·м
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
| 15ХФ | — | 28,1 | 42,1 | 60,6 | 83,3 | — | — | — |
| 30Х | 21 | 25,9 | 41,7 | 63,6 | 93,4 | 114,5 | 120,5 | 125,1 |
| 12ХН2 | 33 | 36 | 52 | 67 | — | 112 | — | — |
| 12ХН3 | 29,6 | — | — | 67 | — | 116 | — | — |
| 20ХН3 | 24 | 29 | 46 | 66 | — | 123 | — | — |
| 30ХН3 | 26,8 | 31,7 | 46,9 | 68,1 | 98,1 | 114,8 | 120,1 | 124,6 |
| 20ХН4Ф | 36 | 41 | 56 | 72 | 102 | 118 | — | — |
| 18Х2Н4ВА | 41 | 44 | 58 | 73 | 97 | 115 | — | — |
| 30Г2 | 20,8 | 25,9 | 42,1 | 64,5 | 94,6 | 114,3 | 120,2 | 125 |
| 12МХ | 24,6 | 27,4 | 40,6 | 59,8 | — | — | — | — |
| 40Х3М | — | 33,1 | 48,2 | 69,5 | 96,2 | — | — | — |
| 20Х3ФВМ | — | 39,8 | 54,4 | 74,3 | 98,2 | — | — | — |
| 50С2Г | 42,9 | 47 | 60,1 | 78,8 | 105,7 | 119,7 | 124,9 | 128,9 |
| 30Н3 | 27,1 | 32 | 47 | 67,9 | 99,2 | 114,9 | 120,4 | 124,8 |
Высоколегированные стали
Высоколегированные стали имеют удельное электрическое сопротивление в несколько раз выше чем углеродистые и низколегированные. По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10 -8 Ом·м.
При температуре 1300°С сопротивление высоко- и низко- легированных сталей становится почти одинаковым и не превышает 131·10 -8 Ом·м.
Удельное электрическое сопротивление высоколегированных сталей ρэ·10 8 , Ом·м
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
| Г13 | 68,3 | 75,6 | 93,1 | 95,2 | 114,7 | 123,8 | 127 | 130,8 |
| Г20Х12Ф | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — | — |
| Г21Х15Т | — | 82,4 | 95,6 | 104,5 | 112 | 119,2 | — | — |
| Х13Н13К10 | — | 90 | 100,8 | 109,6 | 115,4 | 119,6 | — | — |
| Х19Н10К47 | — | 90,5 | 98,6 | 105,2 | 110,8 | — | — | — |
| Р18 | 41,9 | 47,2 | 62,7 | 81,5 | 103,7 | 117,3 | 123,6 | 128,1 |
| ЭХ12 | 31 | 36 | 53 | 75 | 97 | 119 | — | — |
| 40Х10С2М (ЭИ107) | 86 | 91 | 101 | 112 | 122 | — | — | — |
Хромоникелевые аустенитные стали
Хромоникелевые аустенитные стали также являются нержавеющими, но за счет добавки никеля имеют удельное сопротивление почти в полтора раза выше, чем у хромистых — оно достигает величины (70…90)·10 -8 Ом·м.
Удельное электрическое сопротивление хромоникелевых нержавеющих сталей ρэ·10 8 , Ом·м
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 |
| 12Х18Н9 | — | 74,3 | 89,1 | 100,1 | 109,4 | 114 | — |
| 12Х18Н9Т | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — |
| 17Х18Н9 | 72 | 73,5 | 92,5 | 103 | 111,5 | 118,5 | — |
| Х18Н11Б | — | 84,6 | 97,6 | 107,8 | 115 | — | — |
| Х18Н9В | 71 | 77,6 | 91,6 | 102,6 | 111,1 | 117,1 | 122 |
| 4Х14НВ2М (ЭИ69) | 81,5 | 87,5 | 100 | 110 | 117,5 | — | — |
| 1Х14Н14В2М (ЭИ257) | — | 82,4 | 95,6 | 104,5 | 112 | 119,2 | — |
| 1х14Н18М3Т | — | 89 | 100 | 107,5 | 115 | — | — |
| 36Х18Н25С2 (ЭЯ3С) | — | 98,5 | 105,5 | 110 | 117,5 | — | — |
| Х13Н25М2В2 | — | 103 | 112,1 | 118,1 | 121 | — | — |
| Х7Н25 (ЭИ25) | — | — | 109 | 115 | 121 | 127 | — |
| Х2Н35 (ЭИ36) | 87,5 | 92,5 | 103 | 110 | 116 | 120,5 | — |
| Н28 | 84,2 | 89,1 | 99,6 | 107,7 | 114,2 | 118,4 | 122,5 |