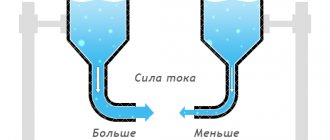
Зависимость показаний амперметра и вольтметра от используемого проводника в цепи
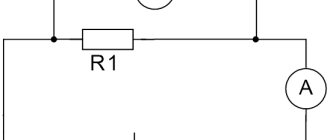
Для начала проведем интересный опыт. Соберем электрическую цепь из источника тока, ключа, амперметра и вольтметра. Также мы будем включать в эту цепь проводники из различных материалов. Они закреплены на специальной панели. К этим же проводникам мы будем параллельно подключать вольтметр (рисунок 1).
Проводники у нас обозначены следующим образом: AB — железная проволока, CD — никелиновая проволока, EF — медная проволока.
Эти проводники имеют одинаковую длину и сечение.
Рисунок 1. Зависимость силы тока от используемого в цепи проводника
Сначала подключим в цепь железную проволоку AB. Зафиксируем показания амперметра и вольтметра после замыкания ключа.
Теперь переключимся на никелиновую проволоку CD. Мы заметим, что сила тока в цепи уменьшилась.
Испробуем третий проводник: медную проволоку EF. Теперь сила тока значительно увеличилась.
Вы не забыли, что в нашем опыте был еще и вольтметр? Мы поочередно подключали его к каждому из проводников.
Каждый раз мы получали одинаковое значение напряжения. Оно не изменялось.
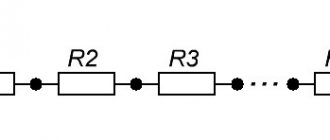
Мостовой метод
Устройства, применяемые для реализации такого измерения, именуют измерительными мостами. Четырехплечевой или одинарный мост содержит в себе две диагонали и четыре плеча:
Мост образуют три резистора, значения которых известны – R2, R3, R4 и соответственно сопротивление, значение которого необходимо измерить Rx. В одну из диагоналей моста необходимо подключить источник питания, для данного случая источник Е0 подключенный к зажимам a и b, а другую нулевой индикатор НИ (зажимы c и d), который выполняет роль указателя симметричности моста. Когда потенциалы в точках c и d будут равны, то отклонение в НИ протекает ток IНИ = 0 и его отклонение тоже равно нулю. Мост в состоянии равновесия. Будут выполнятся следующие соотношения: I1 = I2, I3 = I4, RxI1=R3I3, R2I2=R4I4. Учтя равенство токов и почленно разделив два последних уравнения получим:
Из данного выражения можем выделить искомое сопротивление:
Плечо R2 именуют плечом сравнения, а плечами отношений R3 и R4 соответственно.
Методом одинарного моста измеряют только средние сопротивления. Измерять им малые и большие сопротивления не рекомендуют. Нижний предел измерений моста (единицы Ом) ограничивается влиянием сопротивлений проводов и контактов, которые подключаются в плечо ас последовательно с объектом измерения Rх. Верхний предел (105 Ом) ограничен шунтирующим действием токов утечки.
Зависимость силы тока от свойств проводников
Вы уже знаете, что сила тока зависит от напряжения. Ведь напряжение является характеристикой электрического поля.
Но в нашем опыте напряжение оставалось постоянным. Значит, сила тока имеет еще одну зависимость.
Сила тока в цепи зависит от свойств проводников, включенных в электрическую цепь.
Метод непосредственной оценки
Чтоб реализовать такой метод необходимо применить омметр, схема которого ниже:
Данное устройство состоит из измерительного механизма ИМ (тип механизма магнитоэлектрический), шкала которого градуируется в омах. Также существует источник питания постоянным током U и резистор добавочный Rд. К выходным зажимам А и В производят подключения измеряемого сопротивления RX. Соответственно в цепи будет протекать ток:
Где RД, RИ, RХ – добавочный резистор и сопротивления измерительного механизма и соответственно объекта, который подлежит измерению. При этом угол отклонения стрелки прибора будет равен:
Где S1 – чувствительность токового измерителя.
Если зажимы А и В разомкнуть () , то угол отклонения стрелки прибора будет равен нулю α=0, а если их закоротить (R=0), то угол отклонения будет максимален. Поэтому у омметра шкала обратная – ноль у него справа.
Омметры довольно таки удобны в практическом применении, но они имеют довольно высокую погрешность (класс точности 2,5). Это связано с нестабильностью источника питания и неравномерностью шкалы. Дабы устранить причину неравномерности шкалы в омметрах стали использовать логометрические измерительные механизмы:
Такие приборы получили название мегомметров. Для получения источника питания в мегомметрах используют небольшие генераторы напряжением до 2500 Вольт и приводящиеся в движение вручную. В электронных же мегомметрах в качестве источника могут быть использованы батарейки или же внешний источник питания, подключаемый через специальный блок питания устройства. Мегомметры применяют для измерений больших сопротивлений, таких как сопротивление изоляции проводников. Для измерений свыше 109 Ома применяют специальные электронные устройства, которые носят название тераомметров.
Причины электрического сопротивления
В чем же причина сопротивления?
Вспомните урок «Электрический ток в металлах«. Электроны, двигаясь под действием электрического поля, обретают некоторое направление. Но при этом хаотичность их движения сохраняется. Мы еще сравнивали такое движение со стайкой мошкары, которую относит ветром.
Итак, электроны приведены в упорядоченное движение электрическим полем. При этом они взаимодействуют с ионами кристаллической решетки. Что при этом происходит? Упорядоченное движение замедляется. Теперь меньшее число электронов проходит через поперечное сечение проводника за $1 \space с$. Значит, уменьшается сила тока.
Сделаем вывод из наших рассуждений.
Причина сопротивления — это взаимосвязь движущихся электронов с ионами кристаллической решетки.
Логично, что разные проводники будут обладать разными значениями сопротивления. Все дело будет в различиях строения их кристаллической решетки. Кроме того, значение будут иметь длина проводника и площадь его поперечного сечения. Об этом мы поговорим в следующих уроках.
Постоянный ток
Господа, и снова всем здрастье! Мы с вами уже обсудили ток. Обсудили и напряжение. Осталась последняя сторона бермудского треугольника. Как многие уже догадались, речь сегодня пойдет про электрическое сопротивление. Что же это такое? От чего зависит? Как его рассчитать? Обо всем этом речь пойдет в сегодняшней статье!
А начиналось все это достаточно давно. В далекие и лихие 1800-е уважаемый господин Георг Ом игрался в своей лаборатории с напряжением и током, пропуская его через различные штуки, какие только могли его проводить. Будучи человеком наблюдательным, он установил одну интересную зависимость. А именно, что если взять один и тот же проводник, то сила тока в нем прямо пропорциональна приложенному напряжению. Ну, то есть если увеличить приложенное напряжение в два раза, то в два раза возрастет и сила тока. Соответственно, никто не мешает взять и ввести какой-нибудь коэффициент пропорциональности:
Где G – это и есть коэффициент, который называется проводимостью проводника. На практике же чаще люди оперируют с величиной, обратной проводимости. Она называется как раз-таки электрическое сопротивление и обозначается буковкой R:
Для случая электрического сопротивления, зависимость, полученная Георгом Омом выглядит так:
Господа, по большому секрету, мы только что написали закон Ома. Но не будем пока на этом концентрироваться. Для него у меня уже практически готова отдельная статья, в ней и поговорим об этом. Сейчас же более подробно остановимся именно на третьей составляющей этого выражения – на сопротивлении.
Во первых, это характеристика проводника. Сопротивление не зависит от тока с напряжением, кроме отдельных случаев типа нелинейных устройств. До них обязательно доберемся, но позже, господа. Сейчас мы рассматриваем обычные металлы и прочие милые и простые – линейные – штуки.
Измеряется сопротивление в Омах. Вполне логично – кто открыл, тот и назвал в честь себя. Отличный стимул для открытий, господа! Но помните, мы начали с проводимости? Которая у нас обозначается буковкой G? Так вот, она тоже имеет свою размерность – Сименсы. Но обычно на это всем пофиг, с ними почти никто не работает.
Пытливый ум непременно задастся вопросом – сопротивление, это конечно здорово, а от чего оно, собственно говоря, зависит? Ответы имеются. Давайте по пунктам. Опыт показывает, что сопротивление зависит по крайней мере от:
- геометрических размеров и формы проводника;
- материала;
- температуры проводника.
А теперь давайте подробнее по каждому из пунктов.
Господа, опыт показывает, что при постоянной температуре сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Ну, то есть чем проводник толще и короче, тем меньше его сопротивление. И наоборот, длинные и тонкие проводники имеют относительно высокое сопротивление. Это иллюстрирует рисунок 1. Данное утверждение понятно и по уже приводимой ранее аналогии электрического тока и водопровода: через толстую короткую трубу воде течь легче, чем через тонкую и длинную и возможна передача больших объемов жидкости за то же самое время.
Рисунок 1 – Толстый и тонкий проводники
Выразим это математическими формулами:
Здесь R – сопротивление, l – длина проводника, S – площадь его поперечного сечения.
Когда мы говорим, что кто-то кому-то пропорционален, всегда можно ввести коэффициент и заменить значок пропорциональности на значок равенства:
Как видим, здесь у нас появился новый коэффициент . Он называется удельным сопротивлением проводника.
Что же это такое? Господа, очевидно, что это то значение сопротивления, которое будет иметь проводник длиной 1 метр и площадью поперечного сечения 1 м2. А что там с его размерностью? Выразим из формулы:
Величина это табличная и она зависит от материала проводника.
Таким макаром мы плавно перешли ко второму пункту нашего перечня. Да, два проводника одинаковой формы и размеров, но из разного материала будут иметь разное сопротивление. И обусловлено это исключительно тем, что у них будет разное удельное сопротивление проводника. Приведем табличку со значением удельного сопротивления ρ для некоторых широко распространенных материалов.
Господа, видим, что меньше всех сопротивляется электрическому току у серебра, а у диэлектриков напротив, оно весьма большое. Это и понятно. Диэлектрики на то и диэлектрики, что бы ток не проводить.
Теперь, используя приведенную мною табличку (или гугл, если там нет нужного материала) вы легко сможете рассчитать себе провод с необходимым сопротивлением или же оценить, какое сопротивление будет у вашего провода с заданными площадью сечения и длиной.
Помнится, в моей инженерной практике был один подобный случай. Мы делали мощную установку для питания лампы накачки лазера. Мощности там были какие-то просто сумасшедшие. И для поглощения всей этой мощности на случай «если что-то пойдет не так », было принято решение изготовить резистор сопротивлением 1 Ом из какой-нибудь надежной проволоки. Почему именно 1 Ом и куда именно он устанавливался, мы сейчас не будем рассматривать. Это разговор для совсем другой статьи. Достаточно знать, что этот резистор должен был в случае чего принять в себя десятки мегаватт мощности и десятки килоджоулей энергии и желательно остаться при этом живым. Проштудировав списки доступных материалов, я выбрал два: нихром и фехраль. Они были жаростойкими, выдерживали высокие температуры, а кроме того обладали относительно высоким удельным электрическим сопротивлением, что позволяло с одной стороны брать не очень тонкие (они сразу перегорят) и не очень длинные (надо было влезть в разумные габариты) провода, а с другой – получить требуемые 1 Ом. В результате итеративных расчетов и анализа предложений рынка проволочной промышленности России (вот так термин), я-таки остановился на фехрали. Получилось, что проволока должна иметь диаметр несколько миллиметров и длиной в единицы метров. Точные цифры называть не буду, они мало кому из вас будут интересны, а мне лень искать эти выкладки в недрах архива. Был также рассчитан перегрев проволоки на случай (по формулам термодинамики), если действительно через нее пропустить десятки килоджоулей энергии. Он получился пара сотен градусов, что нас устраивало.
В заключении скажу, что данные самодельные резисторы были изготовлены и успешно прошли испытания, что подтверждает правильность приведенной формулы.
Однако мы слишком увлеклись лирическими отступлениями о случаях из жизни, совершенно забыв, что нам надо еще рассмотреть зависимость электрического сопротивления от температуры.
Давайте порассуждаем – а как теоретически может зависеть сопротивление проводника от температуры? Что нам известно про повышением температуры? Как минимум два факта.
Первое: с ростом температуры все атомы вещества начинают быстрее колебаться и с большей амплитудой. Это приводит к тому, что направленный поток заряженных частиц чаще и сильнее сталкивается с неподвижными частицами. Одно дело пробраться через толпу людей, где все стоят, и совсем другое – через такую, где все бегают, как сумасшедшие. Из-за этого средняя скорость направленного движения уменьшается, что эквивалентно уменьшению силы тока. Ну, то есть к росту сопротивления проводника току.
Второе: с ростом температуры увеличивается число свободных заряженных частиц в единице объема. Из-за большей амплитуды тепловых колебаний атомы легче ионизируются. Больше свободных частиц – больше сила тока. То есть сопротивление падает.
Итого в веществах с ростом температуры борются два процесса: первый и второй. Вопрос в том, кто победит. Практика показывает, что в металлах чаще победу одерживает первый процесс, а в электролитах – второй. Ну, то есть у металла сопротивление с ростом температуры растет. А если взять электролит (например, водичку с раствором медного купороса), то в нем сопротивление уменьшается при росте температуры.
Возможны случаи, когда первый и второй процессы полностью уравновешивают друг друга и сопротивление практически не зависит от температуры.
Итак, сопротивление имеет свойство меняться в зависимости от температуры. Пусть при температуре t1, было сопротивление R1. А при температуре t2 стало R2. Тогда что для первого случая, что для второго, можно записать следующее выражение:
Величина α, господа, называется температурным коэффициентом сопротивления. Этот коэффициент показывает относительное изменение сопротивления при изменении температуры на 1 градус. Например, если сопротивление какого-либо проводника при 10 градусах равно 1000 Ом, а при 11 градусах – 1001 Ом, то в этом случае
Величина это табличная. Ну то есть зависит от того, что именно за материал перед нами. Для железа, например, будет одно значение , а для меди – другое. Ясно, что для случая металлов (сопротивление с ростом температуры растет) α>0, а для случая электролитов (сопротивление с ростом температуры падает) α<0.
Господа, у нас за сегодняшний урок есть уже аж две величины, которые влияют на результирующее сопротивление проводника и при этом зависят от того, что же это за материал перед нами. Это ρ, которое удельное сопротивление проводника и α, которое температурный коэффициент сопротивления. Логично попытаться их свести между собой. Так и сделали! Что же в итоге получилось? А вот это:
Величина ρ0 не совсем однозначная. Это значение удельного сопротивления проводника при Δt=0. А поскольку не привязана ни к каким конкретным цифрам, а целиком и полностью определяется нами – пользователями – то и ρ получается тоже относительная величина. Оно равно значению удельного сопротивления проводника при некоторой температуре, которую мы примем за нулевую точку отсчета.
Господа, возникает вопрос – а где сие использовать? А, например, в термометрах. Например, есть такие платиновые термометры сопротивления. Принцип работы заключается в том, что мы измеряем сопротивление платиновой проволоки (оно, как мы сейчас выяснили, зависит от температуры). Эта проволока является датчиком температуры. И на основании измеренного сопротивления мы можем сделать вывод о том, какая температура окружающей среды. Эти термометры хороши тем, что позволяют работать в очень широком диапазоне температур. Скажем, при температурах в несколько сотен градусов. Мало какие термометры там еще смогут работать.
И просто как интересный факт – обычная лампа накаливания имеет в выключенном состоянии значение сопротивления гораздо меньшее, чем при работе. Скажем, у обычной 100-вт лампы сопротивление нити в холодном состоянии может быть примерно 50 – 100 Ом. Тогда как при штатной работе оно вырастает до величин порядка 500 Ом. Сопротивление вырастает почти в 10 раз! Но и нагрев тут в районе 2000 градусов! Кстати, вы можете на основании приведенных формул и измерения тока в сети попробовать более точно оценить температуру нити. Как? Подумайте сами . То есть при включении лампы через нее сначала течет ток, в несколько раз превышающий рабочий, особенно если момент включении попадет на пик синуса в розетке. Правда сопротивление мало весьма недолго, пока лампа не разогреется. Потом все выходит в режим и ток становится штатным. Однако такие броски тока являются одной из причин, почему лампы часто перегорают именно при включении.
На этом предлагаю закончить, господа. Статья получилась чуть больше, чем обычно. Надеюсь, вы не очень устали . Огромной вам всем удачи и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla
Упражнения
Упражнение №1
Начертите схему цепи, изображённой на рисунке 1, и объясните опыт, проведённый по данному рисунку.
Схема электрической цепи изображена на рисунке 2. Проводник обозначен прямоугольником.
Рисунок 2. Схема электрической цепи для проведенного опыта
В ходе этого опыта используют различные проводники. При этом фиксируют значения приборов. Сила тока изменяется в зависимости от того, какой проводник включен в цепь. Напряжение же на концах разных проводников все время остается постоянным.
Этот опыт доказывает связь силы тока и свойства проводника, называемого электрическим сопротивлением.
Упражнение №2
Выразите в омах значения следующих сопротивлений: $100 \space мОм$; $0.7 \space кОм$; $20 \space МОм$.
Дано: $I_1 = 100 \space мОм$ $I_2 = 0.7 \space кОм$ $I_3 = 20 \space МОм$
Показать решение и ответ
Скрыть
Решение:
$I_1 = 100 \space мОм = 100 \cdot 0.001 \space Ом = 0.1 \space Ом$, $I_2 = 0.7 \space кОм = 0.7 \cdot 1000 \space Ом = 700 \space Ом$, $I_3 = 20 \space МОм = 20 \cdot 1 \space 000 \space 000 \space Ом = 20 \space 000 \space 000 \space Ом$.
Ответ: $I_1 = 0.1 \space Ом$, $I_2 = 700 \space Ом$, $I_3 = 20 \space 000 \space 000 \space Ом$.
Ом
Все существующие материалы имеют физическую способность к проводимости электрического тока. Эти материалы подразделяются на 2 основные группы:
- Изоляторы. Подобные материалы не проводят электрический ток. Из наиболее известных изоляторов можно выделить резину, дерево, стекло, пластик.
- Проводники. Эти материалы имеют сравнительно маленькое сопротивление, поэтому свободно пропускают через себя заряженные электроны. В электротехнике используется медь, алюминий, железо, золото.
Ом — это в системе СИ единица измерения электрического сопротивления. Эта способность материалов была открыта немецким физиком Георгом Симоном Омом. Параметр проводимости получил свое специальное обозначение — значок Ома или символ Омега «Ω».
Физика в качестве базовой величины сопротивления использует величину 1 Ом. Сила в 1000 Ом имеет сокращенное обозначение 1 кОм. В зависимости от типа проводника, сопротивление может иметь различные значения. В физике максимальное значение сопротивление — 1 Йоттаом (ИОм), которое равняется 10 в 24 степени Ом. Сколько существует различных производных единиц сопротивления, можно увидеть на рисунке ниже.
По причине часто возникающих ошибок при написании, было принято еще одно обозначение Ом для Европейской системы классификации. Во многих технических руководствах вы можете встретить обозначение «ohm».
Важно! В рукописном варианте для обозначения сопротивления используют само слово «Ом», а не греческую букву «Омега». Знак «Ω» используется в электронных технических руководствах и при обозначении параметров радиодеталей.
Параметр проводимости измеряется не только по системе СИ. Существует система СГС, которая определяет проводимость по параметрам длины, веса и времени. Параметр СГС или сантиметр, грамм, секунда. По данной классификации, электрическая проводимость для СГС имеет обозначение СГСR. Величина указывает сопротивление не всего проводника, а только его отдельного участка, с учетом длины и веса. Также учитывается время прохождения заряда в 1 вольт по этому участку.
СГС и обычная электрическая проводимость сильно отличаются. Так одна единица СГСR равняется 9*10 в 11 степени Ом. Данная система не имеет практического применения в радиоэлектронике, по причине того, что многие расчетные величины безмерны. Она используется при расчетах электромагнетизма в системе Гаусса, а также в электродинамике.
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.
| Кратные | Дольные | ||||||
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Ом | декаом | даОм | daΩ | 10−1 Ом | дециом | дОм | dΩ |
| 102 Ом | гектоом | гОм | hΩ | 10−2 Ом | сантиом | сОм | cΩ |
| 103 Ом | килоом | кОм | kΩ | 10−3 Ом | миллиом | мОм | mΩ |
| 106 Ом | мегаом | МОм | MΩ | 10−6 Ом | микроом | мкОм | µΩ |
| 109 Ом | гигаом | ГОм | GΩ | 10−9 Ом | наноом | нОм | nΩ |
| 1012 Ом | тераом | ТОм | TΩ | 10−12 Ом | пикоом | пОм | pΩ |
| 1015 Ом | петаом | ПОм | PΩ | 10−15 Ом | фемтоом | фОм | fΩ |
| 1018 Ом | эксаом | ЭОм | EΩ | 10−18 Ом | аттоом | аОм | aΩ |
| 1021 Ом | зеттаом | ЗОм | ZΩ | 10−21 Ом | зептоом | зОм | zΩ |
| 1024 Ом | йоттаом | ИОм | YΩ | 10−24 Ом | йоктоом | иОм | yΩ |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Компенсационный метод
Его применяют для получения повышенной точности измерения. Ниже показана схема подобной установки:
В данную схему входит компенсатор постоянного тока, двухпозиционный переключатель (П2 и П1), резистор образцовый R0, а также источник питания Е и измеряемый резистор Rх. Измеряв падение напряжения на каждом из резисторов при двух разных положениях переключателя определяют – UR0=R0I и URХ=RХI. Из этих выражений можно получить следующую формулу:
При выполнении измерений необходимо ток I поддерживать постоянным и не допускать изменения его значения, для обеспечения точности измерения.