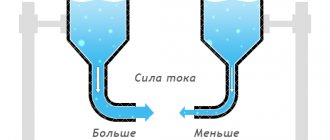
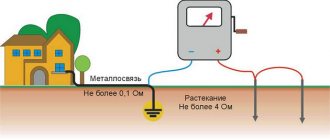
Зависимость показаний амперметра и вольтметра от используемого проводника в цепи
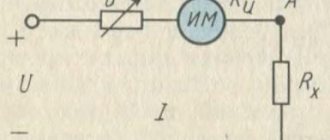
Для начала проведем интересный опыт. Соберем электрическую цепь из источника тока, ключа, амперметра и вольтметра. Также мы будем включать в эту цепь проводники из различных материалов. Они закреплены на специальной панели. К этим же проводникам мы будем параллельно подключать вольтметр (рисунок 1).
Проводники у нас обозначены следующим образом: AB — железная проволока, CD — никелиновая проволока, EF — медная проволока.
Эти проводники имеют одинаковую длину и сечение.
Рисунок 1. Зависимость силы тока от используемого в цепи проводника
Сначала подключим в цепь железную проволоку AB. Зафиксируем показания амперметра и вольтметра после замыкания ключа.
Теперь переключимся на никелиновую проволоку CD. Мы заметим, что сила тока в цепи уменьшилась.
Испробуем третий проводник: медную проволоку EF. Теперь сила тока значительно увеличилась.
Вы не забыли, что в нашем опыте был еще и вольтметр? Мы поочередно подключали его к каждому из проводников.
Каждый раз мы получали одинаковое значение напряжения. Оно не изменялось.
Использование веществ для изготовления проводников и изолятов
У каких веществ самые большие значения удельного сопротивления? Конечно, у диэлектриков. Например, эбонит и фарфор практически не проводят электрический ток. Поэтому их и используют в качестве изоляторов.
Самое меньшее удельное сопротивление имеют чистые металлы. Серебро и медь — лучшие проводники электричества.
Из каких веществ изготавливают проводники, применяемые на практике? Чаще всего для проводки электрических цепей используют медные, алюминиевые и железные провода.
В таблице 1 вы также могли обратить внимание на значения удельных сопротивлений для сплавов нескольких веществ. Они имеют достаточно большие значения. Зачем? Обычно их используют для изготовления приборов, которым необходимо для нормального функционирования иметь большое сопротивление, но все-таки пропускать ток.
Зависимость силы тока от свойств проводников
Вы уже знаете, что сила тока зависит от напряжения. Ведь напряжение является характеристикой электрического поля.
Но в нашем опыте напряжение оставалось постоянным. Значит, сила тока имеет еще одну зависимость.
Сила тока в цепи зависит от свойств проводников, включенных в электрическую цепь.
Значения удельных сопротивлений некоторых веществ
В таблице 1 приведены значения удельных сопротивлений некоторых веществ.
| Вещество | $\rho$, $\frac{Ом \cdot мм^2}{м}$ | Вещество | $\rho$, $\frac{Ом \cdot мм^2}{м}$ |
| Серебро | $0.016$ | Манганин (сплав) | $0.43$ |
| Медь | $0.017$ | Константан (сплав) | $0.50$ |
| Золото | $0.024$ | Ртуть | $0.96$ |
| Алюминий | $0.028$ | Нихром (сплав) | $1.1$ |
| Вольфрам | $0.055$ | Фехраль (сплав) | $1.3$ |
| Железо | $0.10$ | Графит | $13$ |
| Свинец | $0.21$ | Фарфор | $10^{19}$ |
| Никелин (сплав) | $0.40$ | Эбонит | $10^{20}$ |
Таблица 1. Удельное сопротивление некоторых веществ (при $t = 20 \space \degree C$)
Обратите внимание, что эти значения актуальны при температуре $20 \space \degree C$.
Удельное сопротивление вещества зависит от температуры.
Опыты показали, что при определенной температуре для каждого вещества диэлектрик может стать проводником (полупроводник). Также экспериментально доказано, что с повышением температуры удельное сопротивление металлов увеличивается.
Причины электрического сопротивления
В чем же причина сопротивления?
Вспомните урок «Электрический ток в металлах«. Электроны, двигаясь под действием электрического поля, обретают некоторое направление. Но при этом хаотичность их движения сохраняется. Мы еще сравнивали такое движение со стайкой мошкары, которую относит ветром.
Итак, электроны приведены в упорядоченное движение электрическим полем. При этом они взаимодействуют с ионами кристаллической решетки. Что при этом происходит? Упорядоченное движение замедляется. Теперь меньшее число электронов проходит через поперечное сечение проводника за $1 \space с$. Значит, уменьшается сила тока.
Сделаем вывод из наших рассуждений.
Причина сопротивления — это взаимосвязь движущихся электронов с ионами кристаллической решетки.
Логично, что разные проводники будут обладать разными значениями сопротивления. Все дело будет в различиях строения их кристаллической решетки. Кроме того, значение будут иметь длина проводника и площадь его поперечного сечения. Об этом мы поговорим в следующих уроках.
Результаты опытов
Какие выводы мы сможем сделать после всех расчетов?
- Из двух никелиновых проволок с одинаковой толщиной большее сопротивление имеет более длинная проволока
- Большее сопротивление имеет та никелиновая проволока, у которой поперечное сечение меньше. При этом длина проволок была одинаковой
- Никелиновая и нихромовая проволоки имеют разное сопротивление при одинаковых размерах
Упражнения
Упражнение №1
Начертите схему цепи, изображённой на рисунке 1, и объясните опыт, проведённый по данному рисунку.
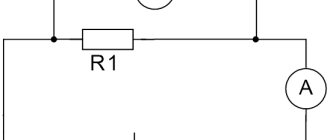
Схема электрической цепи изображена на рисунке 2. Проводник обозначен прямоугольником.
Рисунок 2. Схема электрической цепи для проведенного опыта
В ходе этого опыта используют различные проводники. При этом фиксируют значения приборов. Сила тока изменяется в зависимости от того, какой проводник включен в цепь. Напряжение же на концах разных проводников все время остается постоянным.
Этот опыт доказывает связь силы тока и свойства проводника, называемого электрическим сопротивлением.
Упражнение №2
Выразите в омах значения следующих сопротивлений: $100 \space мОм$; $0.7 \space кОм$; $20 \space МОм$.
Дано: $I_1 = 100 \space мОм$ $I_2 = 0.7 \space кОм$ $I_3 = 20 \space МОм$
Показать решение и ответ
Скрыть
Решение:
$I_1 = 100 \space мОм = 100 \cdot 0.001 \space Ом = 0.1 \space Ом$, $I_2 = 0.7 \space кОм = 0.7 \cdot 1000 \space Ом = 700 \space Ом$, $I_3 = 20 \space МОм = 20 \cdot 1 \space 000 \space 000 \space Ом = 20 \space 000 \space 000 \space Ом$.
Ответ: $I_1 = 0.1 \space Ом$, $I_2 = 700 \space Ом$, $I_3 = 20 \space 000 \space 000 \space Ом$.
Единица удельного сопротивления
Чтобы определить единицу измерения удельного сопротивления обратимся к формуле $\rho = \frac{RS}{l}$.
Единица сопротивления — $1 \space Ом$, площади поперечного сечения — $1 \space м^2$, длины — $1 \space м$.
Подставим все это в формулу:
$[\rho] = \frac{1 \space Ом \cdot 1 \space м^2}{1 \space м} = 1 \space Ом \cdot м$.
Площадь поперечного сечения проводника обычно небольшая, поэтому ее удобно выражать в $мм^2$. Поэтому часто удельное сопротивление проводника измеряют в $\frac{1 \space Ом \cdot 1 \space мм^2}{1 \space м}$.
Идеальный источник тока
Идеальный источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах. Предполагается, что внутреннее сопротивление идеального источника тока бесконечно велико , и поэтому параметры внешней электрической цепи, от которых зависит напряжение на зажимах источника, не влияют на ток источника. Условные обозначения идеального источника тока приведены на рис. 1
Стрелка в источнике тока или знаки «+» и «—» указывают положительное направление тока i(t)
или полярность источника, т. е. направление перемещения положительных зарядов.
Сейчас принято обозначать источники тока буквой J, и чаще всего применяется нижнее условно графическое изображение.
Идеальный источник тока
По мере неограниченного увеличения сопротивления внешней электрической цепи, присоединенной к идеальном
у источнику тока, напряжение на его зажимах и соответственно мощность, развиваемая им, неограниченно возрастают.Поэтому идеальный источник тока, так же как и идеальный источник напряжения, рассматривается как источник бесконечной мощности.
Источник тока конечной мощности изображается в виде идеального источника тока с параллельно подключенным к его зажимам пассивным элементом который характеризует внутренние параметры источника и
Представляя собой теоретическое понятие, источник тока применяется в ряде случаев для расчета электрических цепей.
Некоторым подобием источника тока может служить устройство, состоящее из аккумулятора, соединенного последовательно с дополнительным большим сопротивлением Другим примером источника тока может являться пяти электродная усилительная электронная лампа (пентод). Имея внутреннее сопротивление несоизмеримо большее, чем сопротивление внешней электрической цепи, эти устройства отдают ток, почти не зависящий от изменения внешней нагрузки в широких пределах, и именно в этом отношении они аналогичны источнику тока.
Почему проводник “сопротивляется”?
Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.
В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).
Таким образом возникает сопротивление протеканию (нарастанию) тока.
Рис. 1. Электрический ток в проводнике ограничивается столкновением электронов с атомами.
Измерение внутреннего сопротивления.
Существует несколько методик измерения внутреннего сопротивления. Две из них прописаны в ГОСТ Р МЭК 61960-2007. Перед замером любым из приведенных ниже методов аккумулятор должен быть полностью заряжен. Испытания проводятся при температуре 20±5ºC.
Измерение внутреннего сопротивления методом переменного тока (а.с.)
С помощью этого метода измеряется импеданс, который на частоте 1000 Гц приблизительно равен сопротивлению.
Электрический импеданс (комплексное электрическое сопротивление) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Описание методики из ГОСТ
В течение одной – пяти секунд измеряем среднеквадратичное значение переменного напряжения Urms, возникающего при прохождении через аккумулятор переменного тока со среднеквадратичным значением Irms , следующего с частотой 1000 Гц. Внутреннее сопротивление Ra.c., Ом рассчитываем по формуле Ra.c.= Urms / Irms .
Irms (rms – Root Mean Square – среднеквадратичное значение).
Переменный ток должен иметь такое значение, чтобы пиковое напряжение не превышало 20 мВ.
Этот метод сложно воплотить в домашних условиях без специального оборудования. Популярный прибор YR1035 отлично справляется с измерениями с точностью 0,01 мОм. Зарядные устройства SKYRC MC3000 ,Opus BT-C3100V2.2, Liitokala Lii-500 также измеряют методом АС, но весьма с посредственной точностью.
Измерение внутреннего сопротивления методом постоянного тока (d.c.)
Этот метод возможно выполнить в домашних условиях с помощью обычных вольтметра и амперметра и пары подходящих нагрузочных сопротивлений. В качестве сопротивлений вполне можно использовать несколько автомобильных ламп накаливания или импровизированный резистор из нихромовой проволоки.
Описание метода из ГОСТ
- Разряжаем аккумулятор постоянным током I1= 0,2 Iн. На десятой секунде измеряем значение напряжения U1 на клеммах аккумулятора.
- Увеличиваем разрядный ток до значения I2=Iн. На следующей секунде измеряем значение напряжения U2 на клеммах аккумулятора.
Внутреннее сопротивление Rd.c., Ом рассчитываем по формуле Rd.c. = (U1-U2)/(I2-I1)
- Iн – номинальный ток разряда аккумулятора.
Схема для измерения внутреннего сопротивления по методике постоянного тока (d.c.)
Сопротивление R1 и R2 подбирается таким образом, чтобы протекали токи I1 и I2 нужной величины. Ориентироваться нужно на номинальный разрядный ток аккумулятора.
Вольтметр необходимо подключать непосредственно на полюса источника, чтобы исключить влияние от падения напряжения на проводах .
Как правильно пользоваться мультиметром: инструкция для чайников
Рассмотрим, как измерить несколько электрических характеристик.
Потенциал
Алгоритм для определения напряжения:
- Установить режим в позицию ACV или DCV в предполагаемом интервале.
- Черный провод подключить к коннектору СОМ, красный — к разъему VΩmA.
- Наконечники щупов соединить с контактами цепи. Например, ввести в отверстия розетки или на полюса батарейки.
- Провести измерение.
Высветившееся на дисплее число — величина напряжения в вольтах. Знак «минус» говорит о том, что полярность была нарушена. Если мультиметр поддерживает функцию удержания, значение можно зафиксировать кнопкой HOLD. Это удобно для большой цепочки измерений.
Сила тока
Эта характеристика измеряется только при последовательном подключении тестера в цепь и включенном питании. Большинство приборов дают возможность определить силу тока до 10 А, поскольку в быту большие значения используются редко. Для проведения измерений в цепи устраивается разрыв. Дальнейшие действия по следующей схеме:
- Черный щуп — в гнездо СОМ.
- Красный — в разъем до 200 мА или 10А.
- Наконечниками осторожно прикоснуться к контактам.
- Считать с дисплея значение напряжения.
При работе с оголенными проводами необходимо соблюдать технику безопасности, чтобы не допустить удара током.
Сопротивление
Эту характеристику можно измерить без подачи питания. Исследуемый элемент просто замыкается между двумя щупами. Если проводимости нет, на экране высвечивается единица. Последовательность действий:
- Установить режим Ω, выбрав максимальный диапазон.
- Щупы вставить в соответствующие коннекторы.
- Проверить состояние — замкнуть щупы друг на друга. Должен появиться 0 или небольшое число, которое нужно учитывать при измерении сопротивления цепи.
- Концы проводников набросить на контакты исследуемого объекта.
- На экране появится сопротивление элемента или участка цепи.
Для точных измерений рекомендуется провести 2-3 попытки.
Комплексный анализ
Для схемы резистора и конденсатора в последовательном соединении источник переменного тока указывается как:
Последовательность RC
vin (t) = Vejωt (V – амплитуда переменного напряжения, j – мнимая единица (j2 = -1), а ω – угловая частота источника переменного тока).
Важно отметить два момента:
- Мы используем строчный алфавит для напряжения источников, чтобы разобраться в том, как они чередуются.
- Мнимая единица отображается как «j».
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Будет интересно➡ Индуктивное сопротивление
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
Формула закона Ома
Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:
\[E=IR\]
В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:
\
\