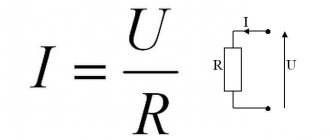Ohm's law for a closed circuit shows that the current value in a real circuit depends not only on the load resistance, but also on the source resistance.
The formulation of Ohm's law for a closed circuit is as follows: the amount of current in a closed circuit consisting of a current source with internal and external load resistances is equal to the ratio of the electromotive force of the source to the sum of the internal and external resistances.
For the first time, the dependence of current on resistance was experimentally established and described by Georg Ohm in 1826.
The formula for Ohm's law for a closed circuit is written as follows:
Where:
- I [A] – current strength in the circuit,
- ε [V] – EMF of the voltage source,
- R [Ohm] – resistance of all external elements of the circuit,
- r [Ohm] – internal resistance of the voltage source
Original and modern formulation
This seemingly simple law was formulated by the German physicist Georg Ohm in 1826. He published the corresponding scientific article the following year.
It is interesting to note that the appearance of this work did not cause a stir. The scientific community appreciated Ohm's discovery only after the publication of works by the physicist Poulier of similar content in 1830. In 1833 Ohm received his doctorate from the University of Nuremberg. In 1872, the unit of resistance became known as the Ohm. In its simplest form, the law for a section of a chain sounds like this:
The law is empirical in nature, since it expresses a generalized analysis of a large amount of experimental data.
Now the formula for Ohm's law for a complete electrical circuit is as follows:
I = ℰ / (R+r).
Here:
- ℰ — EMF of the voltage source, V;
- I is the current strength in the circuit, A.
- R is the total resistance of all external elements of the circuit, Ohm;
- r is the internal resistance of the voltage source, Ohm.
Ohm's law for a complete circuit takes into account the total resistance, which is the sum of the circuit resistance R and the internal resistance of the current source r.
Georg Ohm originally formulated it differently. Ohm's law for a closed circuit looked like this:
X = a / ( b + l ), where
- a is a quantity characterizing the current source. Now they say that this is the electromotive force of the current source;
- b represents a property of the electrical installation, which is now considered as the internal resistance of the current source;
- l is a value that depends on the length of the wires used (in modern terms, it corresponds to the resistance of the electrical circuit).
As you can see, Ohm's law, applied to a complete electrical circuit, has the same formulation in both versions.
Ohm's law in differential form is also applied. In this case, very small quantities are considered. But this allows the use of integral and differential calculus for complex cases.
Joule-Lenz law
The Joule-Lenz law states: the amount of heat released in a conductor in a section of an electrical circuit with resistance $R$ when a direct current $I$ flows through it for a time $t$ is equal to the product of the square of the current and the resistance and time:
$Q=I^2Rt$
The law was established in 1841 by the English physicist J. P. Joule, and in 1842 it was confirmed by the precise experiments of the Russian scientist E. H. Lenz. The very phenomenon of heating a conductor when current passes through it was discovered back in 1800 by the French scientist A. Fourcroy, who managed to heat an iron spiral by passing an electric current through it.
From the Joule-Lenz law it follows that when conductors are connected in series, since the current in the circuit is the same everywhere, the maximum amount of heat will be released on the conductor with the greatest resistance. This is used in technology, for example, for spraying metals.
In a parallel connection, all conductors are under the same voltage, but the currents in them are different. From the formula ($Q=I^2Rt$) it follows that, since, according to Ohm’s law, $I={U}/{R}$, then
$Q={U^2t}/{R}$
Therefore, more heat will be generated on a conductor with less resistance.
If in the formula ($A=IUt$) we express $U$ in terms of $IR$, using Ohm's law, we obtain the Joule-Lenz law. This once again confirms the fact that the work of the current is spent on heat generation at the active resistance in the circuit.
Practical use
In most cases, the internal resistance of the current source is considered to be relatively small compared to that found in the electrical circuit. In this case, Ohm's law for a closed circuit is applied in an abbreviated formulation: I = U / R.
To better understand what physical processes occur in an electrical circuit, you need to consider the following:
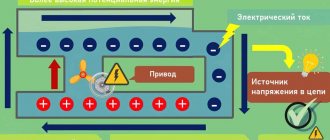
- Processes are observed in the current source that lead to the formation of a potential difference at the terminals. When an electrical circuit is connected to them, current flows through it. It is generally accepted that it passes from a positive potential to a negative one.
- Current is the ordered movement of electrons. The substance contains a huge number of these particles, which move at high speed from negative to positive potential.
- The speed of electrons depends on the material of the conductor through which they pass, on its cross-section and length. If the latter is doubled, it will double the resistance.
Resistors are used in an electrical circuit in cases where a strictly defined resistance is required for the operation of the device. If the terminals of the current source, in simple words, are connected directly, then the resistance will be small and the current will be relatively large. On the one hand, high current in some cases can melt the wire; on the other hand, it leads to accelerated battery discharge.
In matter, the movement of electrons is not free. When moving, particles must overcome resistance, expending their energy to do so. The amount of resistance depends on the specific material. In conductors, electrons move relatively easily. No current can pass through insulators unless a voltage so high is applied that the situation creates a breakdown.
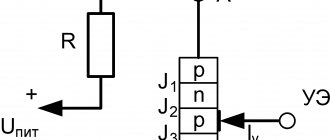
Semiconductors undergo more complex processes because they have a rigid crystal structure. In the presence of certain types of impurities, electron or hole conductivity can occur. Current can represent the movement of both electrons and holes.
A more accurate resistance characteristic can be obtained from the following formula:
Using resistivity, you can characterize the electrical properties of a certain substance. This value represents the resistance that a piece of wire made of this material has a length of 1 m and a cross-sectional area of 1 sq. m. mm.
Parallel and serial connection
In electrics, elements are connected either in series - one after the other, or in parallel - this is when several inputs are connected to one point, and outputs from the same elements are connected to another.
Ohm's law for parallel and series connections
Serial connection
How does Ohm's law work for these cases? With a series connection, the current flowing through the chain of elements will be the same. The voltage of a section of a circuit with elements connected in series is calculated as the sum of the voltages in each section. How can this be explained? The flow of current through an element is the transfer of part of the charge from one part to another. That is, this is a certain job. The amount of this work is tension. This is the physical meaning of tension. If this is clear, let's move on.
Serial connection and parameters of this section of the circuit
With a series connection, the charge has to be transferred through each element in turn. And on each element this is a certain “amount” of work. And to find the amount of work on the entire section of the chain, you need to add up the work on each element. So it turns out that the total voltage is the sum of the voltages on each of the elements.
In the same way - using addition - the total resistance of a circuit section is found. How can you imagine this? Current flowing through a chain of elements consistently overcomes all resistance. One after another. That is, to find the resistance that he overcame, you need to add up the resistances. Like that. The mathematical derivation is more complex, but it is easier to understand the mechanism of action of this law.
Parallel connection
A parallel connection is when the beginnings of the conductors/elements converge at one point, and their ends are connected at another. We will try to explain the laws that are valid for compounds of this type. Let's start with the current. A current of some magnitude is supplied to the point of connection of the elements. It separates, flowing through all conductors. From here we conclude that the total current in the section is equal to the sum of the current on each of the elements: I = I1 + I2 + I3.
Now regarding the voltage. If voltage is the work done to move a charge, then the work required to move one charge will be the same on any element. That is, the voltage on each parallel-connected element will be the same. U = U1=U2=U3. It’s not as fun and visual as in the case of explaining Ohm’s law for a section of a circuit, but you can understand it.
Laws for parallel connection
For resistance, everything is a little more complicated. Let's introduce the concept of conductivity. This is a characteristic that shows how easy or difficult it is for a charge to pass through this conductor. It is clear that the lower the resistance, the easier it will be for current to pass. Therefore, conductivity - G - is calculated as the reciprocal of resistance. In the formula it looks like this: G = 1/R.
Why did we talk about conductivity? Because the total conductivity of a section with a parallel connection of elements is equal to the sum of the conductivity for each of the sections. G = G1 + G2 + G3 - easy to understand. How easy it is for current to cross this node of parallel elements depends on the conductivity of each element. So it turns out that they need to be folded.
Now we can move on to resistance. Since conductivity is the reciprocal of resistance, we can obtain the following formula: 1/R = 1/R1 + 1/R2 + 1/R3.
What does parallel and serial connection give us?
Theoretical knowledge is good, but how to apply it in practice? Elements of any type can be connected in parallel or in series. But we considered only the simplest formulas describing linear elements. Linear elements are resistances, which are also called “resistors”. So here's how you can use what you've learned:
- If there is no large resistor available, but there are several smaller ones, the required resistance can be obtained by connecting several resistors in series. As you can see, this is a useful technique.
- To extend the life of the batteries, they can be connected in parallel. In this case, according to Ohm’s law, the voltage will remain the same (you can verify this by measuring the voltage with a multimeter). And the “lifetime” of a dual battery will be significantly longer than that of two elements that replace each other. Just note: only power supplies with the same potential can be connected in parallel. That is, you cannot connect dead and new batteries. If you do connect, the battery that has a higher charge will tend to charge the less charged one. As a result, their total charge will drop to a low value.
Practical application of Ohm's law: you can create power supplies with the desired voltage and current
In general, these are the most common uses for these compounds.
Integral and differential forms of the law
All of the above points with calculations are applicable to conditions when conductors of, so to speak, “homogeneous” structure are used in electrical circuits. Meanwhile, in practice, one often has to deal with the construction of schematics, where the structure of the conductors changes in different sections. For example, wires of a larger cross-section or, conversely, a smaller one, made from different materials, are used. To take into account such differences, there is a variation of the so-called “differential-integral Ohm’s law.” For an infinitesimal conductor, the current density level is calculated depending on the voltage and conductivity value.
For the differential calculation, the formula is taken: J = ό * E. For the integral calculation, accordingly, the formulation is: I * R = φ1 – φ2 + έ However, these examples are rather closer to the school of higher mathematics and are not actually used in the real practice of a simple electrician.
Sources
- https://tel-spb.ru/ohm/
- https://elektroznatok.ru/info/teoriya/zakon-oma
- https://ElectroInfo.net/teorija/vse-o-zakone-oma-prostymi-slovami-s-primerami-dlja-chajnikov.html
- https://radioprog.ru/post/920
- https://YDoma.info/ehlektrotekhnika/electricity-zakon-oma.html
- https://toe.1c-umi.ru/lekcii/lekciya_6_-_zakon_oma/
[collapse]
Current source resistance
Ohm's law for a complete electrical circuit and formulas for calculating its parameters characterize not only the current passing through the circuit, but also that which exists inside the current source. Ohm's law for a section of a circuit does not take into account the presence of this quantity.
The battery is responsible for the movement of electrons from the positive terminal to the negative terminal. Through an electrical circuit they are constantly moving in the opposite direction. The decrease in their number on the negative terminal and the excess on the positive terminal are constantly compensated by processes occurring inside the device.
This movement of electrons is also an electric current. In this case, the particles have to overcome the internal resistance of the current source. As the temperature increases, the resistance may change, the nature of the change depends on the specific material.
Coulomb and electric charge
One of the basic units of electrical measurement that is often taught early in electronics courses but not often used subsequently is the coulomb, a unit of electrical charge proportional to the number of electrons in an unbalanced state. One coulomb of charge corresponds to 6,250,000,000,000,000,000 electrons. The symbol for the amount of electric charge is the capital letter "Q", and the unit of coulombs is denoted "C". The unit of current, ampere, is equal to 1 coulomb of charge passing through a given point in a circuit in 1 second. In this sense, current is the speed at which an electric charge moves through a conductor.
As stated earlier, voltage is a measure of the potential energy per unit of charge available to stimulate the flow of current from one point to another. Before we can define exactly what a "volt" is, we must understand how to measure this quantity, which we call "potential energy." The common metric unit for measuring energy of any kind is the joule, which is equal to the amount of work done by a force of 1 newton when moving 1 meter (in the same direction). In these scientific terms, 1 volt is equal to 1 joule of electrical potential energy per (divided by) 1 coulomb of charge. Thus, a 9-volt battery releases 9 joules of energy for every coulomb of charge passing through the circuit.
These units and symbols for electrical quantities will become very important when we begin to explore the relationships between them in circuits.
Empirical nature of Ohm's law
When studying the nature of electricity through scientific research, certain laws are formulated. They differ from each other not only in their content, but also in how they were derived. Some laws are a consequence of more general statements, others are a successful attempt to explain repeatedly observed facts.
Ohm's law for a homogeneous area is actually an attempt to create a rule that fits a large number of observations and experiments. Its formulation has been confirmed in practice over the centuries, acquiring the force of a fundamental law of physics. Ohm's law, presented in integral form, makes it possible to perform calculations for various electrical circuits.
Properties of electric current
The direction of electric current is considered to be the movement of free positive charges. A current is called constant if its direction and strength are constant over time.
An electric field of magnitude E acts on a charge of magnitude q with a force F, which is equal to:
$F = q * E$ (1).
As a result, an electric current arises in the conductor. To create an electric field E, a voltage U must be applied to the ends of the conductor, which is equal to the potential difference φ1 and φ2 at the ends of the conductor:
$ U = φ2 – φ1 $ (2),
in this case φ2 > φ1.
The unit of electric current, the ampere (A), is named after the French physicist Ampere. This unit is one of the seven basic units in the International System of Units. The unit of measurement for voltage is the volt (V), named after the Italian explorer Alessandro Volta.
Use for AC
As is known, in an alternating current circuit there is both active and reactive resistance. The first of them coincides with how this quantity was understood in the time of Georg Ohm. However, inductive and capacitive reactance also inhibit the movement of electrons. In this case, Ohm's law for alternating current applies.
To use this law in such circuits, instead of ohmic resistance, total resistance should be considered, which takes into account the total effect of the active and reactive components of the resistance.
In the presented circuit, the total resistance is denoted as Z. Ohmic, inductive and capacitive - R, XL and XC, respectively. Ohm's law for an alternating current circuit takes into account all these variations. The calculation formula implies that the addition of resistances occurs according to the vector rule.
To determine all resistances, a right triangle is used, one leg of which expresses the active resistance, and the second - the reactive one. The latter is equal to the difference between inductive and capacitive reactances. The determination of the total is carried out according to the Pythagorean theorem, according to which the length of the hypotenuse is equal to the square root of the sum of the squares of the legs.
Energy balance on a chain section
If external forces act on a section of the chain, then we should talk about three terms in the energy balance:
1) To find the amount of heat released, it is necessary to calculate the work of the total field on the charges of the circuit. As stated by the generalized Ohm's law, the work of the total field on a unit charge is equal to I
12
R
means that during time
t
the total field will do the work
\(~Q = I_{12} Rq = I_{12} R(I_{12} t) = I^2_{12} Rt\)
(Joule-Lenz law) . This value is always positive.
2) The work of external forces on charges should be interpreted as the supply of energy from non-electrostatic energy sources. It is equal
\(~A_{st} = \varepsilon_{12} q = \varepsilon_{12} I_{12} t\) .
This value can be either positive or negative.
3) The work of electrostatic forces on charges is equal to
\(~A_{el} = (\varphi_1 — \varphi_2)q = U_{12} I_{12} t\) .
To understand the energy meaning of this expression, we note that, in accordance with Ohm’s generalized law,
\(~I_{12}Rq = (\varphi_1 - \varphi_2 + \varepsilon_{12}) q\) .
or
\(~Q = A_{el} + A_{st}\) .
This means, based on the law of conservation of energy, it can be argued that the work of electrostatic forces on a section of the circuit is equal to the energy received in this section from the rest of the circuit (i.e. from the external circuit)
.
If this work is negative, then in the external circuit the work of electrostatic forces is positive, i.e. UI
has a meaning of energy transferred to the external circuit. Thus, electrostatic forces regulate the exchange of energy between parts of the circuit.
Let's discuss two examples.
Rice. 5
Current source efficiency
To calculate the efficiency, you need to figure out which value in this particular case plays the role of total (expended) work, and which value plays the role of useful work.
Let's consider a situation where the current source is the source of energy for an external circuit (containing, for example, an ideal resistor that only generates heat). In this case (Fig. 5, a) external forces of the source perform positive work \(~A_{st} = \varepsilon It\), which has the meaning of total (expended) work, part of the energy \(~Q = I^2 rt\ ) is lost in the source in the form of heat, and part \(~A_{polezn} = (\varepsilon I - I^2 r)t = UIt\) is transferred to the external circuit. Electrostatic forces in the source itself perform negative work, and in the external circuit - positive work.
Electric motor efficiency
Let us now consider the case when a section of the circuit receives energy from an external circuit, and this energy is not converted entirely into heat, but is partially used to perform work. This is only possible when there are external forces in the area (in an ideal resistor, all the energy turns into heat). These external forces act against the current, doing negative work (Fig. 5, b), and the work against external forces is positive.
ε occurs in the windings of a rotating armature
. In this case, the positive work of electrostatic forces \(~A_{el} = UIt\) has the meaning of total (expended) work, part of the energy \(~Q = I^2 Rt\) is lost in the form of heat, and part \(~A_ {polezn} = (UI - I^2R)t = \varepsilon It\) represents useful work - the mechanical work of an electric motor.
Similar relationships can be written in many other cases (for example, when charging a battery).
Application in practice
When you need to work with an electrical circuit, it is important to know the voltage, current, resistance in the entire circuit or in individual sections. If two of these quantities are known, then using Georg Ohm's law you can find out the third without making direct measurements.
Sometimes it is necessary to use Ohm's law for a non-uniform section of a circuit. In this case, it is divided into separate zones and calculations are first carried out for them.
Since thermal or chemical effects depend on electrical parameters, applying Ohm's law you can calculate the possible effect. In particular, knowledge of such features allows you to avoid the destructive effect of too high a current.
Ohm's law can be expressed in integral and differential forms. In the first case, we are talking about the traditional formulation, and its expression in differential form takes into account specific conductivity - the reciprocal of resistivity.
In conclusion, it should be said that resistance measurement is carried out using a special device - an ohmmeter. But this is impossible to do in a working circuit. You can determine the resistance value without disconnecting the circuit by calculation using Ohm's law and by first measuring the voltage and current in the desired section of the circuit.
Nonlinear elements and circuits
Ohm's law is not a fundamental law of nature and can be applied in limited cases, for example, for most conductors. It cannot be used to calculate voltage and current in semiconductor or vacuum devices, where this dependence is not proportional and can only be determined using the current-voltage characteristic (volt-ampere characteristic). This category of elements includes all semiconductor devices (diodes, transistors, zener diodes, thyristors, varicaps, etc.) and vacuum tubes. Such elements and the circuits in which they are used are called nonlinear.
Similar articles: Direct current. Alternating current.
Comments and suggestions are accepted and welcome!
Full circuit formulation
The interpretation for a complete circuit will be slightly different than for a section, since the law compiled by Ohm also takes into account the parameter “r”, this is the resistance of the EMF source. The figure below illustrates such a diagram.
Circuit with source connected
Taking into account “r” EMF, the formula will appear as follows:
Note that if “R” is made equal to 0, then it becomes possible to calculate the “I” that occurs during a short circuit.
The voltage will be less than the EMF, it can be determined by the formula:
Actually, the voltage drop is characterized by the parameter “I*r”. This property is characteristic of many galvanic power supplies.
Accepted units of measurement
It must be taken into account that all calculations must be carried out in the following units of measurement:
- voltage – in volts;
- current in amperes
- resistance in ohms.
If you come across other quantities, they will need to be converted to generally accepted ones.
Current strength I
Let a current flow in some conductor. That is, there is a directed movement of charged particles - for example, these are electrons. Each electron has an elementary electric charge (e= -1.60217662 × 10-19 Coulombs). In this case, a specific electric charge equal to the sum of all charges of flowing electrons will pass through a certain surface in a certain period of time.
The ratio of charge to time is called current strength. The more charge passes through a conductor in a certain time, the greater the current. Current strength is measured in Amperes.
Voltage U, or potential difference
This is exactly the thing that makes electrons move. Electric potential characterizes the ability of a field to do work to transfer charge from one point to another. So, between two points of a conductor there is a potential difference, and the electric field does work to transfer charge.
A physical quantity equal to the work of the effective electric field during the transfer of electric charge is called voltage. Measured in Volts. One Volt is the voltage that, when moving a charge of 1 C, does work equal to 1 Joule.
Resistance R
Current, as we know, flows in a conductor. Let it be some kind of wire. Moving along a wire under the influence of a field, electrons collide with atoms of the wire, the conductor heats up, and the atoms in the crystal lattice begin to vibrate, creating even more problems for the electrons to move. This phenomenon is called resistance. It depends on temperature, material, conductor cross-section and is measured in Ohms.
Monument to Georg Simon Ohm