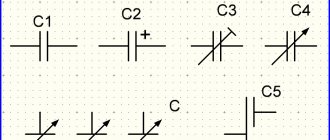В процессе проектирования электрической проводки, необходимо провести точные расчеты потери напряжения в кабеле. Это позволяет предотвратить сильное нагревание поверхности проводов в процессе эксплуатации. Благодаря этим мерам удаётся избежать появления короткого замыкания и преждевременной поломки бытовых приборов.
Помимо этого, формула позволяет правильно подобрать диаметр сечения провода, который подойдет для разного вида электромонтажных работ. Неправильный выбор, может стать причиной поломки всей системы. Облегчить поставленную задачу помогает онлайн – расчет.
Падение напряжения на проводе
Статья будет конкретная, с теоретическими выкладками и формулами. Кому не интересно, что откуда и почему, советую перейти сразу к Таблице 2 – Выбор сечения провода в зависимости от тока и падения напряжения.
И ещё – расчет потерь напряжения на длинной мощной трехфазной кабельной линии. Пример расчета реальной линии.
Итак, если взять неизменной мощность, то при понижении напряжения ток должен возрастать, согласно формуле:
P = I U. (1)
При этом падение напряжения на проводе (потери в проводах) за счет сопротивления рассчитывается, исходя из закона Ома:
U = R I. (2)
Из этих двух формул видно, что при понижении питающего напряжения потери на проводе возрастают. Поэтому чем ниже питающее напряжение, тем большее сечение провода нужно использовать, чтобы передать ту же мощность.
Для постоянного тока, где используется низкое напряжение, приходится тщательно подходить к вопросу сечения и длины, поскольку именно от этих двух параметров зависит, сколько вольт пропадёт зря.
Способы уменьшения потерь в электрических сетях
Пользователь сети не может повлиять на потери в ЛЭП, но может снизить падение напряжения на участке цепи, грамотно подключив ее элементы.
Медный кабель лучше соединять с медным, а алюминиевый — с алюминиевым. Количество соединений проводов, где материал жилы изменяется, лучше свести к минимуму, так как в таких местах не только рассеивается энергия, но и увеличивается тепловыделение, что при недостаточном уровне теплозоляции может быть пожароопасным. Учитывая показатели удельной проводимости и удельного сопротивления меди и алюминия, более эффективно в плане энергозатрат использовать медь.
Если это возможно, при планировании электрической цепи любые индуктивные элементы, такие как катушки (L), трансформаторы и электродвигатели, лучше подключать параллельно, так как согласно законам физики, общая индуктивность такой схемы снижается, а при последовательном подключении, наоборот, увеличивается.
Еще для сглаживания реактивной составляющей используют конденсаторные установки (или RC-фильтры в совокупности с резисторами).
В зависимости от принципа подключения конденсаторов и потребителя имеется несколько типов компенсации: личная, групповая и общая.
- При личной компенсации емкости присоединяют непосредственно к месту появления реактивной мощности, то есть собственный конденсатор — к асинхронному мотору, еще один — к газоразрядной лампе, еще один — к сварочному, еще один — для трансформатора и т.д. В этой точке приходящие кабели разгружаются от реактивных токов к отдельному пользователю.
- Групповая компенсация включает в себя присоединение одного или нескольких конденсаторов к нескольким элементам с большими индуктивными характеристиками. В данной ситуации регулярная одновременная деятельность нескольких потребителей связана с передачей суммарной реактивной энергии между нагрузками и конденсаторами. Линия, которая подводит электрическую энергию к группе нагрузок, разгрузится.
- Общая компенсация предусматривает вставку конденсаторов с регулятором в основном щите, или ГРЩ. Он производит оценку по факту текущего потребления реактивной мощности и быстро подсоединяет и отсоединяет нужное число конденсаторов. В результате берущаяся от сети общая мощность приводится к минимуму в согласии с моментальной величиной необходимой реактивной мощности.
- Все установки компенсации реактивной мощности включают в себя пару ветвей конденсаторов, пару ступеней, которые образуются специально для электрической сети в зависимости от потенциальных нагрузок. Типичные габариты ступеней: 5; 10; 20; 30; 50; 7,5; 12,5; 25 квар.
Для приобретения больших ступеней (100 и больше квар) соединяют параллельно небольшие. Нагрузки на сети уменьшаются, токи включения и их помехи снижаются. В сетях с множеством высоких гармоник сетевого напряжения конденсаторы защищают дросселями.
Автоматические компенсаторы обеспечивают сети, снабженной ими, такие преимущества:
- уменьшают загрузку трансформаторов;
- делают более простыми требования к сечению кабелей;
- дают возможность загрузить электросети больше, чем можно без компенсации;
- ликвидируют причины уменьшения напряжения сети, даже когда нагрузка подсоединена протяженными кабелями;
- увеличивают КПД мобильных генераторов на топливе;
- упрощают запуск электрических двигателей;
- увеличивают косинус фи;
- ликвидируют реактивную мощность из контуров;
- защищают от перенапряжений;
- совершенствуют регулировку характеристик сетей.
Сопротивление медного провода постоянному току
Сопротивление провода зависит от удельного сопротивления ρ, которое измеряется в Ом·мм²/м. Величина удельного сопротивления определяет сопротивление отрезка провода длиной 1 м и сечением 1 мм².
Сопротивление того же куска медного провода длиной 1 м рассчитывается по формуле:
R = (ρ l) / S, где (3)
R – сопротивление провода, Ом,
ρ – удельное сопротивление провода, Ом·мм²/м,
l – длина провода, м,
S – площадь поперечного сечения, мм².
Сопротивление медного провода равно 0,0175 Ом·мм²/м, это значение будем дальше использовать при расчетах.
Не факт, что производители медного кабеля используют чистую медь “0,0175 пробы”, поэтому на практике всегда сечение берется с запасом, а от перегрузки провода используют защитные автоматы, тоже с запасом.
Из формулы (3) следует, что для отрезка медного провода сечением 1 мм² и длиной 1 м сопротивление будет 0,0175 Ом. Для длины 1 км – 17,5 Ом. Но это только теория, на практике всё хуже.
Ниже приведу табличку, рассчитанную по формуле (3), в которой приводится сопротивление медного провода для разных площадей сечения.
Таблица 0. Сопротивление медного провода в зависимости от площади сечения
| S, мм² | 0,5 | 0,75 | 1 | 1,5 | 2,5 | 4 | 6 | 10 |
| R для 1м | 0,035 | 0,023333 | 0,0175 | 0,011667 | 0,007 | 0,004375 | 0,002917 | 0,00175 |
| R для 100м | 3,5 | 2,333333 | 1,75 | 1,166667 | 0,7 | 0,4375 | 0,291667 | 0,175 |
Потенциал
Напряженность электрического поля характеризует его силовые свойства. Для количественной характеристики энергетических возможностей поля было введено понятие потенциала. Потенциал электростатического поля φ — это отношение потенциальной энергии Wp заряда в поле к величине заряда q:
$ φ = {Wp\over {q * U}} $ (3).
Тогда напряжение между двумя точками электрической цепи (1-ой и 2-ой) можно выразить так:
$ U = φ_1 – φ_2 $ (4).
То есть становится более понятным физический смысл величины напряжения — это разность потенциалов в начальной точке 1 и конечной точке 2.
Для понимания смыслового значения напряжения можно воспользоваться аналогией с гравитационным полем, которое тоже является потенциальным. Масса тела m аналогична величине заряда q, а высота h, с которой может упасть, например, камень или поток воды, вращающий турбину, аналогична напряжению U. Напомним выражение для потенциальной энергии тела массы m в гравитационном поле Земли:
$ Е_p = m * g * h $ (5),
где: g — ускорение свободного падения, 9,8 м/с2. Видно, что формулы (2) и (4), полученные для разных потенциальных полей, очень похожи.
Расчет падения напряжения на проводе для постоянного тока
Теперь по формуле (2) рассчитаем падение напряжения на проводе:
U = ((ρ l) / S) I , (4)
То есть, это то напряжение, которое упадёт на проводе заданного сечения и длины при определённом токе.
Вот такие табличные данные будут для длины 1 м и тока 1А:
Таблица 1. Падение напряжения на медном проводе 1 м разного сечения и токе 1А:
| S, мм² | 0,5 | 0,75 | 1 | 1,5 | 2,5 | 4 | 6 | 8 | 10 |
| U, B | 0,0350 | 0,0233 | 0,0175 | 0,0117 | 0,0070 | 0,0044 | 0,0029 | 0,0022 | 0,0018 |
Эта таблица не очень информативна, удобнее знать падение напряжения для разных токов и сечений. Напоминаю, что расчеты по выбору сечения провода для постоянного тока проводятся по формуле (4).
Таблица 2. Падение напряжения при разном сечении провода (верхняя строка) и токе (левый столбец). Длина = 1 метр
| S,мм² I,A | 1 | 1,5 | 2,5 | 4 | 6 | 10 | 16 | 25 |
| 1 | 0,0175 | 0,0117 | 0,0070 | 0,0044 | 0,0029 | 0,0018 | 0,0011 | 0,0007 |
| 2 | 0,0350 | 0,0233 | 0,0140 | 0,0088 | 0,0058 | 0,0035 | 0,0022 | 0,0014 |
| 3 | 0,0525 | 0,0350 | 0,0210 | 0,0131 | 0,0088 | 0,0053 | 0,0033 | 0,0021 |
| 4 | 0,0700 | 0,0467 | 0,0280 | 0,0175 | 0,0117 | 0,0070 | 0,0044 | 0,0028 |
| 5 | 0,0875 | 0,0583 | 0,0350 | 0,0219 | 0,0146 | 0,0088 | 0,0055 | 0,0035 |
| 6 | 0,1050 | 0,0700 | 0,0420 | 0,0263 | 0,0175 | 0,0105 | 0,0066 | 0,0042 |
| 7 | 0,1225 | 0,0817 | 0,0490 | 0,0306 | 0,0204 | 0,0123 | 0,0077 | 0,0049 |
| 8 | 0,1400 | 0,0933 | 0,0560 | 0,0350 | 0,0233 | 0,0140 | 0,0088 | 0,0056 |
| 9 | 0,1575 | 0,1050 | 0,0630 | 0,0394 | 0,0263 | 0,0158 | 0,0098 | 0,0063 |
| 10 | 0,1750 | 0,1167 | 0,0700 | 0,0438 | 0,0292 | 0,0175 | 0,0109 | 0,0070 |
| 15 | 0,2625 | 0,1750 | 0,1050 | 0,0656 | 0,0438 | 0,0263 | 0,0164 | 0,0105 |
| 20 | 0,3500 | 0,2333 | 0,1400 | 0,0875 | 0,0583 | 0,0350 | 0,0219 | 0,0140 |
| 25 | 0,4375 | 0,2917 | 0,1750 | 0,1094 | 0,0729 | 0,0438 | 0,0273 | 0,0175 |
| 30 | 0,5250 | 0,3500 | 0,2100 | 0,1313 | 0,0875 | 0,0525 | 0,0328 | 0,0210 |
| 35 | 0,6125 | 0,4083 | 0,2450 | 0,1531 | 0,1021 | 0,0613 | 0,0383 | 0,0245 |
| 50 | 0,8750 | 0,5833 | 0,3500 | 0,2188 | 0,1458 | 0,0875 | 0,0547 | 0,0350 |
| 100 | 1,7500 | 1,1667 | 0,7000 | 0,4375 | 0,2917 | 0,1750 | 0,1094 | 0,0700 |
Какие пояснения можно сделать для этой таблицы?
1. Красным цветом я отметил те случаи, когда провод будет перегреваться, то есть ток будет выше максимально допустимого для данного сечения. Пользовался таблицей, приведенной у меня на СамЭлектрике: Выбор площади сечения провода.
2. Синий цвет – когда применение слишком толстого провода экономически и технически нецелесообразно и дорого. За порог взял падение менее 1 В на длине 100 м.
Как пользоваться таблицей выбора сечения?
Пользоваться таблицей 2 очень просто. Например, нужно запитать некое устройство током 10А и постоянным напряжением 12В. Длина линии – 5 м. На выходе блока питания можем установить напряжение 12,5 В, следовательно, максимальное падение – 0,5В.
В наличии – провод сечением 1,5 квадрата. Что видим из таблицы? На 5 метрах при токе 10 А потеряем 0,1167 В х 5м = 0,58 В. Вроде бы подходит, учитывая, что большинство потребителей терпит отклонение +-10%.
Но. ПрОвода ведь у нас фактически два, плюс и минус, эти два провода образуют кабель, на котором и падает напряжение питания нагрузки. И так как общая длина – 10 метров, то падение будет на самом деле 0,58+0,58=1,16 В.
Иначе говоря, при таком раскладе на выходе БП 12,5 Вольт, а на входе устройства – 11,34. Этот пример актуален для питания светодиодной ленты.
И это – не учитывая переходное сопротивление контактов и неидеальность провода (“проба” меди не та, примеси, и т.п.)
Поэтому такой кусок кабеля скорее всего не подойдет, нужен провод сечением 2,5 квадрата. Он даст падение 0,7 В на линии 10 м, что приемлемо.
А если другого провода нет? Есть два пути, чтобы снизить потерю напряжения в проводах.
1. Надо размещать источник питания 12,5 В как можно ближе к нагрузке. Если брать пример выше, 5 метров нас устроит. Так всегда и делают, чтобы сэкономить на проводе.
2. Повышать выходное напряжение источника питания. Это черевато тем, что с уменьшением тока нагрузки напряжение на нагрузке может подняться до недопустимых пределов.
Например, в частном секторе на выходе трансформатора (подстанции) устанавливают 250-260 Вольт, в домах около подстанции лампочки горят как свечи. В смысле, недолго. А жители на окраине района жалуются, что напряжение нестабильное, и опускается до 150-160 Вольт. Потеря 100 Вольт! Умножив на ток, можно вычислить мощность, которая отапливает улицу, и кто за это платит? Мы, графа в квитанции “потери”.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
Вывод по выбору сечения провода для постоянного напряжения:
Чем короче и толще провод, по которому течет постоянный ток, тем меньше падение напряжения на нём, тем лучше. То есть, потеря напряжения в проводах минимальна.
Если смотреть на таблицу 2, нужно выбирать значения сверху-справа, не переходя в “синюю” зону.
Для переменного тока ситуация та же, но вопрос не стоит столь остро – там мощность передается за счет повышения напряжения и понижения тока. См. формулу (1).
В заключение – таблица, в которой падение постоянного напряжения задано пределом 2% , а напряжение питания равно 12 В. Искомый параметр – максимальная длина провода.
Внимание! Имеется ввиду двухпроводная линия, например кабель, содержащий 2 провода. То есть, тот случай, когда через кабель длиной 1 м ток делает путь 2 м, туда-сюда. Я привёл этот вариант, т.к. он чаще всего встречается на практике. Для одного провода, чтобы узнать падение на нём напряжения, надо число внутри таблицы умножить на 2. Спасибо внимательным читателям!
Таблица 3. Максимальная длина провода для падения постоянного напряжения 2%.
| S,мм² I,A | 1 | 1,5 | 2,5 | 4 | 6 | 10 | 16 | 25 | 35 | 50 | 75 | 100 |
| 1 | 7 | 10,91 | 17,65 | 28,57 | 42,86 | 70,6 | 109,1 | 176,5 | 244,9 | – | – | – |
| 2 | 3,53 | 5,45 | 8,82 | 14,29 | 21,4 | 35,3 | 54,5 | 88,2 | 122,4 | 171,4 | – | – |
| 4 | 1,76 | 2,73 | 4,41 | 7,14 | 10,7 | 17,6 | 27,3 | 44,1 | 61,2 | 85,7 | 130,4 | – |
| 6 | 1,18 | 1,82 | 2,94 | 4,76 | 7,1 | 11,7 | 18,2 | 29,4 | 40,8 | 57,1 | 87 | 117,6 |
| 8 | 0,88 | 1,36 | 2,2 | 3,57 | 5,4 | 8,8 | 13,6 | 22 | 30,6 | 42,9 | 65,25 | 88,2 |
| 10 | 0,71 | 1 | 1,76 | 2,86 | 4,3 | 7,1 | 10,9 | 17,7 | 24,5 | 34,3 | 52,2 | 70,6 |
| 15 | – | 0,73 | 1,18 | 1,9 | 2,9 | 4,7 | 7,3 | 11,8 | 16,3 | 22,9 | 34,8 | 47,1 |
| 20 | – | – | 0,88 | 1,43 | 2,1 | 3,5 | 5,5 | 8,8 | 12,2 | 17,1 | 26,1 | 35,3 |
| 25 | – | – | – | 1,14 | 1,7 | 2,8 | 4,4 | 7,1 | 9,8 | 13,7 | 20,9 | 28,2 |
| 30 | – | – | – | – | 1,4 | 2,4 | 3,6 | 5,9 | 8,2 | 11,4 | 17,4 | 23,5 |
| 40 | – | – | – | – | – | 1,8 | 2,7 | 4,4 | 6,1 | 8,5 | 13 | 17,6 |
| 50 | – | – | – | – | – | – | 2,2 | 3,5 | 4,9 | 6,9 | 10,4 | 14,1 |
| 100 | – | – | – | – | – | – | – | 1,7 | 2,4 | 3,4 | 5,2 | 7,1 |
| 150 | – | – | – | – | – | – | – | – | – | 2,3 | 3,5 | 4,7 |
| 200 | – | – | – | – | – | – | – | – | – | – | 2,6 | 3,5 |
Наша полторашка по этой таблице может иметь длину только 1 метр. Падать на ней будет 2%, или 0,24В. Проверяем по формуле (4) – всё сходится.
Если напряжение выше (например, 24 В постоянного тока), то и длина может быть соответственно больше (в 2 раза).
Всё вышесказанное относится не только к постоянному, но и вообще к низкому напряжению. И при выборе площади сечения в таких случаях следует руководствоваться не только нагревом провода, но и падением напряжения на нём. Например, при питании галогенных ламп через понижающий трансформатор.
Прошу прокомментировать статью, у кого как теория совпадает с практикой?
Варианты определения ΔU
Метод векторов
В ходе проектирования электрической сети в основе лежит нагрузка, работоспособность которой необходимо обеспечить. Если кабель будет выбран неправильно, ΔU на нем не позволит правильно работать этой нагрузке. Асинхронные двигатели не достигнут заданных оборотов, трансформаторы на вторичных обмотках не обеспечат номинальные напряжения и т.д., и т.п. Для однофазной сети нагрузка разделяется на активную и реактивную составляющие.
Трехфазная сеть представляется как три самостоятельные однофазные сети. Они называются схемами замещения. Этот метод обеспечивает достаточно точные результаты, если нагрузка симметрична. Если симметрия нарушается, то анализ причин, которые этот процесс вызвали, также можно выполнить, используя этот метод. На основании известных величин можно построить векторную диаграмму и, меняя длину векторов соответственно поставленной задаче, определять те величины, которые необходимы.
Схема 1
Например, известны параметры, которые необходимы для нормальной работы нагрузки. Параметры линии также известны. Следовательно, задача сводится к определению векторного напряжения U1. Шаги, приводящие к появлению искомого вектора, показаны далее.
Схема 2
Длина вектора и его направление определяются исходя из закона Ома и направления вектора напряжения, определяющего ток (векторы тока и напряжения по направлению совпадают). Вектор напряжения, который получается как результат сложения активной и реактивной составляющих нагрузки (IR+IХ), – это и есть ΔU в линии, соединяющей источник напряжения U1 с нагрузкой. Из полученных векторов просто получить также и потери напряжения. Для этого векторы U1 и U2 совмещаются так, чтобы направление обоих было таким же, как у вектора U2. Разница между ними в длине – это будут потери напряжения.
Схема падения и потери напряжения Определение ΔU и потерь напряжения
Таблицы Кнорринга
Но заниматься построением векторов довольно-таки нудно. Тем более что за время существования потребности в проектировании электросетей для стандартных ситуаций придуманы решения более быстрые. К ним относятся таблицы Кнорринга. Стандартность ситуации для них состоит в постоянстве напряжения на входе кабеля или иного проводника (переменное напряжение с действующим значением 220 В)
Это важно как для одной фазы, так и для трех фаз. То есть в трехфазной электросети нагрузка должна быть симметричной
Также необходимо располагать величиной сечения токопроводящей жилы (в квадратных миллиметрах), длиной проводника (в метрах) и мощностью в нагрузке (в киловаттах). Получаем произведение мощности на длину, в столбце, начинающемся с подходящего сечения жилы, находим это значение, и в крайнем левом столбце смотрим ΔU на кабеле. Только и всего. Два варианта таблиц для напряжения однофазной и трехфазной электрической сети, а также одна для напряжения 12 В, показанные далее, читатель может использовать для расчетов.
Таблица 1 Таблица 2 Таблица 3
Для всех таблиц принято ограничение – жилы должны быть из меди. Если читателю встретится такое определение, как момент нагрузки, – это как раз и будет число из таблицы Кнорринга для провода, соответствующее произведению мощности на длину.
Точные расчеты по формулам
Если по тем или иным причинам метод векторов и таблицы не устраивают, можно использовать либо формулы, показанные далее, либо калькулятор онлайн, на них основанный. Таких калькуляторов в сети немало, и найти подходящий несложно.
Расчет по формулам ΔU по длине кабеля