Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи
, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
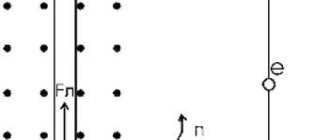
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против
движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой
; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят,
неэлектрическое
происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока
.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи
.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
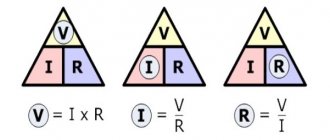
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой
(ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Что такое внутреннее сопротивление
В электрической цепи обязательно присутствует источник питания. Обычно, оценивая его параметры, указывают, какую разность потенциалов между клеммами он обеспечивает. Если говорить об идеальной модели источника питания, то можно предположить, что он способен обеспечить в электрической цепи любую мощность с учётом имеющейся разности потенциалов.
Реальные устройства в этом аспекте сильно отличаются друг от друга. Чтобы определить работоспособность аккумулятора важно знать, что такое внутреннее сопротивление. Обычно с течением времени и вследствие износа оно постепенно возрастает. Анализируя уровень и скорость того, как изменяется внутреннее сопротивление источника тока, можно принять решение о продолжении использования батареи или о необходимости её замены.
Сказанное следует пояснить на примере. Для запуска мотора автомобиля используется аккумулятор на 12 Вольт. Известно, что при этом сила тока может достигать 250 Ампер. Однако, если взять другой элемент питания с такой же разницей потенциалов, то вполне возможна ситуация, когда от него запуск мотора осуществить не получится.
В качестве примера такого источника можно рассмотреть несколько гальванических элементов, соединённых последовательно. Разница в двух рассматриваемых ситуациях определяется наличием различного внутреннего сопротивления.
Этот параметр для аккумулятора представляет собой сумму нескольких слагаемых: сопротивление каждого вывода, корпуса и используемого электролита. В некоторых источниках тока при этом могут учитываться дополнительные элементы, включённые в данную цепь.
Важно учитывать, что понятие омического сопротивления в этой ситуации неприменимо, поскольку требуется наличие в цепи только пассивных элементов. Когда создана замкнутая цепь, ток протекает не только по ней, но и внутри источника тока. Внутреннее сопротивление определяет величину потерь энергии в нём.
Его наличие в цепи можно проиллюстрировать ещё одним примером. Если на клеммах аккумулятора имеется 12 вольт, то на первый взгляд можно легко предсказать, какая сила тока будет при нагрузке 1 Ом. Очевидно, что нужно ожидать, что по цепи пройдёт ток, равный 12 Ампер.
На самом деле это утверждение не соответствует действительности: ток будет немного меньше — примерно 11.2 Ампера. Здесь нет никакого несоответствия физике. Ведь при расчёте дополнительно требуется учитывать сопротивление источника тока, из-за которого происходит расход энергии. Оно называется внутренним. Его можно мысленно представить как резистор, соединённый последовательно с источником тока.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением
этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором
, или
внешней нагрузкой
, или
полезной нагрузкой
). Всё это вместе называется
полной цепью
(рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи
.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание
. Через источник при этом потечёт максимальный ток —
ток короткого замыкания
:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника
.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока
. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь
. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС
.
От электростатики к электрокинетике
Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.
Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.
Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.
Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.
Вам это будет интересно Определение закона Ома, применяющегося для полной цепи
Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:
- 1800 г. — создание Вольтой гальванической батареи;
- 1826 г. — Ом формулирует свой закон для полной цепи;
- 1831 г. — обнаружение электромагнитной индукции Фарадеем.
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной
, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи
— это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Объясняем суть ЭДС «на пальцах»
Чтобы разобраться в том, что есть что, можно привести пример-аналогию. Представим, что у нас есть водонапорная башня, полностью заполненная водой. Сравним эту башню с батарейкой.
Вода оказывает максимальное давление на дно башни, когда башня заполнена полностью. Соответственно, чем меньше воды в башне, тем слабее давление и напор вытекающей из крана воды. Если открыть кран, вода будет постепенно вытекать сначала под сильным напором, а потом все медленнее, пока напор не ослабнет совсем. Здесь напряжение – это то давление, которое вода оказывает на дно. За уровень нулевого напряжения примем само дно башни.
То же самое и с батарейкой. Сначала мы включаем наш источник тока (батарейку) в цепь, замыкая ее. Пусть это будут часы или фонарик. Пока уровень напряжения достаточный и батарейка не разрядилась, фонарик светит ярко, затем постепенно гаснет, пока не потухнет совсем.
Но как сделать так, чтобы напор не иссякал? Иными словами, как поддерживать в башне постоянный уровень воды, а на полюсах источника тока – постоянную разность потенциалов. По примеру башни ЭДС представляется как бы насосом, который обеспечивает приток в башню новой воды.
Таблица удельных сопротивлений различных материалов
| Удельное сопротивление ρ, Ом*мм2/м | Удельное сопротивление ρ, Ом*мм2/м |
| Алюминий | 0,028 |
| Бронза | 0,095 – 0,1 |
| Висмут | 1,2 |
| Вольфрам | 0,05 |
| Железо | 0,1 |
| Золото | 0,023 |
| Иридий | 0,0474 |
| Константан ( сплав Ni-Cu + Mn) | 0,5 |
| Латунь | 0,025 – 0,108 |
| Магний | 0,045 |
| Манганин (сплав меди марганца и никеля – приборный) | 0,43 – 0,51 |
| Медь | 0,0175 |
| Молибден | 0,059 |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 |
| Натрий | 0,047 |
| Никелин ( сплав меди и никеля) | 0,42 |
| Никель | 0,087 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 – 1,4 |
| Олово | 0,12 |
| Платина | 0.107 |
| Ртуть | 0,94 |
| Свинец | 0,22 |
| Серебро | 0,015 |
| Сталь | 0,103 – 0,137 |
| Титан | 0,6 |
| Хромаль | 1,3 – 1,5 |
| Цинк | 0,054 |
| Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.