Симметричные
Симметричные цепи переменного тока предполагают соединение 3 фаз от источника (генератора) с тремя приемниками.
При этом создаются совершенно независимые трехфазные схемы. При этом используется соединение трех фаз генератора звездой. Для симметричных схем должны соблюдаться требования:
- Амплитуда должна быть для всех фаз одинаковой.
- ЭДС должна иметь угол сдвига 120 градусов.
- Угловые частоты должны быть равными.
Также учитывается принцип чередования ЭДС во времени. Если ротор генератора вращается по часовой стрелке (правое вращение), то происходит чередование прямого типа (A, B, C). Такая система считается симметричной.
Если ротор вращается против часовой стрелки (левое вращение), чередование считается обратным (A, C, B), но общая система ЭДС остается все так же симметричной.
Для симметричных схем применяется расчет по векторной гистограмме, приведенной ниже.
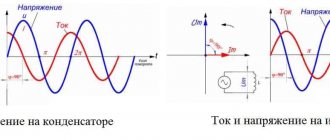
Закон Ома — основа электротехники
Это основное уравнение, используемое для изучения электрических цепей, было получено экспериментальным путем Георгом Симоном Омом. Он родился в Эрлангене Германии в 1787 году и поступил в университет этого города в 1805 году, где он получил докторскую степень. Георг преподавал математику в школах и проводил эксперименты по физике в школьной физической лаборатории, пытаясь понять принципы электромагнетизма.
В 1827 году он опубликовал статьи, в которых описана математическая модель того, как контуры проводят тепло в работах Фурье. Ом получил экспериментальные данные, на базе которых впервые смог сформулировать свой закон 8 января 1826 года. Он установил, что разность потенциалов между двумя точками в цепи равна произведению тока между ними на общее сопротивление всех электрических устройств. Чем больше напряжение батареи или ее общая разность электропотенциалов, тем больше будет ее ток. Аналогично, с большим сопротивлением он будет меньше.
Но его исследования не нашли должного понимания и Георг оставил свою работу в Кельне. Только в 1833 году он получил должность профессора в Нюрнберге. Выводы Ома послужили катализатором для новейших исследований по электричеству. В 1841 году ученого наградили медалью Копли, а в 1872 году «Ом» был принят в качестве единицы сопротивления в электрических цепях.
Закон Ома для полной электрической цепи описывает протекание тока через проводящие металлы, когда применяются различные уровни напряжения. Некоторые материалы, такие как электропровода, имеют небольшое сопротивление току — этот тип материала называется проводником.
Важно! В других случаях материал может препятствовать протеканию тока, но, тем не менее, допускает его использование. В электрических цепях эти компоненты часто называют резисторами. Существуют материалы, которые практически не пропускают ток, они называются изоляторами.
Несимметричные
Несимметричные цепи предполагают разницу сопротивлений на каждой фазе. Подобная разница может возникнуть при возникновении обрыва одного проводника или нейтрали, его плохого контакта, короткого замыкания. Например, при обрыве нейтрального провода возникает:
- Увеличение сопротивления нейтрали.
- Полное отсутствие проводимости.
- Увеличение напряжения.
- Максимальное искажение фазных напряжений.
При расчете несимметричной цепи также берется расчет соединения источника с приемниками по схеме звезда. Разница состоит в дополнительном расчете смещений, сдвигов фаз и величин сопротивления каждого проводника.
Ниже приведена векторная диаграмма несимметричной цепи.
Измерение мощности
Измерение активной мощности в сетях производится с помощью ваттметра
Цифровой ваттметр Аналоговый ваттметр
В зависимости от схемы соединения нагрузки и его характера (симметричная или несимметричная) схемы подключения приборов могут разниться. Рассмотрим случай с симметричной нагрузкой:
Схема включения ваттметра при симметричной нагрузке
Здесь измерение проводится всего лишь в одной фазе и далее согласно формуле умножается на три. Этот способ позволяет сэкономить на приборах и уменьшить габариты измерительной установки. Применяется, когда не нужна большая точность измерения в каждой фазе.
Измерение при несимметричной нагрузке:
Схема включения ваттметра при несимметричной нагрузке
Этот способ более точный, так как позволяет измерить мощность каждой фазы, но это требует трех приборов, больших габаритных размеров установки и обработки показаний с трех приборов.
Измерении в цепи без нулевого проводника:
Схема включения ваттметра при отсутствии нулевого провода
Эта схема требует двух приборов. Этот способ основывается на первом законе Кирхгофа
IA+IB+IC=0. Из этого следует, что сумма показаний двух ваттметров равна трехфазной мощности этой цепи. Ниже показана векторная диаграмма для данного случая:
Векторная диаграмма включения двух ваттметров при различных видах нагрузки
Мы можем сделать вывод, что показания приборов зависят не только от величины, но еще и от характера нагрузки.
Из диаграммы следует, что мы можем определить показание приборов аналитически:
Проанализировав полученный результат можем сделать вывод что, при преобладании активной нагрузки (φ=0) результаты измерения ваттметров тождественны (W1=W2). При активной и индуктивной (R-L) показания W1 меньше чем W2 (W12), при φ>600 показания W1 вообще отрицательные (W1<0).
При активной и емкостной(R-C) и W1>W2, а при φ<-600 показания W2 <0.
При современном развитии техники появились цифровые ваттметры. Они в отличии от аналоговых меньше в размерах, гораздо легче и менее габаритны. Более того цифровые ваттметры могут фиксировать ток, напряжение, измерять cosφ в сети и другое. Они позволяют в режиме реального времени отслеживать различные величины и выдавать предупреждения при их отклонении. Это очень удобно и не требуется проводить измерения тока, напряжения, а потом математически это все высчитывать. Цифровой ваттметр заключен в корпус и подключается (для бытовых потребителей) самым обычным способом – как и обычный потребитель — втыканием вилки в розетку.
Построение диаграммы
Векторная диаграмма предполагает в своей основе следующие значения:
- Точку начала отсчета N для всех трех отдельных фаз.
- Векторное направление ABC как отдельных проводников источника напряжения (генератора). Каждый вектор имеет заданную длину, равную своему напряжению.
- Окончание векторов AВ, BС, CА, как приемников напряжения.
Данные значения дополняются единицей времени, за которое ток, под определенным напряжением и силой достигает приемников. Исходя из построения получаем результат: UAB=UBC=UCA.
А это значит то, что если фазная система напряжений симметрична, то линейная система также симметрична и равна, а кроме того имеет сдвиг на 120 градусов. Это простое определение вектора трехфазной цепи.
Переменный ток представляет собой синусоиду, которая может быть графически наложена на ось координат. При этом вектор имеет угловую скорость вращения, которая равна угловым частотам тока. При построении необходимо также учесть то, что вектор является графическим изображением амплитуды колебания, в котором угол колебания равен начальной точке отсчета.
Например, за ось координаты выбрано значение 0. Также известно значение угла смещения. Далее стоит провести вектор «Im», который определяет направление движения тока. При построении вектора с использованием этих значений станут видны параметры опережения, отставания или сдвига фазы. Таким образом можно визуально увидеть разницу величин на каждом проводнике схемы.
Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой,
т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
- фаза как аргумент синусоидально изменяющейся величины;
- фаза как составная часть многофазной электрической системы.
Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений.
Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.
Источником трехфазного напряжения является трехфазный генератор, на статоре которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно друга на эл. рад. На рис. 1 каждая фаза статора условно показана в виде одного витка. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 1 ротор условно изображен в виде постоянного магнита, что используется на практике при относительно небольших мощностях). При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на рад. (см. рис. 2).
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
— экономичность передачи электроэнергии на большие расстояния;
— самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором;
— возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств;
— уравновешенность симметричных трехфазных систем.
Для рассмотрения важнейшего свойства уравновешенности
трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы.
Система ЭДС (напряжений, токов и т.д.) называется симметричной,
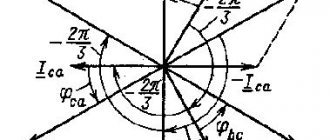
если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол . В частности векторная диаграмма для симметричной системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена на рис. 3.
| Рис.3 | Рис.4 |
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4).
Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными.
Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б).
Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям.
Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной.
Схемы соединения трехфазных систем
Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 120°. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система.
В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике.
Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду
и
в треугольник.
В свою очередь при соединении в звезду система может быть
трех-
и
четырехпроводной.
Соединение в звезду
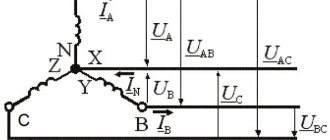
На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода.
Линейным
называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется
нейтральной
(на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки).
Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным
(на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется
трехпроводной,
с нейтральным проводом –
четырехпроводной.
Все величины, относящиеся к фазам, носят название фазных переменных,
к линии —
линейных.
Как видно из схемы на рис. 6, при соединении в звезду линейные токи и равны соответствующим фазным токам. При наличии нейтрального провода ток в нейтральном проводе . Если система фазных токов симметрична, то . Следовательно, если бы симметрия токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке при несимметрии самой нагрузки.
Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной точке N; — фазные напряжения нагрузки.
Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
| ; | (1) |
| ; | (2) |
| . | (3) |
Отметим, что всегда — как сумма напряжений по замкнутому контуру.
На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае
| (4) |
Обычно при расчетах принимается . Тогда для случая прямого чередования фаз
, (при
обратном чередовании фаз
фазовые сдвиги у и меняются местами). С учетом этого на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений. Однако при симметрии напряжений эти величины легко определяются непосредственно из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат по вектору (его начальная фаза равна нулю), отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их модули определяем в соответствии с (4). Так для линейных напряжений и получаем: ; .
Соединение в треугольник
В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).
Для симметричной системы ЭДС имеем
.
Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8 токи будут равны нулю. Однако, если поменять местами начало и конец любой из фаз, то и в треугольнике будет протекать ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать порядок соединения фаз: начало одной фазы соединяется с концом другой.
Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9.
Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
Аналогично можно выразить линейные токи через фазные токи генератора.
На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
| . | (5) |
В заключение отметим, что помимо рассмотренных соединений «звезда — звезда» и «треугольник — треугольник» на практике также применяются схемы «звезда — треугольник» и «треугольник — звезда».
Литература
- Основы
теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А.
Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой принцип действия у трехфазного генератора?
- В чем заключаются основные преимущества трехфазных систем?
- Какие системы обладают свойством уравновешенности, в чем оно выражается?
- Какие существуют схемы соединения в трехфазных цепях?
- Какие соотношения между фазными и линейными величинами имеют место при соединении в звезду и в треугольник?
- Что будет, если поменять местами начало и конец одной из фаз генератора при соединении в треугольник, и почему?
- Определите комплексы линейных напряжений, если при соединении фаз генератора в звезду начало и конец обмотки фазы С поменяли местами.
- На диаграмме на рис. 10 (трехфазная система токов симметрична) . Определить комплексы остальных фазных и линейных токов.
- Какие схемы соединения обеспечивают автономность работы фаз нагрузки?