сглаживающие и ЭМП-фильтры для импульсных преобразователей

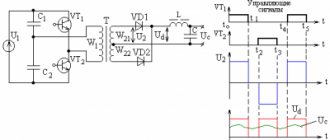
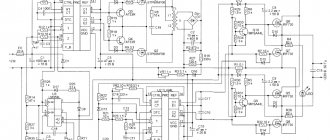
Входные ЭМП-фильтры

Входные и выходные фильтры — необходимая составляющая практически любой электронной системы, в состав которой входят импульсные преобразователи или быстродействующие компоненты. И хотя входные ЭМП-фильтры и выходные сглаживающие фильтры служат разным целям, их конфигурация в ряде случаев может быть схожа.
Основное назначение входных фильтров заключается в защите от электромагнитных помех (ЭМП), генерируемых преобразователем, а также защита от возможных помех со стороны сети. Во многих случаях наилучшим выбором является покупной ЭМП-фильтр, в котором предусмотрена фильтрация дифференциальных и синфазных помех. Эти фильтры устанавливаются между питающей сетью и AC/DC-преобразователем. В состав фильтров входят магнитосвязанные дроссели и емкости. В общем случае схема такого фильтра представлена на рис. 1.

Рис. 1. Схема синфазного и дифференциального ЭМП-фильтра

В этом ЭМП-фильтре последовательно включены два фильтра. Ближний к сети ЭМП-фильтр дифференциальных помех состоит из конденсаторов CY5, CY6, CX2 и магнитосвязанного двухобмоточного дросселя LDM. Последовательно с ним установлен ЭМП-фильтр дифференциальных помех, в состав которого входят конденсаторы CY3, CY4, CX1 и магнитосвязанный двухобмоточный дроссель LCM.

Как видно из рисунка, ЭМП-фильтры синфазных и дифференциальных помех имеют схожую конфигурацию за исключением расположения начала и конца обмоток дросселей LDM и LCM. Различие объясняется следующим образом. Токи дифференциальных помех в фазе и нейтрали протекают в разных направлениях, а токи синфазных помех в фазе и нейтрали текут в одном направлении и замыкаются через корпус или заземление. Таким образом, в обоих дросселях магнитные потоки, создаваемые двумя обмотками, складываются. Следовательно, индуктивность дросселя возрастает, и ЭМП-фильтр работает как классический LC-фильтр.

Описанные выше ЭМП-фильтры, как правило, устанавливаются в линиях сетевого напряжения 220 В на входе AC/DC-преобразователя. ЭМПфильтры производятся многими известными на российском рынке электроники компаниями, среди которых Murata, Epcos, Würth Elektronik и многие другие.

Автор настоятельно рекомендует использовать покупные фильтры и не пытаться изготавливать их самостоятельно из дискретных компонентов. Не следует использовать ЭМП-фильтры для цепей переменного тока в цепях постоянного тока. Постоянный ток создаст подмагничивание дросселей фильтра, а всплески токов помех приводят к насыщению сердечника дросселя, что влечет за собой уменьшение их индуктивности и, следовательно, фильтрующих свойств.

Однако не всегда можно использовать готовые ЭМП-фильтры. Например, в распределенных системах питания в цепях постоянного тока после шинного преобразователя или перед ним может понадобиться установить ЭМП-фильтр перед PoL-преобразователем. В этом случае, скорее всего, придется создать такой фильтр на дискретных компонентах, особенно если невелика мощность преобразователя, перед которым устанавливается фильтр.

Примером может служить LC-фильтр, показанный на рис. 2. Поскольку фильтр описывается уравнением 2‑го порядка и представляет собой хорошо известное колебательное звено, мы лишь приведем окончательные соотношения.

Рис. 2. ЭМП-фильтр LC-типа

Собственная частота колебательного звена определяется из соотношения (1):

ω0 = 1/√LC. (1)

Величина демпфирования определяется из соотношения (2):

β = (R/2) × (√C/L). (2)

В схеме на рис. 2 отсутствует резистор R в явном виде, поэтому такой фильтр называется недемпфированным, но это не значит, что R = 0 и любое входное воздействие порождает в фильтре незатухающие колебания. Величина R складывается из омического сопротивления дросселя RDC, эквивалентного последовательного сопротивления конденсатора (ESR) и сопротивления проводников. Передаточная характеристика этого фильтра показана на рис. 3.

Рис. 3. Передаточная характеристика LC-фильтра

Как видно из этого рисунка, чем меньше степень демпфирования β, тем ярче выражен резонансный пик в частотной области. Также при условии β<1, чем меньше β, тем более явно выражен колебательный переходный процесс во временной области. В последнем случае вполне уместен афоризм «лучшее – враг хорошего». Известны случаи, когда из-за использования в шинах постоянного тока высококачественных конденсаторов с очень малым ESR возникали колебания напряжения на шине именно из-за малой величины ESR, т. к. при сокращении ESR уменьшалась степень демпфирования и возрастала колебательность переходного процесса.

Следует учесть еще одно обстоятельство: ЭМП-фильтр будет работать так, как рассчитано, лишь в том случае, если его выходной импеданс существенно меньше, чем входной импеданс преобразователя. В противном случае подключение к выходу фильтра преобразователя заметно исказит характеристики фильтра. И фильтр может исказить работу преобразователя.

Входную цепь преобразователя в общем случае можно представить в виде последовательной RLC-цепочки. Таким образом, у частотной характеристики импеданса появится экстремум в виде минимума. Чтобы устранить взаимовлияние ЭМП-фильтра и преобразователя, желательно, чтобы выходной импеданс преобразователя был на порядок меньше входного импеданса ЭМП-фильтра.

На рис. 4 приведен пример частотной зависимости импедансов ЭМП-фильтра и преобразователя. Из этого рисунка, а также из приведенных выше соображений ясно, что величина демпфирования не должна быть слишком малой. С другой стороны, чрезмерное увеличение β устранит колебательность, переходный процесс станет апериодическим и затянется во времени. Как правило, оптимальное значение β следует выбирать в пределах 0,5–1,0.

Рис. 4. Частотные зависимости импедансов ЭМП-фильтра и преобразователя

При недемпфированном фильтре (рис. 2) значение R в соотношении (2) в основном определяется суммой RDC + ESR, но этой величины недостаточно, чтобы увеличить β до 0,7–1,0. Следовательно, требуется ввести дополнительное сопротивление. Наилучший вариант введения демпфирующей цепочки показан на рис. 5. Цепочка Z3 состоит из последовательно соединенных резистора Rd и конденсатора Cd. Последний блокирует постоянное напряжение и предотвращает дополнительную потерю мощности на резисторе Rd. Коэффициент демпфирования ЭМП-фильтра с демпфирующей цепочкой описывается выражением (3):

βd = (n/n + 1) [(Rd/2) × (√C/L)], (3)

где n = Cd/C.

Рис. 5. Демпфированный LC-фильтр

Из практических соображений величина n должна находиться в пределах 4–7 единиц. На рис. 6 показана частотная зависимость импедансов демпфированного и недемпфированного фильтров. Резонансный пик демпфированного ЭМП-фильтра существенно меньше, чем у недемпфированного. Демпфирующую цепочку можно составить из последовательной RL-цепочки и подсоединить ее параллельно индуктивности фильтра, но это не самое лучшее, на наш взгляд, решение, т. к. увеличивается мощность рассеяния на резисторе.

Рис. 6. Частотные зависимости импедансов демпфированного и недемпфированного LC-фильтра

Если последовательно включить несколько LC-фильтров, увеличится крутизна спада АЧХ ЭМП-фильтра в области ω>ω0, и улучшится фильтрация помех, но, как представляется автору, такое решение не имеет смысла. Габариты решения заметно возрастут, а увеличение крутизны спада АЧХ фильтра не принесет практической выгоды. Рабочая частота PoL-преобразователей в настоящее время находится в диапазоне примерно 1–2 МГц.

С учетом требований стандартов частота среза ЭМП-фильтра должна находиться в пределах нескольких кГц. Если выбрать величину β ≈ 1, то ослабление на частоте 1 МГц составит 50–60 дБ, что вполне достаточно для подавления помех. Если все же потребуется более значительное ослабление, возможно, следует подумать не о применении двухкаскадного ЭМП-фильтра, а проанализировать систему питания и принять иные меры к уменьшению помех.

Улучшаем компьютерный блока питания

Наши друзья меньшие (Китайцы) заполонили рынок электроники, но не всегда они бывают добросовестные, но многие дорогие модели компьютерных блоков питания достойные в своем классе. Но все-же большинство блоков питания, как я их называю кастрированные, то есть когда печатная плата была разработана под одни элементы, а в ней впаяны другие, и не все, особенно это по по входным фильтрам, их почти никогда нет в дешевых моделях.

Структурная схема ATX

Главный недостаток всех дешевых БП

осциллограмма напряжений +5В дешевого БП.

Выходные сглаживающие фильтры

В качестве сглаживающих выходных фильтров используются те же LC-фильтры, которые были рассмотрены выше. Однако в данном случае такие фильтры не удастся заменить покупными, и их всякий раз приходится рассчитывать разработчику. Выходной сглаживающий фильтр позволяет снизить пульсации выходного напряжения до единиц мВ или даже нескольких сотен мкВ. Уменьшение амплитуды пульсаций до десятков мкВ едва ли возможно, даже если увеличить число каскадов выходного фильтра.

Уменьшению пульсаций помешают паразитные составляющие компонентов фильтра и проводников печатной платы. Кроме того, из-за джиттера частоты коммутации в спектре выходного напряжения могут возникать низкочастотные составляющие вплоть до нескольких Гц. Их, конечно, невозможно подавить сглаживающим фильтром. Таким образом, если требуется ограничить пульсации выходного напряжения вплоть до мкВ, после сглаживающего фильтра в цепь питания устанавливается LDO-регулятор.

Рис. 7. Сглаживающий фильтр на выходе повышающего преобразователя

Рассмотрим наиболее распространенную конфигурацию сглаживающего фильтра – π-фильтр (или П-фильтр). Схема его включения в цепь повышающего преобразователя приведена на рис. 7 [1]. Резонансная частота этого фильтра определяется из выражения (4).

В отличие от ЭМП-фильтра, сглаживающий фильтр входит в состав контура обратной связи, поэтому частота среза фильтра не должна быть меньше 10–20% частоты коммутации. В противном случае уменьшается устойчивость системы из-за запаздывания в петле обратной связи, что приводит к затягиванию переходных процессов, а также к ухудшению устойчивости из-за уменьшения запаса по фазе. Как и в случае с ЭМП-фильтрами, в сглаживающий фильтр необходимо ввести демпфирующую цепочку. На рис. 7 показаны три возможных варианта цепочек демпфирования.

Вариант демпфирования 1 с введением резистора RFILT представляется самым простым и экономичным, но введение этого резистора ослабляет эффективность фильтра. Кроме того, уменьшается импеданс параллельной RL-цепочки фильтра. Вариант демпфирования 2 наиболее эффективен, т. к. эта цепочка улучшает характеристику фильтра, но увеличивает стоимость из-за использования керамического конденсатора. На первый взгляд может показаться, что вариант демпфирования 3 – самый эффективный. Однако в этом случае требуется наибольшая емкость конденсатора. Следовательно, возрастает стоимость решения. К тому же, поскольку введение этой цепочки уменьшит полосу пропускания петли обратной связи, этот вариант следует исключить из рассмотрения.

Для высокочастотных преобразователей с малым выходным током имеется еще один нетривиальный вариант сглаживающего фильтра — вместо дросселя в фильтре используется резистор. Рассмотрим простой пример, где в качестве выходного фильтра PoL-преобразователя с частотой коммутации 2 МГц и выходным током 20 мА применяется RC-фильтр. Пусть сопротивление резистора равно 10 Ом, а емкость конденсатора — 1 мкФ. Частота среза этого фильтра составит около 16 кГц; учитывая ослабление 20 дБ/декаду, получим, что пульсации с частотой 2 МГц ослабляются более чем в 100 раз. Однако придется смириться с падением напряжения 200 мВ на резисторе.

Заметим, что расчет фильтров носит приблизительный характер и расчетные параметры обязательно должны проверяться путем макетирования фильтра совместно с преобразователем. На величину емкости фильтра влияет напряжение заряда, частота пульсации тока, температура емкости. Индуктивность дросселя фильтра нелинейно зависит от тока. Кроме того, на характеристики фильтра будет влиять и преобразователь. Эти изменения невозможно учесть в практических расчетах. Помощь при разработке фильтра оказывают фирменные САПР для расчета фильтров. Например, схему расчета сглаживающего фильтра можно найти в [1]. Для расчета ЭМП-фильтра можно воспользоваться средствами [2].

Принятые обозначения

При аналитическом анализе процессов используются величины:

Uн

,
Iн
— эффективные значения напряжения и тока нагрузки;

Udмин

,
Udном
,
Udмакс
— минимальное, номинальное и максимальное напряжения источника питания;

Zн

, φ — сопротивление и угол активно-индуктивной нагрузки;

= 1/
T
,
fн
= 1/
h
— выходная и несущая частоты (
T
,
h
— их периоды);

Ω = f

/
fн
— относительная выходная частота;

x̄L

= 2π
fL
/
ZН
,
ȳC
= 2π
fCZН
— относительные сопротивление дросселя и проводимость конденсатора фильтра на основной частоте;

α, β, χ = α + β — углы между основными гармониками напряжений и токов фильтра (согласно векторной диаграмме рис. 2б);

— коэффициент трансформации;

— максимальная глубина модуляции ШИМ-импульсов;

(
t
),
f̂
(
t
),
f̃
(
t
) — функция, ее основная и пульсационная составляющие;

(
t
) — переключающая функция.

Рис. 2. а) Эквивалентная схема LC-фильтраж б) векторные диаграммы

Относительные значения токов и напряжений обозначаются черточкой сверху, амплитудные — индексом «m

», максимальные — индексом «макс», a пульсации — индексом «П». В качестве базовых величин для относительных напряжений и токов выбраны эффективные значения напряжения и тока нагрузки. При анализе частично учитываются прямые падения напряжений на вентилях схемы инвертора (транзистора — Δ
UVT
, диода — Δ
UVD
). Остальные элементы схем предполагаются идеальными.

Подход «локального усреднения»

Применяемый подход к анализу процессов в ШИМ-инверторах основан на двух широко распространенных методах расчета. Его можно трактовать как конкретизацию метода основной гармоники для данного типа преобразователей [7] и как некую «модернизацию» метода переключающих функций [11].

Временные функции в данном случае искажены пульсацией, но имеют либо явно выраженную синусоидальную основу выходной частоты (токи фильтра), либо почти синусоидальные (выходное напряжение). Анализ фильтра выполняется по следующей общей схеме: определяются напряжения и токи элементов основной частоты; интегрально рассчитываются пульсации токов, а по ним — пульсация и коэффициент несинусоидальности выходного напряжения; «наложением» отдельных составляющих определяются полные токи и напряжения компонентов, а по ним — токи дросселя, конденсатора и проч.

На рис. 2а приведена схема фильтра, возбуждаемого эквивалентным источником ШИМ-напряжения v

(
t
), причем в токах и напряжениях элементов доминируют гармоники основной (выходной) частоты. Это позволяет представить временные функции
fi
(
t
) в виде суммы основной и пульсационной составляющих:

Сущность подхода «локального усреднения» заключается в следующем. Если в пределах периода несущей частоты напряжение нагрузки считать постоянным, то можно определить параметры пульсации токов фильтра, имеющей треугольную форму. Эти параметры зависят от коэффициента заполнения ШИМ-импульсов и меняются от такта к такту. При сравнительно больших отношениях несущей и выходной частот, что обычно имеет место на практике, среднее значение ШИМ-импульса упрощенно представляется синусоидальной функцией выходной частоты и амплитудой, пропорциональной глубине модуляции М

. Тем самым пульсации тока дросселя (конденсатора) фильтра «приписывается» модуляционная огибающая, и удается записать конечное и достаточно точное выражение в виде функции от
М
. В итоге получаются замкнутые аналитические выражения для результирующих токов элементов фильтра. Далее расчет ведется оперированием ими.

Сетевой выпрямитель напряжения: самая популярная конструкция

Правило №3: после выхода с фильтра напряжение подается на схему выпрямителя, состоящего в базовой версии из диодного моста и электролитического конденсатора.

В ходе электрического преобразования форма синусоиды, состоящая из полуволн противоположных знаков, вначале меняется на сигнал положительного направления после диодной сборки, а затем эти пульсации сглаживаются до практически постоянной амплитудной величины 311 вольт.

Такой сетевой выпрямитель напряжения заложен в работу всех блоков питания.

Расчет результирующих величин при ШИМ-2

Для эффективного значения полного тока дросселя легко получить

Пульсация тока дросселя полностью протекает через конденсатор, поэтому

Для эффективного значения полного тока конденсатора получается

Как следует из рис. 5, пульсация напряжения конденсатора изменяется параболически, причем амплитуды обеих парабол в k

-м такте определяются следующим образом:

где UСПm

— максимальная амплитуда пульсации, имеющая место при γ
k
= 0,5.

Рис. 5. Диаграммы пульсаций тока и напряжения конденсатора фильтра

Если определять эффективное значение параболической функции (19) за k

-й такт и геометрически вычитать из последнего псевдопостоянную составляющую (определяется интегрированием пульсации), то для эффективного значения всей пульсации получим:

В относительных единицах это и есть коэффициент несинусоидальности ξ:

Теоретически М

изменяется в пределах 1≥
M
≥0, и, как следует из (20), ξ меняется в диапазоне ξ = (0,4346–0,7303)
UСПm
. Практически
М
= 0,85–0,95 и ξ = (0,4499–0,4866)
ŪСПm
. Если рассчитать ξ по максимальной пульсации, как обычно поступают на практике, то мы получили бы 0,7071
ŪСПm
, т. е. ошибка составляла бы 31,2–36,4%, что существенно. Учитывая важность ξ для расчета параметров фильтра, формулу (20) можно считать хорошим подспорьем в пользу применяемого здесь подхода к анализу.

Коэффициент трансформации n

и максимальная глубина модуляции
М
зависят от схемы коммутатора инвертора. В частности, для мостовой схемы коммутатора имеем:

где t̄kмакс

=
tkмакс
/
h
— максимальное относительное время коммутации.

Расчет основных гармоник

При расчете основных гармоник напряжение и ток нагрузки предполагаются синусоидальными. Из векторных диаграмм (рис. 2б) можно найти напряжения и токи элементов фильтра в относительных единицах:

Временные функции основных гармоник выражаются в виде:

где V1m

— амплитуда основной гармоники ШИМ-импульсов на входе фильтра, а амплитуды
UНm
,
UL1m
,
IL1m
и
IC1m
определяются умножением соответствующих эффективных значений на коэффициент √2.

Измерение излучаемых помех

Метод измерения излучаемых помех частотой выше 30 МГц описан в базовом стандарте IEC CISPR16–2-3. Для измерений такого рода, как правило, используется безэховая комната с проводящим полом или безэховая камера. И в этом случае испытуемое устройство помещается на непроводящий стол (для переносных или настольных устройств) или на пол. Чтобы иметь возможность во время измерений поворачивать испытуемое устройство вокруг его собственной оси в исходном состоянии, оно помещается на поворотный стол (рис. 10). В сравнительно больших безэховых помещениях приемная антенна устанавливается на расстоянии 10 м от испытуемого устройства на высоте, которая соответствует максимальной величине электрического поля на каждой частоте измерения. Кроме того, ориентация этой антенны меняется, что обеспечивает горизонтальную и вертикальную поляризацию. В небольших безэховых камерах расстояние между антенной и испытуемым устройством составляет 3 м. Высота антенны должна быть фиксированной, а пол между испытуемым устройством и антенной покрыт поглощающим материалом.

Рис. 10. Установка для измерения излучаемых помех в безэховых комнатах или камерах

Переходная характеристика

Выходное напряжение должно оставаться стабильным при изменениях напряжения на входе импульсного преобразователя. Аналогично, в случае внезапного снижения или повышения выходного тока выходное напряжение должно быть быстро отрегулировано. На рисунке 10 показана переходная характеристика импульсного контроллера с регулируемой устойчивостью (кривая желтого цвета) с выходным напряжением 5 В при внезапном изменении нагрузочного тока с 0 до 1 А (зеленая кривая).
Рис. 10. Переходная характеристика устойчивого импульсного контроллера

При внезапном изменении нагрузочного тока управляющая схема должна быстро скорректировать выходное напряжение до заданного уровня. Выходное напряжение не должно значительно меняться в результате отклика на скачок – иначе из-за перенапряжения могут повредиться электронные цепи. В идеальном случае после скачка нагрузки выходное напряжение быстро корректируется до установленной величины; при этом отсутствуют выбросы и даже звон. Звон на этапе компенсации обусловлен нестабильной работой импульсного преобразователя. Функционирование контроллера импульсного ИП считается устойчивым, если он достаточно быстро реагирует на скачкообразное изменение нагрузки и своевременно компенсирует это изменение.

Измерения согласно стандарту IEC CISPR 22

Рассмотренные выше измерения были выполнены согласно стандарту IEC CISPR16–2-1. Благодаря схеме стабилизации импеданса линии асимметричное напряжение было изолировано и приравнено к синфазному напряжению, которое затем сравнивалось с предельным значением из стандарта IEC CISPR 22 на устройства для индивидуального и коммерческого применения (Class B). В отношении компонентов источника питания (в т. ч. к импульсным контроллерам всех типов) непосредственно действующие стандарты по ЭМС отсутствуют.

Необходимо установить категорию всей системы, в которой применяется импульсный преобразователь, и испытать ее в соответствии со стандартами, которые действуют в отношении изделия или семейства изделий. В рассмотренном примере за основу был взят стандарт IEC CISPR 22 для ИТ-приложений. Предельные значения из CISPR 22 также указаны в общем стандарте IEC 61000–6–3. В случаях отсутствия стандартов для конкретных устройств применяются общие стандарты.

Выводы

Рассмотрение параметров выходного сглаживающего LC-фильтра в совокупности с другими основными характеристиками инвертора и с учетом специфических особенностей ШИМ позволяет оптимизировать выбор фильтра.
Применение аппарата «локального усреднения» в сочетании с методами основной гармоники и переключающих функций позволяет исчерпывающе анализировать процессы в выходном фильтре ШИМ-инверторов, получать компактные и в то же время достаточно точные аналитические выражения для расчета и выбора параметров.
Расчет параметров можно непосредственно выполнять посредством приведенных здесь аналитических соотношений, точность которых у большинства величин не ниже 1%, а в ряде случаев — не ниже 2–3%. В более ответственных случаях можно воспользоваться приведенными результатами.
При прочих равных условиях коэффициент несинусоидальности выходного напряжения инвертора в приемлемом на практике диапазоне глубины модуляции (M
= 0,85–0,95) при ШИМ-2 примерно в 1,8 раза больше, чем при ШИМ-3.

Литература

Барегамян Г. В. Исследование транзисторного преобразователя с синусоидальным выходным напряжением // Тезисы доклада на Всесоюзной научно-технич. конф. «Применение в технологических процессах машиностроительного производства полупроводн. преобразоват. частоты». Уфа. 1980.
Барегамян Г. В. Выбор параметров LC-фильтра транзисторного инвертора с ШИМ и синусоидальным выходным напряжением // Тезисы доклада на Межведомственном научно-технич. совещании «Проблемы электромагнитной совместимости силовых полупроводниковых преобразователей». Таллин. 1982.
Барегамян Г. В., Маргарян В. В., Симонян Г. Р. Расчет выходного LC-фильтра инвертора с ШИМ // Деп. в АрмНИИНТИ 08.06.98. № 85-Ар98. Ереван. 1998.
Барегамян Г. В. Автоматизация расчета инвертора с трехуровневой ШИМ // Моделирование, оптимизация, управление: Сборник научных трудов / ГИУА. Ереван. 2001. Вып. 4.
Барегамян Г. В. Автоматизация расчета инверторов с синусоидальным выходным напряжением и двухуровневой широтно-импульсной модуляцией // Изв. НАН РА и ГИУА. Серия ТН. 2001. Т. 55. № 3.
Барегамян Г. В. Основы синтеза стабилизированных транзисторных преобразователей с широтно-импульсной модуляцией: Дис. на соискание д-ра техн. наук. Ереван, 2006.
Ковалев Ф. И., Мустафа Г. М. Использование метода первой гармоники при проектировании стабилизированных инверторов // Электротехника. 1982. № 3.
Моин В. С. Стабилизированные транзисторные преобразователи. М.: Энергоатомиздат. 1986.
Мосткова Г. П., Толкачев А. И. Расчет выходных фильтров автономных инверторов // Электротехн. промышленность. Сер. Преобр. техника. 1971. № 22.
Мустафа Г. М. Расчет импульсно-модулированных инверторов с синусоидальным выходным напряжением // Электротехника. 1988. № 2.
Руденко В. С., Сенько В. И., Чиженко И. М. Основы преобразовательной техники. М.: Высшая школа. 1980.
Адамия Г. Г., Беркович Е. И., Картавых А. С. и др. Статические агрегаты бесперебойного питания. М.: Энергоатомиздат. 1992.

Ос лабление пульсаций

На практике для ослабления остаточных пульсаций до уровня в несколько мВ и подавления высокочастотных компонентов применяется, как правило, LC-фильтр нижних частот. На рисунке 5 показана схема такого фильтра, который можно реализовать с помощью неэкранированного дросселя WE-PD2 и стандартного электролитического конденсатора.
Рис. 5. Простая схема фильтра нижних частот

Рис. 6. Двухкаскадный выходной фильтр

Если помехи должны полностью отсутствовать на выходе, наряду с LC-фильтром нижних частот применяется ФНЧ во втором каскаде (см. рис. 6). Недорогой двухкаскадный фильтр можно реализовать с помощью дросселя WE-PD2 и SMD-феррита серии WE-MPSB.

Компоненты LFILTER и CFILTER1 работают как ФНЧ , который фильтрует сигнал тактовой частоты контроллера импульсного ИП и подавляет гармонические колебания. Далее ВЧ -составляющие выходного напряжения контроллера преобразуются в тепло с помощью ферритовой бусины SMD, а CFILTER2 ослабляет их амплитуду. Выходной фильтр этого типа уменьшает величину остаточной пульсации до нескольких мВ и обеспечивает питание даже чувствительных аналоговых цепей.

Расчет пульсационных составляющих при ШИМ-3

При трехуровневой ШИМ (ШИМ-3) на входе фильтра формируется напряжение с уровнями ±Vm

, 0. Выполнив аналогичные шаги для вывода формул (4)–(12), получим следующие выражения:

В данном случае коэффициент γ есть модуль переключающей функции F

(ϑ), т. е.

Тогда с учетом (22) для основной составляющей пульсации тока дросселя имеем

Для эффективного значения этой пульсации можно получить

Получается, что при тех же М

= 0,85–0,95 имеем
ĪLП
≈ (0,3928–0,4365)
ĪLПm
, т. е. при одинаковых амплитудах пульсации тока ее эффективное значение при ШИМ-3 примерно на 3–5% больше, чем при ШИМ-2.