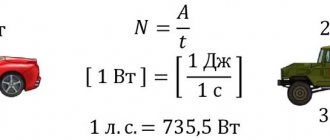Формула механической мощности — средняя и мгновенная мощность

Мощность:

Одинаковую работу можно совершить за разные промежутки времени. Например, можно поднять груз за минуту, а можно поднимать этот же груз в течение часа.

Физическую величину, равную отношению совершенной работы

Единицей мощности в SI является джоуль в секунду (Дж/с), или ватт (Вт), названный так в честь английского изобретателя Дж. Уатта. Один ватт — это такая мощность, при которой работу в 1 Дж совершают за 1 с. Итак,

Человек может развивать мощность в сотни ватт. Чтобы оценить, насколько могущество человеческого разума, создавшего двигатели, больше «могущества» человеческих мускулов, приведем такие сравнения:

• мощность легкового автомобиля примерно в тысячу раз больше средней мощности человека;
• мощность авиалайнера примерно в тысячу раз больше мощности автомобиля;
• мощность космического корабля примерно в тысячу раз больше мощности самолета.

Работы силы, формула

Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Рис. 1. Сила перемещает тело и совершает работу

Работа силы — это скалярное произведение вектора силы на вектор перемещения.

Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:

Векторный вид записи

\[ \large \boxed{ A = \left( \vec{F} , \vec{S} \right) }\]

Для решения задач правую часть этой формулы удобно записывать в скалярном виде:

\[ \large \boxed{ A = \left| \vec{F} \right| \cdot \left| \vec{S} \right| \cdot cos(\alpha) }\]

\( F \left( H \right) \) – сила, перемещающая тело;

\( S \left( \text{м} \right) \) – перемещение тела под действием силы;

\( \alpha \) – угол между вектором силы и вектором перемещения тела;

Работу обозначают символом \(A\) и измеряют в Джоулях. Работа – это скалярная величина.

В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.

Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.

Рассмотрим несколько случаев, следующих из формулы:

1. Когда угол между силой и перемещением острый, работа силы положительная;
2. А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
3. Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!

Внешняя скоростная характеристика (ВСХ)

Внешняя скоростная характеристика двигателя показывает зависимость мощности, расхода топлива и крутящего момента от числа оборотов коленвала. Все эти параметры показываются графически в виде кривых.

Внешняя скоростная характеристика

На рисунке можно видеть кривые с обозначениями Pe – мощность двигателя, Mе – крутящий момент, ge – удельный расход топлива. Как видно, с ростом числа оборотов и мощности увеличивается расход топлива. Крутящий момент растет до определенного уровня, а затем идет на спад. В точке, где наиболее эффективный крутящий момент и мощность двигателя, будет самый оптимальный показатель расхода топлива.

Производители моторов борются за то, чтобы максимальный крутящий момент двигатель развивал в как можно более широком диапазоне оборотов («полка крутящего момента была шире»), а максимальная мощность достигалась при оборотах, максимально приближенных к этой полке. Такой двигатель и из болота вытянет, и в городе позволяет быстро ускоряться.

Внешняя скоростная характеристика дает оценку динамическим характеристикам автомобиля, определяет КПД и топливный расход при разных параметрах.

Работа силы тяжести — разность потенциальной энергии

Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела

Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.

\( E_{p1} \left(\text{Дж} \right) \) – начальная потенциальная энергия яблока;

\( E_{p2} \left(\text{Дж} \right) \) – конечная потенциальная энергия яблока;

Примечание: Работу можно рассчитать через разность потенциальной энергии тела.

Потенциальную энергию будем вычислять, используя формулу:

\[ \large E_{p} = m \cdot g \cdot h\]

\( m \left( \text{кг}\right) \) – масса яблока;

Величина \( \displaystyle g \approx 10 \left(\frac{\text{м}}{c^{2}} \right) \) – ускорение свободного падения.

\( h \left( \text{м}\right) \) – высота, на которой находится яблоко относительно поверхности земли.

Начальная высота яблока над поверхностью земли равна 3 метрам

\[ \large E_{p2} = 0,2 \cdot 10 \cdot 3 = 6 \left(\text{Дж} \right) \]

Потенциальная энергия яблока на столе

\[ \large E_{p1} = 0,2 \cdot 10 \cdot 1 = 2 \left(\text{Дж} \right) \]

Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.

\[ \large \Delta E_{p} = E_{p2} — E_{p1} \]

\[ \large \Delta E_{p} = 2 – 6 = — 4 \left(\text{Дж} \right) \]

Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!

Чтобы работа получилась положительной, в правой части формулы перед \( \Delta E_{p}\) дополнительно допишем знак «минус».

\[ \large \boxed{ A = — \Delta E_{p} }\]

Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.

Примечания:

1. Если тело падает на землю, работа силы тяжести положительна;
2. Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
3. Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
4. Работа силы тяжести не зависит от траектории, по которой двигалось тело;
5. Работа для силы \(\displaystyle F_{\text{тяж}}\) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.

Рисунок 4 иллюстрирует факт, что для силы \(\displaystyle F_{\text{тяж}}\) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой

Приборы для измерения

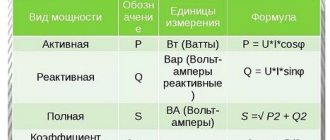
Чтобы измерить мощность, используется ваттметр, вольтметр, варметр и мультиметр с тестером. Они широко используются в различных сферах энергетики с промышленностью, связью, транспортом, наукой, медициной и бытом. В быту их используют, чтобы подсчитать потребляемую электрическую энергию и вычислить возможные повреждения диодов. Стоит отметить, что все существующие приборы для измерения делятся на щитовые с переносными и стационарными, показывающие с регистрирующими, оценивающие и сравнивающие.

Перечисленные приборы подключаются параллельным образом к нагрузке либо источнику электричества. Ваттметры с варметрами отличаются от других тем, что могут определять показатель в электромагнитно сигнале. Делятся на те, что созданы для измерений низких и высоких частот. Что касается вольтметров, они бывают аналоговыми, цифровыми, жиодно-компенсационными, импульсными, фазочувствительными и селективными.

Мультиметры являются комбинированными устройствами. Они, как и вольтметры, делятся на цифровые и аналоговые. Служат как для вычисления напряжения, так и электрической емкости с индуктивностью, температурой, силой тока и сопротивления.

Ваттметр как основной измерительный прибор для электрических приборов

Мощность

В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.

Примечание: Символ \(\vec{N}\) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

\[ \large A = \Delta E_{k} \]

\[ \large A = \Delta E_{p} \]

\[ \large A = F \cdot S \cdot cos(\alpha) \]

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

\[ \large \boxed{ P = \frac{A}{\Delta t} }\]

Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

\[ \large P = \left( \vec{F} , \vec{v} \right) \]

Формулу можно записать в скалярном виде:

\[ \large P = \left| \vec{F} \right| \cdot \left| \vec{v} \right| \cdot cos(\alpha) \]

\( F \left( H \right) \) – сила, перемещающая тело;

\( \displaystyle v \left( \frac{\text{м}}{c} \right) \) – скорость тела;

\( \alpha \) – угол между вектором силы и вектором скорости тела;

Когда векторы \(\vec{F}\) и \(\vec{v}\) параллельны, запись формулы упрощается:

\[ \large \boxed{ P = F \cdot v }\]

Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).

Номинальное количество оборотов

Еще одним ключевым показателем электромеханических характеристик двигателя является частота вращения вала. Он выражается в числе оборотов в минуту. Часто его используют в формуле мощности электродвигателя насоса, чтобы узнать его производительность. Но необходимо помнить, что показатель всегда разный для холостого хода и работы под нагрузкой. Показатель представляет физическую величину, равной количеству полных оборотов за некий промежуток времени.

Расчетная формула частоты оборотов:

n = 30 × omega ÷ pi, где:

n — частота вращения двигателя, об/мин.

Для того, чтобы найти мощность электродвигателя по формуле оборотистости вала, необходимо привести ее к расчету угловой скорости. Поэтому P = M × omega будет выглядеть следующим образом:

P = M × (2pi × n ÷ 60) = M × (n ÷ 9,55), где

t = 60 секунд.

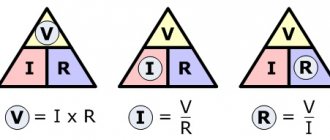
КПД

КПД – коэффициент полезного действия. Обычно обозначают греческим символом \(\eta\) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.

Примечания:

1. Процент – это дробь, у которой в знаменателе число 100.
2. КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент \(\eta\) для какого-либо устройства, механизма или процесса.

\[ \large \boxed{ \eta = \frac{ A_{\text{полезная}}}{ A_{\text{вся}}} }\]

\(\eta\) – КПД;

\( \large A_{\text{полезная}} \left(\text{Дж} \right)\) – полезная работа;

\(\large A_{\text{вся}} \left(\text{Дж} \right)\) – вся затраченная для выполнения работы энергия;

Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.

\[ \large \boxed{ \eta \leq 1 }\]

Величина \(\eta\) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:

\[ \large \boxed{ \eta = \frac{ P_{\text{полезная}}}{ P_{\text{вся затраченная}}} }\]

Конструкция электрического двигателя

Привод включает в себя:

• Ротор.
• Статор.
• Подшипники.
• Воздушный зазор.
• Обмотку.
• Коммутатор.

Ротор — единственная подвижная деталь привода, которая вращается вокруг своей оси. Ток, проходя через проводники, образует индукционное возмущение в обмотке. Формируемое магнитное поле взаимодействует с постоянными магнитами статора, что приводит в движение вал. Их рассчитывают по формуле мощности электродвигателя по току, для которой берется КПД и коэффициент мощности, в том числе все динамические характеристики вала.

Подшипники расположены на валу ротора и способствуют его вращению вокруг своей оси. Внешней частью они крепятся к корпусу двигателя. Вал проходит через них и выходит наружу. Поскольку нагрузка выходит за пределы рабочей зоны подшипников, ее называют нависающей.

Статор является неподвижным элементом электромагнитной цепи двигателя. Может включать в себя обмотку или постоянные магниты. Сердечник статора выполнен из тонких металлических пластин, которые называют пакетом якоря. Он призван снижать потери энергии, что часто происходит с твердыми стержнями.

Воздушный зазор — расстояние между ротором и статором. Эффективным является небольшой промежуток, так как он влияет на низкий коэффициент работы электродвигателя. Ток намагничивания растет с увеличением размера зазора. Поэтому его всегда стараются делать минимальным, но до разумных пределов. Слишком маленькое расстояние приводит к трению и ослаблению фиксирующих элементов.

Обмотка состоит из медной проволоки, собранной в одну катушку. Обычно укладывается вокруг мягкого намагниченного сердечника, состоящего из нескольких слоев металла. Возмущение индукционного поля происходит в момент прохождения тока через провода обмотки. В этот момент установка переходит в режим конфигурации с явными и неявными полюсами. В первом случае магнитное поле установки создает обмотка вокруг полюсного наконечника. Во втором случае, в распределенном поле рассредотачивается слотов полюсного наконечника ротора. Двигатель с экранированными полюсами имеет обмотку, которое сдерживает магнитное возмущение.

Коммутатор используют для переключения входного напряжения. Состоит из контактных колец, расположенных на валу и изолированных друг от друга. Ток якоря подается на щетки контактов ротационного коммутатора, который приводит к изменению полярности и заставляет вращаться ротор от полюса к полюсу. При отсутствии напряжения мотор прекращает крутиться. Современные установки оборудованы дополнительными электронным средствами, которые контролируют процесс вращения.

Выводы

1. Сила, приложенная к телу и перемещающая его, совершает работу;
2. Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
3. Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
4. Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
5. Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
6. Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
7. Сила тяжести — это консервативная сила. Поэтому, работа силы \(\displaystyle F_{\text{тяж}}\) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
8. Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
9. Коэффициент полезного действия обозначают греческим символом \(\eta\) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
10. КПД — это либо правильная дробь, или дробь, равная единице.
11. Можно вычислять КПД, подставляя в формулу работу, или мощности

Нагрев детали в зависимости от сопротивления

Выбирая подходящий резистор, обязательно надо обращать внимание на температурный диапазон, при котором возможна корректная эксплуатация детали. Она всегда указывается изготовителем

Чтобы резистор не вышел из строя, необходим своевременный выход теплоты в атмосферу. Элемент не должен перегреваться. Чем холоднее воздух (в рамках допустимого диапазона), тем дольше имеет шанс прослужить компонент. Нельзя позволять, чтобы поблизости от резистора скапливалось избыточное тепло.

Когда температурный показатель достигает своего максимума в рамках диапазона, на сопротивлении начинается процесс выгорания верхнего маркируемого слоя. В таком случае необходимо принимать меры по снижению температуры, иначе у изделия выгорит наполнение, отвечающее за сопротивляемость, и оно станет полностью непригодным к дальнейшей эксплуатации.

Если детали с требуемой размерностью под конкретную схему не обнаружилось, можно использовать вариант с превосходящим значением, если он подходит собираемому устройству. Резисторы, чьи данные по мощности не дотягивают до требуемых, применять в такой ситуации допустимо, только объединив их последовательно. Вообще знание эффектов параллельно и последовательно связанных резисторных элементов пригодится в ситуации, если под рукой не оказалось детали с идеально подходящими параметрами.