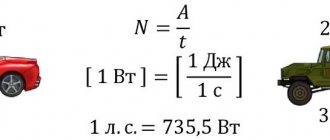- Example No. 3
Power:
The same work can be done in different periods of time. For example, you can lift a load in a minute, or you can lift the same load for an hour.
A physical quantity equal to the ratio of work done
The SI unit of power is the joule per second (J/s), or watt (W), named after the English inventor J. Watt. One watt is the power at which 1 J of work is done in 1 s. So,
A person can develop power of hundreds of watts. To evaluate how much the power of the human mind, which created the engines, is greater than the “power” of human muscles, let us give the following comparisons:
- the power of a passenger car is approximately a thousand times greater than the average power of a person;
- The power of an airliner is approximately a thousand times greater than that of a car;
- The power of a spacecraft is approximately a thousand times greater than that of an airplane.
Work of force, formula
A force applied to a body and moving it does work (Fig. 1).
Rice. 1. Force moves a body and does work
The work of a force is the scalar product of the force vector and the displacement vector.
The work done by a force can be calculated using a vector or scalar form of writing the following formula:
Vector record view
\[ \large \boxed{ A = \left( \vec{F} , \vec{S} \right) }\]
To solve problems, it is convenient to write the right side of this formula in scalar form:
\[ \large \boxed{ A = \left| \vec{F} \right| \cdot \left| \vec{S} \right| \cdot cos(\alpha) }\]
\( F \left( H \right) \) – force moving the body;
\( S \left( \text{м} \right) \) – movement of the body under the influence of force;
\( \alpha \) – the angle between the force vector and the body displacement vector;
Work is denoted by the symbol \(A\) and measured in Joules. Work is a scalar quantity.
In the case where the force is constant, the formula allows you to calculate the work done by the force during the total time of its action.
If the force changes with time, then at each specific moment in time we will receive instantaneous work. These instantaneous values will differ for different points in time.
Let's consider several cases following from the formula:
- When the angle between force and displacement is acute, the work done by the force is positive;
- And if the angle is obtuse, the work is negative, since the cosine of an obtuse angle is negative;
- If the angle is right, the work is zero. A force perpendicular to the displacement does no work!
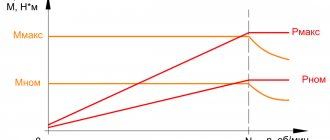
External speed characteristic (VSCH)
The external speed characteristic of the engine shows the dependence of power, fuel consumption and torque on the crankshaft speed. All these parameters are shown graphically in the form of curves.
External speed characteristic
In the figure you can see curves with the designations Pe - engine power, Me - torque, ge - specific fuel consumption. As you can see, with increasing speed and power, fuel consumption increases. The torque increases to a certain level and then decreases. At the point where the engine torque and power are most efficient, there will be the most optimal fuel consumption.
Motor manufacturers are fighting to ensure that the engine develops maximum torque in the widest possible speed range (“the torque plateau is wider”), and maximum power is achieved at speeds as close as possible to this shelf. Such an engine will pull you out of the swamp and allow you to accelerate quickly in the city.
The external speed characteristic evaluates the dynamic characteristics of the car, determines efficiency and fuel consumption for different parameters.
Work done by gravity - potential energy difference
Let's now consider the following example. An apple weighing 0.2 kg fell onto a garden table from a branch located at a height of 3 meters from the surface of the earth. The tabletop is located at a height of 1 meter from the surface (Fig. 3). Let's find the work done by gravity in this process.
Rice. 3. The figure shows the initial 1st position of the body (apple) and its final 2nd position, marked heights for calculating the work of vertical movement of the body
Let's calculate the potential energy of the apple before it falls and the energy of the apple on the table top.
\( E_{p1} \left(\text{J} \right) \) – initial potential energy of the apple;
\( E_{p2} \left(\text{J} \right) \) – final potential energy of the apple;
Note: Work can be calculated through the difference in the potential energy of the body.
We will calculate potential energy using the formula:
\[ \large E_{p} = m \cdot g \cdot h\]
\( m \left( \text{kg}\right) \) – mass of the apple;
The quantity \( \displaystyle g \approx 10 \left(\frac{\text{m}}{c^{2}} \right) \) is the acceleration of free fall.
\( h \left( \text{m}\right) \) – the height at which the apple is located relative to the surface of the earth.
The initial height of the apple above the ground is 3 meters
\[ \large E_{p2} = 0.2 \cdot 10 \cdot 3 = 6 \left(\text{J} \right) \]
Potential energy of an apple on the table
\[ \large E_{p1} = 0.2 \cdot 10 \cdot 1 = 2 \left(\text{J} \right) \]
Now let's find the difference in the potential energy of the apple at the end of the fall and before it begins.
\[ \large \Delta E_{p} = E_{p2} — E_{p1} \]
\[ \large \Delta E_{p} = 2 – 6 = — 4 \left(\text{J} \right) \]
It is important to remember: When a body falls to the ground, its potential energy decreases. The force of gravity does positive work!
To make the work positive, we will additionally add a minus sign on the right side of the formula before \( \Delta E_{p}\).
\[ \large \boxed{ A = — \Delta E_{p} }\]
This means that the work required by gravity for an apple weighing 0.2 kg to fall from a height of 3 m to a height of 1 meter is equal to 4 Joules.
Notes:
- If a body falls to the ground, the work done by gravity is positive;
- When we lift a body above the ground, we do work against gravity. Our work is positive, and the work of gravity will be negative;
- Gravity is a conservative force. For conservative forces, we add a minus sign in front of the potential energy difference;
- The work done by gravity does not depend on the trajectory along which the body moved;
- The work for the force \(\displaystyle F_{\text{heavy}}\) depends only on the difference in heights at which the body was at the final and initial moments of time.
Figure 4 illustrates the fact that for the force \(\displaystyle F_{\text{heavy}}\) the work depends only on the difference in height and does not depend on the trajectory along which the body moved.
Rice. 4. The height difference between the initial and final position of the body in all cases in the figure is the same, therefore, the work of gravity for the presented cases will be the same
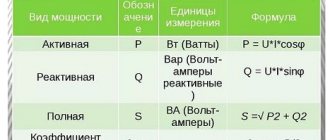
Measuring instruments
To measure power, a wattmeter, voltmeter, varmeter and multimeter with tester are used. They are widely used in various fields of energy with industry, communications, transport, science, medicine and everyday life. In everyday life, they are used to calculate the electrical energy consumed and calculate possible damage to the diodes. It is worth noting that all existing measuring instruments are divided into panel with portable and stationary, indicating with recording, evaluating and comparing.
The listed devices are connected in parallel to the load or source of electricity. Wattmeters with varmeters differ from others in that they can determine an indicator in an electromagnetic signal. They are divided into those designed for measuring low and high frequencies. As for voltmeters, they are analog, digital, liquid-compensated, pulse, phase-sensitive and selective.
Multimeters are combined devices. They, like voltmeters, are divided into digital and analog. They are used to calculate both voltage and electrical capacitance with inductance, temperature, current and resistance.
Wattmeter as the main measuring instrument for electrical appliances
Power
In mechanics, power is often symbolized N or P and measured in Watts, after the Scottish inventor James Watt.
Note: The symbol \(\vec{N}\) is used to denote the ground reaction force - it is measured in Newtons and is a vector quantity. To avoid confusion, we will denote power instead of N by the symbol P. The symbol P is the first letter in the English word power.
Power is work done in one second (energy expended in 1 second).
We calculate the work using any of the formulas:
\[ \large A = \Delta E_{k} \]
\[ \large A = \Delta E_{p} \]
\[ \large A = F \cdot S \cdot cos(\alpha) \]
Dividing this work by the time during which it was performed, we get the power.
\[ \large \boxed{ P = \frac{A}{\Delta t} }\]
If the work was done in equal parts at equal time intervals, the power will be a constant value.
Power is variable when more work is done at some time intervals.
Another formula for calculating power
There is another way to calculate power, when a force moves a body and the speed of the body does not change:
\[ \large P = \left( \vec{F} , \vec{v} \right) \]
The formula can be written in scalar form:
\[ \large P = \left| \vec{F} \right| \cdot \left| \vec{v} \right| \cdot cos(\alpha) \]
\( F \left( H \right) \) – force moving the body;
\( \displaystyle v \left( \frac{\text{m}}{c} \right) \) – body speed;
\( \alpha \) – the angle between the force vector and the body velocity vector;
When the vectors \(\vec{F}\) and \(\vec{v}\) are parallel, the formula is simplified:
\[ \large \boxed{ P = F \cdot v }\]
Note: This formula for calculating power can be obtained from the expression for the work of force by dividing both sides of this expression by the time during which the work was performed (or more precisely, by finding the derivative of both sides of the equation).
Nominal speed
Another key indicator of the electromechanical characteristics of the engine is the shaft speed. It is expressed in revolutions per minute. It is often used in the pump motor power formula to find out its performance. But it must be remembered that the indicator is always different for idling and operation under load. The indicator represents a physical quantity equal to the number of full revolutions over a certain period of time.
Calculation formula for speed:
n = 30 × omega ÷ pi, where:
n — engine speed, rpm.
In order to find the power of an electric motor using the shaft speed formula, it is necessary to reduce it to the calculation of angular velocity. Therefore P = M × omega will look like this:
P = M × (2pi × n ÷ 60) = M × (n ÷ 9.55), where
t = 60 seconds.
Efficiency
Efficiency – efficiency factor. Usually denoted by the Greek symbol \(\eta\) "this". It has no units of measurement and is expressed either as a decimal fraction or as a percentage.
Notes:
- A percentage is a fraction whose denominator is 100.
- Efficiency is either a proper fraction or a fraction equal to unity.
Calculate the coefficient \(\eta\) for a device, mechanism or process.
\[ \large \boxed{ \eta = \frac{ A_{\text{useful}}}{ A_{\text{all}}} }\]
\(\eta\) – efficiency;
\( \large A_{\text{useful}} \left(\text{J} \right)\) – useful work;
\(\large A_{\text{all}} \left(\text{J} \right)\) – all the energy expended to perform the work;
Note: Efficiency is often less than unity, since there is always energy loss. The efficiency cannot be greater than one, since this contradicts the law of conservation of energy.
\[ \large \boxed{ \eta \leq 1 }\]
The quantity \(\eta\) is a fractional quantity. If the numerator and denominator of a fraction are divided by the same number, the resulting fraction will be equal to the original. Using this fact, you can calculate efficiency using power:
\[ \large \boxed{ \eta = \frac{ P_{\text{useful}}}{ P_{\text{all spent}}} }\]
Electric motor design
Drive includes:
- Rotor.
- Stator.
- Bearings.
- Air gap.
- Winding.
- Switch.
The rotor is the only moving part of the drive that rotates around its axis. The current passing through the conductors forms an inductive disturbance in the winding. The generated magnetic field interacts with the permanent magnets of the stator, which causes the shaft to move. They are calculated using the formula for electric motor power by current, for which the efficiency and power factor are taken, including all the dynamic characteristics of the shaft.
Bearings are located on the rotor shaft and contribute to its rotation around its axis. The outer part is attached to the engine housing. The shaft passes through them and comes out. Since the load extends beyond the working area of the bearings, it is called overhanging.
The stator is a stationary element of the electromagnetic circuit of the engine. May include winding or permanent magnets. The stator core is made of thin metal plates called the armature package. It is designed to reduce energy loss, which often occurs with solid rods.
Air gap is the distance between the rotor and stator. A short gap is effective, as it affects the low efficiency of the electric motor. The magnetizing current increases with increasing gap size. Therefore, they always try to make it minimal, but to reasonable limits. Too small a distance leads to friction and weakening of the fixing elements.
The winding consists of copper wire assembled into one coil. Typically laid around a soft magnetized core consisting of several layers of metal. The induction field is disturbed when current passes through the wires of the winding. At this point, the installation enters configuration mode with explicit and implicit poles. In the first case, the magnetic field of the installation is created by a winding around the pole piece. In the second case, the slots of the rotor pole piece are dispersed in the distributed field. A shaded pole motor has a winding that inhibits magnetic disturbance.
The switch is used to switch the input voltage. It consists of slip rings located on the shaft and isolated from each other. The armature current is supplied to the contact brushes of the rotary commutator, which causes a change in polarity and causes the rotor to rotate from pole to pole. If there is no voltage, the motor stops turning. Modern installations are equipped with additional electronic means that control the rotation process.
conclusions
- A force applied to a body and moving it does work;
- When the angle between the force and the displacement is acute, the work of the force is positive, and if the angle is obtuse, the work is negative; If the angle is right, the work is zero. A force perpendicular to the displacement does no work!
- Work can be calculated by measuring the kinetic energy of a body at the beginning and end of its motion;
- The work can be calculated through the difference in the potential energy of the body at the initial and final heights above the ground;
- When a body falls to the ground, its potential energy decreases. The force of gravity does positive work!
- We do work against gravity when we lift our body above the ground. Moreover, our work is positive, and the work of gravity is negative;
- Gravity is a conservative force. Therefore, the work of force \(\displaystyle F_{\text{heavy}}\) does not depend on the trajectory along which the body moved, but depends only on the difference in heights at which the body was at the final and initial moments of time;
- Power is work done in one second, or expended in 1 second. energy;
- The efficiency factor is denoted by the Greek symbol \(\eta\) “eta”, has no units of measurement, and is expressed either as a decimal fraction or as a percentage;
- Efficiency is either a proper fraction or a fraction equal to unity.
- You can calculate efficiency by substituting work or power into the formula
Part heating depending on resistance
When choosing a suitable resistor, you must pay attention to the temperature range at which correct operation of the part is possible. It is always specified by the manufacturer
In order for the resistor not to fail, timely release of heat into the atmosphere is necessary. The element must not overheat. The colder the air (within the acceptable range), the longer the component has a chance to last. Do not allow excess heat to accumulate near the resistor.
When the temperature indicator reaches its maximum within the range, the process of burning out the upper marked layer begins at the resistance. In this case, it is necessary to take measures to reduce the temperature, otherwise the product’s filling, which is responsible for resistance, will burn out and it will become completely unsuitable for further use.
If a part with the required dimension for a specific circuit is not found, you can use the option with a superior value if it suits the device being assembled. Resistors whose power data does not reach the required ones can be used in such a situation only by combining them in series. In general, knowledge of the effects of parallel and series connected resistor elements will be useful in a situation where there is no part with ideally suitable parameters at hand.