- How is potential difference determined? How are the strength of a uniform electrostatic field and potential difference related?
Work to move a charge in an electrostatic field:
In everyday life, we quite often, especially in dry weather, encounter a situation where, having touched a body, we feel an unpleasant blow. Experience shows that such surprises can be expected from bodies with high potential.
Work of the electrostatic field
Let's consider the situation: charge q0 enters an electrostatic field. This electrostatic field is also created by some charged body or system of bodies, but we are not interested in this. A force acts on the charge q0 from the field, which can do work and move this charge in the field.
The work of the electrostatic field does not depend on the trajectory. The work done by the field when a charge moves along a closed path is zero. For this reason, the electrostatic field forces are called conservative
, and the field itself is called
potential
.
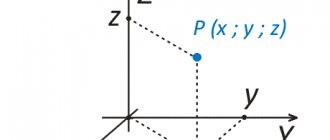
Let a point charge `q` be in a uniform electric field with intensity `vecE`. (For a generalization to the case of an inhomogeneous field, see below.) Then the force `vecF=qvecE` acts on it from the field. Let's consider the movement of this charge from point `1`, characterized by the radius vector `vecr_1`, to point `2` - with the radius vector `vecr_2` along, generally speaking, a curvilinear trajectory (Fig. 11). Let's mentally divide the entire trajectory into a large number of small movements `Deltavecr_i`, so that `Deltavecr=vecr_2-vecr_1=sum_i Deltavecr_i`, where we consider all vectors `Deltavecr_i` to be added according to the polygon rule.
The work of force on the part of the electric field when moving charge `q` from point `1` to point `2` is called the quantity (the sum of work in individual areas)
`A_(12)=sum_i vecF_i Deltavecr_i`, (1.4.1.)
where `vecF_i` is the force acting on the charge in a small area `Deltavecr_i`, `vecF_iDeltavecr_i` is the scalar product of vectors. In our case (uniform electric field), the force in all areas is the same, `vecF=qvecE`, so we get
`A_(12)=sum_i vecF_i Deltavecr_i= qvecE sum_i Deltavecr_i=qvecE(vecr_2-vecr_1)`. (1.4.2)
Note that the work of the electrostatic field force (1.4.2) is determined only by the starting and ending points (two radius vectors `vecr_1` and `vecr_2`) and does not depend on the specific trajectory along which the charge moved (the answer included only the difference of these vectors ). Forces that have the property that the work of these forces does not depend on the trajectory are called conservative forces, and the corresponding fields are called potential fields. Not all forces have this property; An example of a non-conservative force is the friction force. Another important example of a non-potential field (and a non-conservative force) is an electric field that varies with time.
According to the general theorem of mechanics, the change in the kinetic energy of a charge is equal to the sum of the work done by all forces :
`(mv_2^2)/2 — (mv_1^2)/2 =A_(12)^(“with all our might”)`. (1.4.3)
If the charge moved only under the influence of the electric field forces (there were no strings for which we would pull the charge, there was no friction force, etc.), then instead of (1.4.3) (and according to (1.4.2)) we have:
`(mv_2^2)/2 — (mv_1^2)/2 =qvecE(vecr_2-vecr_1)`. (1.4.4)
Let us rewrite the last equality in the form
`(mv_2^2)/2 -qvecEvecr_2= (mv_1^2)/2-qvecEvecr_1`, (1.4.4′)
which allows for the following important interpretation. Let's say that charge `q` in a uniform electrostatic field has potential energy
`Pi(vecr)=-qvecEvecr+Pi_0`, (1.4.5)
where `Pi_0` is an arbitrary constant. Then, taking into account the fact that `K=(mv^2)/2` is the kinetic energy of the charge, equality (1.4.4') is simply the law of conservation of energy :
`K_2+Pi_2=K_1+Pi_1`, (1.4.6)
i.e., during the process of movement, the sum of kinetic and potential energies does not change (retains its value).
If we assign a potential energy equal to zero to the point `A` with the radius vector `vecr_0`, then this is equivalent to choosing the constant `Pi_0=+qvecEvecr_0`. Choosing the origin `(vecr_0=0)` as the point `A`, we obtain `Pi_0=0` and `Pi(vecr)=-qvecEr`.
The most important concept in the study of electricity is potential . Let us rewrite the expression for the work of electrostatic field forces in the form
`A_(12)=qvecE(vecr_2-vecr_1)=Pi_1-Pi_2=q(varphi_1-varphi_2)`, (1.4.7)
introducing the potential of a uniform electrostatic field according to the formula
`varphi(vecr)=-vecEvecr+varphi_0`, (1.4.8)
`varphi_0` is an arbitrary constant.
Having written (1.4.8) in the form `varphi(vecr)=-(+1)vecEvecr+varphi_0`, we can purely formally (in accordance with (1.4.5)) interpret the potential as the potential energy of a unit positive charge `(+1) ` in an electric field. It is important to remember, however, that potential and potential energy have different dimensions. Due to equality (1.4.7) and, accordingly,
`varphi=Pi//q`, (1.4.9)
potential is measured in units of J/C = V (volts).
Using formula (1.4.8), we also find the change in potential when moving from one point of the field to another - with the radius vectors `vecr_1` and `vecr_2`:
`Deltavarphi=varphi_2-varphi_1=varphi(vecr_2)-varphi(vecr_1)=-vecE(vecr_2-vecr_1)=-vecEDeltavecr`. (1.4.10)
Note that if the movement is perpendicular to the electric field, `Deltavecr_|_vecE`, then the scalar product `vecEDeltavecr=0`, i.e. `Deltavarphi=0`: moving in the plane perpendicular to the electric field strength vector `vecE`, we move from one point to another with the same potential. Such planes (in the general case, surfaces) are spoken of as equipotential surfaces.
How will the potential change when moving from one equipotential plane to another? Let's consider movement along the electric field `Deltavecr«||«vecE`. Let's direct the `X` axis parallel to the electric field (not necessarily along the field, maybe, and against the field, so the projection `E_x` of the `vecE` vector onto the `X` axis can have any sign). According to the basic properties of the scalar product of vectors `(vecavecb=|veca|*|vecb|cosalpha=a_xb_x+a_yb_y+a_zb_z)` we have
`varphi(x)=-E_x+varphi_0`, (1.4.8′)
and for potential increase
`Deltavarphi=varphi_2-varphi_1=varphi(x_2)-varphi(x_1)=-E_x(x_2-x_1)=-E_xDeltax`. (1.4.10′)
Formula (1.4.10') can be given the following form. Let the `X` axis be directed along the field `(E=E_x>0)` and let `d=x_2-x_1`. Let's enter the potential difference (voltage) using the formula `U=varphi_1-varphi_2`. Then according to (1.4.10') we obtain `U=Ed`.
Example 13
Determine the potential difference between two uniformly charged planes parallel to each other, one of which is positively charged with surface density `sigma_1=+sigma`, and the second negatively `sigma_2=-sigma`. The distance between the planes is `d`. Define also:
1) what will the potential of the 2nd plane be equal to if the potential of the 1st plane is taken equal to zero?
2) What will be the potential of the 1st plane if we take the potential of the 2nd plane as zero potential?
Solution
Let's direct the `X` axis from the 1st plane to the 2nd perpendicular to both of them and align the origin of coordinates with the 1st plane. Then `U=Ed=sigma/(epsilon_0)d`.
1) Assuming `varphi(x)=-E_x x+varphi_0`, (1.4.8′) `varphi(0)=0` in the formula, we obtain `varphi_0=0` and `varphi(d)=-U`.
2) In this case, put in (1.4.8′) `varphi(d)=0`, then `varphi_0=U` and `varphi(0)=+U`.
Example 14
The accelerating voltage in the cathode ray tube of the TV picture tube is `U=30` kV. To what speed do electrons accelerate in it? What percentage does it make of the speed of light in vacuum `c=3*10^8` m/s. The initial speed of the electron is zero. Electron mass `m=0.91*10^(-30)` kg.
Solution
Let's use the law of conservation of energy:
`Delta(mv^2//2)=|DeltaPi|=eU`,
from where we get `v=sqrt((2eU)/m)~~103000` km/s `~~0.34` s (i.e. it is `34%` of the speed of light).
So far we have considered only a uniform electrostatic field. The simplest example of a non-uniform field is the field of a point charge . Unfortunately, finding the work of forces even in this relatively simple field without involving higher mathematics is very difficult. Therefore, we present the formula for it without derivation.
Let there be a stationary point charge `q` and let another charge `q_0` move in the field of this charge. Let it move from point `1`, characterized by the radius vector `vecr_1`, to point `2` - with the radius vector `vecr_2` along, generally speaking, a curvilinear trajectory. It can be shown (the conclusion can be found in the book `[3]`) that in this case the work of the electrostatic field forces will be equal to
`A_(12)=(q_0q)/(4pi epsilon_0r_1) — (q_0q)/(4pi epsilon_0r_2)`, (1.4.11)
where `r_1=|vecr_1|`, `r_2=|vecr_2|`. Next we proceed as in the case of a homogeneous field. If during the movement of the charge `q_0` no other forces acted except the Coulomb force on the side of the charge `q`, then according to the theorem on the change in kinetic energy we have:
| `(mv_2^2)/2-(mv_1^2)/2=(q_0q)/(4pi epsilon_0r_1)-(q_0q)/(4pi epsilon_0r_2)`, | |
| or else | |
| `(mv_2^2)/2+(q_0q)/(4pi epsilon_0r_2)= (mv_1^2)/2+(q_0q)/(4pi epsilon_0r_1)` | (1.4.12) |
Determining the potential energy of interaction of point charges `q` and `q_0` located at a distance `r` from each other, by the formula
`Pi(r)=(q_0q)/(4pi epsilon_0r)+Pi_0`, (1.4.13)
where `Pi_0` is an arbitrary constant, we can give equality (1.4.12) the form of the law of conservation of energy `K_2+Pi_2=K_1+Pi_1`.
In the case of point charges, quite often the constant `Pi_0` is chosen equal to zero so that the potential energy of interaction between two charges tends to zero when the charges are separated by an infinitely large distance from each other (when they stop “feeling” each other). In this case
`Pi(r)=(q_0q)/(4pi epsilon_0r)`. (1.4.13′)
Let different test charges `q_1`, `q_2`, `…` be alternately placed at the same point in the field of a point charge `q` at a distance `r` from it. The energies of these charges will be different `Pi_1`, `Pi_2`, `…`. It is important, however, that the ratio of these energies to the values of the test charges will be the same
`(Pi_1(r))/(q_1)=(Pi_2(r))/(q_2)=…=q/(4pi epsilon_0r)-=varphi(r)`. (1.4.14)
The last equality determines the potential `varphi(r)` of a point charge `q` at a distance `r` from it. Note that according to (1.4.11), the potential `varphi(r)=q/(4pi epsilon_0r)` is equal to the work of the forces of the electrostatic field of the charge `q` when moving a unit positive point charge from a point at a distance `r` from the charge `q` to infinity. Potential, like potential energy, is defined, generally speaking, ambiguously - up to an arbitrary constant
`varphi(r)=q/(4pi epsilon_0r)+varphi_0`, (1.4.14′)
which is very often chosen to be equal to zero so that when moving away from the charge to an infinitely large distance, the potential of the charge at these (infinitely distant points) tends to zero.
According to formula (1.4.14′), the potential of a point charge is the same at all points equidistant from it. This means that the equipotential surfaces in this case will be concentric spheres. As in the case of a uniform field, at each point of the field the intensity is perpendicular to the equipotential surface.
If an electrostatic field is created by several charges `q_1,q_2,…`, the potential at an arbitrary point in the field is equal to the sum of the potentials created by each of the charges at that point:
`varphi=varphi_1+varphi_2+…`, (1.4.15)
which, as in the case of field strengths, is called the principle of superposition. It is important that the field strengths must be added vectorially , and the potentials - algebraically (that is, still taking into account the signs).
Example 15
If a balloon with a radius of `R=10` cm is rubbed on wool, fur or hair, it will acquire a fairly large negative charge - on the order of `q=0.1` µC. What will be the potential of the ball?
Solution
The field outside the ball coincides with the field of a point charge. The ball's potential will be equal to
`varphi=1/(4pi epsilon_0) q/R=9000` V,
i.e. almost `10` kilovolts (!). A natural question arises: haven’t we received too many volts here? Is there a mistake in our assessment? No, we are not wrong. Despite such impressive potential, the ball will have very little energy. The energy of a balloon can be estimated using the formula `W=(1//2)qvarphi`, which we will present without derivation, which gives `W~~10.5*10^(-3)` J, so all these `9` Thousands of volts do not pose any real danger.
Example 16
In the case of the movement of individual elementary particles (electrons, protons), a convenient unit of energy measurement is the electron volt (eV). This is the name given to the energy acquired by a particle with a charge equal to the elementary electric charge after passing through a potential difference of `1` volt. The electron energy in a hydrogen atom is `W=-13.6` eV. Assuming that the electron in the hydrogen atom moves in a circular orbit, find the radius of this orbit.
Solution
The electron energy consists of kinetic and potential: `W=(mv^2)/2-(e^2)/(4pi epsilon_0r)`. Let's write down Newton's 2nd law for the motion of an electron in the field of a proton: `(mv^2)/r=(e^2)/(4pi epsilon_0r^2)`, from which we get `(mv^2)/2=1/ 2 (e^2)/(4pi epsilon_0r)` and `W=-1/2 (e^2)/(4pi epsilon_0r)`. Solving this equation for `r`, after substituting the numerical values we find `r=0.53*10^(-10)` m.
The two main objects of our further study are conductors and dielectrics in an electric field, as well as electric fields in a vacuum in their presence. It is believed that conductors contain a large number of mobile charge carriers (able to move freely within the conductor). In dielectrics, on the contrary, it is believed that there are practically no such mobile charges (their number is negligible).
Potential
The "charge - electrostatic field" or "charge - charge" system has potential energy, just as the "gravitational field - body" system has potential energy.
A physical scalar quantity characterizing the energy state of the field is called potential
a given point in the field. A charge q is placed in a field, it has potential energy W. Potential is a characteristic of an electrostatic field.
Let's remember potential energy in mechanics. Potential energy is zero when the body is on the ground. And when a body is raised to a certain height, it is said that the body has potential energy.
Regarding potential energy in electricity, there is no zero level of potential energy. It is chosen randomly. Therefore, potential is a relative physical quantity.
In mechanics, bodies tend to occupy a position with the least potential energy. In electricity, under the influence of field forces, a positively charged body tends to move from a point with a higher potential to a point with a lower potential, and a negatively charged body, vice versa.
Potential field energy is the work done by the electrostatic force when moving a charge from a given point in the field to a point with zero potential.
Let us consider the special case when an electrostatic field is created by an electric charge Q. To study the potential of such a field, there is no need to introduce a charge q into it. You can calculate the potential of any point in such a field located at a distance r from the charge Q.
The dielectric constant of the medium has a known value (tabular) and characterizes the medium in which the field exists. For air it is equal to unity.
Literature
- Aksenovich L. A. Physics in secondary school: Theory. Tasks. Tests: Textbook. allowance for institutions providing general education. environment, education / L. A. Aksenovich, N. N. Rakina, K. S. Farino; Ed. K. S. Farino. - Mn.: Adukatsiya i vyakhavanne, 2004. - P. 228-233.
- Zhilko, V.V. Physics: textbook. allowance for 11th grade. general education institutions with Russian language training with a 12-year period of study (basic and advanced levels) /V. V. Zhilko, L. G. Markovich. — 2nd ed., revised. — Minsk: Nar. Asveta, 2008. - pp. 86-95.
How to determine the sign of potential
When solving problems, a lot of confusion arises when determining the sign of potential, potential difference, and work.
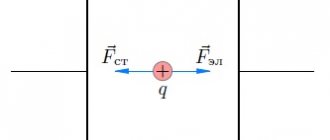
The figure shows tension lines. At which point in the field is the potential greater?
The correct answer is point 1. Let us remember that the tension lines begin on a positive charge, which means the positive charge is on the left, therefore the leftmost point has the maximum potential.
If a field is being studied that is created by a negative charge, then the field potential near the charge has a negative value; this can be easily verified if a charge with a minus sign is substituted into the formula. The further away from the negative charge, the greater the field potential.
If a positive charge moves along the tension lines, then the potential difference and work are positive. If a negative charge moves along the tension lines, then the potential difference has a “+” sign, and the work has a “-” sign.
Think for yourself: the work and potential difference will take negative or positive values if the charge is moved in the opposite direction relative to the tension lines.
Forces and their action on a charged particle
A charged electron is subject to a force with some acceleration, causing it to move faster and faster. This force does work to move the electron.
Lines of force are imaginary shapes that appear around charges (determined by the electric field) and if we place any charge in that area, it will experience a force.
Properties of power lines:
- travel from north to south;
- have no mutual intersections.
Why don't two lines of force intersect? Because this doesn't happen in real life. What is being said is a physical model and nothing more. Physicists invented it to describe the behavior and characteristics of the electric field. The model is very good at this. But remembering that this is just a model, we must know why such lines are needed.
Lines of force show:
- directions of electric fields;
- tension. The closer the lines, the greater the field strength and vice versa.
If the drawn force lines of our model intersect, the distance between them will become infinitesimal. Because of the strength of the field as a form of energy, and because of the fundamental laws of physics, this is impossible.
4. The concept of circulation
Let there be a vector field in some region of space.
| The circulation of a vector along an arbitrary closed contour L is the following curvilinear integral: |
Here is a unit vector tangent to the contour at a given point, directed towards the positive bypass of the contour.
There is a convention that the positive direction of traversing a contour (direction ) is chosen such that the area covered by the contour remains on the left when traversing.
Let us briefly recall how a curvilinear integral can be “constructed.” To do this, you need to select a point on the contour, show the vector at it, at the same point show the unit tangent vector, calculate the scalar product, break the contour into small elements, designate the length of the element, calculate the product; do this for all contour elements; sum the results, directing the element of the contour length to zero - move from summation to integration.
Just like flow, circulation is another characteristic of the properties of a vector field. Namely, circulation characterizes the degree of vorticity of the vector field.
Example:
If you can take a turbine as a “meter” of the circulation of the fluid velocity field, then if it rotates, the circulation is not zero.
Circulation
is an integral characteristic of the field.
Plan:
| 1.Work of the electric field. |
| 2.Work in the field of a point charge. |
| 3.Circulation theorem. |
| 4. The concept of circulation. |
| 5. The concept of a rotor. |
| 6. Stokes formula. |
| 7.Expression for the rotor in the Cartesian coordinate system. |
| 8.Circulation and rotor in electrostatics. |
| 9. Potential energy. |
| 10.Potential difference. |
| 11. Unit of potential difference. |
| 12.Point charge potential. |
5. Concept of rotor
The structure of the field can be quite heterogeneous. Circulation does not provide a detailed description of the field. Consequently, we begin to contract the integration contour to some point M
(reduce turbine). In this case, the circulation will tend to zero, but the area covered by the contour will also tend to zero. And their ratio gives a finite number.
The turbine can be oriented in space in three independent ways. Therefore, in this way you can get 3 independent numbers, and three numbers are a vector, therefore, a vector characteristic of the field is formed, which is called a rotor.
Rotor
is a local or differential characteristic.