Как найти эквивалентное сопротивление цепи формула

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).

На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I1 + I2 + I3, т.е. ,

откуда следует, что

В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением

Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

Отсюда следует, что

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно

Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

Рис. 1.10

Рис. 1.11

В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

; ; .

После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

Электрическая цепь с последовательным соединением элементов

Рис. 1.4

Рис. 1.5

Электрическая цепь с параллельным соединением элементов

I = I1 + I2 + I3, т.е. ,

откуда следует, что

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

Отсюда следует, что

т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

Электрическая цепь со смешанным соединением элементов

В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:

Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

Рис. 1.10

Рис. 1.11

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

Рис. 1.12

Рис. 1.13

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

; ; .

Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.).

Определение эквивалентного сопротивления

При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.

Резистивные электрические цепи и методы их расчета

Содержание:

Введение.

Глава 1. Электрическая цепь: основные понятия и определения.

Глава 2. Методы расчета простых резистивных цепей.

Глава 3. Расчет резистивных электрических цепей методом токов ветвей.

Глава 4. Метод узловых напряжений (МУН).

Заключение.

Используемая литература

Глава 1. Электрическая цепь: основные понятия и определения.

Электромагнитные процессы, протекающие в электротехнических устройствах, как правило, достаточно сложны. Однако во многих случаях, их основные характеристики можно описать с помощью таких интегральных понятий, как: напряжение, ток, электродвижущая сила (ЭДС). При таком подходе совокупность электротехнических устройств, состоящую источников и приемников электрической энергии, предназначенных для генерации, передачи, распределения и преобразования электрической энергии и (или) информации, рассматривают как электрическую цепь. Таким образом, электрическая цепь состоит из отдельных элементов (частей, объектов), соединенных соответствующим образом и выполняющих определенные функции. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками (потребителями) электрической энергии.

У каждого элемента цепи можно выделить определенное число зажимов (полюсов), с помощью которых он соединяется с другими элементами. К двухполюсным элементам, имеющим два зажима, относятся: большинство источников энергии, резисторы, катушки индуктивности, конденсаторы. Из многополюсных элементов наиболее распространены триоды, трансформаторы, усилители и т.д.

Большинство электрических цепей электротехнических устройств моделируют, используя базовые идеальные двухполюсные элементы, каждая из которых описывает в количественном отношении какую-либо одну из сторон реального электромагнитного процесса. Далее будут подробно изучаться такие базовые элементы, как: резистивный, индуктивный и емкостный элементы, источники сигналов, идеальный ключ и идеальный проводник.

Все элементы электрической цепи условно можно разделить на активные и пассивные. Активный элемент обязательно содержит в своей структуре источник электрической энергии. Пассивными являются элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики. Если характеристики этих элементов описываются линейными уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Строго говоря, все элементы являются нелинейными. Однако в определенных пределах изменения переменных указанных характеристик и частот электрических сигналов можно некоторые элементы рассматривать как линейные, что существенно упрощает математическое описание и анализ процессов электрической цепи. Коэффициенты, связывающие переменные, их производные и интегралы в уравнениях элементов, называются параметрами элемента.

Цепи, содержащие только линейные элементы, называются линейными. При наличии в схеме хотя бы одного нелинейного элемента цепь считается нелинейной.

Любой элемент электрической цепи характеризуется скалярными алгебраическими величинами, которые в общем случае произвольными функциями времени , в том числе: электрическим зарядом , потокосцеплением , током и напряжением , однако в практических электротехнических задачах чаще всего используют в качестве переменных только токи и напряжения , что объясняется относительным удобством физических измерений этих величин.

Электрический ток определяется как отношение:

, (1.1)

где , , ,

а электрическое напряжение – как разность:

, (1.2)

где и − электрические потенциалы точек (полюсов) 1 и 2 соответственно, , (рис.1.1).

Рис.1.1. Ток и напряжение элемента электрической цепи

Знаки тока и напряжения зависят от условно выбранных на схеме положительных направлений. Направления указываются на схеме соответствующими стрелками. Различают согласованные направления и несогласованные. При согласованных направлениях тока и напряжения их стрелки совпадают.

Если электрическое напряжение определить как работу в электрическом поле:

то отсюда можно получить соотношение для мощности :

где , .

Очевидно, что знак мощности зависит от знаков и . При согласованных направлениях (от одного узла) по знаку мощности можно судить о направлении передачи энергии.

Если , то элемент в данный момент времени потребляет энергию и является пассивным. Если , то элемент отдает мощность во внешнюю цепь, т.е. работает как источник и является активным.

Описание топологии цепи (соединений элементов) определяется законами Кирхгофа. Уравнения соединений (Кирхгофа) – это узловые и контурные уравнения топологии цепи.

Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю для любого момента времени (рис.1.2,а

Рис.1.2.Токи в узле цепи (а

) и напряжения в контуре (
б
)

Обычно токи, направленные к узлу, считаются положительными, а токи, направленные от узла, – отрицательными.

Алгебраическая сумма напряжений по замкнутому контуру (рис.1.2б

) равна нулю для любого момента времени . С положительными знаками принимаются слагаемые, соответствующие напряжениям, направления (полярности) которых совпадают с направлением обхода контура, а с отрицательными знаками – несовпадающие.

Например, для приведенных примеров:

(рис. 1.2а

(рис. 1.2б

Характер процессов в электрической цепи зависит от топологии цепи и от типа ее элементов.

Глава 2. Методы расчета простых резистивных цепей.

2.1. Резистивный элемент: определение и особенности.

Резистивный элемент – это идеализированный двухполюсный элемент, описывающий в количественном отношении только одну сторону реального процесса – необратимое преобразование электромагнитной энергии в другие виды (потери).

Резистивный элемент полностью определяется своей вольтамперной характеристикой (ВАХ). Для линейных резистивных элементов уравнения ВАХ описываются законом Ома.

На рис.1.3. приведено условное обозначение элемента, его ВАХ и временные зависимости тока и напряжения на элементе ,

иллюстрирующие основное свойство элемента.

Рис.1.3. Резистивный элемент: а

— обозначение линейного элемента и его ВАХ,
б
– временные зависимости
,
и для линейного резистора,
в
– нелинейный резистивный элемент и его ВАХ,
г
– варианты конструктивного исполнения резисторов

Уравнение элемента связывает ток ,

протекающий по элементу и напряжение на полюсах элемента.

Для резистивного элемента уравнения элемента и ВАХ совпадают:

где – сопротивление, – проводимость резистора, , , и параметры элемента .

Параметры и являются константами и имеют смысл только для линейных резисторов.

Функциональные уравнения ВАХ нелинейного резистора (уравнения элемента) можно записать в виде нелинейных зависимостей или .

Эти зависимости могут быть представлены в различных формах, например, графически, в виде таблицы либо приближенными аналитическими выражениями.

Мощность в линейном резисторе определяется выражением

Отсюда следует, что для любых значений . Следовательно, резистор потребляет электромагнитную энергию, т.е. он пассивен.

Выражения (1.7) и (1.8) позволяют сделать вывод о совпадении на линейном резисторе формы тока и формы напряжения с точностью до масштабных коэффициентов и .

Это важнейшее свойство линейного резистивного элемента широко используется в электротехнической практике: линейный резистор – весьма удобный датчик тока (преобразователь тока в напряжение).

Наиболее близким реальным прототипом к линейному резистивному элементу можно считать проволочное сопротивление.

Простыми резистивными цепями называют такие цепи, элементы которых (резисторы) соединены или только последовательно, или только параллельно, или только последовательно и параллельно.

Параллельное (последовательное) соединение нескольких однотипных элементов может быть заменено одним элементом. Поэтому простую цепь с одним источником путем объединения элементов, включенных только параллельно или только последовательно, можно свести к цепи, содержащей лишь один элемент. Резистивные цепи, которые указанным путем не могут быть к одному элементу активного резистора, называются сложными.

Расчет простых резистивных цепей с одним источником производится с использованием закона Ома. При наличии нескольких источников используется метод наложения.

2.2. Параллельные цепи

Пусть электрическая цепь содержит два резистора и источник тока:

Определим напряжение в цепи и токи в ветвях, если известны величины сопротивлений резисторов и ток источника. Учитывая заданное направление тока и выбранные направления токов и , составляем уравнение по ЗКТ:

, откуда .

Так как для токов и напряжения выбрана согласованная система отсчета, то

; .

Тогда

Следовательно, эквивалентное сопротивление двух параллельно соединенных резисторов определяется из соотношения:

и равно отношению произведения соединяемых резисторов к их сумме:

Напряжение цепи находится как произведение тока источника на эквивалентное сопротивление

Токи в ветвях вычисляются по закону Ома:

; .

Таким образом, выведено правило деления тока между двумя ветвями (или просто правило деления тока): ток в данной ветви пропорционален отношению сопротивления соседней ветви к сумме сопротивлений обеих ветвей.

Если использовать проводимости ветвей и , то правило деления тока можно записать так:

; .

Таким образом, ток в данной ветви пропорционален проводимости этой ветви к сумме проводимостей ветвей. Последнее соотношение можно объединить в одно:

где − эквивалентная проводимость цепи.

Аналогично можно доказать, что для параллельно соединенных резисторов:

2.3. Последовательные цепи

Последовательное соединение элементов

Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.

Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.

В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:

Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:

Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.

Проходящий по цепи ток везде одинаковый:

Прикладываемое напряжение является суммой напряжений на каждом резисторе:

Следовательно, рассчитать можно общее:

Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.

Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.

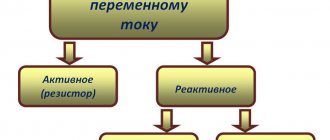
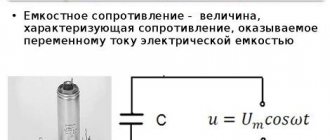
Участок цепи с ёмкостным элементом

Ёмкостным или С-элементом принято называть такой идеализированный элемент схемы замещения, который, в энергетическом отношении, способен лишь к преобразованию электрической энергии источника и её накоплению в виде энергии собственного электрического поля (поля зарядов). При определенных условиях он способен совершать обратное преобразование, отдавая всю накопленную энергию без остатка во внешнюю цепь (рис. 11).

Рис. 11.

Прообразом этого идеализированного -элемента является электротехническое устройство, называемое конденсатором и, наоборот,

С-элемент является идеализированной моделью конденсатора. Конденсаторы, кроме указанного свойства, обладают ещё рядом свойств, не являющихся для них основными, и поэтому эти свойства в модели не учитываются.

Из курса физики известно соотношение, связывающее величину заряда, накопленного конденсатором, с напряжением между его выводами

, (50)

где q

– заряд на одной из обкладок конденсатора (по абсолютной величине), измеряется в кулонах (Кл);
uc
– разность потенциалов между выводами конденсатора, измеряется в вольтах (В).

Параметр С

– количественно характеризует способность ёмкостного элемента запасать электрическую энергию, т. е. накапливать заряды. Этот параметр называется электрической ёмкостью и измеряется в фарадах (Ф).

Известно также, что электрический ток через конденсатор имеет другую физическую природу нежели ток проводимости. Однако количественно ток через конденсатор (ток через -элемент) можно определить как скорость изменения зарядов, сосредоточенных на его обкладках

. (51)

Подставив (50) в (51), получим, с учётом, что С

-элемент линейный:

. (52)

Соотношение (52), как и (40), показывают, что мгновенные значения напряжения и тока на L

-элементе, а также и на
С
-элементе не связаны законом Ома.

Согласно определению С

-элемент безвозвратно электрическую энергию не потребляет. Однако для него также как и для
L
-элемента можно ввести понятие о мгновенной мощности
р
. Под ней понимают скорость преобразования энергии, поступающей в -элемент, в энергию его собственного поля зарядов и наоборот:

отсюда получим

или

. (53)

Соотношение (53) определяет энергию собственного поля С-

элемента, накопленную к рассматриваемому моменту времени
t
1. Заметим, что (53) также наглядно определяет параметр
С
, как количественную характеристику
С
-элемента, показывающую его способность накапливать электрическую энергию: чем больше
С
, тем при прочих равных условиях больше
W
.

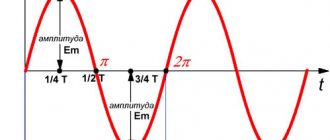
Пусть к цепи с С

-элементом приложено синусоидальное напряжение (рис. 11)

Согласно (52) определим ток, протекающий через этот элемент

. (54)

При синусоидальном напряжении ток ёмкостного элемента также синусоидален; напряжение и ток изменяются с одинаковой частотой; ток опережает напряжение по фазе на четверть периода ψi

= ψ
u
+ 90 º; угол сдвига фаз φ = ψ
u
– ψ
i
= – 90º.

Из (49) получим закон Ома для амплитудных

(55)

или действующих значений напряжения и тока

. (56)

Величина имеет размерность Ом, носит название ёмкостного сопротивления -элемента и обозначается

В этом случае (56) можно записать так

(57)

Определим запись закона Ома в комплексной форме. Для этого перейдем от и как синусоидальных функций времени к однозначно изображающим их комплексам действующих значений напряжения и тока

Возьмем формальное отношение

. (58)

Учитывая (56) и (19), получим окончательно

или . (59)

Это есть закон Ома в комплексах действующих значений напряжения и тока.

Величина jxс

называется комплексным сопротивлением ёмкостного элемента. Она
условно измеряется в Омах и является отрицательным мнимым числом, модуль которого равен xс
.

Векторная диаграмма, соответствующая соотношению (59) приведена на рис. 12. На ней показано, что вектор опережает вектор на 90º.

ψi
=ψ
u
+90º

Рис. 12.

Волновая диаграмма тока и напряжения на участке с С

-элементом приведена на рис. 13.

ψi

π/2

u
,
i

ωt

i
(
t
)

u
(
t
)

Рис. 13

Рассмотрим энергетические процессы, протекающие в цепи с С

-элементом. Мгновенная мощность на ёмкостном элементе

. (59)

График p(t)

приведён на рис.13. Видно, что мгновенная мощность в цепи с
С
-элементом колеблется с частотой 2ω и амплитудой
U I
вокруг нулевого положения. Следовательно, в этой цепи работа не совершается и энергия источника питания безвозвратно не потребляется. В тоже время происходит периодический обмен энергией между источником и элементом. Рассмотрим этот процесс.

В течение 1-ой четверти периода основной частоты (промежуток времени между точками 1 и 2 на рис.13) U

> 0 и
i
> 0 следовательно,
p
> 0 т. е.
С
-элемент работает в режиме потребления энергии. Потребляемая энергия запасается в электростатическом поле
С
-элемента. В течение 2-ой четверти периода (промежуток времени между точками (2 и 3)
u
> 0, а
i
< 0, т. е. и
С
-элемент работает в режиме источника. Происходит обратный процесс преобразования запасённой энергии
С
-элементом, которая отдаётся источнику питания. Далее процесс повторяется при отрицательном напряжении.

Интенсивность обмена энергией принято характеризовать наибольшим значением скорости преобразования энергии, т. е. амплитудным значением мгновенной мощности. Как следует из (59)

С учетом (57) получим

(60)

Эту величину называют реактивной мощностью С

-элемента. Единицей измерения этой мощности служит ВАр.

Рассмотренные модели элементарных участков цепи позволяют рассмотреть поведение более сложных участков электрических цепей. Простейшими являются модели участков с последовательным или параллельным соединением рассмотренных элементарных моделей.

6. Анализ участка схемы с последовательным соединением и — элементов

С помощью рассмотренных элементов можно изобразить линейную схему замещения любого электротехнического устройства. Например, катушку индуктивности на достаточно низкой частоте синусоидального тока можно представить следующей схемой замещения.

Рис. 14.

Допустим известно напряжение на зажимах катушки индуктивности

(Положим ψu

=0), а также сопротивление
R
к и индуктивность
L
к. Необходимо определить остальные параметры режима её работы. Согласно второго закона Кирхгофа для данной цепи можем записать уравнение для мгновенных значений напряжений:

(61)

или

. (62)

Из соотношения (62) видно, что для определения i

(
t
) необходимо решить дифференциальное уравнение. Анализ можно упростить, если перейти к символическому методу расчета такого участка схемы. В комплексной форме уравнение (61) будет иметь вид

. (63)

Согласно (33) и (47) это уравнение можно записать

. (64)

Поскольку элементы в схеме соединены последовательно, то через них протекает один и тот же ток. Тогда

. (65)

Уравнение (61) связывает общее напряжение, приложенное к этой цепи, с током, протекающим в ней. Т. е. (65) есть закон Ома для данной цепи в комплексной форме. Величина:

(66)

измеряется (условно) в Омах и называется полным комплексным сопротивлением участка этой цепи. Эту величину можно интерпретировать в виде векторов на комплексной плоскости.

Рис. 15.

Действительная часть комплексного сопротивления z

называется активным сопротивлением цепи. Мнимая её часть:

называется модулем комплексного сопротивления -элемента. Треугольник представленный z

и её составляющими на рис.15 носит название
треугольника сопротивлений. Соотношение (66) определяет алгебраическую форму представления комплекса z
. В расчетах получила распространение показательная форма представления
z
, (67)

где носит название модуля полного комплексного сопротивления или полного сопротивления участка цепи, измеряется в Омах; носит название аргумента комплекса или фазы полного комплексного сопротивления , измеряется в угловых градусах или в радианах. Для сторон треугольника (рис.15) справедливы соотношения

С учётом (63) можно определить вектор из (65):

(68)

> 0 для линейных элементов. Тогда φ > 0 и из (68) видно, что вектор тока в такой цепи отстаёт от вектора на угол 0<�φ<90º. Определив из (68) вектор , можно определить падение напряжения на каждом элементе, используя ранее установленные формулы закона Ома для этих элементов

; (69)

. (70)

Построим векторную диаграмму (рис. 16). Построение, как было сказано ранее, начинаем с выбора масштаба по току mi

(А/см) и напряжению
mu
(В/см). Определим вектор заданного напряжения. Его модуль , фаза ψ
u
= 0, т. е. вектор располагается вдоль оси действительных чисел (
+
1). Откладываем от т.0 в положительном направлении оси
+
1отрезок длиной
U/mu
(см) и его конец отмечаем стрелкой. Вектор построен.

+90º

Рис. 16.

Далее строим вектор тока . Этот вектор, как было установлено, отстаёт от вектора на угол φ. Причём 0<�φ<90º. Поэтому в IV четверти координатной плоскости проводим луч 0М под углом φ к оси +1. На этом луче от точки 0 откладываем отрезок (см). Его конец отмечаем стрелкой. Вектор построен. Строим вектор . Как было установлено ранее, ток через R

-элемент и падение напряжения на нём совпадают по фазе. Это подтверждают соотношения (68) и (69). Для векторной диаграммы это означает, что вектора совпадают по направлению. Поэтому на том же луче 0М от точки 0 откладываем отрезок, равный (см), его конец отмечаем стрелкой. Вектор построен. Наконец, строим вектор . Ранее было установлено, что падение напряжения на
L
-элементе опережает ток через этот элемент по фазе на 90º. Это подтверждают соотношения (68) и (70). Для векторной диаграммы данный ввод означает, что вектор должен быть перпендикулярен вектору и направлен в сторону оси
+
1 (поскольку разность фаз между и составляет +90º, а за положительное направление при повороте векторов в электротехнике принято направление против часовой стрелки). Из конца вектора (точка К на рис. 16) восстанавливаем перпендикуляр к лучу 0М в направлении оси
+
1. На перпендикуляре КN от точки К откладываем отрезок длиной, равной (см). Конец этого отрезка отмечаем стрелкой. Вектор построен. В случае верного построения всех векторов на данной диаграмме, конец вектора совпадает с концом вектора . Т. е. сумма векторов и равна вектору , что является геометрической интерпретацией 2-го закона Кирхгофа для данной цепи (63).

Рассмотренные вектора , , образуют прямоугольный треугольник, называемый треугольником напряжений. Для сторон этого треугольника справедливы соотношения:

. (71)

В заключение проанализируем энергетические процессы, протекающие в этой цепи. Как было установлено, интенсивность энергетических процессов, протекающих на участке цепи с R

-элементом, можно характеризовать активной мощностью:

, (72)

а интенсивность процессов, протекающих на участке цепи с L

-элементом – реактивной мощностью:

. (73)

Поскольку в данной цепи включён R

-элемент, то часть энергии источника питания будет безвозвратно потребляться на
R
-элементе. В то же время из-за наличия
L
-элемента в этой цепи будет происходить непрерывный обмен (с частотой 2ω) энергией (циркуляция энергии) между магнитным полем
L
-элемента и источником питания. Для характеристики общего энергетического режима цепи вводят понятие о полной мощности.

Определим её величину. Из (71) и (72) можно записать

(74)

(75)

Возведём в квадрат (70) и (71) и сложим полученные результаты

(76)

или

,(77)

где S

– полная мощность этого участка цепи, измеряемая в вольтамперах (ВА).

Можно записать соотношение между полной мощностью и её составляющими в комплексной форме. Для этого каждую сторону треугольника сопротивлений (рис. 15) умножим на . Вновь образованный прямоугольный треугольник (рис. 17) определяет своей гипотенузой полную мощность, а катетами – активную и реактивную мощности. Данный треугольник называется треугольником мощностей. Его стороны связаны соотношением:

. (78)

– полная комплексная мощность данного участка цепи. Её модуль

Рис. 17.

Полная мощность и её составляющие измеряются единицами мощности одинакового масштаба. Однако для того, чтобы подчеркнуть разную физическую природу энергетических процессов, интенсивность которых они оценивают, эти единицы измерения называют по-разному:

Треугольники сопротивлений (рис. 15), напряжений (рис. 16) и мощностей (рис.17) подобны. Из этого, в частности, следует, что

.(79)

Предоставляем студентам самостоятельно провести аналогичный анализ для участка цепи, содержащего последовательное соединение R

и C-элементов.

Параллельное соединение

Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.

Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:

общий ток: I = I1 + I2 + … + In;
общее напряжение: U = U1 = U2 = … = Un;
Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.

Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.

Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.

Расчёт при смешанном соединении устройств

Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.

Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.

Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.

Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.

Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.

Параллельное соединение элементов цепи при переменном напряжении

Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.

Параллельно соединение элементов цепи.

Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи

IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,

Um – амплитудное значение переменного тока.

Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже

Напряжение и токи при параллельном соединении.

Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения

где g – активная проводимость, b – реактивная проводимость.

Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.

Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы

Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.

Определим зависимость между напряжением и силой тока в параллельной цепи

где y – полная проводимость,

ψ – разность фаз между напряжением и током в цепи.

Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид

где Um – амплитудное значение переменного напряжения,

Im – амплитудное значение переменного тока,

y – полная проводимость цепи.

Физические формулы и примеры вычислений

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.

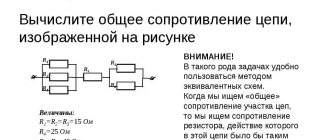
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:

R1 = 1 Ом;
R2 = 2 Ом;
R3 = 3 Ом;
R4 = 6 Ом;
R5 = 9 Ом;
R6 = 18 Ом;
R7 = 2Ом;
R8 = 2Ом;
R9 = 8 Ом;
R10 = 4 Ом.

Напряжение, поданное на схему:

Требуется рассчитать токи на всех резистивных элементах.

Для расчётов применяется закон Ома:

I = U/R, подставляя вместо R эквивалентное сопротивление.

Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.

Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.

На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:

АВ – участок, имеющий две параллельных ветви;
ВС – отрезок, вмещающий в себя последовательное сопряжение;
CD – отрезок схемы с расположением трёх параллельных цепочек.

Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:

Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.

Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:

Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.

В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:

Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.

Далее, используя закон Ома, находят ток в последнем последовательном участке:

I = U/ Rэкв. = 24/56,83 = 0,42 А.

Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:

UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.

Следующим шагом станет определение токов на параллельных отрезках AB и CD:

I1 = UAB/R1 = 0,35/1 = 0,35 А;
I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
I3 = UCD/R6 = 0,17/18 = 0,009 А;
I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
I7 = UCD/R10 = 0,17/4 = 0,04 А.

Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.

U9 = R9*I6 = 8*0,02 = 0,16 В.

Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.

U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.

После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:

I4 = U7,8/R7 = 1/2 = 0,5 A;
I5 = U7,8/R8 = 1/2 = 0,5 A.

Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.

Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.

. Электрическая цепь состоит из отдельных частей (объектов), выполняющих определенные функции и называемых
элементами цепи
. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устройства, производящие электрическую энергию, называются
генераторами
или
источниками электрической энергии
, а устройства, потребляющие ее –
приемниками
(потребителями) электрической энергии.

У каждого элемента цепи можно выделить определенное число зажимов (полюсов

), с помощью которых он соединяется с другими элементами. Различают
двух
–и
многополюсные
элементы. Двухполюсники имеют два зажима. К ним относятся источники энергии (за исключением управляемых и многофазных), резисторы, катушки индуктивности, конденсаторы. Многополюсные элементы – это, например, триоды, трансформаторы, усилители и т.д.

Все элементы электрической цепи условно можно разделить на активные

и
пассивные
. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются
линейными
, в противном случае они относятся к классу
нелинейных
. Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их как линейных, что существенно упрощает математическое описание и анализ процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются
параметрами
элемента.

Если параметры элемента не являются функциями пространственных координат, определяющих его геометрические размеры, то он называется элементом с сосредоточенными параметрами

. Если элемент описывается уравнениями, в которые входят пространственные переменные, то он относится к классу
элементов с распределенными параметрами
. Классическим примером последних является линия передачи электроэнергии (длинная линия).

Цепи, содержащие только линейные элементы, называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит ее к классу нелинейных.

Рассмотрим пассивные элементы цепи, их основные характеристики и параметры.

1. Резистивный элемент (резистор)

Условное графическое изображение резистора приведено на рис. 1,а. Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением r (Ом´ м) или обратной величиной – удельной проводимостью (См/м).

В простейшем случае проводника длиной и сечением S его сопротивление определяется выражением

В общем случае определение сопротивления связано с расчетом поля в проводящей среде, разделяющей два электрода.

Основной характеристикой резистивного элемента является зависимость (или ), называемая вольт-амперной характеристикой (ВАХ). Если зависимость представляет собой прямую линию, проходящую через начало координат (см.рис. 1,б), то резистор называется линейным и описывается соотношением

или

где — проводимость. При этом R=const.

Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое и дифференциальное сопротивления.

2. Индуктивный элемент (катушка индуктивности)

Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.

Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,

В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков , где .

Основной характеристикой катушки индуктивности является зависимость , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом

Нелинейные свойства катушки индуктивности (см. кривую на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической и дифференциальной индуктивностями.

3. Емкостный элемент (конденсатор)

Условное графическое изображение конденсатора приведено на рис. 3,а.

Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними

и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними. Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная диэлектрическая проницаемость =const. В этом случае зависимость представляет собой прямую линию, проходящую через начало координат, (см. рис. 3,б) и

У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость является функцией напряженности поля, что обусловливает нелинейность зависимости (рис. 3,б). В этом случае без учета явления электрического гистерезиса нелинейный конденсатор характеризуется статической и дифференциальной емкостями.

Схемы замещения источников электрической энергии

Свойства источника электрической энергии описываются ВАХ , называемой внешней характеристикой источника.

Далее в этом разделе для упрощения анализа и математического описания будут рассматриваться источники постоянного напряжения (тока). Однако все полученные при этом закономерности, понятия и эквивалентные схемы в полной мере распространяются на источники переменного тока. ВАХ источника может быть определена экспериментально на основе схемы, представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах 1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого может изменяться с помощью переменного нагрузочного резистора (реостата) RН.

В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она имеет две характерные точки, которые соответствуют:

а – режиму холостого хода

;

б – режиму короткого замыкания

Для большинства источников режим короткого замыкания (иногда холостого хода) является недопустимым. Токи и напряжения источника обычно могут изменяться в определенных пределах, ограниченных сверху значениями, соответствующими номинальному режиму

(режиму, при котором изготовитель гарантирует наилучшие условия его эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами изменения напряжения и тока. Следует отметить, что многие источники (гальванические элементы, аккумуляторы) имеют линейные ВАХ.

Прямая 2 на рис. 4,б описывается линейным уравнением

(1)

где — напряжение на зажимах источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а); — внутреннее сопротивление источника

Уравнение (1) позволяет составить последовательную схему замещения

источника (см. рис. 5,а). На этой схеме символом Е обозначен элемент, называемый
идеальным источником ЭДС
. Напряжение на зажимах этого элемента не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б. На основании (1) у такого источника . Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.

Если ВАХ источника линейна, то для определения параметров его схемы замещения

необходимо провести замеры напряжения и тока для двух любых режимов его работы.

Существует также параллельная схема замещения источника. Для ее описания разделим левую и правую части соотношения (1) на . В результате получим

или

(2)

где ; — внутренняя проводимость источника

Уравнению (2) соответствует схема замещения источника на рис. 6,а.

На этой схеме символом J обозначен элемент, называемый идеальным источником тока

. Ток в ветви с этим элементом равен и не зависит от напряжения на зажимах источника, следовательно, ему соответствует ВАХ на рис. 6,б. На этом основании с учетом (2) у такого источника , т.е. его внутреннее сопротивление .

Отметим, что в расчетном плане при выполнении условия последовательная и параллельная схемы замещения источника являются эквивалентными. Однако в энергетическом отношении они различны, поскольку в режиме холостого хода для последовательной схемы замещения мощность равна нулю, а для параллельной – нет.

Кроме отмеченных режимов функционирования источника, на практике важное значение имеет согласованный режим

работы, при котором нагрузкой RН от источника потребляется максимальная мощность

(3)

Условие такого режима

(4)

В заключение отметим, что в соответствии с ВАХ на рис. 5,б и 6,б идеальные источники ЭДС и тока являются источниками бесконечно большой мощности.

Литература

Основы
теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А
. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические
основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия, 1972. –240 с.
Каплянский А.Е.
и др. Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. –448 с.

Контрольные вопросы и задачи

Может ли внешняя характеристик источника проходить через начало координат?
Какой режим (холостой ход или короткое замыкание) является аварийным для источника тока?
В чем заключаются эквивалентность и различие последовательной и параллельной схем замещения источника?
Определить индуктивность L и энергию магнитного поля WМкатушки, если при токе в ней I=20А потокосцепление y =2 Вб.
Ответ: L=0,1 Гн; WМ=40 Дж.
Определить емкость С и энергию электрического поля WЭконденсатора, если при напряжении на его обкладках U=400 В заряд конденсатора q=0,2´ 10-3 Кл.
Ответ: С=0,5 мкФ; WЭ=0,04 Дж.
У генератора постоянного тока при токе в нагрузке I1=50Анапряжение на зажимах U1=210 В,а притоке, равном I2=100А, оно снижается до U2=190 В.
Определить параметры последовательной схемы замещения источника и ток короткого замыкания.
Ответ:
Вывести соотношения (3) и (4) и определить максимальную мощность, отдаваемую нагрузке, по условиям предыдущей задачи.
Ответ: