Емкостное сопротивление: что это такое, формула, пример расчета

При проектировании электрический цепей, оборудования и электроприборов учитываются многие свойства проводников. Одним из важных свойств считается емкостное сопротивление.

В данной статье будет подробно описано — что такое емкостное сопротивление конденсатора. Так же будет приведена формула расчета такого параметра, описана работа конденсатора в цепи переменного тока и сферы применения ёмкостного сопротивления.

Определение

Сопротивлением называют физический эффект противодействия протеканию тока по любой электрической цепи. Этим свойством обладают все проводники электрического тока. Данная величина измеряется в Ом.

Емкостное электрическое сопротивление является величиной, благодаря которой можно понять, что в цепи присутствует конденсатор. Емкостные сопротивления конденсатора рассчитываются только для цепей переменного тока, без учета наличия в них резисторов.

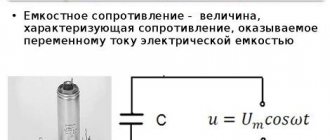
Конденсатор обозначается на схеме буквой «С», а его ёмкостное сопротивление «Xc».

Видео

Кофе капсульный Nescafe Dolce Gusto Капучино, 3 упаковки по 16 капсул

1305 ₽ Подробнее

Кофе в капсулах Nescafe Dolce Gusto Cappuccino, 8 порций (16 капсул)

435 ₽ Подробнее

Лучшие игровые клавиатуры

Принцип работы

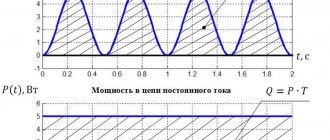
Конденсатор с определенной ёмкостью работает по принципу периода, который состоит из заряда и разряда элемента. Период делится на 4 части:

Первая часть предполагает рост напряжения. В этот момент сопротивление конденсатора минимально, а зарядный ток очень высокий.
Во второй четверти происходит наполнение его ёмкости за счет зарядного тока.
В третьей четверти конденсатор полностью заряжается, при этом происходит снижение тока вплоть до 0. ЭДС возрастает с эффектом смены своей направленности.
В последней четверти происходит разряд элемента. На этом этапе ЭДС будет в пределах 0, а ток постепенно нарастать.

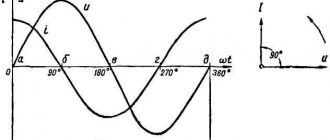
Все описанные процессы за один период определяют дальнейший фазный сдвиг на 90 градусов.

Природа возникновения емкостного сопротивления полностью зависит от нескольких факторов:

Обязательно наличие конденсатора в цепи.
По цепи должен течь только переменный ток.
Сопротивление проводника должно быть меньше емкости конденсатора.

Все эти факторы помогают рассчитать наиболее правильное значение ёмкостных характеристик для наиболее эффективной работы электроцепи.

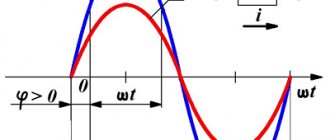
Фазор

Благодаря фазовым векторам сложный и меняющийся во времени сигнал можно представить в виде комплексного числа (не зависит от времени) и сложного сигнала (зависит от времени). Фазоры делятся на основе А (амплитуды), v (частоты) и θ (фазы). Это приносит большую пользу, ведь частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В подобных ситуациях факторы исключают факультативную характеристику и основываются лишь на A и θ.

К примеру, можно представить A⋅cos (2πνt + θ) просто как комплексную постоянную Aeiθ. Из-за того, что фазовые векторы передаются величиной и углом, наглядно изображаются вектором в плоскости x-y.

Фазор можно рассматривать с позиции вектора, вращающегося вокруг начала координат. Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0

Расчет

Расчет электрического емкостного сопротивления цепи делается по формуле. Она состоит из следующих значений:

«Xc» — является емкостным сопротивлением в Омах.
«1» — период полного заряда и разряда элемента.
«w» — круговая частота переменного тока с емкостью, рад/сек.
«C» — емкость конденсатора, единицы измерения Фарад.

Сама формула при этом выглядит следующим образом:

При помощи этой формулы легко рассчитывается Xc. Для этого требуется просто умножить циклическую частоту переменного тока на известную величину емкости конденсатора. Далее необходимо будет один период разделить на полученное значение. Таким образом можно всегда найти сопротивление конденсатора в Ом.

Рассчитываться емкостное сопротивление может так же с помощью и другой формулы, которая приведена на рисунке ниже.

При расчетах по данной формуле прослеживаются следующие зависимости:

Емкость конденсатора и частота тока всегда выше сопротивления.
От величин емкости и частоты зависит скорость одного периода заряда/разряда конденсатора.

Также стоит учесть, что после подключения конденсатора в цепь постоянного тока, его сопротивление сильно увеличивается. Объясняется причина такого явления довольно просто — отсутствует частота протекания электричества.

Реактивное сопротивление катушки индуктивности

Из опыта выше мы можем сделать вывод, что сопротивление катушки зависит от частоты и вычисляется по формуле

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

F — частота, Гц

L — индуктивность

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

где

ХL — реактивное сопротивление катушки, Ом

П — постоянная и равна приблизительно 3,14

Подробнее здесь: https://www.ruselectronic.com/news/katushka-induktivnosti-v-tsepi-postoyannogo-i-peremennogo-toka/

П — постоянная и приблизительно равна 3,14

F — частота, Гц

L — индуктивность, Генри

Характеристики элемента

Для того чтобы понять, что такое емкостное сопротивление, необходимо разобраться с его основной характеристикой, которая называется емкостью. Емкостью называется накопительная способность элемента. Она заключается в накоплении определенной доли электрического тока за определённый промежуток времени. Единицей измерения этой величины является Фарад (Ф или F).

Элемент заряжается электричеством до определенного момента, после которого он начинает разряжаться и отдавать ток дальше по электроцепи. Время полного разряда напрямую зависит от величины сопротивления цепи. Чем выше это значение, тем меньше времени тратится на разрядку элемента. Для расчета ёмкостной характеристики используется следующее выражение:

Так же конденсаторы обладают рядом дополнительных характеристик. К ним относят:

Общую удельную емкость. Является отношением массы диэлектрических пластин и емкостных параметров.
Напряжение. Параметр определяется как рабочее напряжение, которое способен выдержать элемент.
Температурная стойкость или стабильность. Это температурный параметр, который не влияет на изменение емкости.
Изоляционное сопротивление. Является величиной точки утечки и саморазряда.
Эквивалентная нагрузка. Значение, определяющее потери на выводе или контактах устройства.
Абсорбция. Разность потенциалов в момент разряда до 0.
Полярность. Параметр свойственен элементам, которые работают строго при подаче на обкладку потенциала определенного значения (плюс или минус).
Индуктивность. Свойство конденсатора образовывать на контактах индуктивное сопротивление. Такое свойство может наделить элемента параметрами колебательного контура.

Все эти значения строго учитываются при проектировании цепей или схем электрического оборудования.

О заряде конденсатора.

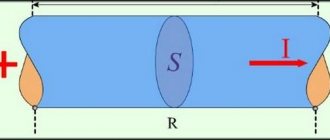
Замкнем цепь. В цепи пойдет ток заряда конденсатора. Это значит что с левой обкладки конденсатора часть электронов уйдет в провод, а из провода на правую обкладку зайдет такое же количество электронов. Обе обкладки будут заряжены разноименными зарядами одинаковой величины.

Между обкладками в диэлектрике будет электрическое поле.

А теперь разомкнем цепь. Конденсатор останется заряженным. Закоротим куском провода его обкладки. Конденсатор мгновенно разрядится. Это значит что с правой обкладки уйдет в провод избыток электронов, а из провода на левую обкладку войдет недостаток электронов. На обоих обкладках электронов будет одинаково, конденсатор разрядится.

До какого напряжения заряжается конденсатор?

Импеданс

Кроме емкостного, конденсатор еще имеет общее сопротивление или импеданс. Данное значение определяется с учетом значений трех параметров: индуктивного, резистивного и емкостного сопротивления.

Для вычисления импеданса применяется следующая формула:

В данном выражении используются следующие сопротивления:

xL — индуктивное;
xC — емкостное;
R — активное.

Активное сопротивление цепи появляется вследствие возникновения в ней ЭДС. Так как переменный ток по своей природе импульсный, то электромагнитный поток может довольно незначительно изменяться, а это приводит к сдвигу постоянного значения ЭДС.

Емкостные и индуктивные величины взаимосвязаны. По разнице между ними легко находят реактивную составляющую цепи.

Отсюда легко проследить, от чего зависит само реактивное сопротивление:

Если реактивная величина больше 0, то устройство больше нагружено индуктивным значением.
Если реактивное значение равно 0, то емкость не нагружается активным сопротивлением.
Если реактивность меньше 0, то элемент имеет высокое емкостное сопротивление.

Активное сопротивление считается невосполнимой величиной. Она тратится на преобразование тока в иной вид энергии. Реактивная величина неизменна для актуальной цепи переменного тока.

Активное сопротивление

И начнем мы статью не с реактивного сопротивления, как ни странно, а с простого и всеми нами любимого радиоэлемента — резистора, который, как говорят, обладает активным сопротивлением. Еще иногда его называют омическим. Как нам говорит вики-словарь, «активный — это деятельный, энергичный, проявляющий инициативу». Активист готов всегда рвать и метать даже ночью. Он готов ПОЛНОСТЬЮ выложиться и потратить всю энергию во благо общества.

То же самое можно сказать и про другие нагрузки, обладающие активным сопротивлением. Это могут быть различные нагревательные элементы, типа тэнов, а также лампы накаливания.

Расчет

Узнав, по какой формуле делаются необходимые вычисления и поняв смысл емкостного сопротивления, можно заняться расчетом данной величины.

Например, сделаем расчет на основе следующих данных:

Емкость конденсатора C=1мкФ;
В цепи также имеется активное сопротивление R, которое равно 5 кОм;
Индуктивное сопротивление цепи xL составляет 4.5 кОм;
Частота переменного тока равна 50 Гц;
Напряжение 50 вольт.

На основе этих данных необходимо будет найти сопротивление конденсатора.

Емкостное сопротивление определим следующим образом:

xC=1/(2πfC)=1/(2×3.14×50×1×10-6)=3184 Ом или округленно 3.2 кОм.

Для определения величины тока в этой цепи воспользуемся законом Ома:

I=U/xC=50/3184=0.0157 ампер или 15.7мА.

После этого определяются параметры общего сопротивления:

Z=(R²+(xL-xC)²)½=(5000²+(4500–3184)²)½=5170 Ом или 5.1 кОм.

По данным расчётам можно определить влияние емкостного элемента на электроцепь. Главное понимать, какие физические величины используются в данных формулах для выполнения правильных вычислений.

О заряде конденсатора.

Между обкладками в диэлектрике будет электрическое поле.

До какого напряжения заряжается конденсатор?

Применение

В электронных цепях очень часто конденсатор используется в качестве фильтрующего элемента. При этом инженеры учитывают способ подключения данного элемента:

При параллельном соединении конденсатора с цепью, устройство способно задерживать ток высокой частоты. Такой фильтр работает по принципу зависимости сопротивления от частоты тока. Чем выше частота, тем ниже будет сопротивление.
При последовательном включении фильтр уже отсеивает низкочастотные импульсы. Вторым свойством такого фильтра является возможность не пропускать постоянный ток.

Также большая доля использования таких устройств приходится на звуковые усилители. Конденсатор способен отделить переменный и постоянный ток, а значит работать в качестве усилителя низкой частоты. При этом подбираются элементы с наименьшей емкостью.

Так же устройства используются для блоков питания постоянного тока или стабилизаторов. Тут применяется свойство разделения постоянной и переменной составляющей. Например, разделение ее между потребителями с помощью отдельных выходов для постоянного и переменного тока. В таких устройствах конденсатор разряжается, если нагрузка на цепь увеличивается за счет подключения нового устройства. Тем самым общая пульсация в цепи сглаживается. При необходимости можно передать ток обоих значений по одному проводнику. Делается это следующим образом — контакты с постоянным напряжением подключают к выводу емкости для прямого контакта с переменным напряжением. Таким образом происходит фильтрация частоты, сглаживание импульсов и передача постоянного тока потребителю. Такая схема используется в антенных усилителях, которые подключаются к телевизорам.

О реальном конденсаторе

Реальный конденсатор имеет одновременно два сопротивления: активное и емкостное. Их следует считать включенными последовательно.

Напряжение приложенное генератором к активному сопротивлению и ток идущий по активному сопротивлению совпадают по фазе.

Напряжение приложенное генератором к емкостному сопротивлению и ток идущий по емкостному сопротивлению сдвинуты по фазе на 90 . Результирующее напряжение приложенное генератором к конденсатору можно определить по правилу параллелограмма.

На активном сопротивлении напряжение Uакт и ток I совпадают по фазе. На емкостном сопротивлении напряжение Uc отстает от тока I на 90 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 .

Измерение и проверка

Измерить целостность конденсатора и его сопротивление можно при помощи мультиметра. Перед этим элемент обязательно необходимо отсоединить от цепи.

Проверка

Диагностика целостности конденсатора начинается с визуально осмотра его состояния. Любые трещины, вздутия или деформации корпуса можно считать неисправностью элемента. Если визуальный осмотр не дал никаких результатов, то элемент проверяется на пробой при помощи тестера.

Делается такая проверка следующим образом:

Элемент необходимо выпаять из схемы, а его контактные выводы замкнуть металлическим предметом для разрядки.
Мультиметр перемести в режим замера сопротивления.
Измерительные щупы соединить с контактами устройства.
Сопротивление исправного элемента будет измеряться бесконечным значением, которое будет превышать значение сопротивления утечки. Величина этой утечки при этом составляет 2 кОм.

Если показания меньше этого значения, значит элемент неисправен и пробит.

Замер

Замерить сопротивление можно так же с помощью мультиметра. Его надо будет перевести в режим измерения сопротивлений более 100 кОм. Далее необходимо соединить щупы прибора с контактами устройства. Некоторое время потребуется на полную зарядку элемента. После этого он покажет конечный результат, который не должен быть выше 100 кОм. Если этот порог преодолен, то можно сделать однозначный вывод о неисправности элемента.

Измерение емкости

Для замера емкости потребуется тестер с режимом СX. Если такого режима нет, проверить элемент будет невозможно. Далее требуется:

Полностью разрядить конденсатор.
На мультиметре выбирается режим СX.
Измерительные щупы соединить с контактными выводами устройства, строго соблюдая полярность.
Прибор должен показать величину больше 1, но при этом ее значение должно быть в пределах тех значений, которые указаны на корпусе детали. Если значение равняется 0 или находится за пределами указанных значений, то конденсатор можно признать неисправным.

Полученные мультиметром данные также можно считать ёмкостным значением, так как в момент проверки элемент проходит зарядку током.

Векторная диаграмма токов в цепи с конденсатором

Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению

I = IG + IC

Действующие величины составляющих тока:

IG = GU (13.31)

IC = BCU (13.32)

Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φa =0). Вектор IG совпадает по направлению с вектором U, а вектор IC направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC :

При напряжении u = Umsinωt соответствии с векторной диаграммой уравнение тока

i = Imsin(ωt + φ)

Соединение конденсаторов

Часто самого по себе конденсатора недостаточно. Поэтому такие электронные компоненты приходится объединять в группы, так называемые батареи. При таком подключении множество ёмкостей соединяются друг с другом для получения новой, обладающей другими характеристиками.

Выделяют 2 основных способа соединения деталей:

последовательный;
параллельный.

Последовательное соединение ёмкостей

При этом виде соединения множество деталей выстраивается в длинную цепь (от двух штук и более). Чаще всего на практике применяются комбинации из 2-5 деталей. Каждая предшествующая соединяется с последующей. В результате получается длинная цепочка, напоминающая вагоны в железнодорожном составе.

Последовательное включение

Последовательное соединение конденсаторов снижает их общую ёмкость. Вызвано это тем, что увеличивается толщина диэлектрика между обкладками прибора, а площадь их пересечения при этом остаётся неизменной (см. формулу выше). Как рассчитать суммарную ёмкость конденсатора при последовательном подключении, можно узнать из формулы ниже.

Ёмкость последовательно включенных конденсаторов

На деле такое подключение используется для получения нового значения ёмкости, но такой конденсатор просто не выпускается промышленностью. Например, имея два элемента номиналом 10 uF каждый и соединив их последовательно, можно получить общую ёмкость в 5 uF.

Пример последовательного расчёта

Другая особенность последовательного соединения – это увеличение общего напряжения. Если взять 2 ёмкости на 200 В каждую и подключить их описываемым способом, то итоговое напряжение батареи составит 200 + 200 = 400 вольт.