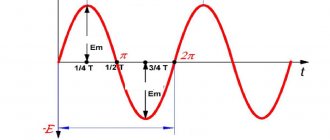
Для нахождения индукции магнитного поля в центре кругового проводника с током необходимо разбить этот проводник на элементы , для каждого из них найти вектор , а затем все эти векторы сложить. Так как все векторы направлены вдоль нормали к плоскости витка (рис. 11), то сложение векторов можно заменить сложением их модулей dB.
По закону Био-Савара-Лапласа модуль вектора :
.
Так как все элементы проводника перпендикулярны соответствующим радиусам-векторам , то sina = 1 для всех элементов . Расстояния r = R для всех элементов проводника . Тогда выражение для модуля вектора :
.
Теперь можно перейти к интегрированию:
.
Итак, индукция магнитного поля в центре кругового проводника с током:
(R – радиус витка с током I).
Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока
Закон Био-Савара–Лапласа описывает порождение магнитного поля током $I$ на элементе проводника длиной $dl$ в некоторой точке пространства ($\mu$ — магнитная проницаемость вещества в котором локализовано поле):
$d\vec{B}=\frac{\mu_{0}\mu }{4\pi }\frac{I\left[ d\vec{l}\vec{r}\right]}{r^{3}}\left( 1 \right)$
где $d \vec l ⃗$ — вектор, длина которого равна длине элемента проводника $dl$, направленный по току; $\vec r$ – радиус-вектор, который проведен от элемента $dl$ в точку, в которой исследуется магнитное поле. Поскольку в правой части формулы (1) находится векторное произведение, очевидно, что индукция элементарного магнитного поля будет направлена перпендикулярно плоскости, в которой находятся векторы $\vec r$ и $\vec l$ и при этом является касательной к силовой линии поля.
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Величину вектора $\vec{dB}$ из выражения (1) найдем как:
$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl\sin \alpha }{r^{2}}\left( 2 \right)$.
где $ \alpha $– угол между векторами $\vec r$ и $\vec l$ .
Конкретное направление $\vec{dB}$ находят по правилу буравчика (правилу правой руки):
Если правый винт вращать так, что его поступательное движение будет совпадать с направлением течения тока в избранном элементе, то вращение его головки укажет направление $\vec{dB}$.
Магнитные поля подчиняются принципу суперпозиции:
Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:
$\vec{B}=\sum\limits_{i=1}^N \vec{B}_{i} \left( 3 \right). $
Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:
$\vec{B}=\int {d\vec{B}_{i}} \left( 4 \right).$
Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:
Готовые работы на аналогичную тему
Курсовая работа Магнитное поле кругового тока 450 ₽ Реферат Магнитное поле кругового тока 220 ₽ Контрольная работа Магнитное поле кругового тока 250 ₽
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
- Выделить на проводнике с током элементарный отрезок $dl$.
- Записать для исследуемой точки поля закон Био – Савара – Лапласа.
- Определить направление элементарного поля $\vec{dB}$ в избранной точке.
- Воспользоваться принципом суперпозиции для магнитных полей (учесть, что суммируются векторы).
Магнитный поток. Теорема Гаусса для магнитного поля
Поток вектора магнитной индукции (или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S.
Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 14), то поток ФB вектора индукции через данную площадку S :
.
Рис. 14 Рис. 15
Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB вектора индукции через данную площадку S :
,
где α – угол между векторами и нормали к площадке S.
,Для того, чтобы найти поток ФB вектора магнитной индукции через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 16)иопределить элементарный поток вектора через каждую площадку dS по формуле:
где α – угол между векторами и нормали к данной площадке dS;
Тогда поток вектора через произвольную поверхность S равен алгебраической сумме элементарных потоков через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
– вектор, равный по величине площади площадки dS и направленный по вектору нормали к данной площадке dS .
.
Теорема Гаусса для магнитного поля
Для произвольной замкнутой поверхности S (рис. 17) поток вектора индукции магнитного поля через эту поверхность S можно рассчитать по формуле:
.
С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 17). Поэтому, с учетом того, что поток вектора индукции магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора через произвольную замкнутую поверхность S равен нулю, т.е.:
,
что составляет формулировку теоремы Гаусса для магнитного поля.
Магнитное поле кругового тока в его центре
Рисунок 1. Магнитное поле кругового тока в его центре. Автор24 — интернет-биржа студенческих работ
Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.
Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:
$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl_{1}\sin \alpha }{r^{2}}\left( 5\right).$
Из рис.1 мы видим:
- что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
- элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $\vec r$.
Учитывая сказанное выражение (5) представим в виде:
$dB=\frac{\mu_{0}\mu }{4\pi }\frac{Idl_{1}}{R^{2}}\left( 6 \right)$.
Обезличивая витки с током, положим далее $dl_1=dl$.
Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:
$B=\oint\limits_L {dB=} \frac{\mu_{0}\mu }{4\pi}\frac{I}{R^{2}}\oint\limits_L {dl} =\frac{\mu_{0}\mu }{4\pi}\frac{I}{R^{2}}2\pi R\to$
$B=\mu_{0}\mu \frac{I}{2R}\left( 7 \right)$.
Замечание 1
$L=2πR$ — длина окружности витка.
Индукция магнитного поля кругового тока на его оси
Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка — $R$ (рис.2).
Рисунок 2. Индукция магнитного поля кругового тока на его оси. Автор24 — интернет-биржа студенческих работ
Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:
- $\vec{r}=\vec{R}+\vec{h}$,
- $d\vec{l}\times \vec{r}=d\vec{l}\times \vec{R}+d\vec{l}\times \vec{h}(9).$
Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:
$\vec{B}=\oint\limits_L {dB=}$$\frac{\mu \mu_{0}}{4\pi }I\oint\limits_L \frac{d\vec{l}\times\vec{r}}{r^{3}} $ $=\frac{\mu \mu_{0}}{4\pi }\frac{I}{r^{3}}\left( \oint\limits_L{d\vec{l}\times \vec{R}+} \oint\limits_L {d\vec{l}\times \vec{h}}\right)\left( 10 \right).$
В выражении (10) при записи интеграла, мы учли, что величина вектора $\vec{r}$ не изменяется. Кроме этого вектор $\vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:
$\oint\limits_L {d\vec{l}\times \vec{h}} =(\oint\limits_L {d\vec{l})\times\vec{h}} =0\, \left( 11 \right),$
так как ( $\oint\limits_L {d\vec{l})=0.}$
Вычислим интеграл: $\oint\limits_L {d\vec{l}\times \vec{R}.}$ Введем единичный вектор ($\vec n$), нормальный к плоскости витка с током.
$\oint\limits_L {d\vec{l}\times \vec{R}=\oint\limits_L {\vec{n}Rdl=\vec{n}R}} \oint\limits_L {dl=\vec{n}R} 2\pi R=2\pi R^{2}\vec{n}\left( 12 \right)$.
Подставляем результаты интегрирования из (12) в (10), имеем:
$\vec{B}=\frac{\mu \mu_{0}}{4\pi }\frac{I}{r^{3}}2\pi R^{2}\vec{n}=\frac{\mu\mu_{0}I}{2}\frac{R^{2}}{\left( R^{2}+h^{2}\right)^{\frac{3}{2}}}\vec{n}\left( 13 \right)$
где при записи окончательного результата мы учли, что:
$r^{3}=\left( R^{2}+h^{2} \right)^{\frac{3}{2}}$.
§20. Электромагнитные силы, создаваемые магнитным полем
Проводник с током в магнитном поле. Энергия, заключенная в магнитном поле, может проявлять себя в виде электромагнитных сил, которые возникают при взаимодействии магнитного поля с движущимися электрическими зарядами. Электромагнитная сила, возникающая при движении электрического заряда в магнитном поле, действует на него в направлении, перпендикулярном движению и направлению силовых линий, и стремится вытолкнуть заряд за пределы поля (см. рис. 34).
Если поместить в магнитное поле проводник с током I, то между электронами, проходящими по проводнику, и магнитным полем возникнут электромагнитные силы, которые, складываясь, образуют результирующую силу F, стремящуюся вытолкнуть проводник из магнитного поля (рис. 48). Электромагнитная сила определяется законом Ампера. Он формулируется следующим образом. Электромагнитная сила, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поля В и длины проводника l:
F = IBl (48)
Если проводник расположен под углом ? к силовым магнитным
F = BIlsin? (48′)
Чтобы получить F в ньютонах, надо В брать в теслах, I — в амперax и l — в метрах.
Направление действия силы F обычно определяют по правилу левой руки: ладонь левой руки нужно расположить так, чтобы магнитные линии входили в нее и четыре вытянутых пальца совместить с направлением тока, тогда расположенный под прямым углом большой палец укажет направление действия электромагнитной силы. Сила F возникает только в том случае, если проводник расположен перпендикулярно или под некоторым углом к магнитным силовым линиям поля. Если же проводник расположен вдоль силовых линий поля, то электромагнитная сила будет равна нулю.
Для того чтобы изменить направление электромагнитной силы, как следует из правила левой руки, необходимо изменить направление тока в проводнике или же направление магнитного поля.
Возникновение электромагнитной силы F при взаимодействии проводника с током и магнитного поля можно наглядно представить как результат взаимодействия двух магнитных полей. Как известно, вокруг проводника с током возникает свое собственное круговое магнитное поле (рис. 49), которое будет складываться с внешним магнитным полем (например, постоянного магнита), в которое помещен проводник с током. При этом справа от проводника, где силовые линии поля проводника совпадают с линиями внешнего поля, происходит сгущение силовых линий; слева от проводника, где силовые линии поля проводника направлены навстречу линиям внешнего поля, происходит разрежение силовых линий. Магнитные силовые линии обладают свойством упругости, напоминающим свойство резиновых нитей. Стремясь сократиться по длине, они будут выталкивать проводник из области сгущения силовых линий в сторону их разрежения, т. е. справа налево. В результате возникает электромагнитная сила F.
Рис. 48. Электромагнитная сила, действующая в магнитном поле на проводник с током
Рис. 49. Сгущение и разрежение магнитных силовых линий при наличии в магнитном поле проводника с током.
Рис. 50.Электромагнитные силы,действующие в магнитном поле на виток или катушку с током.
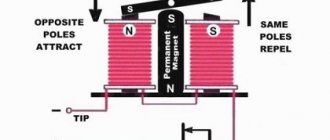
Виток с током в магнитном поле. Если поместить в магнитное поле не проводник, а виток (или катушку) с током и расположить его вертикально (рис. 50, а), то, применяя правило левой руки к верхней и нижней сторонам витка, получим, что электромагнитные силы F, действующие на них, будут направлены в разные стороны. В результате действия этих двух сил возникает электромагнитный вращающий момент М, который вызовет поворот витка, в данном случае по часовой стрелке. Этот момент
M = FD (49)
где D — расстояние между сторонами витка. Виток будет поворачиваться в магнитном поле до тех пор, пока он не займет положение, перпендикулярное магнитным силовым линиям поля (рис. 50, б). При таком положении через виток будет проходить наибольший магнитный поток. Следовательно, виток или катушка с током, внесенные во внешнее магнитное поле, всегда стремятся занять такое положение, чтобы через виток проходил возможно больший магнитный поток. Свойство витка и катушки с током поворачиваться в магнитном поле широко используется в электротехнике; электрические двигатели и ряд электроизмерительных приборов работают по этому принципу.
Для увеличения вращающего момента в электрических двигателях применяют не один виток, а несколько. Эти витки, соединенные соответствующим образом, образуют обмотку якоря электродвигателя.
Магнитное напряжение.
По аналогии с электрическим напряжением при расчете магнитных полей пользуются понятием магнитного напряжения Uм. Магнитное напряжение между двумя точками a и b однородного магнитного поля, расположенными на одной магнитной линии (рис. 2,а), выражается произведением напряженности поля и расстояния между этими точками:В более общем случае, если в однородном поле две точки а и b находятся на расстоянии L не на одной магнитной линии (рис. 2,б), сначала вычисляется напряженность H, затем продольная слагающая вектора напряженности вдоль отрезка ab, т. е. HL = H cosa, где a—угол между векторами Н и HL. Магнитное напряжениеВ неоднородном магнитном поле магнитное напряжение между двумя точками a и b равно сумме элементарных напряжении HLdL на элементарных участках dL вдоль выбранного пути между этими точками (рис. 2,в):
Магнитное напряжение Uм может зависеть от выбранного пути между начальной и конечной точками. Магнитное напряжение в системе СИ измеряется в амперах:
Магнитное напряжение вдоль произвольного замкнутого пути (контура) представляет собой МДС вдоль этого контура. Таким образом, МДС можно определить как сумму элементарных магнитных напряжении HLdL вдоль, замкнутого контура: где знак обозначает суммирование (интегрирование) по замкнутому контуру элементарных напряжений HLdL.