Активное реактивное и полное сопротивление. Треугольники сопротивлений

При прохождении тока в электрической цепи он подвергается противодействию ее отдельных частей, которое в электротехнике называется сопротивлением. Это приводит к потере части мощности. Чтобы правильно рассчитать параметры электрической цепи, нужно учитывать природу сопротивления и знать, в чем заключается действие различных его видов.

Что такое сопротивление

Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.

Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.

Индуктивное сопротивление

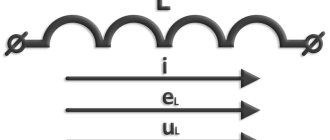
При увеличении силы тока порождается магнитное поле, обладающее различными характеристиками. Наиболее важной из них является индуктивность. Магнитное поле, в свою очередь, воздействует на проводник, по которому протекает ток. Влияние является противоположным направлению изменения тока. То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.

Индуктивное сопротивление зависит от частоты тока. Чем она выше, тем выше скорость изменения данного параметра. Это значит, что будет образовано более сильное магнитное поле. Возникающая при этом ЭДС препятствует изменению электрического тока.

Расчет реактивного индуктивного сопротивления осуществляется по такой формуле:

XL = L×w = L×2π×f, где буквами обозначаются:

• L — индуктивность магнитного поля, которое порождается изменением силы тока;
• W — круговая частота изменения, которая используется в описании синусоидального изменения силы тока;
• Π — число «пи»;
• f — частота тока в обычном смысле.

При синусоидальном изменении напряжения сила тока будет меняться, отставая от него по фазе. Поэтому реактивное сопротивление трансформатора существенно зависит от его индуктивности.

Какое сопротивление называется реактивным, какое активным

Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.

Типы рассматриваемой величины и формулы ее расчета

Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.

Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сети

Различия между активным и реактивным сопротивлением

Разница между активным и реактивным сопротивлением состоит в том, что при прохождении электротока по компонентам цепи, несущим активную нагрузку, имеют место мощностные потери в виде выделения тепла, которое не может быть снова превращено в электрическую энергию. В качестве наглядного примера можно привести конфорку электроплиты, выделяющую тепловую энергию. Такими свойствами обладают и осветительные устройства, электрические двигатели, различные кабели. Фазы проходящих через такие компоненты напряжения и электротока будут совпадать.

Будет интересно➡ Замена штекера зарядки mini usb на micro usb. Микро усб схема распайки зарядки. Распиновка micro usb 5 pin для зарядки

От чего зависит сопротивление проводника

Реактивные нагрузки отличаются наличием емкостных свойств либо способностью к индукции. В первом случае величина рассматриваемого сопротивления зависит от емкости, во втором – от электродвижущей силы самоиндукции.

Важно! Величина, в противоположность активной, может иметь плюсовой и минусовой знаки. Это зависит от того, в какую сторону идет фазовый сдвиг. При опережении электрическим током напряжения будет иметь место отрицательный показатель, в обратном случае – положительный.

Какие отличия

Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.

Индуктивная величина и ее формулы

Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.

Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.

Комплексная сопротивляемость отдельного элетроэлемента сети R

В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.

Активная сопротивляемость в цепи переменного синусоидального тока

Области проявления

Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.

Вам это будет интересно Особенности активно-емкостной нагрузки

Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.

Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.

Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.

Индукция ЭДС может наблюдаться в дросселе

Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.

Переменный ток

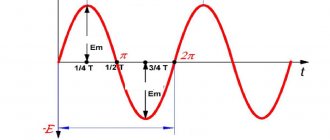
Для того чтобы понять, что такое активное сопротивление, необходимо разобраться в самом явлении переменного тока. Переменным является такой тип тока, который непрерывно изменяет направление своего протекания. Во время протекания потенциалы переменного тока постоянно изменяются. Это происходит благодаря работе генератора, а точнее за счет взаимодействия магнитного поля с медной обмоткой. Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.

Будет интересно➡ Способы подключения асинхронного электродвигателя

Роль переменного тока сложно переоценить. Главное его достоинство заключается в простоте передачи от источника к потребителю, возможность занижать или увеличивать напряжение при помощи трансформаторов. Также, переменные электрические токи можно доставлять потребителю с гораздо меньшими затратами.

Активное сопротивление

Переменный ток доставляется потребителю с целью его преобразования в иные виды энергии, например, тепло и свет. В бытовых сетях преобладает использование однофазного переменного тока. При подключении потребителя создается активное сопротивление.

Простые цепи переменного тока с активным сопротивлением включает в себя генератор тока и идеальный резистор. При этом должны соблюдаться необходимые условия для идеальной цепи:

1. Активное сопротивление не должно равняться нулю, обязательное условие.
2. Емкость и индуктивность цепи должны быть равны нулю.

Также, для идеального активного сопротивления должны соблюдаться следующие условия:

1. Соблюдаются закон Ома для мгновенных, среднеквадратичных и амплитудных параметров цепи.
2. Значение полностью независимо от амплитудных колебаний.
3. Между током и напряжением отсутствует сдвиг фаз.
4. Элемент, находящийся под напряжением, выделяет долю тепловой энергии, то есть нагревается.

Все эти условия позволяют электрическим приборам работать в пределах точно установленных параметров с максимальным КПД. Любое изменение может быть причиной отсутствия надежного контактного соединения или неисправностью самого потребителя.

Для того чтобы рассчитать величину активного сопротивления в цепи, необходимо знать величину напряжения и силы тока. Для расчета используется формула: R=U/I. Формула состоит из следующих значений:

1. «R» — сопротивление, Ом;
2. «U» — величина напряжения, вольт;
3. «I» — величина силы тока, ампер.

Далее можно сделать простой расчет. В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:

1. Напряжение цепи 240 вольт.
2. При замере силы тока получено значение 4 ампера.
3. R= 240/4=60 Ом.

Расчетная величина активного сопротивления — это не окончательное значение. На нее влияет прежде всего сечение проводов включенных в цепь, схема взаимодействия между цепями емкостных и полупроводниковых элементов.

Активное значение цепи также вызывает безвозвратную потерю первоначальной электрической энергии, а так же приводит к снижению мощности.

Полное сопротивление

При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах. Оно способствует превращению части электрической энергии в нагрев. Реактивное сопротивление возникает лишь в цепи переменного тока. Чтобы определить его величину, необходимо из индуктивного вычесть ёмкостное. Эта характеристика показывает энергию, которая пульсирует в цепи, переходя из одной формы в другую.

Полное сопротивление представляет собой сумму активного и реактивного сопротивления в цепи переменного тока, но такое сложение необходимо выполнять особым образом. Для этого нужно начертить прямоугольный треугольник, катеты в котором должны иметь длину, равную величине активного и реактивного сопротивлений соответственно.

Длина гипотенузы будет численно выражать полное сопротивление электрической цепи. Для его определения используется правило, говорящее о том, что сумма квадратов катетов равна квадрату гипотенузы. Это правило называют теоремой Пифагора. Следовательно, формула, с помощью которой можно найти полное сопротивление, выглядит так:

Z = √(R^2+〖(XL-XC)〗^2 ), где

• Z — полное сопротивление;
• R — величина активной составляющей;
• XL и XC — значение индуктивного и емкостного параметра соответственно.

Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.

Зависимость

Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.

Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.

Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.

Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.

Мгновенная мощность в цепи переменного тока с активным сопротивлением.

При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt

Из тригонометрии найдём

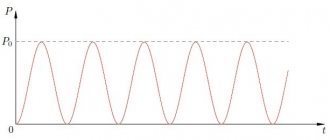
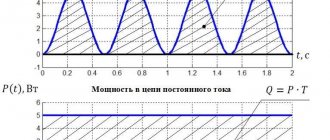
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2,то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:

Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р= UmIm√2 и перемен- ной р’:

р = Р + р’

Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.

Будет интересно➡ Напряжение в сети

Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.

Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.

Как рассчитать емкостное реактивное сопротивление

Рассмотрим пример расчета емкостного реактивного сопротивления: предположим, что конденсатор 6 мкФ подключен к розетке переменного тока с напряжением 40 В и частотой F 60 Гц.

Для определения емкостного реактивного сопротивления используется определение, данное в начале. Угловая частота ω определяется как:

ω = 2πf = 2π x 60 Гц = 377 с-1

Будет интересно➡ Витая пара: категории, обжим, советы по работе

Затем этот результат подставляется в определение:

ИксC = 1 / ωC = 1 / (377 с-1х 6 х10 -6 F) = 442,1 Ом

Теперь посмотрим на амплитуду тока, циркулирующего в цепи. Поскольку источник предлагает напряжение амплитудой VC = 40 В, мы используем соотношение между емкостным реактивным сопротивлением, током и напряжением для вычисления амплитуды тока или максимального тока:

яC = VC / ИКСC = 40 В / 442,1 Ом = 0,09047 А = 90,5 м А.

Если частота становится очень большой, емкостное реактивное сопротивление становится небольшим, но если частота становится равной 0 и у нас есть постоянный ток, реактивное сопротивление стремится к бесконечности.

Активная мощность для цепи переменного тока с активным сопротивлением

Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.

Активная мощность — среднее арифметическое мгновенной мощности за период.

Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).

Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.

В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:

P = UI

Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:

P = UI = I2R

С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].

Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:

Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.

Похожие темы:

[ads-pc-1]
Ток и напряжение.

При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uтsin ?t, то ток i также изменяется синусоидально:

i = Iтsin ?t

При этом

Iт= Uт/ R

Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис.

175,б). Следовательно,при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).

Если обе части равенства Iт= Uт/ Rразделить на ?2, то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:

I = U / R

Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.

Электрическая мощность.Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см.

рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t.

Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения.

Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°

Pmax= UтIт= 2UI

Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)

Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср= Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:

W = Pt.

Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому

P = Pmax/ 2 = UI

Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.

В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.

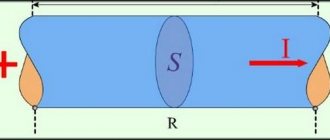
Поверхностный эффект. Следует отметить, что активное сопротивление проводников в цепи переменного тока всегда больше их сопротивления в цепи постоянного тока.

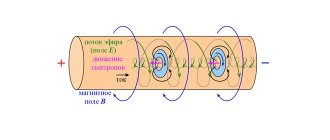
Переменный ток i не протекает равномерно по всему поперечному сечению проводника, как постоянный ток i, а вытесняется на его поверхность (рис. 176, а). Поэтому полезное сечение проводника как бы уменьшается и сопротивление его при переменном токе возрастает.

Это явление носит название поверхностного эффекта. Неравномерное распределение переменного тока по поперечному сечению проводника объясняется действием э. д.

с. самоиндукции, индуцированной в проводнике магнитным полем, которое создается проходящим по проводнику током I. Это магнитное поле действует не только в пространстве, окружающем проводник (внешний поток Ф2), но и внутри самого проводника (внутренний поток Ф2) (рис.

176,б). Поэтому слои проводника, расположенные ближе к его центру, будут охватываться большим магнитным потоком, чем слои, расположенные ближе к его поверхности, и э. д.

с. самоиндукции, индуцированная во внутренних слоях, будет большей, чем во внешних. Поскольку э.

д. с. самоиндукции препятствует изменению

Рис. 176. Схема протекания постоянного I и переменного i токов по проводнику (а) и возникновение поверхностного эффекта (б)

Рис. 177. Схема термообработки деталей токами высокой частоты: 1 — высокочастотный индуктор; 2 — закаливаемая деталь; 3 — разогретый слой

тока, последний будет стремиться пройти там, где э. д.

с. самоиндукции имеет наименьшее значение, т. е.

пройдет преимущественно по поверхностным слоям проводника. В результате этого плотность тока У в поверхностных слоях будет больше, чем во внутренних. Чем больше частота тока, тем больше э.

д. с. самоиндукции индуцируется во внутренних слоях проводника и тем в большей степени ток вытесняется на поверхность.

При частоте 50 Гц увеличение сопротивления медных и алюминиевых проводников при малом их диаметре практически ничтожно, и сопротивление таких проводников в цепях переменного и постоянного тока можно считать одинаковым. Но для медных и алюминиевых проводников диаметром свыше 10 мм, а для стальных проводников при еще меньших диаметрах необходимо при расчетах учитывать влияние поверхностного эффекта на их активное сопротивление.

При токах высокой частоты, принятых в радиотехнике, телевидении и различных высокочастотных установках, с целью лучшего использования металла проводников их обычно изготовляют полыми.

На свойстве переменного тока высокой частоты протекать, главным образом, по поверхности проводников основаны различные методы высокочастотной закалки и термообработки.

Например, при высокочастотной термообработке деталей вихревыми токами (рис. 177) эти токи индуцируются в основном в поверхностном слое металла. Они быстро разогревают поверхностные слои обрабатываемой детали, раньше, чем ее внутренняя часть успеет заметно нагреться за счет теплопроводности металла.

[ads-pc-2]

В электрической цепи переменного токасуществует два вида сопротивлений:активноеи реактивное. Это является существенным отличием от цепей постоянного тока.

В чем измеряется реактивное сопротивление

Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.

Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.

Емкостное сопротивление

Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.

После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.

Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.

Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.

На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.

Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:

XС = 1/(w×C) = 1/(2π×f×C), где

• C — ёмкость используемого конденсатора;
• w — круговая частота переменного тока;
• π — число «пи»;
• f — частота переменного тока.

В рассматриваемом случае изменения тока отстают от напряжения.

Как правильно измерять сопротивление

При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.

Косвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра. Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².

Приложения с емкостным реактивным сопротивлением

Фильтры верхних частот, фильтры нижних частот, мостовые схемы для измерения емкости и индуктивности и схемы фазового сдвига являются одними из основных применений схем, которые содержат емкостные реактивные сопротивления в сочетании с индуктивностями и электрическими сопротивлениями.

В стереосистемах некоторые динамики поставляются с отдельными динамиками. вуфер (больше) для низких частот и твитер или небольшой рог для высоких частот. Это улучшает производительность и качество звука.

В них используются конденсаторы, которые предотвращают попадание низких частот в высокочастотный динамик, а в низкочастотном динамике добавлен индуктор, чтобы избежать высокочастотных сигналов, поскольку индуктивность имеет реактивное сопротивление, пропорциональное частоте: XL = 2πfL.

Катушка

Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:

1. За счет индуктивности ограничивается скорость изменения токов.
2. С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
3. Создает магнитное поле.
4. Увеличивает и накапливает напряжение.
5. Создает сдвиг фаз переменного тока.
6. Пропорционально скорости движения тока создает ЭДС самоиндукции.

Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.

Принцип работы

Катушка индуктивности работает только при прохождении электрического тока через набор витков обмотки. При подключении элемента к электрической цепи, по витку начинает двигаться ток. За счет взаимодействия провода с металлическим сердечником создается магнитный поток. Поток полностью пропорционален индуктивности катушки и величине тока. Величину магнитного потока можно рассчитать по следующей формуле: Ф=L×I.

Элементами формулы являются:

1. «Ф» — величина магнитного потока.
2. «L» — индукция.
3. «I» — величина тока.

Количество витков влияет на величину ЭДС самоиндукции. Витки взаимодействуют не только с сердечником, но и между собой, что приводит к увеличению ЭДС.

В цепи переменного напряжения, величина ЭДС способна спровоцировать разность фаз напряжения и тока вплоть до 90 градусов.

Конструкция и разновидности

Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.

1. Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
2. Тороидальная. В такой катушке соленоид выполнен в форме «тора».
3. Многослойный тип, имеет несколько рядов обмотки.
4. Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
5. Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.

Индуктивность

Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:

1. Числа витков.
2. Сечения и длины провода.
3. Конструктивных особенностей детали.
4. От материала, длины, диаметра и формы сердечника.
5. От расстояния между витками.
6. Наличия экрана.

В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.

Замер сопротивления и формула расчета

Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.

1. Мультиметр надо перевести в режим омметра.
2. Красный измерительный щуп соединить с первым выходом катушки.
3. Черный измерительный щуп соединить со вторым выходом.
4. Прибор покажет только активное сопротивление обмотки.

При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.

Будет интересно➡ Резонанс напряжений. Где используется явление резонанса напряжений?

Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.

Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:

Z= 2×(R×R+XL×XL)

В этом выражении R является активным сопротивлением, а XL — индуктивным.

Емкостная проводимость линий

Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.

Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:

Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.

Емкостная проводимость одноцепной воздушной линии определяется по формуле:

Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.

Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:

Где: U – линейное напряжение сети, В; l – длина линии, км;

Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ. При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.

В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:

• Для воздушной линии:

• Для кабельной линии:

Активное сопротивление катушки

Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.

Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля. Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.

Скин-эффект

В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.

Провод литцендрат

Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.

Определение активного сопротивления проводов

Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые. Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:

где:

• γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
• s – номинальное сечение провода(кабеля),мм2;
• l – длина линии, м;
• ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].

Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].

Ёмкостное сопротивление

Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

Мы можем использовать следующие соотношения:

Попробуй обратиться за помощью к преподавателям

Если $I(t)$ определена уравнением (1), то заряд выражен как:

где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:

Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac<2>.$ Амплитуда напряжения на емкости равна:

Величину $X_C=frac<1>$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.