Индуктивность контура — теоретические основы
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
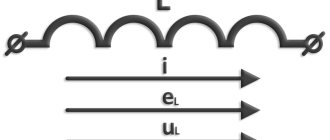
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
Напряжение на индуктивности уравновешивает ЭДС и может быть записано в виде uL=-eL=dΨ/dt=L×di/dt.
Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Проводник в электрическом поле
Помещая проводник в электрическое поле, носители заряда внутри проводника начинают перемещаться. Причем данное перемещение подчиняется двум правилам:
- Напряжённость электрического поля внутри проводника должно равняться нулю
Это означает, что потенциал внутри проводника остается постоянным (φ = const).
- Напряжённость поля на поверхности проводника направлена перпендикулярно к самой поверхности данного проводника. Или другими словами поверхность проводника становится эквипотенциальной, то есть все точки данной поверхности имеют одинаковый потенциал.
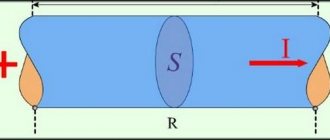
Из этих двух правил следует, что когда проводник вносится в электрическое поле его носители заряда (в металлах это электроны, а в жидкостях – ионы) приходят в движение, причем положительные по направлению напряжённости электрического поля, а отрицательные в противоположную сторону. Результатом движения зарядов в проводнике является возникновение зарядов противоположного знака на концах проводника, такие заряды называют индуцированными. Перераспределение заряда в проводнике показано на рисунке ниже
Распределение носителей зарядов проводника в электрическом поле.
Таким образом, нейтральный проводник, помещённый в электрическое поле, как бы разрывает часть линий электрического поля, а индуцированные заряды распределяются по поверхности проводника.
Практический интерес представляет следующая ситуация, когда внутри проводника имеется некоторая полость. Так как индуцирование зарядов происходит на поверхности проводника, то внутри этого проводника, а значит и во внутренней полости электрическое поле обращается в нуль. На данном явлении основана электростатическая защита, когда необходимо защитить какой-нибудь прибор от воздействия электрического поля, то его помещают внутрь экрана из проводника. Индуцированные заряды на поверхности экрана скомпенсируют электростатическое поле. Вместо сплошного экрана часто используют экран из электропроводящей сетки, что тоже позволяет создать защиту от электростатического поля.
Как найти индуктивность контура
Формула, которая является простейшей для нахождения величины, следующая:
- L = F : I,
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
- Ei = -L х dI : dt.
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
- W = L I2 : 2.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
- L= µ0n2V,
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
- L = µ0N2S : l,
Будет интересно➡ Правило буравчика
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Обозначение и единицы измерения
Сопротивление тока: формула
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.
Джозеф Генри
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Содержание
- 1 Вопросы и задачи
- 2 Микроопыт
- 3 Любопытно, что…
- 4 Что читать в «Кванте» о емкости и индуктивности
- 5 Ответы 5.1 Микроопыт
По существу, Вольта и Ленц упоминают известные вам устройства — конденсатор и соленоид, характеристиками которых являются емкость и индуктивность. Интересно, что если первый электрический конденсатор — лейденская банка — появился на свет, можно сказать, не специально, то соленоид был «открыт» Ампером в ходе целенаправленных опытов по исследованию магнитного действия электрического тока. Единицы измерения емкости и индуктивности впоследствии получили имена Фарадея и Генри, чем, надо полагать, физики не только отдали дань знаменитым ученым, но и подчеркнули важность этих понятий.
Безусловно, и емкости, и индуктивности можно было бы посвятить отдельные выпуски «Калейдоскопа». Но история науки распорядилась так, что им пришлось «поработать» и рука об руку. Как только выяснилось, что разряд лейденской банки, а затем и индукционной катушки, носит колебательный характер, в исследования колебательного контура включилась целая плеяда видных физиков — Гельмгольц, Томсон (лорд Кельвин), Кирхгоф и др. Увенчалось это «наступление» на колебательный контур открытием Герцем электромагнитных волн, что возвестило начало эпохи радио и телевидения. Какой бы областью электро-, радио- и телетехники сегодня мы ни заинтересовались, везде обнаружим либо сами конденсаторы и катушки, либо «отголоски» их присутствия в более совершенных приборах. Так происходит везде, где встречаются переменные токи и электрические колебательные процессы.
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C : (1 – 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
- Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
Конденсаторы с переменной емкостью
Изначально людям хватало описанных выше конденсаторов из пары пластин. Затем этот прибор получил своё развитие. Начали появляться устройства в виде шаров, дисков и цилиндров. Это было необходимо для того, чтобы повысить ёмкость конденсатора C, ведь она в первую очередь связана с площадью обкладок S и расстоянием между ними d. Это наглядно видно из формулы. По ней выполняется расчёт ёмкости конденсатора.
Ёмкость конденсатора
Эти нестандартные геометрические формы со временем перестали удовлетворять потребностям экспериментаторов. Поэтому были разработаны новые приборы с переменной ёмкостью. Они имеют подвижные пластины. Это позволяет легко менять площадь их взаимного пересечения, тем самым влияя на величину ёмкости конденсатора. Самый распространённый и всем знакомый пример данного электронного прибора – это колебательный контур в радио. Все люди хотя бы раз подстраивали приёмник. Именно эта «крутилка» есть переменный конденсатор. При ее вращении изменяется ёмкость, соответственно, резонансная частота колебательного контура радиоприёмника. Это, в свою очередь, настраивает радио на другую станцию.
Внешний вид переменного конденсатора
“Катушка ниток”
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
- I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от “витков в квадрате”.
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Будет интересно➡ Полное сопротивление
О применении керамических конденсаторов…
Рис.13. – из [11], стр.24. «Для других типов керамики, например Y5U или Y5V, значение Z, соответствующее резонансу, получается на значительно меньших частотах, что свидетельствует о худших свойствах конденсаторов с такими диэлектриками.»
– [10], стр.145.
Величина ESL от времени, температуры, и частоты не зависит (или эта зависимость пренебрежимо мала).
2.1.3. Сравнение ЭК и КК.
Как уже отмечалось выше, не все важные для разработки современных матплат параметры указываются в документации производителей конденсаторов. Поэтому воспользуемся данными корпорации «Интел», которая применяла при моделировании базового (референсного) дизайна МВ для чипсета I845G следующие параметры:
Таблица 3.
| Конденсатор, емкость | ESR | ESL | Примечание |
| OSCON, 560 мкФ | 9.28 mОм, max | 6.4 нГн, max | 1 |
| Алюминиевый ЭК 3300 мкФ | 12 mОм | 5 нГн | 1 |
| MLCC, корпус 1206, 10 мкФ | 3.5 mОм, тип. | 1.15 нГн, тип. | 1 |
Примечание 1 к таб. 3 – значения ESR и ESL основаны на значениях, используемых Интелом для моделирования распределения питания и не являются данными производителей.
– [7], стр.66. Из таб. 3 видно, что КК большой ёмкости обладают в несколько раз меньшими паразитными ESR и ESL, чем у ЭК. Кроме того, гораздо меньшие габаритные размеры КК позволяют использовать параллельное включение нескольких десятков КК, что приводит к соответствующему уменьшению ESR и ESL. Однако, значительно меньшая емкость КК не позволяет обойтись совсем без ЭК.
2.2. Условия работы конденсаторов в цепях питания ядра процессора.
Основное допущение, сделанное автором при дальнейшем изложении, состоит в том, что физическая суть эффектов в цепях питания от выходного дросселя конвертера до кристалла микропроцессора одинакова для любого из относительно нестарых процессоров от Intel Pentium-III до Intel Core Duo. Отличия только в количественных характеристиках и степени влияния этих эффектов на работоспособность и долговечность электролитических конденсаторов и процессора. Эти отличия связаны с тем, что для более новых процессоров: а) выше средний и максимальный потребляемый ток, из-за чего возрастают омические потери на паразитных сопротивлениях компонентов источника питания, токопроводящих дорожек системной платы, контактов процессорного разъема; б) выше скорость переходных процессов на шинах питания, из-за чего растут выбросы и просадки напряжения на паразитных индуктивностях компонентов источника питания, токопроводящих дорожек системной платы, контактов процессорного разъема; в) ниже номинальное напряжения питания ядра процессора, из-за чего понижается запас помехоустойчивости – это вынуждает ужесточать требования к стабильности напряжения питания и устойчивости к дестабилизирующим факторам, перечисленным выше. С учётом сказанного, попытаемся проанализировать документацию на процессоры в указанном «диапазоне».
2.3. Требования к цепям питания. Попытаемся выяснить, почему и какие требования предъявляются производителем процессоров к цепям питания и ШИМ-конверторам. Будем опираться на документацию фирмы INTEL, как производителя наиболее высокочастотных процессоров, для которых изучаемые эффекты могут иметь наибольшее значение.
«Из-за очень большого числа транзисторов и высокой внутренней частоты тактирования процессор способен производить большие колебания среднего тока между состояниями низкой и полной загрузки»
— [12], стр.19.
«Неизбежная индуктивность проводов и шин питания снижает возможность источника питания быстро реагировать на переходные процессы по току. Блокировка (Decoupling) шин питания может быть охарактеризована несколькими особенностями
[в оригинале – «зонами интересов»].
Чем ближе к нагрузке расположены конденсаторы, тем бОльшая индуктивность будет обойдена. Для обхода индуктивностей паек, шин питания и т.п. требуется меньшая ёмкость. Таким образом, близость [конденсаторов] к нагрузке [требует] меньше места для их размещения. <�…> Время реакции конвертера по цепи обратной связи намного дольше, чем время, за которое изменение нагрузки процессора вызывает [переходной] эффект. Это особенно верно, если изменение нагрузки произошло с высокой скоростью. Батарея (bulk) [электролитических] конденсаторов снабжает энергией истощенные высокочастотные блокирующие [керамические] конденсаторы до времени, когда источник питания сможет отреагировать. Вернее, батарея [электролитических] конденсаторов снижает требования к источнику питания по переходным процессам до значений, которые он в состоянии обеспечить. <�…> Высокочастотные [керамические] блокирующие конденсаторы должны располагаться настолько близко к питающим выводам процессора, насколько это физически возможно. Это жизненно необходимое требование, т.к. индуктивность шин питания на плате может свести на нет пользу от применения этих низкоиндуктивных компонентов.»
— [13], стр.33,34.
«К примеру, <�…> 250 пикоГенри [паразитной] индуктивности обычно игнорируются в системах распределения питания, пока не появятся перепады тока со скоростью изменения в 1 А/нс, которые имеются при использовании процессора Pentium-III. Падение напряжения на индуктивности в этом случае может составить 250 мВ.»
— [14], стр. 9.
«Зона <…> регулирования ШИМ <…> определена как полоса частот регулятора с замкнутой цепью обратной связи. Типичное значение — 30-40 кГц для 300-килогерцового регулятора.»
— [15], стр. 26.
«Обычный конвертер имеет время реакции в пределах от 1 до 100 мкс, в то время как перепады тока потребления процессора занимают от 1 до 20 нс»
— [14], стр.19. (Обратите внимание, какие высокие скорости изменения тока были у слотовых 500-мегагерцовых (!) процессоров в 1999 году! По всей видимости имелось в виду, что для данных процессоров такое значение скорости было бы в отсутствие блокирующих керамических конденсаторов возле кристалла процессора.) Читаем там же:
«Для Pentium-III перепады тока, вызванные изменением нагрузки, могут быть 15,3 А или выше. Это не только быстрые изменения потребляемого тока, но и длительные периоды среднего потребляемого тока. Заметьте, даже при выполнении обычных операций потребности в токе могут изменяться на 7 А или более из-за смены активных уровней внутрипроцессорных логических элементов (компонентов).»
— [14], стр.19. Скачок тока потребления на семь или более ампер за одну или несколько наносекунд невозможно обеспечить без блокирующих керамических конденсаторов непосредственно возле кристалла процессора, т.к. ток через шины питания просто не успеет вырасти из-за существенной на таких скоростях паразитной индуктивности проводников. Таким образом, у автора сложилось мнение, что керамические конденсаторы возле сокета и непосредственно на процессоре выполняют роль накопителей энергии, которой они обеспечивают ядро процессора до тех пор, пока ток через паразитные индуктивности не возрастет до нужного значения. К сожалению, полной определенности в этом вопросе нет, частично и из-за позиции . Вот как были определены понятия «пульсации» и «шумы»:
«Выходные пульсации и шумы определены как периодический или случайный сигнал в диапазоне частот до 20 МГц на выходе [источника питания] под постоянной нагрузкой
.
(Выделено и подчеркнуто мною – Я.М.)» — [6], стр. 14. Т.е. перепады тока от изменения
загрузки процессора под данное определение не подпадают. В последующем терминология Интел изменилась, фактически противореча процитированному определению:
«Выходной фильтр содержит высокочастотные блокирующие [керамические] конденсаторы для гарантированного подавления пульсаций и шумов корпуса до определённых уровней.»
– [16], стр. 35. Скорее всего, по мнению автора, это связано с тем, что в рекомендациях последних лет для разработчиков вместо формул и примеров расчетов приведены конкретные числовые значения (количество, номинал, максимально допустимые ESR и ESL, место размещения для электролитических и керамических конденсаторов), соответственно, отпала надобность в подробном рассмотрении физических процессов на шинах питания.
«В связи с тем, что электролитические блокирующие конденсаторы обладают не только ESR, но и довольно высокой индуктивностью, эти конденсаторы нуждаются в помощи других конденсаторов, имеющих меньшую индуктивность (но и, обычно, меньшую ёмкость). Эти высокочастотные [керамические] конденсаторы контролируют переключательные перепады и поддерживают шины питания при изменениях нагрузки, пока [электролитические] конденсаторы с бОльшей индуктивностью не смогут отреагировать.»
— [14], стр. 22 – такое объяснение 1999 года более содержательно раскрывает назначение КК, чем просто «гарантированное подавление шума».
2.4. Концепция модели.
В первом приближении модель системы питания выглядит, как изображено на рис.14:
Рис. 14. Здесь: источник напряжения V1
и дроссель
L1
– имитируют понижающий конвертер,
С1
– батарея электролитических блокирующих конденсаторов, установленных в непосредственной близости от выходного дросселя L1,
R1
и
L2
– паразитные ESR и ESL шин питания от С1 до С2 (проводники, пайки ),
С2
– батарея керамических блокирующих конденсаторов
возле процессорного разъёма
,
R2
и
L3
– суммарные паразитные ESR и ESL цепей питания от С2 до С3 (проводники, пайки, контакты разъёма, ножки (выводы) процессора, проводники в корпусе процессора от выводов до места расположения С3),
С3
– батарея керамических блокирующих конденсаторов
возле кристалла процессора
, расположенная непосредственно
на корпусе процессора
. Программируемый источник тока
CPU
имитирует потребление тока ядром процессора.
Работу схемы, с учетом сказанного выше, можно объяснить следующим образом: С3 поддерживает напряжение питания ядра процессора в допустимых пределах при скачках потребления, пока ток от С2 через R2L3 не изменится соответствующим образом. Основная причина замедленного изменения тока здесь – индуктивность L3. Дополнительно С3 подавляет до безопасного уровня шумы и наводки от работающего процессора. С2 выполняет ту же роль по отношению к С3, пока ток от С1 через R1L2 не изменится. Основная причина замедленного изменения тока здесь – индуктивность L2 и паразитная внутренняя последовательная индуктивность ЭК С1, не показанная на схеме. Также С2 разгружает С1 от скоростных перепадов тока (тем самым уменьшая выделяющуюся на нём мощность, т.е. снижая нагрев ЭК) и дополнительно ослабляет шумы и наводки. С1 поддерживает напряжение питания всех последующих цепей в допустимых пределах, пока конвертер не отреагирует на изменение тока потребления. Основная причина замедленного изменения тока здесь – время реакции конвертера на изменение тока нагрузки. Это хорошо иллюстрирует рис.15:
Рис.15 – из [17], стр.25.
3. Схемотехническое моделирование в программе Micro-Cap 8.
Поставим себе цель выяснить, как зависят размах пульсаций питающего напряжения непосредственно на кристалле процессора Vcpu и мощность, рассеиваемая на ЭК от количества и места подключения КК.
3.1. Схемы для моделирования.
При выборе схемы для моделирования автор статьи исходил из следующих соображений: а) в большинстве плат под mPGA478, так же, как и под LGA775, применяются многофазные ШИМ–конвертеры (2…4-фазные); б) паразитные параметры медных печатных проводников не существенно зависят от типа применяемого процессора. А учесть разводку какой-то конкретной платы затруднительно, в т.ч. и по причине наличия внутренних слоёв. По крайней мере, если задаться целью только выяснить степень влияния емкости и расположения КК на тепловыделение в ЭК, эту часть схемы можно оставить неизменной; в) примерные соотношения между паразитными параметрами различных процессорных разъёмов можно определить из таблиц 4 и 5, и при проведении моделирования для конкретного разъёма следует изменить номиналы соответствующих элементов схемы; г) для моделирования поведения схемы с конкретным процессором необходимо задать параметры перепада тока (для источника тока I_PWL) в соответствии с быстродействием и максимальным/минимальным потреблением данного процессора; эти параметры приводятся в справочных данных производителя процессора. Поэтому за основу была взята схема, предложенная в [15], стр.71-79. Доработанный вариант схемы представлен на рис.16. По сравнению с оригинальной схемой был изменен номинал R1 и удалены элементы, моделирующие паразитные параметры лабораторного инструмента (внешнего нагрузочного устройства и адаптера-позиционера). Добавлены модели конденсаторов CDOP1, CDOP2, CCPU1, выключатели S1…S3, источники напряжения V1, V2 и их выходные дроссели LVR1, LVR2. Для моделирования платы с однофазным конвертером под PGA-370 можно использовать упрощенный вариант схемы на рис.17. Следует отметить следующие недостатки используемой модели: – в обеих схемах использованы простейшие 3-элементные схемы замещения ЭК и КК, не учитывающие изменений основных параметров конденсаторов с температурой, напряжением, частотой; – схемы не учитывают ограниченное быстродействие ШИМ-конвертера, поэтому в реальности выделяемая на ЭК мощность гораздо выше; – в схемах не учитываются паразитные параметры соединений
между
ЭК в батарее; – в реальных процессорах возле кристалла расположены специальные КК меньшей ёмкости со значительно пониженной индуктивностью и сопротивлением, поэтому в реальности пульсации подавляются
лучше
, чем показывает моделирование.
Рис.16.
Рис.17.
3.2. Описание схемы (рис.16).
V1, V2 – источники постоянного напряжения 1,5 В; LVR1 – выходная катушка индуктивности (дроссель) первого понижающего преобразователя (VR1); LVR2 – выходной дроссель второго понижающего преобразователя (VR2); CMB1, RMB1, LMB1 – соответственно суммарные ёмкость, эффективное последовательное сопротивление (ESR), эквивалентная последовательная индуктивность (ESL) батареи электролитических конденсаторов на выходе VR1; CMB3, RMB3, LMB3 – то же самое на выходе VR2; CDOP1, RDOP1, LDOP1 – соответственно суммарные ёмкость, ESR, ESL дополнительных керамических конденсаторов, подпаиваемых к выводам электролитических конденсаторов на выходе VR1 (можно отключить выключателем S2); CDOP2, RDOP2, LDOP2 – то же для VR2 CMB2, RMB2, LMB2 – соответственно суммарные ёмкость, ESR, ESL батареи керамических многослойных (MLCC) конденсаторов, расположенных в непосредственной близости от процессорного разъёма – сокета (можно отключить выключателем S1); RMB101 и LMB101 – паразитные сопротивление и индуктивность проводников от выходного дросселя VR1 до точки подключения сокета (с «северной» стороны); RMB105 и LMB105 – то же для VR2 с «южной» стороны сокета; RMB102 и LMB102 – паразитные сопротивление и индуктивность проводников от точки подключения сокета с «северной» стороны до середины центрального выреза в сокете; RMB104 и LMB104 – то же с «южной» стороны; RMB103 и LMB103 – паразитные сопротивление и индуктивность проводников от середины центрального выреза в сокете до точки подключения с «южной» стороны сокета; RSKT1, LSKT1 – паразитные сопротивление и индуктивность «северного» сегмента сокета; RSKT2, LSKT2– то же для центрального сегмента сокета; RSKT3, LSKT3– то же для «южного» сегмента сокета; CCPU1, RCPU1, LCPU1 – соответственно суммарные ёмкость, ESR, ESL керамических конденсаторов, расположенных непосредственно на процессоре (можно отключить выключателем S3). Параметры контактов сокета и выводов процессора. Таблица 4. Индуктивность.
| Разъём | Индуктивность одной пары контактов (Lпары) | Число контактов Vcc (NVcc) | Число контактов Vss (NVss) | Общая индуктивность (Lобщ.) | Ссылка на первоисточники |
| PGA370 | 3,5 нГн | 74 | 74 | 47 пГн | [18, 12] |
| mPGA478 | 3,3 нГн | 85 | 180 | 29 пГн | [19, 20] |
| LGA775 | 3,9 нГн | 226 | 273 | 15 пГн | [21, 22] |
Таблица 5. Сопротивление.
| Разъём | Сопротивление одной пары контактов (max) (Rпары) | Число контактов Vcc (NVcc) | Число контактов Vss (NVss) | Общее сопротивление (Rобщ.) | Ссылка на первоисточники |
| PGA370 | 25 mОм | 74 | 74 | 0,3 mОм | [18, 12] |
| mPGA478 | 25 mОм | 85 | 180 | 0,2 mОм | [19, 20] |
| LGA775 | 28 mОм | 226 | 273 | 0,1 mОм | [21, 22] |
Примечания к таб. 4 и 5 : 1. Число контактов питания (Vcc) и земли (Vss) может варьироваться в небольших пределах в зависимости от модели процессора. 2. Общие индуктивность и сопротивление вычислялись с последующим округлением по формулам: Lобщ. = Lпары / NVcc / 2 + Lпары / NVss / 2, Rобщ. = Rпары / NVcc / 2 + Rпары / NVss / 2.
3.3. Результаты моделирования.
Проведём моделирование для конфигурации, состоящей из 2-фазного ШИМ-конвертера и процессора Пентиум-4 3000 МГц (см. рис.16). Параметры фильтра оставим прежними (принятые для более мощных процессоров в LGA775-корпусе, они с запасом должны удовлетворять потребности выбранного процессора). Для возможности пошагового варьирования параметров отметим, что батареи ЭК (СМВ1 и СМВ3) составлены соответственно из шести и четырёх ЭК ёмкостью по 560 мкФ , ESR=6 мОм, ESL=3,3 нГн. Параметры одного КК: С=10 мкФ , ESR=2,88 мОм, ESL=1080 пГн. Для удобства параметры батарей таких конденсаторов сведены в таблицу 6: Таблица 6.
| С, мкФ | 10 | 20 | 40 | 60 | 100 |
| ESR, мОм | 2,88 | 1,44 | 0,72 | 0,48 | 0,288 |
| ESL, пГн | 1080 | 540 | 270 | 180 | 108 |
Паразитные параметры контактов сокета RSKT1…RSKT3 и LSKT1…LSKT3, в соответствии с таблицами 4 и 5 увеличим в 2 раза по сравнению с исходными, соответствующими разъёму LGA775. Осталось решить вопрос с величиной и длительностью испытательного перепада тока. В руководствах по разработке конвертеров питания ядра процессоров Пентиум-3 ([6], стр.14) и Пентиум-4 ([23], стр.11 и [17], стр.7) приведены параметры перепадов тока в некоторых наихудших стечениях обстоятельств – см. рис.18 и примечания к нему.
Примечания к рис.18: – Продолжительность периодов максимальной и минимальной нагрузки зависят от быстродействия процессора: более быстрый процессор имеет меньшую продолжительность. – Другие управляемые операционной системой события могут иметь время нарастания от 700 тактов. – Наихудшее стечение обстоятельств может заставить ток потребления процессора совершить цикл переходов 100% –> 40% –> 100% за 30-50 тактов.
Рис. 18
— из [17], стр.7. Запрограммируем источник тока I_PWL для имитирования одного периода перепада, показанного в верхней части рис.18. Выражение будет иметь вид (в одну строку): pwl 0,0 0.3u,3.24 0.300333u,25.92 0.301998u,32.4 0.385248u,32.4 0.391908u,64.8 2.591908u,64.8 2.592241u,25.92 2.592907u,32.4 2.726107u,32.4 2.72644u,3.24 4.82644u,3.24 1.3,0 Здесь: pwl — тип генератора, — программируемый источник постоянного тока (Constant current source); 0,0 — нулевые начальные значения (число слева от запятой — момент времени, а справа — соответствуещая этому моменту величина тока), применены для того, чтобы избежать «звона» модели, вызванного скачком тока с бесконечной скоростью при ненулевом токе в нулевой момент времени; 0.3u,3.24 — относительно плавное (на протяжении почти 1000 тактов) линейное нарастание тока процессора до минимального значения (согласно рис.18 — 5% от максимального тока, для выбранного процессора Imax=64,8 А); 0.300333u,25.92 — скачок от 5% до 40% за один такт (1 такт=0,333нс=333пс); 0.301998u,32.4 — скачок от 40% до 50% за 5 тактов (мы же рассматриваем наихудший вариант, поэтому выбираем наименьшее значение из вилки «5-10 тактов»); 0.385248u,32.4 — удержание тока на протяжении 250 тактов; 0.391908u,64.8 — скачок от 50% до 100% за 20 тактов; 2.591908u,64.8 — удержание тока на протяжении 2,2 мкс; 2.592241u,25.92 — спад тока от 100% до 40% за 1 такт; 2.592907u,32.4 — нарастание тока от 40% до 50% за 2 такта; 2.726107u,32.4 — удержание тока на протяжении 400 тактов; 2.72644u,3.24 — спад тока от 50% до 5% за 1 такт; 4.82644u,3.24- удержание тока на протяжении 2,1 мкс; 1.3,0 — плавный спад тока до нуля за гигантское, в масштабе исследуемого процесса, время 1,3 с.
Из документации на процессор выясним, что максимальный ток потребления выбранного процессора составляет 64,8 А. Время одного такта – 0,333 нс. 3.3.1. Влияние места подключения и ёмкости КК.
Разомкнём все выключатели (рис.16). Составим «тестовую» батарею КК 20 мкФ с параметрами согласно таб.6 и будем подключать её поочередно к точкам Vcpu (опыт 1), Vmlcc (опыт 2). Подключение к ЭК (СМВ1 и СМВ3) проведем в 3 вариантах – сначала по 10 мкФ (опыт 3), затем по 20 мкФ (опыт 4), потом смоделируем ситуацию, когда на выводы каждого отдельного ЭК напаян КК 10 мкФ (опыт 5). Результаты моделирования для каждого случая в порядке перечисления сведены в таб.7:
Таблица 7.
| № опыта | Точка подключения | Суммарная емкость КК, мкФ | Суммарная рассеиваемая на ЭК мощность, мкВт | Размах пульсаций, от пика до пика, В |
| 1 | Vcpu | 20 | 4,905 | 0,385 |
| 2 | Vmlcc | 20 | 4,519 | 2,7 |
| 3 | СМВ1 и СМВ3 | 20 | 8,817 | 2,9 |
| 4 | СМВ1 и СМВ3 | 40 | 5,485 | 0,068 |
| 5 | СМВ1 и СМВ3 | 100 | 3,010 | 1,597 |
Примечания к таблицам 7 и 8: – рассеиваемая на ЭК мощность вычислялась как интеграл по времени анализа (3,5 мкс); – размах пульсаций замерялся по построенному программой графику, причем пики и провалы шириной менее 100 нс игнорировались – такая возможность предоставлена корпорацией Интел в [15] на стр. 25; – в таблице 7 в строках 2, 3 и 5 размах пульсаций превышает напряжение питания – опечатки здесь нет, именно так и показывает Micro-Cap. Вызвано это тем, что, в отличие от реальной платы, мы отключили в модели все конденсаторы с целью определить наивыгоднейшую точку подключения КК.
С учетом результатов опытов 1…3 можно отметить, что в данном случае (т.е. в отсутствие других КК) при прочих равных условиях наибольшее снижение тепловыделения в ЭК дает подключение тестового конденсатора возле сокета процессора. Производители плат именно там и размещают все КК. Но из результата опыта 5 видно, что есть возможность к улучшению ситуации. (Резкое снижение пульсаций в опыте 4 (таб.7) связано, по видимому, с непреднамеренным резонансным эффектом в модели – не подлежит сомнению, что без конденсаторов на корпусе процессор работать не сможет.) Теперь определим, как поведет себя плата с уже смонтированными компонентами фильтров. Для выяснения этого замкнем в нашей модели выключатели S1 и S3 – тем самым мы приводим нашу модель к, казалось бы, «идеальному» (т.е. стандартному, рекомендованному изготовителем процессора) состоянию, и снова проведем моделирование. Вначале – совсем без «тестового» конденсатора («стандартный» отсчёт), а затем с поочередным подключением в уже перечисленном выше порядке. Результаты – в таблице 8:
Таблица 8.
| № опыта | Точка подключения | Суммарная емкость КК, мкФ | Суммарная рассеиваемая на ЭК мощность, мкВт | Размах пульсаций, от пика до пика, В |
| Стандартный | –––– | –––– | 1,009 | 0,12 |
| 1 | Vcpu | 20 | 0,943 | 0,15 |
| 2 | Vmlcc | 20 | 1,196 | 0,1 |
| 3 | СМВ1 и СМВ3 | 20 | 0,745 | 0,12 |
| 4 | СМВ1 и СМВ3 | 40 | 0,475 | 0,1 |
| 5 | СМВ1 и СМВ3 | 100 | 0,357 | 0,1 |
| Проверочный | Vmlcc | 100 | 5,02 | 0,08 |
Занятная ситуация! В этот раз наибольшее снижение выделяемой мощности происходит при подключении тестового конденсатора непосредственно к ЭК, а при подключении возле сокета наблюдается даже некоторое увеличение этого параметра! Но самое интересное – в результатах опытов 4 и 5 (таб. 8). Из них следует, что даже если компьютерная системная плата была разработана в полном соответствии с рекомендациями Интел, и производитель установил на плату все КК (что бывает очень и очень редко), можно снизить тепловыделение на ЭК не менее чем в 2,8 раза! И всех затрат при этом – цена КК в количестве, равном числу ЭК (или цена неисправной платы, с которой их можно выпаять). Но давайте проверим себя – быть может, эффект вызван простым увеличением (на 100 мкФ) общей емкости КК в цепи питания? Для этого отключим от ЭК наши тестовые конденсаторы и подключим к точке Vmlcc дополнительный КК ёмкостью 100 мкФ (остальные параметры – в таб.6). Более подробно смотрите в дополнении к статье. Результат – в нижней строке таб. 8 – позволяет сделать следующие выводы.
3.3.2. Выводы.
Во-первых, напайка КК на выводы ЭК необходима, т.к. реально позволяет в разы снизить выделяемую на них мощность (и соответственно повысить их долговечность). Во вторых, безоглядное увеличение сверх рекомендованной корпорацией Интел емкости КК возле сокета процессора может привести к противоположному результату – принцип «кашу маслом не испортишь» здесь неприемлем. В третьих, если на плате вокруг сокета процессора слишком много пустых посадочных мест под КК в корпусе 1206, стоит задуматься об их допайке на некоторые из этих мест. Но окончательное решение можно принимать только после того, как вы ознакомились с документацией на свой процессор, выяснили рекомендуемые фирмой Интел количество, размер и емкость КК и убедились, что на вашей плате их явно недостаточно.
4. Практические рекомендации по допайке КК на выводы ЭК.
На выводы каждого ЭК, стоящего перед и после каждого дросселя ШИМ-конвертера надо напаять один или несколько КК общей ёмкостью около 10 мкФ на один ЭК.
4.1. Подготовка.
Для удобства и безопасности (в плане сохранности системной платы) следует использовать маленькие вспомогательные платы 9 на 4 мм из односторонне фольгированного стеклотекстолита с отверстиями в соответствии с расстоянием между выводами конкретного ЭК. Автор использовал двухсторонний фолгированный стеклотекстолит и острым ножом расщепил его на два односторонних листа. Допустимая толщина заготовок определяется длиной выступающей части выводов ЭК над поверхностью системной платы, во многих случаях будет достаточно толщины 0,5 мм. Фольга между отверстиями на плате должна быть удалена (но не вся! только узкая полоса поперек линии, соединяющей отверстия), ширина разреза фольги 1 мм, эскиз приведен на рис. 19.
Рис. 19. На эти платы сначала напаиваем КК, затем надеваем платы на выводы ЭК и аккуратно пропаиваем.
4.2. Проведение работ.
ВАЖНО!!! Перед работой все комплектующие (процессор, память, платы расширения, кабели, батарейка и т.п.) с платы должны быть сняты.
Внимание! Если ЭК стоят в ряд и выводы у всех на одной линии, убедитесь, что вы не ошиблись и не надели плату на выводы разных соседних конденсаторов. Ещё раз Внимание! Платы следует устанавливать деталями и фольгой НАРУЖУ от системной платы!
Паять хорошо прогретым низковольтным паяльником с жалом, гальванически соединённым с общим проводом системной платы.
Каждый напаиваемый КК должен быть проверен на отсутствие короткого замыкания (КЗ). Каждая подсобранная вспомогательная плата должна быть проверена на отсутствие КЗ. После завершения напайки на выводы ЭК до подачи питания должна быть опять проведена проверка на отсутствие КЗ.
4.3. Включение и проверка.
Процедура известная, но всё же кратко о ключевых моментах. Только убедившись, что нигде нет короткого замыкания, можно подключить системную плату (без процессора и комплектующих!) к БП и попытаться её включить (берегите глаза! Всякое случается…). Если фейерверка не последовало, проверяем номиналы всех напряжений. Если всё в порядке — отключаем питание, устанавливаем только процессор и динамик и снова включаем питание. Если процессор стартовал и программа POST стала подавать характерные звуковые сигналы из-за отсутствия оперативной памяти — отключаем питание и устанавливаем остальные комплектующие.
5. Дополнения к статье.
Для удобства виртуального «экспериментирования» с моделью схема была дополнена. Чтобы не вносить каждый раз изменения в схему, лучше сразу предусмотреть все необходимые варианты, которые можно подключать, использую анимированные переключатели. Такой вариант схемы представлен на рис.20, а соответствующий схемный файл можно скачать по ссылке: https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26791&filename=mPGA478_4_5.zip
Рис.20. Цепочка С10 R112 L112 подключается переключателем S8 для выполнения опыта 1 по таб. 8. Цепочка С4 R106 L106 подключается переключателем S4 для выполнения опыта 2 по таб. 8. Цепочки С5 R107 L107 и С6 R108 L108 подключаются переключателем S5 для выполнения опыта 3 по таб. 8. Цепочки С7 R109 L109 и С8 R110 L110 подключаются переключателем S6 для выполнения опыта 4 по таб. 8. Цепочка С9 R111 L111 подключается переключателем S7 для выполнения опыта «Проверочный» по таб. 8.
можно в конференции (адрес именно такой, с кириллицей)
https://www.rom.by/forum/Электролитические_конденсаторы Автор данной статьи присутствует там под ником Ter_Abit.
Схемные файлы для программы Micro-Cap 8 (совместимы и с седьмой версией этой программы) доступны для скачивания в zip-архиве по ссылке: https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26654&filename=Ceramic_sch.zip Журнальный вариант статьи доступен для скачивания по следующим ссылкам: Часть 1 (djvu, 207 kB) — https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26655&filename=Ceramic_1.djvu; Часть 2 (pdf, 169 kB) — https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26653&filename=rh607_4750.pdf.
Автор выражает благодарность: – модераторам и участникам указанной конференции за конструктивное обсуждение, – А.Сорокину за содержащийся в его статье [1] толчок к размышлениям в правильном направлении, – С.А.Амелину (г. Смоленск) за консультации и помощь в освоении Micro-Cap.
Литература.
1. Сорокин А. Особенности применения оксидных конденсаторов в цепях питания микропроцессоров. — Радио, 2003, №1, с. 20 2. www.rom.by 3. ALUMINUM ELECTROLYTIC CAPACITORS CAT. No. E1001G (Ver.2). Nippon Chemi-Con. (al-productionguide-e-070315.pdf с сайта Nippon Chemi-Con). 4. Aluminum Electrolytic Capacitors General technical information. EPCOS.(PDF_GeneralTechnicalInformation.pdf с сайта EPCOS). 5. Aluminum Electrolytic Capacitors 10.2006. SANYO. (EC_E.pdf с сайта SANYO). 6. VRM 8.5 DC–DC Converter Design Guidelines (24965902.pdf, www.intel.com). 7. Intel® Pentium® 4 Processor in 478-pin Package and Intel® 845G/845GL/845GV Chipset Platform Design Guide (29865402.pdf, www.intel.com). 8. Solid Electrolytic Capacitors with Functional Polymer RE Series R5 Type. FUJITSU. (re-r5e.pdf с сайта FUJITSU). 9. Multilayer ceramic capacitors. General technical information. October 2006. EPCOS. (PDF_General.pdf с сайта EPCOS). 10. Мелешин В. Транзисторная преобразовательная техника. Издательство «Техносфера», 2005г. 11. Multilayer ceramic capacitors. Chip capacitors, Advanced series, C0G and X7R. October 2006 (AS_C0G_X7R_CC.pdf с сайта EPCOS). 12. Intel® Pentium® III Processor with 512KB L2 Cache at 1.13GHz to 1.40GHz (24965704.pdf, www.intel.com). 13. Low Voltage Intel® Pentium® III Processor 512K Dual Processor Platform Design Guide (27367401.pdf, www.intel.com). 14. Pentium® III Processor Power Distribution Guidelines Application Note. April 1999. (24508501.pdf, www.intel.com). 15. Voltage Regulator-Down (VRD) 11.0 Processor Power Delivery Design Guidelines For Desktop LGA775 Socket (31321402.pdf, www.intel.com). 16. Voltage Regulator-Down (VRD) 10.1 Design Guide For Desktop LGA775 Socket (30235604.pdf, www.intel.com). 17. Specialty Polymer Aluminum Electrolytic Capacitors. TECHNICAL GUIDE. Panasonic Industrial Company (SP-Cap_2004-technical-guide.pdf, www.panasonic.com). 18. 370-Pin Socket (PGA370) Design Guidelines (24441002.pdf, www.intel.com). 19. Intel® Pentium® 4 Processor 478-Pin Socket (mPGA478) Design Guidelines (24989002.pdf, www.intel.com). 20. Intel® Pentium® 4 Processor with 512-KB L2 Cache on 0.13 Micron Process Datasheet (29864310.pdf, www.intel.com). 21. LGA775 Socket Mechanical Design Guide (30266603.pdf, www.intel.com). 22. Intel® Pentium® 4 Processor 6xx Sequence and Intel® Pentium® 4 Processor Extreme Edition Datasheet (30638203.pdf, www.intel.com). 23. Intel Pentium 4 Processor VR-Down Design Guidelines (24989104.pdf, www.intel.com).
24.06.2006. (с) Ярослав Малов, иначе известный как Ter_Abit.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Чем конденсатор больше не является
Одно из общераспространенных мнений состоит в том, что основная роль конденсатора заключается в хранении заряда, подобно тому, как ведро с водой наполняется одной чашкой и в то же время опустошается другой.
Если вы когда-либо вступали в дискуссию “протекает ли ток через конденсатор” и уходили больше в политику, чем в физику, вы знаете, что типовые аналогии не имеют особого смысла, когда речь идет о переменном токе. Конденсатор – это просто два проводника, разделенных диэлектриком, и нигде в основных физических объяснениях его свойств вы не найдете объяснения того, что с этим делать.
Хранение энергии – это лишь одно из множества применений конденсатора, таких как фильтрация, формирование и инвертирование электрических сигналов и импедансов. Мы привыкли думать, что это основное применение конденсатора, поскольку это было его первым применением на заре электричества постоянного тока и электроскопа Уильяма Гилберта, изобретенного в XV веке.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
- µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Будет интересно➡ Виды источников тока
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
- l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Как устроен конденсатор?
Вообще говоря, конденсатор накапливает на обкладках заряд (множество элементарных частиц, каждая из которых обладает элементарным зарядом). Чем больший заряд накоплен, тем большая запасена энергия. Ёмкость конденсатора зависит также и от вида диэлектрика.
Две пластины, разделенные тонким воздушным слоем (воздух — тоже диэлектрик), обладают очень небольшой емкостью, и в таком виде конденсаторы не используются.
С помощью специальных материалов и технологических ухищрений научились достаточно большую ёмкость втискивать в очень небольшой объём.
Самый характерный пример — электролитические конденсаторы.
В них две металлические обкладки в виде длинных полос (чаще всего из алюминиевой фольги) разделены слоем бумаги, пропитанной электролитом.
Электролит вызывает образование тонкой пленки оксида (окисла), которая является хорошим диэлектриком.
Поэтому электролитические конденсаторы называют ещё оксидными. Полосы сворачивают и помещают в цилиндрический алюминиевый корпус.
Раньше выводы конденсаторов делали из меди – как из материала с высокой электропроводностью. Теперь же их нередко делают из более дешевых сплавов на основе железа. В этом можно убедиться, если поднести к ним магнит. Фирмачи научились экономить!
В керамических конденсаторах диэлектриком служит пластинка из керамики, а обкладками – напыленные на керамику пленки металлических сплавов.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Любопытно, что…
…немецкий каноник фон Клейст, независимо от голландского профессора Мушенбрука проведший опыт с лейденской банкой и испытавший ее разряд, пытался, по-видимому, использовать ее для получения электризованной воды, считавшейся полезной для здоровья.
…в 1827 году французский ученый Савар обнаружил, что после разряда лейденской банки через проволоку, намотанную на железную спицу, последняя часто оказывалась намагниченной. Удивительным же было то, что на одном и том же конце спицы появлялся иногда северный, а иногда южный полюс, хотя банка все время заряжалась одинаково. Объяснение пришло позже — вместе с пониманием колебательного характера разряда.
…Герц не только не помышлял о радиосвязи, но даже отрицал ее возможность.
…проблему передачи сигналов на расстояния пытался решить своим, отличным от Попова и Маркони, путем и Резерфорд. Однако, узнав в 1897 году о результатах Маркони, Резерфорд прекратил дальнейшие опыты в этой области и переключился на исследования радиоактивности.
…новый метод получения импульсных сверхсильных магнитных полей Капица предложил во время работы в Кавендишской лаборатории. Вот как описывал работу его установок знаменитый американский математик Норберт Винер: «…мощные генераторы… замыкались накоротко, создавая токи огромной силы, пропускавшиеся по массивным проводам; провода шипели и трещали, как рассерженные змеи, а в окружающем пространстве возникало магнитное поле колоссальной силы».
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Как они проводят переменный ток
Чтобы убедиться в этом воочию, достаточно собрать несложную схему. Сначала надо включить лампу через конденсаторы C1 и C2, соединенные параллельно. Лампа будет светиться, но не очень ярко. Если теперь добавить еще конденсатор C3, то свечение лампы заметно увеличится, что говорит о том, что конденсаторы оказывают сопротивлению прохождению переменного тока. Причем, параллельное соединение, т.е. увеличение емкости, это сопротивление снижает.
Отсюда вывод: чем больше емкость, тем меньше сопротивление конденсатора прохождению переменного тока. Это сопротивление называется емкостным и в формулах обозначается как Xc. Еще Xc зависит от частоты тока, чем она выше, тем меньше Xc. Об этом будет сказано несколько позже.
Другой опыт можно проделать используя счетчик электроэнергии, предварительно отключив все потребители. Для этого надо соединить параллельно три конденсатора по 1мкФ и просто включить их в розетку. Конечно, при этом надо быть предельно осторожным, или даже припаять к конденсаторам стандартную штепсельную вилку. Рабочее напряжение конденсаторов должно быть не менее 400В.
После этого подключения достаточно просто понаблюдать за счетчиком, чтобы убедиться, что он стоит на месте, хотя по расчетам такой конденсатор эквивалентен по сопротивлению лампе накаливания мощностью около 50Вт.