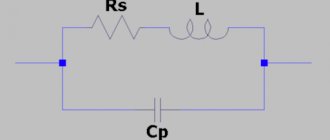
Индуктивность: формула. Измерение индуктивности. Индуктивность контура

Индуктивность контура — теоретические основы

Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.

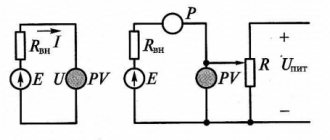
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:

Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.

По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током катушки L=Ψ/i.

Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.

Поток сцепления катушки индуктивности равен Ψ=L×i.

В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.

Напряжение на индуктивности уравновешивает ЭДС и может быть записано в виде uL=-eL=dΨ/dt=L×di/dt.

Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.

Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.

Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.

Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.

Введение

Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.

При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.

Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio

— наведение, побуждение — и обозначают совершенно разные понятия.

Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.

Определение индуктивности

В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:

или

Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.

При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:

Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:

То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.

Проведём исследование поведения тока в индуктивности:

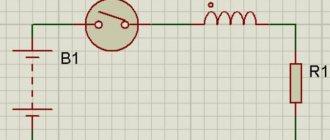
Рис. 1. Электрическая схема эксперимента

Рис. 2. Физическая реализация эксперимента

Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.

Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.

Проведём исследование напряжения на катушке индуктивности:

Рис. 4. Электрическая схема эксперимента

Рис. 6. Осциллограмма напряжения на индуктивности (голубая)

В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.

Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.

Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.

Вот что показали эти опыты:

1. Индукционный ток возникает только при изменении линий магнитной индукции.

1. Направление тока различается при увеличении числа линий и при их уменьшении.

1. Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Соленоид

Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:

• df : dt = L dl : dt.

Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.

В наше время устройство может соединять в себе гидравлику и электронику. На этой основе созданы четыре модели:

• Первая способна контролировать линейное давление.
• Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
• Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
• Четвертая управляется гидравлическим способом или клапанами.

Как найти индуктивность контура

Формула, которая является простейшей для нахождения величины, следующая:

• L = F : I,

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

• Ei = -L х dI : dt.

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

• W = L I2 : 2.

Индуктивность, ее единица си. Индуктивность длинного соленоида.

Индукти́вность

(или
коэффициент самоиндукции
) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность , краем которой является этот контур. .

—магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока :

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током :

.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

• L= µ0n2V,

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

• L = µ0N2S : l,

Будет интересно➡ Электротехника для чайников. Как научиться разбираться в электрике: уроки для начинающих

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

• B= µ0nI,

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

• E = LI2 :2,

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Обозначение и единицы измерения

Сопротивление тока: формула

В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Джозеф Генри

Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.

Как может обозначаться индуктивность в других системах:

• В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
• В системе СГСЭ – в статгенри.

Свойства

Имеет следующие свойства:

• Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
• Не может быть отрицательной;
• Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
• При увеличении частоты тока реактивное сопротивление катушки увеличивается;
• Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

• Ce = C : (1 – 4Π2f2LC),

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

• Lk = Lp + Lm + Lb,

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

• Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.

Колебательные контуры

Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:

• XL = W х L,

где XL показывает реактивное сопротивление катушки, а W — круговая частота.

Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:

Xc = 1 : W х C.

Важными характеристиками колебательного контура являются резонансная частота, волновое сопротивление и добротность контура. Первая характеризует частоту, где сопротивление контура имеет активный характер. Вторая показывает, как проходит реактивное сопротивление на резонансной частоте между такими величинами, как емкость и индуктивность колебательного контура. Третья характеристика определяет амплитуду и ширину амплитудно-частотных характеристик (АЧХ) резонанса и показывает размеры запаса энергии в контуре по сравнению с потерями энергии за один период колебаний. В технике частотные свойства цепей оцениваются при помощи АЧХ. В этом случае цепь рассматривается как четырехполюсник. При изображении графиков используется значение коэффициента передачи цепи по напряжению (К). Эта величина показывает отношение выходного напряжения к входному. Для цепей, которые не содержат источников энергии и различных усилительных элементов, значение коэффициента не больше единицы. Оно стремится к нулю, когда на частотах, отличающихся от резонансной, сопротивление контура имеет высокое значение. Если же величина сопротивления минимальна, то коэффициент близок к единице.

При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:

• Q = R√C : L.

При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.

“Катушка ниток”

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

• I = U : R,

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

1. С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
2. С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

• L = 10µ0ΠN2R2 : 9R + 10l.

А вот уже для многослойной другая формула:

• L= µ0N2R2 :2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

1. На цилиндрическом феррите самая большая индуктивность возникает в середине.
2. Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
3. Индуктивность тем меньше, чем меньше количество витков.
4. В тороидальном сердечнике расстояние между витками не играет роли катушки.
5. Значение индуктивности зависит от “витков в квадрате”.
6. Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
7. При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Будет интересно➡ Что такое реактивная мощность и как её рассчитать?

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Вариометр

Что такое катушка, показано выше на простых примерах. На практике для обозначения однотипных групп применяют специфическую терминологию. Вариометром, например, называют деталь с переменной индуктивностью. В типовой конструкции применяют две катушки, установленные одна внутри другой. Необходимый результат получают регулировкой взаимного положения функциональных компонентов. Для перемещения применяют ручной привод или автоматизированный механизм с внешней схемой управления.

К сведению. Не следует путать определения. Мультипликаторная катушка, например, – это приспособление для рыбной ловли. Такое устройство будет обладать индуктивностью при наматывании лески из проводящего материала. Однако в радиотехнических схемах подобные устройства не используют.

Мультипликаторные катушки

Особенности других конструкций:

• Дроссель обеспечивает высокое сопротивление цепи переменному току, поэтому такой пассивный индуктивный элемент часто применяют для создания фильтров. При подключении к сети питания 220В/ 50 Гц используют железные сердечники. При повышении частоты – ферритовые аналоги.
• Контурные катушки магнитные устанавливают в комбинации с конденсаторами для создания схем с определенной полосой пропускания.
• Электрическим реактором называют крупные конструкции, которые применяют в силовых сетях.
• Сдвоенные катушки применяют для разделения цепей по постоянной составляющей.

Токовый реактор ограничивает сильный ток, предотвращает развитие аварийной ситуации при КЗ

Выше отмечены типовые области применения элементов с индуктивными характеристиками. Они пригодны для создания фильтров, ограничения тока и разделения цепи прохождения постоянных и переменных составляющих сигнала. Магнитное поле катушки с током распространяется в пространстве. Чтобы предотвратить паразитное воздействие, отдельные компоненты размещают на достаточном расстоянии.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Будет интересно➡ Способы подключения асинхронного электродвигателя

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Об индуктивности простыми словами

Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).

Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.

Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.

Ɛ=- L(dI/dt), где:

• Ɛ – ЭДС самоиндукции;
• L-индуктивность;
• I – сила тока;
• t – время.

При этом L равно магнитному полю (Ф) деленному на силу тока (I).

Самоиндукция

Индуктивность: формула

Если через замкнутый контур пропускать переменный ток, можно зарегистрировать с помощью простых экспериментов магнитное поле в окружающей среде. Изменение силовых параметров сопровождается появлением в цепи наведенной электродвижущей силы. Данное явление называют самоиндукцией.

Величину ЭДС можно вычислить по формуле:

Е = -L * (Δi/Δt).

Это выражение показывает зависимость напряжения от изменения тока за единицу времени. Поправочный коэффициент (L) обозначает особенности проводника (индукционной катушки). Знак «-» характеризует инерционные свойства явления.

При пропускании синусоидального сигнала следует учитывать отставание напряжения (векторное выражение) от тока на 90 градусов. Амплитуда будет прямо пропорциональна частоте (w):

E = L * I * w.