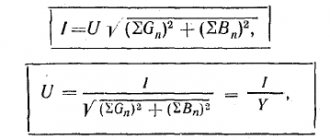| Значение напряжения(комплексное выражение или через пробел амплитуда и фаза) |
| Значение тока(комплексное выражение или через пробел амплитуда и фаза) |
| Значение сопротивления(комплексное выражение или через пробел амплитуда и фаза) |
| Мгновенное значение напряжения |
| Действующее значение напряжение |
| Комплексное значение напряжения |
| Мгновенное значение тока |
| Действующее значение тока |
| Комплексное значение тока |
| Комплексное значение сопротивления |
| Комплексное значение проводимости |
| Угол сдвига фаз между напряжением и тока |
| Активная составляющая напряжения |
| Реактивная составляющая напряжения |
| Активная составляющая тока |
| Реактивная составляющая тока |
В помощь тем, кто начал изучать электротехнику и иногда путается в расчетах комплексных токов и напряжений, и создан этот калькулятор.
Напомним, что мгновенное значения переменного тока может быть выражено в виде гармонического колебания
где — какой либо момент времени
— угловая частота
— начальная фаза
Таким же способом можно представить и мгновенное значения напряжения
Если мы попытаемся оценить какой же среднее значение тока будет за какой то определенный период, мы столкнемся с определенными трудностями.
Так как мгновенный ток за период может принимать как положительные так и отрицательные значения, то сложив их, мы получим что среднее значения тока равно нулю. Но такого быть не может…
Ток прошедший за этот период, сделал же какую то работу, он же не мог исчезнуть без ничего, не оставив следов.
Какую же работу может сделать ток прошедший через проводник? Самый простой и ощущаемый процесс это нагревание проводника. А по закону Джоуля-Ленца, который определяет сколько же электрической энергии уходит в тепловую, есть связь между нагревом(выделением теплоты) и проходящим через проводник значением тока.
Таким образом экспериментально, а потом уже и теоретически определили, что между амплитудой тока и «средним» значением ( правильно его назвать действующим ) есть простое соотношение.
Именно действующее значении тока, выполняет работу и участвует в вычислениях мощности. Именно это значение показывает вольтметр когда мы измеряем напряжение переменного тока.
Такие же рассуждения насчет напряжения приводят нас к подобной формуле.
Мы также гармоническое колебание можем представить в комплексном виде ( показательной форме )
Это не наша прихоть. Это лишь желание упростить вычисления которые встречаются в электротехнике.
Например при сложении двух периодически изменяющихся значений тока, лучше использовать векторное сложение. А что такое векторное сложение, как не работа с комплексными числами? И так во всем в электротехнике.
Поэтому мы можем значение действительного тока выразить вот так
Тогда, зная комплексные значения тока или напряжения в виде ,мы можем узнать модуль действительной величины тока , а также начальную фазу
Общая электротехника (стр. 25 )
В электрических цепях несинусоидальный ток может присутствовать в двух случаях:
· при действии источников несинусоидального напряжения или тока;
· вследствие нелинейности элементов электрической цепи.
1. Способы представления несинусоидальных функций
При расчете цепей несинусоидального переменного тока используется разложение периодических функций в одну из форм гармонического ряда Фурье. Если функция с периодом T
представлена суммой
мгновенных значений гармонических колебаний
различных частот , где
k
=1, 2, ¼ порядковый номер гармоники, то ряд Фурье записывают в следующем виде
где – постоянная составляющая функции , равная ее среднему за период Т
значению;
и – коэффициенты ряда Фурье, соответствующие амплитудам гармоник квадратурных составляющих;
– амплитуда
k
-ой гармоники;
– начальная фаза
k
-ой гармоники.
Зависимости и от порядкового номера k
-ой гармоники (или от ее частоты ) принято называть амплитудным и фазовыми спектрами колебания соответственно. Для периодических несинусоидальных колебаний амплитудный и фазовые спектры имеют дискретный характер, а расстояние по оси частот между смежными спектральными линиями равно . Теоретически ряд Фурье содержит бесконечное число членов, однако в большинстве практических случаев этот ряд достаточно быстро сходится, и при расчетах можно ограничиться сравнительно небольшим числом гармоник.
2. Энергетические характеристики несинусоидального тока
При расчете энергетических характеристик в цепях несинусоидального периодического тока используют следующие величины:
· действующие значения напряжения U
и тока
I
;
· среднюю мощность Р
;
· реактивную Q
и полную
S
мощности, а также
· мощность искажений D
, коэффициент искажений и мощности ,;
Действующие значения напряжения и тока
определяют как геометрическую сумму действующих значений отдельных гармоник
где –
действующее значение
k
-ой гармоники напряжения;
–
действующее значение
k
-ой гармоники тока;
–
постоянные составляющие напряжения и тока, соответственно.
Среднюю мощность
несинусоидального тока определяют как сумму мощностей отдельных гармоник
,
где – средняя мощность k
-ой гармоники тока;
– мощность постоянного тока.
Полную мощность
несинусоидального тока определяют аналогично полной мощности синусоидального тока по формуле
S=UI.
По аналогии с синусоидальным током вводится понятие реактивной мощности
,
где – реактивная мощность k
-ой гармоники тока;
В отличие от синусоидального тока полная мощность S
оказывается больше геометрической суммы средней и реактивной мощностей
3. Расчет цепей несинусоидального переменного тока
При негармонических воздействиях алгоритм расчета цепи может быть следующим:
1) периодическое негармоническое воздействие представляют в виде суммы гармонических сигналов
, используя ряд Фурье;
2) ограничивают бесконечный ряд Фурье некоторым числом гармоник
, учитывая при этом, что мощность каждой последующей гармоники убывает пропорционально квадрату ее амплитуды;
3) выполняют расчет цепи для каждой отдельной гармоники напряжения или тока, учитывая при этом, что структура цепи сохраняется, а сопротивления и проводимости реактивных элементов изменяются
с изменением частоты гармоники;
4) результирующую реакцию цепи находят при помощи метода наложения путем сложения реакций для отдельных гармоник воздействия.
В табл. 1. приведены некоторые типовые функции и их разложения в ряд Фурье. Графики этих функций приведены на рис. 4.1. При этом приняты следующие обозначения: .
Таблица 4.1. Ряды Фурье для несинусоидальных функций рис. 4.1. *
| № графика функции. | Разложение функции в ряд Фурье |
| 1 | 2 |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 1 | 2 |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 1 | 2 |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 |
Следует помнить, что для расчетов данные функции нужно привести к виду:
Приведение осуществляется следующим образом:
ЗАДАЧА 4
Дано:
К электрической цепи, схема которой приводится ниже, приложено несинусоидальное периодическое напряжение, форма которого также показана. Параметры цепи имеют следующие значения: [Ом]; [Гн]; [мкФ]; [В]; [рад/с].
Требуется выполнить следующие операции:
1) представить напряжение источника f
(
x
)=
e
(w
t
) рядом Фурье, ограничив число членов ряда постоянной составляющей и тремя первыми гармониками.
2) построить графики спектров амплитуд и начальных фаз заданного источника.
3) определить напряжение на нагрузке , используя метод расчета по комплексным значениям;
4) построить графики спектральных составляющих для напряжения (тока) на нагрузке.
5) определить действующее значение напряжения (тока) на нагрузке и мощность, рассеиваемую в ней.
| а ) Схема цепи (а ) и форма входного напряжения ( |
Решение
1.
Воспользуемся данными табл. 1 (функция ) и представим напряжение источника в виде ряда Фурье, ограниченного постоянной составляющей и тремя первыми гармониками
2.
Построим графики спектров амплитуд и начальных фаз напряжения источника, которые изображены на рис. 4.3
а
,
б
. При построении графиков используем масштаб, при котором одно деление по оси ординат соответствует 10 В, а по оси абсцисс – 100 Гц.
| а ) Рис. 4.3. Спектры амплитуд (а ) и фаз ( |
3.
Теперь выполним расчет напряжения на нагрузке, используя для этого метод комплексных амплитуд.
Для постоянной составляющей
напряжения на нагрузке, используя схему замещения, приведенную на рис. 4.4
а
, получим следующее значение
[В].
При выполнении этого расчета учтено, что на постоянном токе индуктивности , нужно заменить перемычками, а емкость – разрывом цепи, как показано ниже на рисунке. Ток в нагрузке определим по закону Ома
[А].
При расчете напряжения на нагрузке для гармоник ЭДС e
(
t
) источника можно пользоваться схемой замещения, приведенной на рис 4.4
б.
На этой схеме все элементы цепи заменены их комплексными сопротивлениями, которые имеют двойные индексы. Первый индекс соответствует порядковому номеру ветви, а второй – номеру гармоники. Комплексные значения токов в ветвях определим по формулам
где – эквивалентное комплексное сопротивление цепи для k
-ой гармоники напряжения источника;
в которых учтено, что ток делится в ветвях схемы на два тока, которые обратно пропорциональны сопротивлениям ветвей.
| а ) ) и переменных ( |
Для первой гармоники,
пользуясь схемой замещения, получим напряжения на нагрузке
[В]; [Ом]; [Ом]; [Ом] – сопротивления цепи для первой гармоники напряжения источника.
Комплексная амплитуда тока первой гармоники источника имеет значение
[А]
Этот ток делится обратно пропорционально сопротивлениям параллельно включенных ветвей и , поэтому ток в нагрузке
[А]
Комплексное значение напряжения на нагрузке определим по закону Ома
[В]
Полученное значение позволяет записать мгновенное значение первой гармоники напряжения на нагрузке
[В]
Вторую гармонику
напряжения на нагрузке определим, используя в схеме замещения рис. 4.4
б
сопротивления цепи и напряжение источника для второй гармоники
[В]; [Ом]; [Ом]; [Ом].
Значение комплексной амплитуды тока второй гармоники в цепи источника напряжения найдем по закону Ома
[А]
Комплексную амплитуду тока второй гармоники в нагрузке R
н найдем аналогично току первой гармоники путем деления тока источника обратно пропорционально сопротивлениям параллельно включенных ветвей
[А]
Комплексное значение напряжения второй гармоники на нагрузке найдем с помощью закона Ома
[В]
Полученное значение позволяет записать мгновенное значение второй гармоники напряжения на нагрузке
[В]
Определение напряжения четвертой гармоники
выполним аналогично расчету напряжения второй гармоники. Сопротивления цепи и напряжение источника для четвертой гармоники имеют значения
В; [Ом]; [Ом]; [Ом].
Комплексную амплитуду тока четвертой гармоники определим по закону Ома
[А]
Используя ток четвертой гармоники в ветви с источником напряжения, рассчитаем ток в нагрузке
[А]
Комплексное значение четвертой гармоники напряжения на нагрузке определим по закону Ома
[В]
Мгновенное значение второй гармоники напряжения на нагрузке определим по формуле
[В]
Результирующее напряжение на нагрузке найдем путем суммирования отдельных составляющих, рассчитанных выше
Представим графики ЭДС источника e
(
t
) и напряжения нагрузки
4.
Построим графики спектральных составляющих напряжения на нагрузке, используя полученное выше мгновенное значение напряжения. Эти графики показывают, что электрическая цепь, включенная между источником и нагрузкой, оказывает определенное сглаживающее действие: амплитуды спектральных составляющих уменьшаются по мере увеличения частоты. Кроме этого, заметно существенное запаздывание сигнала по отношению к напряжению источника.
5.
Определим действующее значение напряжения на нагрузке и среднюю мощность, рассеиваемую в ней. Действующее напряжение на нагрузке можно рассчитать по формуле:
где =31,80 В – постоянная составляющая напряжения на нагрузке;
В – действующее значение напряжения первой гармоники;
В – действующее значение напряжения второй гармоники;
В – действующее значение напряжения четвертой гармоники.
Средняя мощность несинусоидального тока определяется по формуле:
где Вт – мощность постоянной составляющей тока;
Вт – средняя мощность первой гармоники тока;
Вт – средняя мощность второй гармоники тока;
Вт – средняя мощность четвертой гармоники тока.
Из полученных выражений следует, что средняя мощность почти полностью определяется постоянной составляющей и первой гармоникой тока. Вклад высших гармоник весьма незначителен и составляет всего 1,6% от полной мощности, рассеиваемой в нагрузке.
ЗАДАНИЕ 4
Для заданной схемы электрической цепи, структура которой представлена на рис 1 или 2 и параметрами из таблиц 4.1…4.4, выполнить:
1) представить заданную функцию источника ЭДС или тока рядом Фурье, ограничив число членов ряда постоянной составляющей и тремя первыми гармониками.
2) построить графики спектров амплитуд и начальных фаз заданного источника.
3) определить функцию — напряжение или ток на нагрузке, используя метод расчета по комплексным значениям;
4) построить графики спектральных составляющих для напряжения (тока) на нагрузке.
5) определить действующее значение напряжения (тока) на нагрузке и мощность, рассеиваемую на нагрузке.
Рис.1 Рис.2
Перед расчетом в соответствии с вариантом задания необходимо составить электрическую схему цепи, заменив элементы структуры элементами R,
L
и
C
. В качестве примера составим схему варианта 29 таблицы 4.1
| Из за большого объема этот материал размещен на нескольких страницах: 25 |
Получить текст
Основы комплексного расчета электрических цепей
Определение 1
Комплексный ток — это комплексное действующее значение синусоидального тока.
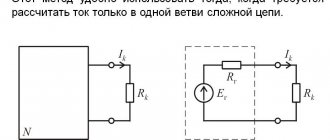
Одним из основных способов расчета электрических цепей переменного тока является символический или комплексный метод. Как правило, он используется при анализе электрических схем с гармоническими токами, напряжениями и электродвижущей силой. В результате решения получается комплексное значение напряжений и токов. Синусоидальная величина может быть представлена:
- В форме вращающегося вектора.
- В виде комплексного числа.
Пример вращающегося вектора изображен на рисунке ниже.
Рисунок 1. Пример вращающегося вектора. Автор24 — интернет-биржа студенческих работ
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
По данному рисунку видно, что синусоидальная величина а изменяется с течением времени, которая может быть входным напряжением или любым другим параметром электрической сети. Величина имеет некоторое начальное значение (t=0) при начальной фазе ф:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
При угле Wt3, когда сумма Wt3+ф=90 и соответственно:
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Курсовая работа Комплексный расчет электрических сетей 480 ₽ Реферат Комплексный расчет электрических сетей 220 ₽ Контрольная работа Комплексный расчет электрических сетей 220 ₽
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Синусоидальная величина при угле Wt7, когда сумма Wt7 + ф = 270 будет иметь отрицательное значение:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
Величина будет иметь отрицательное значение при углах Wtn + ф = 0, когда Wtn = –ф (данная область на рисунке не отмечена), таким образом:
Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ
Также нулевое значение у синусоидальной величины будет при угле Wt11, когда Wt11+ ф = 360:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Именно по такому закону может меняться синусоидальная величина, например напряжение, изменяясь от 0 до максимального значения и обратно.
Другая форма представления — комплексная
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Для этого строится график (комплексная плоскость) зависимости двух величин, как на рисунке ниже.
Рисунок 8. График. Автор24 — интернет-биржа студенческих работ
Длина вектора Аm равна максимальному значению амплитуды рассматриваемой величины. Если учитывать начальную фазу (ф), то это число записывается следующим образом.
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
В практических расчетах комплексного метода применяют не амплитудное значение, а действующее, которое меньше в корень из 2 амплитудного:
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
При работе с комплексными числами применяется один из трех способов записи комплексного числа: тригонометрическая форма, алгебраическая форма, показательная форма. Например, имеется комплексное число в показательной форме:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
В тригонометрической форме оно будет иметь следующий вид:
Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ
В итоге при переходе в алгебраическую форму, учитывая, что:
Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ
получаем:
Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ
где, ReA = 8,66 – действительная составляющая комплексного числа; ImA = 5 – мнимая составляющая комплексного числа.
При переходе от алгебраической формы к показательной получаем число следующего вида
Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ
Оно переходит к показательной форме следующим преобразованием:
Рисунок 16. Формула. Автор24 — интернет-биржа студенческих работ
А угол рассчитывается по формуле
Рисунок 17. Формула. Автор24 — интернет-биржа студенческих работ
И в итоге получается:
Рисунок 18. Формула. Автор24 — интернет-биржа студенческих работ
Комплекс действующего значения
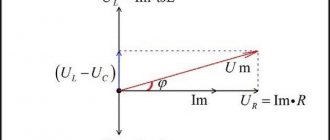
Изображение синусоидальных токов и напряжений с помощью векторов на комплексной плоскости. Комплексная амплитуда.
Комплекс действующего значения
Мы уже изображали токи и напряжения в виде векторов, остается лишь взять комплексную плоскость:
В отличие от математики, мнимая единица обозначается буквой , т.к. обозначает мгновенное значение тока.
Длина комплексного вектора равна амплитудному или действующему значению. В первом случае её называют комплексной амплитудой
, во втором –
комплексом действующего значения
. Угол поворота соответствует фазе .
Как известно из математики, комплексные числа имеют две основные формы записи: алгебраическая и показательная (экспоненциальная). Есть ещё тригонометрическая форма, но она является как бы переходом от показательной к алгебраической, поэтому ей не уделяют внимание.
– это комплексная амплитуда в показательной форме записи.
Это не простое комплексное число, это временная функция, поэтому, для того, чтобы отличить её от простых комплексных чисел, которые обозначают подчёркиванием, комплексную амплитуду обозначают точкой вверху.
Чтобы получить комплекс действующего значения, нужно комплексную амплитуду поделить на :
Это тоже комплексная функция времени, поэтому обозначается точкой вверху.
Аналогично токам вводятся комплексные амплитуды и комплексы действующих значений напряжений.
Для того чтобы перейти от комплексов к мгновенным значениям, нужно взять проекции комплексной амплитуды на мнимую ось:
Вектор комплексной амплитуды, также как вектор комплекса действующего значения, вращается на комплексной плоскости с угловой частотой (циклической частотой) . Работать с такими векторами невозможно. Чтобы остановить этот вектор, берут время = 0: ; тогда
Переход от показательной формы к алгебраической осуществляется через тригонометрическую форму. Необходимо взять проекции комплексного вектора на действующую ось – , и на мнимую ось .
(формула Эйлера)
Для перехода от алгебраической формы к экспоненциальной используется следующая формула:
Внимание!!! Эта формула работает, если вектор находится в I или IV четверти комплексной плоскости, т.е. когда , если (вектор находится во II или III четверти), тогда нужно пользоваться другой формулой:
т.е. умножение комплексного вектора на эквивалентно его повороту на комплексной плоскости на раз, а умножение на –
эквивалентно повороту на раз.
Итак,
Выводы:
Синусоидальным периодическим функциям токов и напряжений можно поставить в соответствие временные функции на комплексной плоскости, которые называются изображениями и несут всю информацию о реальных функциях (токов и напряжений), об их амплитудах и фазах, поэтому для комплексных функций выполняются законы Кирхгофа. Сложение, вычитание, деление, умножение, дифференцирование и интегрирование реальных функций можно заменить на те же операции с комплексными изображениями.
| | | следующая лекция ==> | |
| треугольники напряжений, сопротивлений, мощностей | | | Комплексные напряжения (на сопротивлениях, индуктивностях и ёмкостях). Комплексные сопротивления. Законы Ома в комплексной форме |
Дата добавления: 2016-05-28; просмотров: 6615; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Узнать еще:
Приложение комплексных чисел в электротехнике
Первое упоминание о «мнимых» числах как о квадратных корнях из отрицательных чисел относится еще к XVI веку. Итальянский ученый Джироламо Кардано (1501-1576) в 1545 году опубликовал работу, в которой, пытаясь решить уравнение
, он пришел к выражению
. Через это выражение представлялись действительные корни уравнения:
Таким образом, в работе Кардано мнимые числа появились как промежуточные члены в вычислениях. Заслуга Кардано состояла в том, что он допустил существование «несуществующего» числа
, введя правило умножения: все остальное стало делом техники.
Однако еще три столетия математики привыкали к этим новым «мнимым» числам, время от времени пытаясь от них избавиться. Только с XIX века, после выхода в свет работ Карла Фридриха Гаусса (1777-1855), посвященных доказательству основной теоремы алгебры, комплексные числа прижились в науке.
Комплексные числа – один из наиболее подходящих разделов курса математического анализа для реализации профессиональной направленности бакалавров по направлению подготовки Информатика и вычислительная техника. При изучении комплексных чисел необходимо учитывать применение математических знаний в общетехнических и специальных дисциплинах, в частности электротехнике. Применение комплексных чисел дает возможность использовать законы, формулы и методы расчетов, применяющиеся в цепях постоянного тока, для расчета цепей переменного тока, упростить некоторые расчеты, заменив графическое решение с использованием векторов алгебраическим решением, рассчитывать сложные цепи, которые другим путем решить нельзя, упростить расчеты цепей постоянного и переменного токов.
При расчетах цепей приходится проводить математические операции с комплексными числами, поэтому студенты должны уметь выполнять следующие операции: 1) находить модуль и аргумент комплексного числа и комплексное число по модулю и аргументу; 2) переводить комплексное число из одной формы в другую; 3) производить сложение и вычитание, умножение и деление комплексных чисел.
Помимо этого, очень важно научить строить кривую и вектор по уравнению синусоиды, вектор по комплексному числу, определять комплексное число по вектору и уравнению, уравнение по комплексному числу.
В электротехнике тема «Переменный ток» занимает значительное место. Это объясняется тем, что большинство электротехнических установок работает на переменном токе, который изменяется синусоидально.
Уравнение переменного напряжения имеет вид , где u – мгновенное значение напряжения;
–максимальное значение (амплитуда) напряжения; w
– угловая частота
;t
– время
;
– начальный фазовый угол
;
– электрический угол
.
Это уравнение связывает две переменные величины: напряжение
u
и время
t
. С течением времени напряжение изменяется синусоидально.
Аналогичный вид имеют уравнения и других синусоидально изменяющихся величин: тока , э.д.с.
и т.д.
При расчете цепей переменного тока приходится использовать синусоидально изменяющиеся величины, т.е. производить сложение, вычитание, умножение и деление уравнений указанного выше типа.
Сложение синусоидальных величин трудоемко, особенно если приходится складывать большое число уравнений. Синусоидальная величина однозначно представлена вращающимся вектором, длина которого равна амплитуде, а начальное положение определяется углом
, вращение вектора происходит с угловой скоростью w
. Операции производятся с уравнениями, имеющими одинаковую угловую частоту, то есть все векторы, заменяющие уравнения, вращаются с одинаковой угловой скоростью. Следовательно, их взаимное расположение не меняется, отпадает необходимость вращения векторов. Так как векторы заменяют синусоидальные величины, то сложение или вычитание, возможно, заменить сложением или вычитанием векторов.
Переменная синусоидальная величина обладает свойствами:
1. Переменная синусоидальная величина может быть однозначно представлена вектором. Длина вектора равна амплитуде; угол наклона равен начальному фазовому углу.
2. Сложение (и вычитание) синусоидальных величин можно заменить сложением (и вычитанием) векторов.
Кроме сложения и вычитания синусоидальные величины приходится умножать и делить. И здесь на помощь приходят комплексные числа.
Комплексное число может быть изображено на плоскости вектором, длина которого равна модулю комплексного числа, а угол наклона – аргументу. В электротехнике в отличие от математики мнимая единица обозначается буквой j
. Если имеется комплексное число
A=a+jb,
то его можно представить вектором, где
– модуль комплексного числа;
– аргумент комплексного числа.
Комплексное число имеет три формы: алгебраическую – A=a+jb;
тригонометрическую –
; показательную –
.
Комплексное число однозначно представлено вектором, а определенному вектору соответствует определенное комплексное число.
Таким образом, если переменная синусоидальная величина может быть представлена вектором, а определенному вектору соответствует определенное комплексное число, то переменная синусоидальная величина может быть представлена комплексным числом.
Такие величины как: напряжение и ток, сопротивление и проводимость, мощность выражаются комплексными числами.
Напряжение и ток.
Имеется уравнение
. В электротехнике за длину вектора берется не максимальное, а действующее значение. Оно обозначается большой буквой
U
без индекса и вычисляется путем деления максимального значения на
.
Синусоидальная величина, выраженная комплексным числом, называется комплексом
и обозначается прописной буквой с точкой наверху . Комплекс напряжения можно написать в трех формах алгебраической – , тригонометрической –
и показательной –
.
Таким образом, в комплексе напряжения модуль равен действующему значению, аргумент – начальному фазовому углу, активная составляющая – вещественной части комплекса напряжения, реактивная – мнимой части.
Аналогично для тока: ,
, , ,
.
Пример.
Дано: ток в комплексной форме
Написать уравнение тока.
Решение.
Для того чтобы написать уравнение, надо знать амплитуду и начальный фазовый угол. Поэтому надо найти модуль – действующее значение и аргумент – начальный фазовый угол заданного комплекса тока:
,
,
,
.
Сопротивление и проводимость.
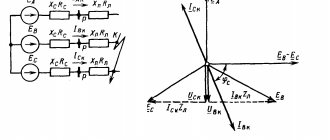
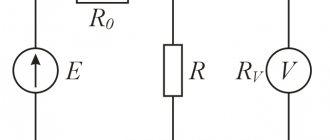
Имеется цепь (рис. 1):
r
– активное сопротивление (лампа накаливания);
– индуктивное сопротивление (катушка);
z
– общее сопротивление цепи, называемое полным.
Рис.1 Рис.2
Сопротивления r, ,
z
образуют прямоугольный треугольник сопротивления (рис. 2). Угол
– угол сдвига фаз. Сопротивления не являются синусоидальными величинами, однако отрезок
z
может быть выражен комплексным числом, считая, что отрезок
r
откладывается по оси вещественных чисел, а отрезок – по оси мнимых чисел.
Сопротивление в комплексной форме обозначается буквой Z
. Для цепи на рис.2 комплекс сопротивления записывается:
– алгебраическая форма;
– тригонометрическая форма; – показательная форма.
Модуль ; аргумент
. Таким образом, в комплексе сопротивления модуль равен полному сопротивлению, а аргумент – сдвигу фаз.
Мощность.
Комплекс мощности получится, если комплекс напряжения умножить на сопряженный комплекс тока: , где
– комплекс мощности, – сопряженный комплекс тока.
После умножения получим комплексное число, у которого вещественная часть равна активной мощности, а мнимая часть – реактивной мощности:
, где P – активная мощность, Q – реактивная мощность.
Пример.
,6; . Определить активную P и реактивную Q мощность.
Решение.
Переведем комплексы напряжения и тока в показательную форму, для этого найдем модуль и аргумент тока и напряжения:
, ,
,
, , .
Определим сопряженный комплекс тока:
,
Найдем активную и реактивную мощности: P=975Вт, Q=171 вар.
Алгебраическая форма комплексного числа удобна при сложении и вычитании, показательная – при умножении и делении; тригонометрическая служит для перевода показательной формы в алгебраическую.
На занятиях преподаватели могут использовать примеры, не вдаваясь углубленно в электротехнику, задания рассматривая их только с математической точки зрения. В качестве дополнительного материала, самостоятельной работы можно предложить задания типа:
- Дано: а) ; б)
; в)
; г)
Найти модуль и аргумент комплексного числа.
- Дано: а)
; б); в)
.
Написать комплексные числа в показательной и алгебраической формах.
- Дано: а)
; б) ; в)
;г) ; д)
; е)
; ж)
.
Перевести алгебраическую форму комплексного числа в показательную и наоборот.
- Выполнить сложение, умножение, деление комплексных чисел.
Дано: а) ; б)
; в)
.
Данная статья поможет преподавателям математики разобраться в вопросе о приложении комплексных чисел в электротехнических расчетах.
Литература:
- Теоретические основы электротехники: Теория электрических цепей и электромагнитного поля: учеб. пособие для студ. высш. учеб. заведений / под ред. С.А. Башарина, В.В. Федорова. – М.: Издательский , 2004. – 304 с.