Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток
— это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.
Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.
Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.
А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости и катушку индуктивности . Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.
Напряжение на клеммах источника меняется по закону:
(1)
Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?
Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным
.
Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.
Текущее значение напряжения в момент времени называется мгновенным значением напряжения
.
Условие квазистационарности
В случае переменного тока возникает один тонкий момент. Предположим, что цепь состоит из нескольких последовательно соединённых элементов.
Если напряжение источника меняется по синусоидальному закону, то сила тока не успевает мгновенно принимать одно и то же значение во всей цепи — на передачу взаимодействий между заряженными частицами вдоль цепи требуется некоторое время.
Между тем, как и в случае постоянного тока, нам хотелось бы считать силу тока одинаковой во всех элементах цепи. К счастью, во многих практически важных случаях мы действительно имеем на это право.
Возьмём, к примеру, переменное напряжение частоты Гц (это промышленный стандарт России и многих других стран). Период колебаний напряжения: с.
Взаимодействие между зарядами передаётся со скоростью света: м/с. За время, равное периоду колебаний, это взаимодействие распространится на расстояние:
м км.
Поэтому в тех случаях, когда длина цепи на несколько порядков меньше данного расстояния, мы можем пренебречь временем распространения взаимодействия и считать, что сила тока мгновенно принимает одно и то же значение во всей цепи.
Теперь рассмотрим общий случай, когда напряжение колеблется с циклической частотой . Период колебаний равен , и за это время взаимодействие между зарядами передаётся на расстояние . Пусть — длина цепи. Мы можем пренебречь временем распространения взаимодействия, если много меньше :
(2)
Неравенство (2) называется условием квазистационарности
. При выполнении этого условия можно считать, что сила тока в цепи мгновенно принимает одно и то же значение во всей цепи. Такой ток называется
квазистационарным
.
В дальнейшем мы подразумеваем, что переменный ток меняется достаточно медленно и его можно считать квазистационарным. Поэтому сила тока во всех последовательно включённых элементах цепи будет принимать одинаковое значение — своё в каждый момент времени. Оно называется мгновенным значением силы тока
.
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
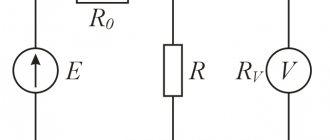
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
Резистор в цепи переменного тока
Простейшая цепь переменного тока получится, если к источнику переменного напряжения подключить обычный резистор (мы полагаем, разумеется, что индуктивность этого резистора пренебрежимо мала, так что эффект самоиндукции можно не принимать во внимание) , называемый также активным сопротивлением
(рис. 1)
Рис. 1. Резистор в цепи переменного тока
Положительное направление обхода цепи выбираем против часовой стрелки, как показано на рисунке. Напомним, что сила тока считается положительной, если ток течёт в положительном направлении; в противном случае сила тока отрицательна.
Оказывается, мгновенные значения силы тока и напряжения связаны формулой, аналогичной закону Ома для постоянного тока:
Таким образом, сила тока в резисторе также меняется по закону синуса:
Амплитуда тока равна отношению амплитуды напряжения к сопротивлению :
Мы видим, что сила тока через резистор и напряжение на нём меняются «синхронно», точнее говоря — синфазно (рис. 2).
Рис. 2. Ток через резистор совпадает по фазе с напряжением
Фаза тока равна фазе напряжения, то есть сдвиг фаз между током и напряжением равен нулю.
Особенности переменного напряжения, тока
Генераторы, вырабатывающие электроэнергию, сконструированы так, что напряжение, скорость изменения заряда в наших линиях электропередач меняются по гармоничному закону:
u = Umsin(ωt+φ0), i = Imsin(ωt+φ0).
Обозначения:
- u, i – мгновенные значения (в произвольный момент времени);
- Um, Im – амплитудные значения (максимальные);
- Um – амплитуда напряжения;
- Im – амплитуда тока;
- t – время;
- величина ω – циклическая частота.
Величина ω связана с линейной частотой ν выражением:
ω = 2πν:
- π = 3,14 – математическая константа;
- ν = 50 Гц (для электрических сетей в нашей стране).
Произведение ωt называют фазой:
ωt = φ.
Измеряют в радианах (рад), φ0 – начальная фаза, зачастую равна нулю. Использование в формулах функции cos не изменяет смысла физических выражений.
Если напряжение, изменяющееся по гармоничному закону, приложить к обычному резистору (в его роли может быть лампа накаливания, тепловой нагреватель), то через него начнут двигаться частицы, характер движения которых изменяется по такому же закону.
Изменение величин будет синхронным, фазы – одинаковыми. Такое сопротивление называют активным.
Конденсатор в цепи переменного тока
Постоянный ток через конденсатор не течёт — для постоянного тока конденсатор является разрывом цепи. Однако переменному току конденсатор не помеха! Протекание переменного тока через конденсатор обеспечивается периодическим изменением заряда на его пластинах.
Рассмотрим конденсатор ёмкости , подключённый к источнику синусоидального напряжения (рис. 3). Активное сопротивление проводов, как всегда, считаем равным нулю. Положительное направление обхода цепи снова выбираем против часовой стрелки.
Рис. 3. Конденсатор в цепи переменного тока
Как и ранее, обозначим через заряд той пластины конденсатора, на которую течёт положительный ток — в данном случае это будет правая пластина. Тогда знак величины совпадает со знаком напряжения . Кроме того, как мы помним из предыдущего листка, при таком согласовании знака заряда и направления тока будет выполнено равенство .
Напряжение на конденсаторе равно напряжению источника:
Отсюда
Дифференцируя это равенство по времени, находим силу тока через конденсатор:
(3)
Графики тока и напряжения представлены на рис. 4. Мы видим, что сила тока каждый раз достигает максимума на четверть периода раньше, чем напряжение. Это означает, что фаза силы тока на больше фазы напряжения (ток опережает по фазе напряжение на ).
Рис. 4. Ток через конденсатор опережает по фазе напряжение на
Найти сдвиг фаз между током и напряжением можно также с помощью формулы приведения:
Используя её, получим из (3):
И теперь мы чётко видим, что фаза тока больше фазы напряжения на .
Для амплитуды силы тока имеем:
Таким образом, амплитуда силы тока связана с амплитудой напряжения соотношением, аналогичным закону Ома:
где
Величина называется ёмкостным сопротивлением
конденсатора. Чем больше ёмкостное сопротивление конденсатора, тем меньше амплитуда тока, протекающего через него, и наоборот.
Ёмкостное сопротивление обратно пропорционально циклической частоте колебаний напряжения (тока) и ёмкости конденсатора. Попробуем понять физическую причину такой зависимости.
1. Чем больше частота колебаний (при фиксированной ёмкости ), тем за меньшее время по цепи проходит заряд ; тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление. При ёмкостное сопротивление стремится к нулю: . Это означает, что для тока высокой частоты конденсатор фактически является коротким замыканием цепи.
Наоборот, при уменьшении частоты ёмкостное сопротивление увеличивается, и при имеем . Это неудивительно: случай отвечает постоянному току, а конденсатор для постоянного тока представляет собой бесконечное сопротивление (разрыв цепи).
2. Чем больше ёмкость конденсатора (при фиксированной частоте), тем больший заряд проходит по цепи за то же время (за ту же четверть периода); тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление.
Подчеркнём, что, в отличие от ситуации с резистором, мгновенные
значения тока и напряжения в одни и те же моменты времени уже не будут удовлетворять соотношению, аналогичному закону Ома. Причина заключается в сдвиге фаз: напряжение меняется по закону синуса, а сила тока — по закону косинуса; эти функции не пропорциональны друг другу. Законом Ома связаны лишь
амплитудные
значения тока и напряжения.
§ 50. Основные величины, характеризующие переменный ток
Переменная э. д. с., переменное напряжение, а также переменный ток характеризуются периодом, частотой, мгновенным, максимальным и действующим значениями. Период.
Время, в течение которого переменная э. д. с. (напряжение или ток) совершает одно полное изменение по величине и направлению (один цикл), называется
периодом
. Период обозначается буквой
Т
и измеряется в секундах. Если одно полное изменение переменной э. д. с. совершается за 1/50
сек
, то период этой э. д. с. равен 1/50
сек
.
Частота.
Число полных изменений переменной э. д. с. (напряжения или тока), совершаемых за одну секунду, называется
частотой
. Частота обозначается буквой
f
и измеряется в герцах (
гц
). При измерении больших частот пользуются единицами килогерц (
кгц
) и мегагерц (
Мгц
); 1
кгц
= 1000
гц
, 1
Мгц
= 1000
кгц
, 1
Мгц
= 1 000 000
гц
= 106
гц
. Чем больше частота переменного тока, тем короче период. Таким образом, частота — величина, обратная периоду.
Пример.
Длительность одного периода переменного тока равна 1/500
сек
. Определить частоту тока. Решение. Одно полное изменение переменного тока происходит за 1/500
сек
. Следовательно, за одну секунду совершится 500 таких изменений. На основании этого частота
Чем больше период переменного тока, тем меньше его частота. Таким образом, период является величиной, обратной частоте, т. е.
Пример.
Частота тока равна 2000
гц
(2
кгц
). Определить период этого переменного тока. Решение. За 1
сек
происходит 2000 полных изменений переменного тока. Следовательно, одно полное изменение тока — один период совершается за 1/2000 долю секунды. Но основании этого период
Угловая частота.
При вращении витка в магнитном поле один его оборот соответствует 360°, или 2π радиан. (1
рад
= 57° 17′ 44″; π = 3,14.) Если, например, виток за время
Т
= 3
сек
совершает один оборот, то угловая скорость его вращения за одну секунду
Соответственно угловая скорость вращения этого витка выражается в рад/сек
и определяется отношением Эта величина называется
угловой частотой
и обозначается буквой ω. Таким образом,
Так как частота переменного тока то, подставляя это значение f
в выражение угловой частоты, получим:
Угловая частота ω, выраженная в рад/сек
, больше частоты тока
f
, выраженной в герцах, в 2π раз. Если частота переменного тока
f
= 50
гц
, то угловая частота
ω = 2πf
= 2 · 3,14 · 50 = 314
рад/сек
В различных областях техники применяют переменные токи самых разных частот. На электростанциях СССР установлены генераторы, вырабатывающие переменную электродвижущую силу, частота которой f
= 50
гц
. В радиотехнике и электронике используют переменные токи частотой от десятков до многих миллионов герц.
Мгновенное и максимальное значения.
Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют
мгновенными значениями
этих величин и обозначают соответственно строчными буквами (
e, i, u, p
).
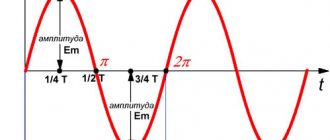
Максимальным значением
(амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается
Е
m, напряжения —
U
m, тока —
I
m. На рис. 51 видно, что переменная э. д. с. достигает своего значения два раза за один период.
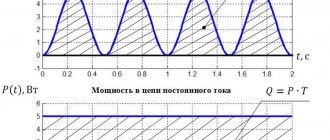
Действующая величина.
Электрический ток, протекающий по проводам, нагревает их независимо от своего направления. В связи с этим тепло выделяется не только в цепях постоянного тока, но и в электрических цепях, по которым протекает переменный ток. Если по проводнику сопротивлением
r ом
протекает переменный электрический ток, то в каждую секунду выделяется определенное количество тепла. Это количество тепла прямо пропорционально максимальному значению переменного тока. Можно подобрать такой постоянный ток, который, протекая по такому же сопротивлению, что и переменный ток, выделял бы равное количество тепла. В этом случае можно сказать, что в среднем действие (эффективность) переменного тока по количеству выделенного тепла равно действию постоянного тока. Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла. Электроизмерительные приборы (амперметр, вольтметр), включенные в цепь переменного тока, измеряют соответственно действующее значение тока и напряжения. Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.
Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.
По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:
E
m =
E
· 1,41;
U
m =
U
· 1,41;
I
m =
I
· 1,41; (55)
Пример.
Вольтметр, подключенный к зажимам цепи, показывает действующее напряжение
U
= 127
в
. Вычислить максимальное значение (амплитуду) этого переменного напряжения. Решение. Максимальное значение напряжения больше действующего в раз, поэтому
U
m =
U
· = 127 · 1,41 = 179,07
в
Для характеристики каждой переменной электродвижущей силы, переменного напряжения или переменного тока недостаточно знать период, частоту и максимальное значение.
Фаза. Сдвиг фаз.
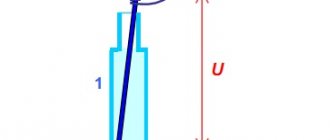
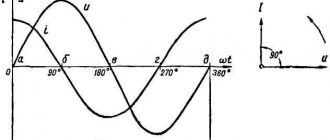
При сопоставлении двух и более переменных синусоидальных величин (э. д. с., напряжения или тока) необходимо также учитывать, что они могут изменяться во времени неодинаково и достигать своего максимального значения в разные моменты времени. Если в электрической цепи ток изменяется во времени так же, как меняется э. д. с., т. е. когда электродвижущая сила равна нулю и ток в цепи равен нулю, а при увеличении э. д. с. до положительного максимального значения одновременно увеличивается и достигает положительной максимальной величины и сила тока в цепи, и далее, когда э. д. с. уменьшается до нуля и сила тока одновременно станет равна нулю и т. д., то в такой цепи переменная электродвижущая сила и переменный ток совпадают по фазе. На рис. 52 показаны моменты вращения двух проводников в магнитном поле и графики изменения э. д. с. в проводах. Провод
1
и провод
2
смещены на угол φ = 90°. При пересечении магнитного потока в каждом из проводов возникает переменная э. д. с. Когда в проводе
2
электродвижущая сила равна нулю, в проводе
1
она будет максимальной. В проводе
2
э. д. с. постепенно увеличивается и достигает максимального значения в момент
t
1, а в проводе
1
индуктируемая э. д. с. постепенно убывает и в этот же момент времени равна нулю. Таким образом, индуктируемые в проводах э. д. с. не совпадают по фазе, а сдвинуты одна относительно другой по фазе на 1/4 периода или на угол φ = 90°. Кроме того, э. д. с. в проводе
1
раньше достигает максимума, чем э. д. с. в проводе
2
, и поэтому считают, что электродвижущая сила
е
1 опережает по фазе э. д. с.
е
2 или э. д. с.
е
2 отстает по фазе от э. д. с.
е
1. При расчетах цепей переменного тока важное практическое значение имеет сдвиг фаз между переменными напряжением и током.
предыдущая страница
| оглавление | следующая страница |
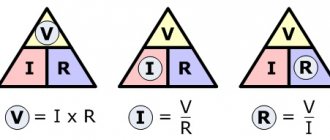
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.