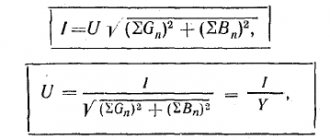Переменный ток
(AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.
Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток. Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока. Такой вариант можно представить как переменный ток AC
с постоянной составляющей
DC
. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.
DC
— Direct Current — постоянный ток, не меняющий своей величины и направления.
В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC
) для периодически меняющегося электрического тока любой формы. Тогда величина
DC
будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей
AC
.
При синусоидальной форме тока, например в электросети, постоянная составляющая DC
равна нулю.
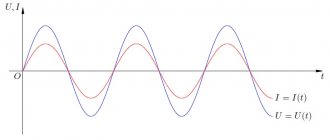
Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка. Запись AC+DC
в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности. Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей
DC
и среднеквадратичного значения переменной составляющей
AC
.
Термины AC
и
DC
применимы как для тока, так и для напряжения.
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период
T
— время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота
f
— величина, обратная периоду, равная количеству периодов за одну секунду. Один период в секунду это один герц (1 Hz). Частота
f =
1
/T
Циклическая частота
ω
— угловая частота, равная количеству периодов за
2π
секунд.
ω = 2πf = 2π/T
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза
ψ
— величина угла от нуля (
ωt
= 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение
— величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени
t
.
i = i(t); u = u(t)
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени. Например, синусоидальный ток или напряжение можно выразить функцией:
i = Iampsin(ωt); u = Uampsin(ωt)
С учётом начальной фазы:
i = Iampsin(ωt + ψ); u = Uampsin(ωt + ψ)
Здесь Iamp
и
Uamp
— амплитудные значения тока и напряжения.
Амплитудное значение
— максимальное по модулю мгновенное значение за период.
Iamp = max|i(t)|; Uamp = max|u(t)|
Может быть положительным и отрицательным в зависимости от положения относительно нуля. Часто вместо амплитудного значения применяется термин амплитуда
тока (напряжения) — максимальное отклонение от нулевого значения.
Среднее значение
(avg) — определяется как среднеарифметическое всех мгновенных значений за период
T
.
Среднее значение является постоянной составляющей DC
напряжения и тока. Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение
— среднеарифметическое модулей всех мгновенных значений за период.
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.
Для синусоидального тока и напряжения амплитудой Iamp
(
Uamp
) среднеквадратичное значение определится из расчёта:
Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока. В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.
Частные случаи значений амплитуды силы тока
В том случае, если цепь состоит только из активного сопротивления $(R)$, тогда:
ток совпадает с напряжением по фазе, амплитуда силы тока в этом случае равна:
Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы
Если сравнивать уравнение (6) с выражением (3), то можно сделать вывод о том, что если вместо конденсатора участок цепи просто закоротить, то это будет означать переход к емкости равной бесконечности.
Пусть в контуре можно сопротивлением пренебречь $(R=0)$, а емкость считать равной бесконечности, тогда:
Величину $X_L$ называют реактивным индуктивным сопротивлением (индуктивным сопротивлением), если она равна:
Из формулы следует, что индуктивность постоянному току не сопротивляется (при $\omega$=0, $X_L$=0).
Допустим, что $R=0,\ L=0.$ Тогда согласно формуле (3), получим:
Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор.
В том случае, если R=0, амплитуда силы тока равна:
Реактивным сопротивлением (реактансом) $(X)$ называют величину равную:
Параметры синусоидальных электрических величин
Синусоидальные ЭДС, напряжения и токи можно изображать графически в виде соответствующих синусоид, такие графики в электротехнике называют волновыми диаграммами (см. рис. 13).
Обычно на одной волновой диаграмме изображают несколько синусоид переменных величин (напряжений, токов), относящихся к одной и той же цепи. Для оценки их взаимного расположения вдоль оси абсцисс вводится разность их начальных фаз, называемая фазовым сдвигом. Чаще всего встречается фазовый сдвиг между током и напряжением.
Волновые диаграммы не всегда удобны для исследования, особенно при сложных разветвленных цепях. Проще в этом случае изображать синусоидальные величины вращающимися векторами. Изобразим вращающийся вектор, соответствующий току:
Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (точка на рисунке).
Комплексное число (соответствующее точке ) имеет вещественную (ОС) и мнимую (ОВ) составляющие на комплексной плоскости.
Переменный (синусоидальный) ток и основные характеризующие его величины.
Переменный ток (англ. alternating current — AC) — электрический ток
, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
Период Т— это время, за которое совершается одно полное колебание.
f = 1/T
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Источник
Среднее значение напряжения
Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
среднее значение напряжения за период
Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.
То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.
меандр
Средневыпрямленное значение напряжения
Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.
средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.
На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:
выпрямленное переменное напряжение после диодного моста
Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:
Параметры синусоидальных электрических величин
Широкое применение в электрических цепях электро-, радио- и других установок находят периодические ЭДС, напряжения и токи. Периодические величины изменяются во времени ( i=i(t); u=u(t)
) по значению и направлению, причем эти изменения повторяются через некоторые равные промежутки времени Т, называемые периодом (рис.13).
Наибольшее распространение получили токи, изменяющиеся по синусоидальному (гармоническому) закону.
Синусоидальный ток характеризуется следующими параметрами:
В европейских странах в качестве стандартной промышленной частоты принята f = 50 Гц, в США и Японии f = 60 Гц.
Разность начальных фаз двух синусоидальных величин одинаковой частоты ( ) называется сдвигом фаз между ними:
Синусоидальный ток имеет ряд преимуществ перед постоянным током, в связи с чем он получил очень широкое распространение:
а) его легко трансформировать из одного напряжения в другие,
б) при передаче на большие расстояния (сотни и тысячи километров) от источника до потребителя при многократной трансформации напряжение остается неизмененным, т.е. синусоидальным,
в) с его помощью может быть достаточно просто получено вращающееся магнитное поле, используемое в синхронных и асинхронных машинах.
Для количественной оценки синусоидальных функций времени вводятся понятия действующего и среднего значений. Действующим значением синусоидального тока называется величина такого постоянного тока, который оказывает эквивалентное тепловое действие. Действующие значения обозначаются I,U,E,P
Аналогично для напряжения и ЭДС
Подавляющее большинство приборов, измеряющих синусоидальные токи и напряжения проградуированы в действующих значениях.
Средним значением синусоидального тока или напряжения и ЭДС называется средняя за полупериод времени:
Амплитудные значения синусоидальных величин обозначаются: Im,Um,Em,Pm
Источник
Среднеквадратичное значение напряжения
Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.
Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды Ka:
Вот некоторые значения коэффициента амплитуды Ka для некоторых сигналов переменного напряжения:
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.