| Angular frequency | |
| ω | |
| Dimension | T −1 |
| Units | |
| SI | rad/s |
| GHS | rad/s |
| Other units | degree/s |
Angular frequency
(synonyms: radial frequency, cyclic frequency, circular frequency, rotational frequency) is a scalar physical quantity, a measure of the frequency of rotational or oscillatory motion. In the case of rotational motion, the angular frequency is equal to the magnitude of the angular velocity vector. In the International System of Units (SI) and the GHS system, angular frequency is expressed in radians per second, its dimension is the inverse of the dimension of time (radians are dimensionless).
The angular frequency is the time derivative of the oscillation phase:
ω = ∂ φ / ∂ t .
Another common notation is ω = φ ˙. >.>
The angular frequency is related to the frequency ν by the relation [1]
ω = 2 π ν . u >.>
If we use degrees per second as the unit of angular frequency, the relationship to ordinary frequency is as follows:
ω = 360 ∘ ν . u >.>
In the case of rotational motion, the angular frequency is numerically equal to the angle through which the rotating body will rotate per unit time (that is, equal to the magnitude of the angular velocity vector), in the case of oscillatory motion, the increment in the total phase of the oscillation per unit time. Numerically, the angular (cyclic) frequency is equal to the number of cycles (oscillations, revolutions) in 2 π units of time.
The introduction of cyclic frequency (in its main dimension - radians per second) allows us to simplify many formulas in theoretical physics and electronics. Thus, the resonant cyclic frequency of the oscillatory LC
-circuit is equal to ω LC = 1 / LC, =1/>,> while the usual resonant frequency is ν LC = 1 / (2 π LC). u _=1/(2pi >).>
At the same time, a number of other formulas become more complicated. The decisive consideration in favor of cyclic frequency was that the conversion factors 2 π and 1/(2 π), which appear in many formulas when using radians to measure angles and phases, disappear when cyclic frequency is introduced.
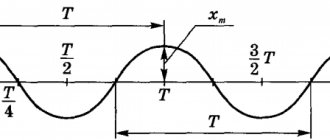
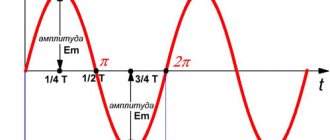
The amplitude of oscillations (Latin amplitude - magnitude) is the greatest deviation of an oscillating body from its equilibrium position.
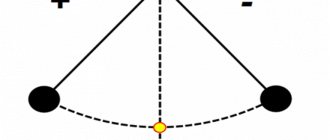
For a pendulum, this is the maximum distance that the ball moves away from its equilibrium position (figure below). For oscillations with small amplitudes, such a distance can be taken as the length of the arc 01 or 02, and the lengths of these segments.
The amplitude of oscillations is measured in units of length - meters, centimeters, etc. On the oscillation graph, the amplitude is defined as the maximum (modulo) ordinate of the sinusoidal curve (see figure below).
Oscillation frequency.
Oscillation frequency is the number of oscillations performed per unit of time, for example, 1 s.
The SI unit of frequency is named hertz (Hz) in honor of the German physicist G. Hertz (1857-1894). If the oscillation frequency (v) is 1 Hz, this means that one oscillation occurs every second. The frequency and period of oscillations are related by the relations:
.
cyclic or circular frequency is also used . It is related to the usual frequency v and the oscillation period T by the relations:
.
Cyclic frequency is the number of oscillations completed in 2π seconds.
Special cases of formulas for calculating cyclic frequency
A load on a spring (a spring pendulum is an ideal model) performs harmonic oscillations with a circular frequency equal to:
$k$ is the spring elasticity coefficient; $m$ is the mass of the load on the spring.
Small oscillations of a physical pendulum will be approximately harmonic oscillations with a cyclic frequency equal to:
where $J$ is the moment of inertia of the pendulum relative to the axis of rotation; $a$ is the distance between the center of mass of the pendulum and the suspension point; $m$ is the mass of the pendulum.
An example of a physical pendulum is a mathematical pendulum. The circular frequency of its oscillations is equal to:
The angular frequency of damped oscillations is found as:
where $\delta $ is the attenuation coefficient; in the case of damped oscillations, $_0$ is called the natural angular frequency of oscillations.
Movement examples
Oscillatory motion is one of the most common in nature. For example, you can imagine the strings of a musical instrument, a swing, or a person's vocal cords.
In physics, oscillations are processes that repeat at regular intervals. Such movements are considered through several models:
- a body suspended on a spring (moving up and down);
- weight on a string;
- electrical circuit and others.
Sound
Sound is vibrations of an elastic medium perceived by the organ of hearing.
Conditions necessary for the occurrence and sensation of sound:
- presence of a sound source;
- the presence of an elastic medium between the sound source and receiver;
- presence of a sound receiver; • the vibration frequency must be in the audio range;
- The sound power must be sufficient for perception.
Sound waves are elastic waves that cause a person to feel the sensation of sound, representing zones of compression and rarefaction that are transmitted over a distance over time.
Classification of sound waves:
- infrasound (\( \nu \) < 16 Hz);
- audio range (16 Hz < \( \nu \) < 20,000 Hz);
- ultrasound (\( \nu \) > 20,000 Hz).
The speed of sound is the speed of propagation of the oscillation phase, i.e., the region of compression and rarefaction of the medium.
The speed of sound depends
- on the elastic properties of the medium:
in air – 331 m/s, in water – 1400 m/s, in metal – 5000 m/s;
- depending on the ambient temperature:
in air at a temperature of 0°C - 331 m/s, in air at a temperature of +15°C - 340 m/s.
Characteristics of sound wave
- Loudness is a quantity characterizing a person’s auditory sensations, depending on the amplitude of vibrations in the sound wave. Units of measurement are dB (decibel).
- Pitch is a value that characterizes a person’s auditory sensations, depending on the frequency of vibrations in the sound wave. The higher the frequency, the higher the sound. The lower the frequency, the lower the sound.
- Timbre is the color of sound.
Musical sound is the sound produced by a harmoniously vibrating body. Each musical tone corresponds to a specific length and frequency of the sound wave. Noise is a chaotic mixture of tones.
Amplitude, period and frequency
If you simultaneously hang two weights on two different threads and launch them, you will notice that the distance of deviation of the load from the middle position to the extreme position is different.
This quantity is called amplitude. It is designated by the letter A and is measured in the C system in meters. also used to denote such a movement :
- The time it takes for the pendulum to reach the same position is called the period of oscillation.
- The number of oscillations per unit time is frequency. It is measured in Hertz (Hz). It has an inverse relationship with the period.
- The cyclic frequency of oscillations (angular, circular) is the number of oscillations in 2 π seconds. Denoted by the Greek letter omega. It is introduced to simplify calculations in theoretical physics and electronics. The unit of cyclic frequency is rad/s.
- If there are two graphs of functions with the same frequency, but shifted relative to each other, then their oscillation phase is different.
Links and notes[edit]
- ^ab Cummings, Karen; Halliday, David (2007). Understanding Physics. New Delhi: John Wiley & Sons Inc. Authorized reprint for Wiley - India. pp. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1)
- Holzner, Stephen (2006). Physics for Dummies. Hoboken, NJ: Wiley Publishing Inc., p.201. ISBN 978-0-7645-5433-9. angular frequency.
- Lerner, Lawrence S. (1996-01-01). Physics for Scientists and Engineers. p. 145. ISBN 978-0-86720-479-7.
- Mohr, J.C.; Phillips, W. D. (2015). "Dimensionless units in SI". Metrology
.
52
(1): 40–47. arXiv: 1409.2794. Bibcode: 2015Metro..52…40M. DOI: 10.1088/0026-1394/52/1/40. S2CID 3328342. - Jump up
↑ Mills, I. M. (2016).
"In units of radians and cycle for plane angle quantities." Metrology
.
53
(3):991–997. Bibcode: 2016Metro..53..991M. DOI: 10.1088/0026-1394/53/3/991. - "SI units need to be reformed to avoid confusion". From the editor. Nature
.
548
(7666):135. August 7, 2011. doi:10.1038/548135b. PMID 28796224. - PR Bunker; I.M. Mills; Per Jensen (2019). "Planck's constant and its units." J Quant Spectrosc Radiat Transfer
.
237
: 106594. doi: 10.1016/j.jqsrt.2019.106594. - PR Bunker; Per Jensen (2020). "Plank's Constant Action A." J Quant Spectrosc Radiat Transfer
.
243
: 106835. doi: 10.1016/j.jqsrt.2020.106835. h {\displaystyle h} - Serway, Raymond A.; Jewett, John W. (2006). Fundamentals of Physics (4th ed.). Belmont, CA: Brooks/Cole - Thomson Learning. pp. 375, 376, 385, 397. ISBN 978-0-534-46479-0.
- Nahvi, Mahmoud; Edminister, Joseph (2003). Essay on the theory and problems of electrical circuits by Schaum. McGraw-Hill Professional. pp. 214, 216. ISBN 0-07-139307-2.(LC1)
Related reading:
- Olenick, Richard P.; Apostle, Tom M.; Goodstein, David L. (2007). Mechanical Universe. New York: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8.
Math pendulum
This model considers the movement of a load suspended on a thread. A system is described in which the mass of the thread is much less than the mass of the load, and its length is much greater than its dimensions.
Also, the thread should be weightless and inextensible.
The load in this case is considered a material point.
If these conditions are met, the pendulum's oscillation frequency and period will not depend on the mass of the load. The movement of a mathematical pendulum is considered at a small angle of deflection (α). The latter is measured in radians, and therefore approximately corresponds in value to its sine and tangent. The same angle is proportional to the ratio of the displacement to the length of the thread:
α=x/l.
The pendulum is acted upon by the sine component of gravity and the tangent force of tension in the thread. According to Newton's second law: ma=-mgsin (α). Where can I get a=-gx/l
The second derivative of the equation of motion gives a=-(ω)^2x
Thus: -gx/l=-(ω)^2x -> ω ^2=g/l.
Period: T=2π /ω T=2π*sqrt (g/l)
This is Galileo's formula, which describes the movement of a mathematical pendulum.
Formula for oscillation frequency for a mathematical pendulum: v=sqrt (l/g)/2π .
Resonance
Resonance is the phenomenon of a sharp increase in the amplitude of oscillations, which occurs when the frequency of the driving force and the natural frequency of oscillations of the body coincide.
Resonance condition:
\( v_0 \) – natural frequency of oscillations of the pendulum.
The figure shows resonance curves for media with different friction. The less friction, the higher and sharper the resonance curve.
The phenomenon of resonance is taken into account under periodically changing loads in machines and various structures. Resonance is also used in acoustics, radio engineering, etc.
Spring pendulum
A similar term refers to a system in which movement is performed by a load suspended on a light spring.
The body is in equilibrium if the spring is not deformed. If it is stretched or compressed, the system will begin to oscillate under the action of an elastic force, which is aimed at bringing the pendulum to an equilibrium position.
The elastic force is proportional to the displacement of the body (x), but is directed in the opposite direction. The proportionality coefficient between these two quantities is called the spring stiffness (k). Thus:
F=-kx.
The elastic force reaches its greatest value in the position of maximum deviation of the body (amplitude, displacement) from equilibrium. At this point the acceleration is greatest.
As the body approaches the equilibrium position, the elastic force and acceleration decrease. At the midpoint, both quantities are equal to zero , but the speed of the body has a non-zero value. Therefore, the load does not stop, but continues to move.
After passing the equilibrium position, it moves in the opposite direction by inertia, and the elastic force pulls it back. Due to air friction, the speed decreases and the pendulum stops.
All these models can be classified as a classical harmonic oscillator - a system that has one degree of freedom and is described by a single equation.
Examples[edit]
Circular motion[edit]
Main article: Circular motion
In a rotating or orbital object, there is a relationship between distance from the axis, tangential velocity, and angular frequency. In one period, the body, making a circular motion, covers a distance. This distance is also equal to the circumference of the path traversed by the body, . Equating these two quantities and recalling the relationship between period and angular frequency, we obtain: } ω = v / r . {\displaystyle \omega =v/r.}
Spring vibrations[edit]
| Part of the series on |
| Classical mechanics |
| F = dd t ( m v ) {\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})} Second Law of Motion |
|
branches
|
Basics
|
Compositions
|
Main themes
|
Rotation
|
Scientists
|
| Categories ► Classical mechanics |
|
An object attached to a spring may vibrate. If we assume that the spring is ideal and massless without damping, then the movement will be simple and harmonious with the angular frequency given by [9]
ω = km , {\displaystyle \omega ={\sqrt {\frac {k}{m}}},}
where
k
is the spring stiffness,
m
is the mass of the object.
ω is called the natural frequency (which can sometimes be written as ω 0 ).
When an object vibrates, its acceleration can be calculated using the formula
a = − ω 2 x , {\displaystyle a=-\omega ^{2}x,}
where x
— displacement from the equilibrium position.
Using a "normal" rpm frequency, this equation would be
a = − 4 π 2 f 2 x . {\displaystyle a=-4\pi ^{2}f^{2}x.}
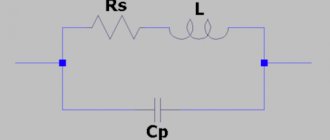
LC circuits[edit]
The resonant angular frequency in a series LC circuit is equal to the square root of the reciprocal of the product of the capacitance ( C,
measured in farads) and loop inductance (
L
, in SI units - Henry): [10]
ω = 1 LC.
{\displaystyle \omega ={\sqrt {\frac {1}{LC}}}.} Adding series resistance (for example, due to wire resistance in a coil) does not change the resonant frequency of the series LC circuit. For a parallel tuned circuit, the above equation is often a useful approximation, but the resonant frequency does depend on the losses in the parallel elements.
Oscillatory circuit
Is another example of the oscillation on which all radios are based. The circuit plays the role of a signal receiver.
In the simplest example, it is a closed circuit of an inductor and a capacitor. Under certain circumstances, electrical oscillations can occur and be maintained in such a circuit.
To excite oscillations, it is necessary to connect a constant voltage source to the capacitor and charge it. After this, remove the source and close the circuit.
The capacitor is discharged through the inductor, and a current is created in the circuit, the intensity of which increases as the capacitor is discharged. A magnetic field is created around the coil.
The electrical charge of the capacitor was converted into a magnetic field. After this, the magnetic field of the coil will decrease, and the capacitor will be charged back. The process is repeated cyclically and is described by the same characteristics as mechanical vibrations: frequency, amplitude and period.
They are free and damping. To maintain them, it is necessary to periodically charge the capacitor .
Wavelength
Wavelength is the distance over which a wave propagates in one period, i.e. it is the shortest distance between two points in the medium oscillating in the same phases. Designation – \( \lambda \), units of measurement – m.
The distance between adjacent crests or troughs in a transverse wave and between adjacent thickenings or rarefaction in a longitudinal wave is equal to the wavelength.
The speed of wave propagation is the speed of movement of humps and troughs in a transverse wave and thickenings or discharges in a longitudinal wave.