What is the instantaneous amplitude and effective value of alternating current?

How to find the amplitude value of AC voltage?

In our household electrical network, the current, effective, alternating current voltage Ud is equal to 220 volts. The maximum amplitude value of the voltage in the network is: Um = Ua = Ud x 1.41 = 220 x 1.41 = 310.2 volts.

Interesting materials:

How to properly turn off PSP? How to take disciplinary action correctly? How is advance payment and salary paid correctly? How to grow ginger correctly? How to properly grow a ficus from a shoot? How to properly grow a chestnut from a nut? How to properly take a shoot from a ficus? How to properly fix polycarbonate to a greenhouse? How to close a company correctly? How to close roses correctly?

Answer

Expert tested

We are talking about alternating current.

Instantaneous value (EMF or voltage or current) is the value of a quantity at a given moment in time. denoted most often in small letters: e, u, i.

The amplitude value (EMF or voltage or current) is the maximum value. Indicated by:

The effective value differs from the maximum in that it is less than the maximum by a factor, i.e. (using the example of current, for voltage and EMF it is similar):

The current value is indicated either without an index or with an index “d”:

(Russian “d” only).

The meaning of the effective value: with alternating current (i), the same amount of heat is released over a period as is released at the effective value

The current value is shown by devices connected to an alternating current circuit.

Average value of quantities (-//-) is the arithmetic average value of a quantity for half a period.

The maximum value (amplitude) of current and voltage is the greatest value that they reach in one period. The maximum value of current and voltage is indicated: voltage - Um, current - Im.

The magnitude of the variable current and voltage for any arbitrary moment in time is called the instantaneous value of this quantity. Instantaneous values of variable quantities are denoted by lowercase letters of the Latin alphabet, for example, electric current and electric voltage i and u, respectively.

The effective value of the alternating current is equal to the value of the equivalent direct current, which, passing through the same resistance as the alternating current, releases the same amount of heat over a period.

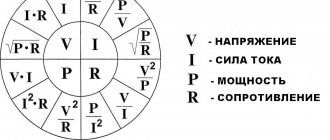
Ohm's Law for Typical Connections

Resistors, inductive coils, capacitors are connected in several ways:

all three elements are sequential;
all three - in parallel;
two - in parallel, the third - in series with them.

The notation of Ohm's law does not change, the only difference is in the formula for total resistance.

For circuits with active, reactive elements, it is called complete or complex, and is denoted by the symbol Z.

Since a phase shift occurs on the capacitor or coil, we consider not the resistances themselves, but their squares.

The coil has active resistance as a conductor, and inductive resistance as a manifestation of electromagnetic induction.

A circuit of resistor and coils is designated RL. In the case of a series connection, the impedance is:

Z = √(R2 + RL2) = √(R2 + (ωL)2);

Dependency I for this case:

I = U/Z = U/√(R2 + ω2L2);

The section with the resistor and capacitor is an RC circuit. For serial connection:

Z = √(R2 + RC2) = √(R2 + (1/ωC)2);

Dependency of quantities for this connection:

I = U/Z = U/√(R2 + (1/ωC)2)

To connect all elements in series (RLC circuit), the impedance value is:

Z = √(R2 + (RL – RC)2) = √(R2 + (ω2L2 – (1/ω2C2)2)).

The complex resistance of a parallel connection is found from the expression:

1/Z2 = 1/R2 + 1/(RL2 – RC2).

Knowledge of the characteristics of the flow of an alternating signal in a circuit with a capacitor or inductive coil helps in the calculation of radio circuits. Reactive elements are used in high and low pass filters. The phenomenon of vibrations and resonance is widely used in modern communications.

Vector image of sinusoidally varying quantities

On the Cartesian plane, from the origin of coordinates, draw vectors equal in magnitude to the amplitude values of sinusoidal quantities, and rotate these vectors counterclockwise ( in TOE this direction is taken to be positive

) with angular frequency equal to
w
.
The phase angle during rotation is measured from the positive semi-axis of abscissa. The projections of the rotating vectors onto the ordinate axis are equal to the instantaneous values of the emf e 1
and
e 2
(Fig. 3).
A set of vectors depicting sinusoidally varying emfs, voltages and currents is called vector diagrams.
When constructing vector diagrams, it is convenient to locate the vectors for the initial moment of time
( t = 0),
which follows from the equality of the angular frequencies of sinusoidal quantities and is equivalent to the fact that the Cartesian coordinate system itself rotates counterclockwise at a speed
w
. Thus, in this coordinate system the vectors are stationary (Fig. 4). Vector diagrams have found wide application in the analysis of sinusoidal current circuits. Their use makes circuit calculations more clear and simple. This simplification lies in the fact that addition and subtraction of instantaneous values of quantities can be replaced by addition and subtraction of the corresponding vectors.

Sinusoidally varying current

Of all the possible forms of periodic currents, the sinusoidal current is most widespread. Compared to other types of current, sinusoidal current has the advantage that it allows, in general, the most economical production, transmission, distribution and use of electrical energy. Only when using sinusoidal current is it possible to keep the shapes of voltage and current curves unchanged in all sections of a complex linear circuit. The theory of sinusoidal current is the key to understanding the theory of other circuits.

Ohm's law for an inductor

An inductive magnetic field inhibits the movement of free charges along a conductor. This is the reason for the additional (induction) resistance. It depends on the inductance L, the signal frequency:

RL = ωL,

where RL is inductive reactance.

The dependence of the characteristics for the section of the circuit with the inductor takes the form:

I = U/RL.

The inductor has a special feature: in it, the voltage fluctuations and the rate of charge change differ in phase.

Voltage fluctuations lead current fluctuations by a quarter of a period:

u = Umsinωt, i = Imsin(ωt – π/2).

The difference between the values of the sin function for 2 oscillations is called the phase shift. For inductive coil:

ωt – (ωt – π/2) = π/2 = 90°.

For clarity, the phase shift Δφ is depicted in the form of a vector diagram. The section of the circuit in which a phase difference occurs between current and voltage fluctuations is called a reactive load.

Self-induced emf

When an alternating electric current passes through the coil, an alternating magnetic field is generated, which is characterized by a changing magnetic flux that induces an emf. This phenomenon is called self-induction.

Due to the fact that the magnetic flux is proportional to the intensity of the electric current, then the formula for the self-induction emf looks like this:

Ф = L x I, where L is inductance, which is measured in H. Its value is determined by the number of turns per unit length and the size of their cross section.

Ohm's law for a circuit section with a capacitor

For a constant signal, the capacitor presents an insurmountable obstacle. The alternating signal passes through it with some effort. It is called capacitance.

It depends on the electrical capacity of the capacitor, the signal frequency and is inversely proportional to the product:

RC = 1/ωC.

Designations:

RC – capacitance;
ω – angular frequency;
C is the capacitance of the capacitor.

The dependence of the values for the section of the circuit with a capacitor is written as follows:

I = U/RC.

Capacitor is a reactive load. Voltage fluctuations and charge change rates are not synchronous. The change in U lags behind the fluctuations in I by a quarter of a period:

u = Umsinωt, i = Imsin(ωt + π/2).

The phase shift is 90°. Inductive and capacitive loads shift phase in opposite directions.

Alternating current has not found practical use for a long time. This was due to the fact that the first electrical energy generators produced direct current, which fully satisfied the technological processes of electrochemistry, and direct current motors have good control characteristics. However, as production developed, direct current became less and less suitable for the increasing requirements for economical power supply. Alternating current made it possible to effectively split electrical energy and change the voltage using transformers. It became possible to produce electricity at large power plants with its subsequent economical distribution to consumers, and the radius of power supply increased.

Currently, the central production and distribution of electrical energy is carried out mainly on alternating current. Circuits with changing - alternating - currents have a number of features compared to direct current circuits. Alternating currents and voltages cause alternating electric and magnetic fields. As a result of changes in these fields in circuits, the phenomena of self-induction and mutual induction arise, which have the most significant impact on the processes occurring in the circuits, complicating their analysis.

Alternating current (voltage, emf, etc.) is a current (voltage, emf, etc.) that changes over time. Currents whose values are repeated at regular intervals in the same sequence are called periodic.

and the shortest period of time through which these repetitions are observed is
the period T.
For a periodic current we have

(1)

The reciprocal of the period is the frequency,

measured in Hertz (Hz):

(2)

The range of frequencies used in technology: from ultra-low frequencies (0.01-10 Hz - in automatic control systems, in analog computer technology) - to ultra-high frequencies (3000 ¸ 300000 MHz - millimeter waves: radar, radio astronomy). In the Russian Federation, industrial frequency f
= 50Hz
.

The instantaneous value of a variable is a function of time. It is usually denoted by a lowercase letter:

— instantaneous current value;

– instantaneous voltage value;

— instantaneous value of EMF;

— instantaneous power value.

The largest instantaneous value of a variable over a period is called amplitude (it is usually denoted by a capital letter with the index m

— current amplitude;

— voltage amplitude;

— EMF amplitude.

RMS value of alternating current

The value of a periodic current equal to the value of direct current, which during one period will produce the same thermal or electrodynamic effect as the periodic current, is called the effective value

periodic current:

(3)

The effective values of EMF and voltage are determined similarly.

Sinusoidally varying current

Representation of sinusoidal EMF, voltages
and currents on the Cartesian coordinate plane
Sinusoidal currents and voltages can be depicted graphically, written using equations with trigonometric functions, represented as vectors on the Cartesian plane or complex numbers.

Shown in Fig. 1, 2 graphs of two sinusoidal EMF e1

and
e2
correspond to the equations:

The values of the arguments of sinusoidal functions and are called
the phases
of sinusoids, and the value of the phase at the initial moment of time
( t = 0):
and -
the initial phase
().

The quantity characterizing the rate of change of the phase angle is called the angular frequency.

Since the phase angle of a sinusoid

changes by rad
T f is
the frequency.

When considering two sinusoidal quantities of the same frequency together, the difference in their phase angles, equal to the difference in the initial phases, is called the phase shift angle

For sinusoidal EMF e1

and
e2
phase angle:

Vector image of sinusoidally
varying quantities
On a Cartesian plane, from the origin of coordinates, draw vectors equal in magnitude to the amplitude values of sinusoidal quantities, and rotate these vectors counterclockwise ( in TOE this direction is taken as positive

) with angular frequency equal to
w
.
The phase angle during rotation is measured from the positive semi-axis of abscissa. The projections of the rotating vectors onto the ordinate axis are equal to the instantaneous values of the emf e1
and
e2
(Fig. 3).
A set of vectors depicting sinusoidally varying emfs, voltages and currents is called vector diagrams.
When constructing vector diagrams, it is convenient to locate the vectors for the initial moment of time
( t = 0),
which follows from the equality of the angular frequencies of sinusoidal quantities and is equivalent to the fact that the Cartesian coordinate system itself rotates counterclockwise at a speed
w
. Thus, in this coordinate system the vectors are stationary (Fig. 4). Vector diagrams have found wide application in the analysis of sinusoidal current circuits. Their use makes circuit calculations more clear and simple. This simplification lies in the fact that addition and subtraction of instantaneous values of quantities can be replaced by addition and subtraction of the corresponding vectors.

Let, for example, at the branch point of the circuit (Fig. 5) the total current is equal to the sum of the currents and two branches:

Each of these currents is sinusoidal and can be represented by the equation

And .

The resulting current will also be sinusoidal:

Determining the amplitude and initial phase of this current by means of appropriate trigonometric transformations turns out to be quite cumbersome and not very visual, especially if a large number of sinusoidal quantities are summed. This is much easier to do using a vector diagram.

In Fig.
Figure 6 shows the initial positions of the current vectors, the projections of which onto the ordinate axis give the instantaneous current values for t=0.
When these vectors rotate with the same angular velocity
w,
their relative position does not change, and the phase shift angle between them remains equal.

Since the algebraic sum of the projections of vectors onto the ordinate axis is equal to the instantaneous value of the total current, the vector of the total current is equal to the geometric sum of the current vectors:

Plotting a vector diagram to scale allows you to determine the values of and from the diagram, after which a solution for the instantaneous value can be written by formally taking into account the angular frequency: .

Representation of sinusoidal EMF, voltages and currents by complex numbers

Geometric operations with vectors can be replaced by algebraic operations with complex numbers, which significantly increases the accuracy of the results obtained.

Each vector on the complex plane corresponds to a certain complex number, which can be written in:

indicative

trigonometric

algebraic

-
forms.
For example, EMF shown in Fig. 7 by a rotating vector, corresponds to a complex number

The phase angle is determined by the projections of the vector on the axes “+1” and “+j” of the coordinate system, as

In accordance with the trigonometric form of notation, the imaginary component of a complex number determines the instantaneous value of a sinusoidally varying EMF:

(4)

It is convenient to represent a complex number as the product of two complex numbers:

(5)

Parameter corresponding to the vector position for t =0

(or on a complex plane rotating at speed
w
), is called
the complex amplitude:
, and the parameter is
the complex of the instantaneous value.
The parameter is the rotation operator

vector by an angle
w t
relative to the initial position of the vector.

Generally speaking, multiplying a vector by the rotation operator is its rotation relative to its original position by an angle ± a

Therefore, the instantaneous value of the sinusoidal quantity is equal to the imaginary part without the sign “ j”

product of the amplitude complex and the rotation operator:

The transition from one form of writing a sinusoidal quantity to another is carried out using the Euler formula:

(6)

If, for example, the complex voltage amplitude is given as a complex number in algebraic form:

- then to write it in exponential form, it is necessary to find the initial phase, i.e. the angle formed by the vector with the positive semi-axis +1:

Then the instantaneous voltage value:

Where .

When writing the expression, for definiteness it was assumed that , i.e. that the image vector is in the first or fourth quadrants. If , then at (second quadrant)

(7)

and at (third quadrant)

(8)

(9)

If the instantaneous value of the current is given in the form , then the complex amplitude is written first in exponential form, and then (if necessary) using Euler’s formula, they proceed to the algebraic form:

It should be noted that when adding and subtracting complexes, you should use the algebraic form of writing them, and when multiplying and dividing, the exponential form is convenient.

So, the use of complex numbers allows us to move from geometric operations on vectors to algebraic operations on complexes. So, when determining the complex amplitude of the resulting current from Fig. 5 we get:

Where ;

Effective value of sinusoidal EMF, voltages and currents

In accordance with expression (3), for the effective value of the sinusoidal current we write:

A similar result can be obtained for sinusoidal emfs and voltages. Thus, the effective values of sinusoidal current, EMF and voltage are less than their amplitude values by a factor of:

(10)

Since, as will be shown below, energy calculations of alternating current circuits are usually carried out using effective values of quantities, by analogy with the previous one we introduce the concept of an effective value complex

Literature

1. Basics

circuit theory: Textbook. for universities /G.V. Zeweke, P.A. Ionkin, A.V. Netushil, S.V. Strakh. –5th ed., revised. –M.: Energoatomizdat, 1989. -528 p.

2. Bessonov L.A.

Theoretical foundations of electrical engineering: Electric circuits. Textbook for students of electrical engineering, energy and instrument engineering specialties of universities. –7th ed., revised. and additional –M.: Higher. school, 1978. –528 p.

Test questions and tasks

1. What is the practical meaning of depicting sinusoidal quantities using vectors?

2. What is the practical meaning of representing sinusoidal quantities using complex numbers?

3. What are the advantages of representing sinusoidal quantities using complexes compared to their vector representation?

4. For given sinusoidal functions of emf and current, write down the corresponding complexes of amplitudes and effective values, as well as complexes of instantaneous values.

5. In Fig. 5, a. Define .

Answer: .

Image of sinusoidal emfs, voltages and currents on the Cartesian coordinate plane

Sinusoidal currents and voltages can be represented graphically, written using equations with trigonometric functions, represented as vectors on a Cartesian plane or complex numbers.

Shown in Fig. 1, 2 graphs of two sinusoidal EMF e 1

and
e 2
correspond to the equations:
.

The values of the arguments of sinusoidal functions are called the phases
of sinusoids, and the value of the phase at the initial moment of time
( t = 0):
and -
the initial phase
().

Size

, which characterizes the rate of change of the phase angle, is called
the angular frequency.
Since the phase angle of a sinusoid

changes by rad
T f is
the frequency.

When considering two sinusoidal quantities of the same frequency together, the difference in their phase angles, equal to the difference in the initial phases, is called the phase shift angle

.
.

Definition of electromagnetic induction

The occurrence of an electric current in a conductor moving in a magnetic field is called the phenomenon of induction in moving conductors. When a conductor moves in a magnetic field, its free electrons move relative to the conductor under the influence of the Lorentz force. The phenomenon of electromagnetic induction was discovered by Faraday in 1831 in a conducting circuit. He noticed that in a closed conducting circuit, when the flux of magnetic induction changes through the surface that the circuit limits, an electric current appears. This is also the phenomenon of electromagnetic induction, the resulting current in the circuit is called induction .
So, the phenomenon of electromagnetic induction consists in the occurrence of an electric current in a closed conductor when the flux of magnetic induction covered by the circuit changes. In this case, the circuit can be stationary.

Are you an expert in this subject area? We invite you to become the author of the Directory Working Conditions