| Карта сайта |
Известная также, как векторный анализ. А кому-то векторный анализ, известный как теория поля =) Наконец-то мы добрались до этой интереснейшей темы! Данный раздел высшей математики язык не поворачивается назвать простым, однако ж, в грядущих статьях я постараюсь достигнуть двух целей:
а) чтобы все понимали, о чём вообще идёт разговор;
б) и чтобы «чайники» научились решать, как минимум, простые вещи – хотя бы на уровне заданий, которые предлагаются студентам-заочникам.
Весь материал будет изложен в популярном стиле, и если вам нужна более строгая и полная информация, то можно взять, например, 3-й том Фихтенгольца или заглянуть в Вики.
И сразу расшифруем заголовок. С теорией, думаю, всё понятно – в лучших традициях сайта мы разберём её основы и сделаем основной упор на практику. Ну а с чем у вас ассоциируется слово «поле»?
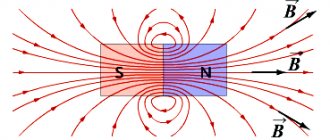
Поле с травой, футбольное поле…. Ещё? Поле деятельности, поле экспериментов. Приветствую гуманитариев! …Из школьного курса? Электрическое поле, магнитное, электромагнитное…, так, хорошо. Гравитационное поле Земли, в котором мы находимся. Отлично! Так, кто это там сказал о поле действительных и комплексных чисел? …совсем какие-то монстры здесь собрались! =) Благо, алгебра уже пройдена.
На ближайших уроках мы познакомимся со специфическим понятием поля, конкретными примерами из жизни, а также научимся решать тематические задачи векторного анализа. Теорию поля лучше всего изучать, как вы правильно догадываетесь, на поле – природе, где есть лес, речка, озеро, деревенский домик, и я приглашаю всех погрузиться если и не в тёплую летнюю реальность, то в приятные воспоминания:
ПолЯ в рассматриваемом сегодня смысле бывают скалярные и векторные, и начнём мы с их «кирпичиков».
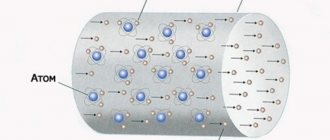
Во-первых, скаляр. Довольно-таки часто этот термин ошибочно отождествляют с числом. Нет, всё обстоит немного не так: скаляр – это величина, каждое значение которой может быть выражено лишь одним числом. В физике примеров масса: длина, ширина, площадь, объём, плотность, температура и др. Всё это скалярные величины. И, кстати, масса – тоже пример.
Во-вторых, вектор. Алгебраического определения вектора я коснулся на уроке о линейных преобразованиях и одну из его частных ипостасей не знать просто невозможно =) Типичный вектор выражается двумя или бОльшим количеством чисел (своими координатами). И даже для одномерного вектора лишь одного числа не достаточно – по той причине, что у вектора есть ещё направление. И точка приложения, если вектор не свободен. Векторами характеризуют силовые физические поля, скорость и многие другие величины.
Ну что же, теперь можно приступить к сбору алюминиевых огурцов урожая:
Скалярное поле
Если каждой точке некоторой области пространства поставлено в соответствие определённое число (чаще действительное), то говорят, что в этой области задано скалярное поле.
Рассмотрим, например, исходящий из земли перпендикулярный луч. Воткните для наглядности лопату =) Какие скалярные поля можно задать на этом луче? Первое, что напрашивается – это поле высоты – когда каждой точке луча поставлена в соответствие её высота над уровнем земли. Или, например, поле атмосферного давления – здесь каждой точке луча соответствует числовое значение атмосферного давления в данной точке.
Теперь подойдём к озеру и мысленно проведём над его поверхностью плоскость. Если каждой точке «водного» фрагмента плоскости поставить в соответствие глубину озера, то, пожалуйста – скалярное поле задано. В этих же точках можно рассмотреть и другие скалярные величины, например, температуру поверхности воды.
Важнейшим свойством скалярного поля является его инвариантность относительно системы координат. Если перевести на человеческий язык, то с какой бы стороны мы на лопату / озеро ни посмотрели – скалярное поле (высота, глубина, температура и т.д.) от этого не изменятся. Более того, скалярное поле, скажем, глубины можно ведь задать и на другой поверхности, например, на подходящей полусфере, или непосредственно на самой водной поверхности. А почему нет? Разве нельзя каждой точке полусферы, расположенной над озером, поставить в соответствие число? Плоскость я предложил исключительно ради удобства.
Добавим ещё одну координату. Возьмите в руку камень. Каждой точке этого камня можно поставить в соответствие его физическую плотность. И опять – в какой бы системе координат мы его ни рассмотрели, как бы ни крутили в руке – скалярное поле плотности останется неизменным. Впрочем, некоторые люди могут оспорить этот факт =) Такой вот философский камень.
С чисто математической точки зрения (вне физического или другого частного смысла) скалярные поля традиционно задают нашими «обычным» функциями одной , двух , трёх и бОльшего количества переменных. При этом в теории поля в широком ходу традиционные атрибуты этих функций, такие как, область определения, линии и поверхности уровня.
Так, линии уровня глубины озера представляют собой замкнутые непересекающиеся линии на плоскости. Каждая из этих линий соответствует определённому значению глубины, и по соответствующей «плоской» карте мы можем судить о рельефе дна – где мелководье, где «обрывы» и т.д.
Поверхности уровня представляют собой непересекающиеся пространственные поверхности, «вложенные» друг в друга. Или «лежащие» друг на друге. Или… у кого на что фантазии хватит =) Каждой такой поверхности соответствует постоянное значение скалярного поля, например, какая-то конкретная температура.
Однако наши «обычные» числа и функции задают скалярные поля далеко не всегда! Приведу классический пример с вектором – для определённости рассмотрим геометрический вектор плоскости в некоторой аффинной системе координат. Что произойдёт, если перейти к новому базису? В общем случае данный вектор поменяет координаты: .
Координаты вектора – это числа? Числа. Но скалярными величинами они не являются! Поскольку скаляры не зависят от системы координат. Более того, координаты векторов можно ведь задать и «обычными» функциями – и эти функции не будут порождать скалярное поле!
Надо сказать, ловким получился переход к следующему параграфу:
Векторное поле
Если каждой точке некоторой области пространства поставлен в соответствие вектор с началом в данной точке, то говорят, что в этой области задано векторное поле.
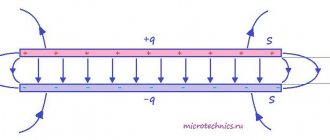
Из чего следует, что элементы векторного поля не свободны, то есть «привязаны» к точкам. И почему векторы в «неволе» – становится ясно из простых примеров. В частности, на уроке о криволинейных интегралах по замкнутому контуру мы провели «плоский» опыт с магнитом на столе: чем ближе к магниту поднести железку, тем сильнее она притягивается. И эта сила в той или иной точке поверхности стола как раз характеризуется вектором напряжённости магнитного поля. Чем сильнее притяжение, тем длиннее вектор, ну и его остриё, понятно, указывает направление действия силы.
Но гораздо чаще векторные поля рассматривают в трёхмерном пространстве, пожалуйста: наша Земля – тот же больший магнит. Другой пример – её гравитационное поле. Чем дальше от поверхности, тем меньше сила тяжести и тем короче соответствующие силовые векторы. Кстати, куда они «смотрят»? Говоря просто, все они направлены к центру нашей планеты.
Большую группу векторных полей образуют так называемые поля скоростей. Посмотрите на поле (которое с травкой) и мысленно очертите над ним произвольную пространственную область. Представьте, что над полем дует ветер – небольшой такой ураганчик для пущей наглядности. Теперь зафиксируем некоторый момент времени и каждой точке построенной области поставим в соответствие несвободный вектор, который характеризует:
а) направление движения воздуха в данной точке; б) и скорость его движения в данной точке – чем выше скорость, тем длиннее вектор. Если в какой-то точке штиль, то ей сопоставляется нулевой вектор.
Множество этих векторов и образует векторное поле скорости ветра в данный момент времени.
Аналогично устроено поле скоростей течения жидкости – так, например, каждой точке реки в некоторый момент времени можно поставить в соответствие вектор, указывающий направление и скорость течения жидкости в этой точке.
Да чего там ветер и река, поле скорости можно смоделировать собственноручно, для этого достаточно взмахнуть рукой. Или даже моргнуть глазом.
…Какой же кошмар! – векторы вокруг нас! В «ужастиках» эту роль играют зомби или живые мертвецы, а в реальности-то вот оно, оказывается как – ВЕКТОРЫ.
С формально-математической точки зрения, векторные поля задают векторными функциями, которые уже «проскакивали» в других темах:
Для «плоского» случая – это векторная функция , которая различным точкам плоскости * ставит в соответствие несвободные векторы – конкретный пример есть в параграфе Работа векторного поля. Если функции двух переменных определены при любых «икс», «игрек», то векторное поле будет задано на всей плоскости .
* Далее по умолчанию считаем, что все дела происходят в декартовой системе координат
С трёхмерным пространством всё аналогично: – здесь каждой допустимой точке пространства ставится в соответствие вектор с началом в данной точке. «Допустимость» определяется областями определения функций , и если каждая из них определена при всех «икс», «игрек», «зет», то векторное поле будет задано во всём пространстве.
! Обозначения: векторные поля также обозначают буквой либо , а их компоненты через либо соответственно.
Из вышесказанного давно и очевидно следует, что, по меньшей мере математически, скалярные и векторные поля можно определить и во всём пространстве. Однако с соответствующими физическими примерами я всё же поостерёгся, поскольку таких понятий, как температура, гравитация (или других) ведь где-то может и вовсе не существовать. Но это уже не ужасы, а научная фантастика =) И не только фантастика. Ибо внутри камней ветер, как правило, не дует.
Следует отметить, что векторные поля (те же поля скоростей) с течением времени могут меняться, и поэтому во многих физических моделях рассматривают дополнительную независимую переменную . Кстати, то же самое касается и скалярных полей – температура же, в самом деле, тоже не «застыла» во времени.
Однако в рамках математики мы ограничимся троицей , и при «встрече» таких полей будем подразумевать некоторый фиксированный момент времени либо время, за которое поле не успело измениться.
Векторные линии
Если скалярные поля описываются линиями и поверхностями уровня, то «форму» векторного поля можно охарактеризовать векторными линиями. Наверное, многие помнят этот школьный опыт: под лист бумаги помещаются магнит, а наверх (смотрим!) высыпаются железные опилки, которые как раз и «выстраиваются» по линиям поля.
Постараюсь сформулировать попроще: каждая точка векторной линии является началом вектора поля, который лежит на касательной в данной точке:
Разумеется, векторы линии в общем случае имеют разную длину, так на приведённом рисунке, при перемещении слева направо их длина растёт – здесь можно предположить, что мы приближаемся, например, к магниту. В силовых физических полях векторные линии так и называют – силовыми линиями. Другой, более простой пример – это гравитационное поле Земли: его силовые линии представляют собой лучи с началом в центре планеты, причём векторы силы тяжести расположены прямо на самих лучах.
Векторные линии скоростных полей называются линями тока. Множество линий тока даёт нам представление о потоке жидкости или газа в данный момент времени. К слову, линия тока и траектория движения частицы – это не одно и то же. Если поле скоростей не меняется с течением времени (например, река с устоявшимся течением), то, да – мусоринки будут плыть по линиям тока. Такое поле называют стационарным, и в нём траектории движения частиц совпадают с линиями тока. Но представьте пыльную бурю – здесь линии тока в каждый момент разные, и поэтому мусоринка будет лететь по своей уникальной траектории, а вовсе не по какой-то конкретной линии тока.
Вообще, многие понятия теории поля пришли из гидродинамики, с чем мы ещё не раз столкнёмся.
Если «плоское» векторное поле задано ненулевой функцией , то его силовые линии можно найти из дифференциального уравнения . Решение данного уравнения задаёт семейство векторных линий на плоскости . Иногда в задачах требуется изобразить несколько таких линий, что обычно не вызывает затруднений – выбрали несколько удобных значений «цэ», начертили какие-нибудь там гиперболы, и порядок.
С пространственным векторным полем ситуация занятнее. Его силовые линии определяются соотношениями . Здесь нужно решить систему двух дифференциальных уравнений и получить два семейства пространственных поверхностей. Линии пересечения этих семейств и будут пространственными векторными линиями. Если все компоненты («пэ», «ку», «эр») отличны от нуля, то существует несколько технических способов решения. Я не буду рассматривать все эти способы (т.к. статья разрастется до неприличных размеров), а остановлюсь на распространённом частном случае, когда одна из компонент векторного поля равна нулю. Давайте сразу распишем все варианты:
если , то нужно решить систему ; если , то систему ; и если , то .
И что-то непозволительно давно у нас не было практики:
Пример 1
Найти силовые линии векторного поля
Решение: в данной задаче , поэтому решаем систему:
Первый диффур вообще халява: – семейство плоскостей, параллельных координатной плоскости (представили в уме!).
Второй диффур – почти она же:), ну а зачем нам скоропостижные трудности? – семейство (внимание!) параболических цилиндров, параллельных оси .
Ответ: искомое множество векторных линий:
Иными словами, здесь в каждой плоскости «сидит» семейство парабол .
Аналогичная задачка для самостоятельного решения:
Пример 2
Найти силовые линии векторного поля
Охарактеризуйте получившееся множество линий. Кстати, в условии явно не сказано, о каком поле идёт речь – плоском или пространственном. В подобных ситуациях рекомендую решать задачу для пространства – не ошибётесь 
Краткое решение и ответ в конце урока.
Векторное поле градиентов
В каких отношениях вы находитесь с производной по направлению и градиентом? …ничего страшного, от ненависти до любви – один шаг =) Напоминаю, что градиент функции в точке – это несвободный вектор, указывающий направление максимального роста функции в данной точке и определяющий скорость этого роста.
Нахождение векторной функции градиентов – есть популярный и распространённый способ получить из скалярного поля поле векторное. При условии существования соответствующих частных производных функции двух и трёх переменных:
Смысл очень прост. Так, если функция задаёт скалярное поле глубины озера, то соответствующая векторная функция определяет множество несвободных векторов, каждый из которых указывает направление наискорейшего подъёма дна в той или иной точке и скорость этого подъёма.
Если функция задаёт скалярное поле температуры некоторой области пространства, то соответствующее векторное поле характеризует направление и скорость наибыстрейшего прогревания пространства в каждой точке этой области.
Разберём общую математическую задачу:
Пример 3
Дано скалярное поле и точка . Требуется:
1) составить градиентную функцию скалярного поля;
2) найти градиент поля в точке и вычислить его длину;
3) вычислить производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.
Непосредственно к решению задачи это не относится, но сразу обратим внимание, что скалярное поле не определено на всех трёх координатных плоскостях .
1) Быстренько вспоминаем, как находить частные производные функции трёх переменных:
Составим функцию, которая определяет векторное поле градиентов:
И ещё раз – в чём её смысл? Полученная векторная функция каждой точке области определения скалярного поля ставит в соответствие вектор , указывающий направление и максимальную скорость роста функции в данной точке.
И один из таких векторов нам предстоит найти в следующем пункте:
2) Вычислим частные производные в точке :
Таким образом: – ещё раз подчёркиваю, что этот вектор исходит из точки , и перемещать его никуда нельзя! По той причине, что он характеризует направление наискорейшего возрастания функции именно в точке «эм нулевое», а не где-то ещё!
Мерилом же этой максимальной скорости как раз является длина градиента:
3) Вычислим производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.
Немного мудрёно, но разобраться немудренО. Во-первых, убедимся, что точка «эм нулевое» действительно принадлежит данной поверхности: Получено верное равенство. ОК.
Что это за поверхность – нас не интересует, нам важен её нормальный вектор в точке , да не абы какой, а образующий с полуосью тупой угол.
Вспоминаем материал ещё одного урока: вектор нормали к поверхности в точке задаётся следующим образом:
В данном случае:
Но нужный ли это вектор? Как выяснить угол, который он образует с полуосью ? …Сегодня у нас какой-то экскурс в фильмы… =) и сейчас на очереди фильм «Вспомнить всё». Вычислим скалярное произведение вектора с направляющим вектором положительной «зетовой» полуоси:
, следовательно, угол между этими векторами острый, что нас не устраивает!
И поэтому нужно выбрать противоположно направленный нормальный вектор:
Заметим заодно, что нормальные векторы в отличие от градиентов – свободны, их задача лишь указать направление.
Вычислим направляющие косинусы данного направления, или, что то же самое – координаты единичного вектора, сонаправленного с вектором :
Контроль:
Таким образом, искомая производная по направлению:
Напоминаю, что это значение характеризует скорость роста функции в точке по направлению вектора , и оно не может оказаться больше, чем (максимальной скорости роста в данной точке).
Ответ:
Небольшой пример для самостоятельного решения:
Пример 4
Найти угол между градиентами скалярных полей и в точке
Просто и со вкусом. …Как найти угол? – с помощью того же скалярного произведения. Ну и, очевидно, тут придётся «тряхнуть» многоэтажными дробями и некоторой тригонометрией. Краткое решение и ответ в конце урока.
Что делать, если вам предложено «плоское» скалярное поле ? Просто убавьте одну координату, соответствующие примеры можно найти в статье Производная по направлению и градиент функции. По существу, мы вновь прорешали примеры той статьи, только немного в другой интерпретации.
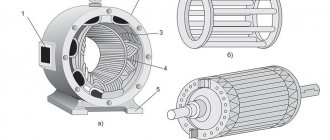
Статор в двигателе
Цилиндр статора интегрирован в корпус электромотора. Он является его неподвижной частью. Вместе статор и корпус составляют единый моноблок.
Сердечник статора набран из металлических пластин. Они изолированы одна от другой слоем лака. Назначение такого устройства сердечника – противодействие нагреву вихревыми токами Фуко.
В собранном виде пакет статора впрессовывают в корпус. Сердечник статора формируется витками обмотки.
Их пропивают субстанциями особого состава, защищающего витки от повреждений, и укладывают в специально выточенные во внутренней стенке цилиндра пазы.
Схема подключения статора к электрической сети выглядит следующим образом:
На корпусе двигателя имеется так называемый БРНО, блок расключения начал обмоток. Иначе говоря, это распределительная коробка, внутри которой находятся клеммники.
Конструктивно, они различаются между собой. Устройство клеммников зависит от мощности двигателя и вида работы, которую этот двигатель выполняет. Концевые части всех обмоток подключаются к клеммам БРНО.
От мощности электромотора и его функционального предназначения зависит также и способ подключения обмоток.
Есть два способа подключения. Один это так называемая«Звезда», другой — «Треугольник». От способа подключения зависит то, как будет работать электромотор.
При способе соединении «Звезда»мотор плавно увеличивает обороты, причем быстрый разгон оборотов до максимума невозможен.
А если обмотки соединены треугольником, мотор может сразу развить те обороты, на который он конструктивно рассчитан, но и стартовые токи будут адекватно велики.
Потенциальное векторное поле
На уроке Криволинейный интеграл по замкнутому контуру я уже подробно рассказал о «плоском» потенциальном поле, и поэтому перед дальнейшим чтением будет крайне полезно окинуть взглядом концовку указанной статьи. Фактически сейчас будет продолжение, где мы разбёрём аналогичную ситуацию в пространстве.
«Потенциальное»…, на ум здесь приходит потенциальная энергия, потенциальные возможности. Так, лежащий на подоконнике кирпич потенциально можно сбросить вниз, и вмятина на земле неиллюзорно продемонстрируют нам ту самую потенциальную энергию. Всё верно, гравитационное поле Земли – это один из ярких примеров потенциального векторного поля.
Вспомним его характерный признак, сбросив с подоконника нашего уютного деревенского домика…, нет, не кирпич, а пёрышко. Из точки до точки оно может пролететь по бесчисленному множеству траекторий (из-за ветра, по причине сопротивления воздуха и т.д.), но во всех случаях гравитационное поле Земли совершит одну и ту же работу по перемещению пера между этими точками. Ну а различные траектории – это уже «вклад» других сил, которые, к слову, тоже можно описать векторными полями.
Примечание: возможно, здесь у вас возник вопрос: «но ветер же может приподнимать перо, и тогда работа должна увеличиваться!». Ничего подобного. Физическое понятие работы не подразумевает, что кто-то или что-то «трудится». Если ветер приподнимает перо вверх, то он просто уменьшает абсолютную величину работы силы тяжести.
В физике есть конкретная математическая модель, описывающая гравитационные силы, но в соответствии с направленностью сайта, я приведу только общие формулы. Итак:
Векторное поле является потенциальным, если оно представляет собой поле градиентов некоторого скалярного поля . Функцию называют потенциальной функцией или просто потенциалом.
Работа потенциального векторного поля по перемещению материальной точки из точки в точку не зависит от траектории её движения и выражается следующим криволинейным интегралом 2-го рода:
, который равен разности потенциалов .
Иными словами, в потенциальном поле имеет значение лишь начальная и конечная точка маршрута. И если эти точки совпадают, то суммарная работа сил по замкнутому контуру будет равна нулю:
Давайте поднимем пёрышко с земли и доставим его в исходную точку. При этом траектория нашего движения опять же произвольная; можно даже бросить перо, снова его поднять и т.д.
Почему итоговый результат нулевой?
Перо упало из точки «а» в точку «бэ»? Упало. Сила тяжести совершила работу .
Перо попало обратно в точку «а»? Попало. А это значит, что была совершена точно такая же работа против сил тяжести, причём не важно с какими «приключениями» и какими силами – да хоть ветер задул его обратно.
Примечание: в физике знак «минус» символизирует противоположное направление.
Таким образом, суммарная работа сил равна нулю:
Как я уже отмечал, физическое и обывательское понятие работы отличаются. И это различие вам хорошо поможет понять не пёрышко и даже не кирпич, а, например, пианино 
Дружно поднимите пианино и спустите его по лестнице вниз. Потаскайте по улице. Сколько захочется и где захочется. И если никто не вызвал дурку занесите инструмент обратно. Вы поработали? Конечно. До седьмого пота. Но с точки зрения физики никакой работы не совершено.
Словосочетание «разность потенциалов» подмывает рассказать ещё о потенциальном электростатическом поле, но бить током своих читателей как-то уж совсем не гуманно =) Тем более, примеров – непочатый край, ибо потенциальным является любое градиентное поле, коих пруд пруди.
Но легко сказать «пруд пруди»: вот дано нам векторное поле – как определить, потенциально оно или нет?
Синхронные двигатели с постоянными магнитами на роторе: управление (синус и/или трапеция)
В продолжение темы модельно ориетированного проектирования, публикую очередную статью Калачева Юрия Николаевича, автора книги Моделирование в электроприводе. Инструкция по пониманию. Данный текст еще готовится к публикации в специализированных изданиях, но читатели хабра увидят его первые.
В зарубежной литературе можно встретить два термина, связанных с этими двигателями:
- PMSM (Permanent Magnet Synchronous Motor), что на языке Пушкина означает: синхронный двигатель c постоянными магнитами (СДПМ), и это понятно.
- BLDC (Brush Less Direct Current), что переводится с языка Шекспира, как Бесколлекторный (бесщеточный) Двигатель Постоянного Тока (БДПТ), и это непонятно. Причем здесь постоянный ток?
С этими названиями и у нас, и за рубежом существует немалая путаница.
Например, термин PMSM (СДПМ) может применяться для обозначения двигателя с постоянными магнитами на роторе, независимо от формы его ЭДС, но так же часто его применяют, подразумевая исключительно синусоидальную форму ЭДС двигателя.
Термин BLDC (БДПТ) может применяться для обозначения двигателя с постоянными магнитами на роторе и трапецеидальной ЭДС, а может вообще обозначать не двигатель, а некий мехатронный узел, включающий в себя:
- двигатель с постоянными магнитами и трапецеидальной ЭДС
- датчик положения ротора
- управляемый по сигналам этого датчика полупроводниковый коммутатор.
Собственно этот мехатронный узел, который может, как и двигатель постоянного тока, управляться постоянным напряжением и породил сам термин BLDC (БДПТ).
Ещё по отношению к синхронным двигателям с постоянными магнитами на роторе в отечественной литературе, можно встретить название «вентильный двигатель».
Попытки автора разобраться с этим термином быстро зашли в тупик, так как в различных источниках обнаружились явные противоречия.
Например, в книге Г.Б. Онищенко «Электрические двигатели» на стр. 47 «вентильным» называется двигатель соответствующий термину BLDC (БДПТ), что предполагает трапецеидальную ЭДС, и это понимаемо.
Но двигатели типа 5ДВМ сам производитель (ЧЭАЗ) называет «вентильными», хотя при этом утверждает, что они имеют синусоидальную ЭДС.
А вот википедия: «Вентильный двигатель следует отличать от бесколлекторного двигателя постоянного тока (БДПТ), который имеет трапецеидальное распределение магнитного поля в зазоре…».
Ну, … приехали …
Какой термин, какой форме ЭДС соответствует – непонятно.
А между тем, именно эта форма определяет выбор структуры системы управления двигателем.
Как человек занимающийся управлением этими двигателями хочу предложить:
- во избежание путаницы забыть термин «вентильный двигатель»
- термином БДПТ обозначать не двигатель, а исключительно описанный выше мехатронный узел (аналог двигателя постоянного тока)
- делить синхронные двигатели с постоянными магнитами на роторе (СДПМ) по типу ЭДС на две группы:
1) с синусоидальной ЭДС (далее, для краткости, — СДПМс)
2) с трапецеидальной ЭДС (далее, для краткости, — СДПМт)
Управление
При управлении двигателями с синусоидальной ЭДС используется векторное регулирование (подробно описано в книжке по ссылке). С точки зрения возможностей и качества управления это наилучший вариант.
Однако и двигатели с трапецеидальной ЭДС в силу более простой конструкции статорных обмоток и возможности более простого управления применяются довольно часто.
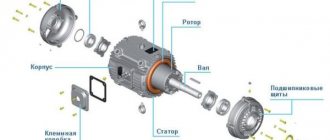
Конструкция двигателей
Форма ЭДС определяется конструкцией двигателя.
Ротор синхронных двигателей представляет собой магнит с различным количеством пар полюсов.
На Рис 1. показаны возможные конструкции статорных обмоток. Обычно синусоидальной ЭДС соответствует «распределенная» намотка, а трапецеидальной «сосредоточенная».
Рисунок 1. Конструкции статорных обмоток
Статорная обмотка двигателя с трапецеидальной ЭДС проще и технологичнее, за счёт этого цена такого двигателя несколько ниже.
Далее остановимся более подробно на двигателе с трапецеидальной ЭДС (СДПМт)
Двигатель с одной парой полюсов будет выглядеть в разрезе так, как показано на Рис.2.
Рисунок 2. Схема двигател с одной парой полюсов я в разрезе
На статоре СДПМт намотаны три обмотки (А, В, С), сдвинутые в пространстве на 120°. Каждая обмотка состоит из двух секций, включённых встречно. Таким образом, при протекании тока в обмотке она создаёт внутри двигателя два полюса (положительный и отрицательный), к которым и притягивается магнитный ротор. Поочередное изменение токов в обмотках переключает полюса обмоток и заставляет ротор двигаться вслед за полем. На этом и основан принцип работы двигателя.
В дальнейшем будем считать нулевым то угловое положение ротора при котором вектор потока ротора совпадает по направлению с осью фазы А (осью обмотки А).
Уравнения равновесия статорных обмоток СДПМт в системе АВС
Уравнения равновесия статорных обмоток двигателя при его включении в «звезду» в неподвижных фазных координатах АВС имеют вид (1).
Здесь:
- — фазные напряжения
- — потокосцепления фазных обмоток
- — токи фаз
- — активное сопротивление фазной обмотки.
Поток в обмотке каждой фазы формируется из следующих составляющих:
- поток, наводимый собственным током фазы
- поток, наводимый магнитными полями других фазных обмоток
- поток, наводимый в обмотке магнитами ротора.
Проиллюстрируем это системой (2):
- Где:
— индуктивность фазных обмоток
— взаимные индуктивности обмоток
— потокосцепления, наводимые в обмотках магнитом ротора.
В общем случае все индуктивности системы (2) могут являться переменными функциями угла поворота поля .
В частном случае для неявнополюсного двигателя (при цилиндрическом роторе) индуктивности и взаимные индуктивности обмоток не зависят от угла.
Обозначив — индуктивность фазной обмотки,
— взаимная индуктивность двух фазных обмоток, и подставив выражения (2) в систему (1), получим выражение (3):
Заметив, что производные по времени от потокосцеплений магнитов ротора
— есть не что иное, как наводимая магнитами
ротора в этих обмотках ЭДС, систему (3) можно переписать в виде (4).
Теперь введем понятие единичной функции формы ЭДС.
Единичная функция формы ЭДС — это функция от угла поля (), имеющая единичную амплитуду и повторяющая по форме ЭДС. Для фаз А,В,С обозначим эти функции: .
Используя единичные функции формы, мгновенные ЭДС в фазах можно представить выражением (5):
- Где:
— амплитуда потокосцепления ротора и фазной обмотки
— скорость вращения поля
— скорость вращения ротора
— число пар полюсов двигателя.
Зависимости единичных функций формы ЭДС обмоток СДПМт от угла поворота поля представлены На Рис.3.
Рис. 3. Единичные функции форм ЭДС
Вывод формулы для расчета электромагнитного момента СДПМт
Момент, создаваемый двигателем, является суммой моментов, создаваемых его обмотками.
Посмотрим на уравнение равновесия обмотки А из системы (4).
Умножив обе его части на ток обмотки, получим уравнение для мгновенной электрической мощности обмотки:
Рассмотрим составляющие этой мощности:
- — реактивная мощность обмотки
- — активная мощность, рассеивающаясяв обмотке
- — мощность, создающая электромагнитный момент.
Если пренебречь потерями при переходе электрической мощности в механическую, то можно записать:
- Где:
— электромагнитный момент двигателя
— угловая скорость вращения ротора.
Подставив в формулу (6) значения ЭДС из соотношений (5), получим формулу вычисления электромагнитного момента ротора (7).
Коммутация обмоток СДПМт
В соответствии с формулой (7) момент СДПМт пропорционален сумме произведений фазных токов на функции формы соответствующих ЭДС.
Максимальное значение ЭДС обмотки соответствует плоским участкам трапеции ЭДС. Если бы нам удалось на этих участках угловой траектории сформировать в обмотках токи некоторой постоянной амплитуды, например, совпадающие по знаку со знаком ЭДС, то это позволило бы сформировать при этих токах максимальный постоянный положительный момент.
Для примера рассмотрим на Рис.3 участок угловой траектории от π/6 до π/2. На этом участке ЭДС в фазе А имеет максимально отрицательное значение, а в фазе В максимально положительное. Следовательно, для получения положительного момента на этом участке угловой траектории надо обеспечить в фазе А отрицательное, а в фазе В положительное значение тока. Для этого фазу А можно подключить на отрицательный, а фазу В на положительный полюса внешнего источника постоянного напряжения (Udc). При этом фаза С не используется (отключена от источника Udc).
Величина тока, протекающего через обмотки, будет в свою очередь определяться прикладываемым к обмоткам напряжением, величиной ЭДС и параметрами обмоток.
Если рассуждать таким образом, то можно составить таблицу коммутаций обмоток, обеспечивающих в зависимости от положения ротора момент нужного знака (Табл. 1).
Таблица1. Закон коммутации
Обмотки трёхфазного двигателя можно коммутировать на внешний источник напряжения с помощью трехфазного мостового инвертора. Для этого состояние инвертора надо поставить в зависимость от положения ротора. Обычно это делается с помощью датчика положения ротора (ДПР). Этот датчик имеет три канала. Каждый канал выдает за один оборот двигателя импульс, соответствующий половине периода вращения, при этом импульсы в каналах сдвинуты на 120°.
Логическая обработка сигналов ДПР позволяет определить — в каком из шести секторов в данный момент находится ротор.
Работа ДПР поясняется Табл. 2.
Таблица 2. Работа ДПР (определение сектора)
Возможная структура системы управления моментом СДПМт
Алгоритм, описанный в Табл.1, предполагает протекание одного и того же тока в двух фазах двигателя при единичном значении функции формы ЭДС в обмотках фаз. Поэтому выражение (7) можно переписать в виде (8).
Где: — значение тока в фазах.
То есть значение момента пропорционально величине тока в обмотках двигателя.
Вытекающая из формулы (8) структура системы управления моментом в приводе с СДПМт изображена на Рис.4.
Рисунок 4. Система управления моментом БДПТ
Данная структура позволяет получить нужный момент, формируя в обмотках двигателя ток необходимой амплитуды, при сохранении алгоритма коммутации (Табл.1).
Эта задача решается с помощью создания на базе трёхфазного мостового инвертора контура тока с ШИМ.
Регулятор тока (ПИ-рег.) формирует сигнал задания напряжения обмоток (U), которое затем реализуется инвертором с ШИМ в соответствии с алгоритмом коммутации (Табл.1).
В качестве сигнала обратной связи в контуре можно использовать трёхфазно-выпрямленные сигналы датчиков тока фаз или сигнал датчика тока в звене постоянного тока инвертора ().
На основе рассмотренного канала управления моментом можно строить внешние контуры управления скоростью и положением.
Однако
Если бы токи в обмотках спадали до нуля и нарастали до нужного уровня мгновенно, то момент двигателя, определяемый их величиной, в установившемся режиме был бы постоянным. В действительности же реальные переходные процессы при коммутации обмоток приводят к пульсациям момента. В зависимости от параметров обмоток, а также соотношения величин текущей ЭДС и напряжения звена постоянного тока эти пульсации могут быть различны по длительности, амплитуде и знаку.
Кроме этих коммутационных пульсаций в рассматриваемой системе также будут иметь место пульсации момента на частоте ШИМ.
Ниже приведен пример работы модели системы регулирования скорости. Данная модель построена в среде SimInTech на элементах специализированного тулбокса «Электропривод». Среда позволяет получить максимальное приближение моделируемых процессов к реальности с учетом эффектов временной и уровневой дискретизации.
Часть модели, а именно — модель цифровой системы управления скоростью приведена ниже, на Рис.5. Регулятор скорости системы (Рег.W) выдает сигнал момента, который отрабатывается структурой, построенной в соответствии с Рис.4.
Рисунок 5. Модель цифровой системы управления
Для управления был выбран двигатель со следующими параметрами:
- Rs = 2.875 Ом — сопротивление обмотки фазы;
Ls = 8.5e-3 Гн – индуктивность фазы;
F = 0.175 Вб – потокосцепление ротора;
Zp = 4 — число пар полюсов;
Jr = 0.06 кг·м2 — момент инерции ротора.
Напряжение в звене постоянного тока привода было принято равным 100В.
В контуре тока электропривода использовалась ШИМ с частотой 5кГц.
В процессе регулирования происходило ступенчатое увеличение частоты при постоянном моменте сопротивления на валу двигателя (10 Нм).
Графики, полученные в процессе работы модели, приведены на Рис.6.
Рисунок 6. Моделирование работы двигателя
На графике момента видны существенные пульсации.
Отметим, что в основном они связаны именно с переходными процессами при коммутации обмоток и имеют соответственно частоту, ушестеренную по отношению к заданной.
Пульсации, связанные с ШИМ, в данном случае, невелики.
Заметим, что коммутационные пульсации существенно возрастают при увеличении момента, что связано с увеличением тока.
Несколько спасает то, что их влияние на скорость снижает инерция.
А можно ли векторно управлять СДПМт?
Если очень хочется — то можно. Однако и здесь не без особенностей. Математика и структура стандартной векторной системы управления исходит из синусоидальности поля в зазоре. При трапецеидальной ЭДС это условие нарушается, правда не очень сильно (трапеция это же почти синус).
А результатом этого «почти» будут, опять же, пульсации момента.
Вид модели цифровой системы векторного управления скоростью в среде SimInTech показан на Рис.7.
Рисунок 7. Часть модели векторного управления.
Ниже на Рис.8 показан график работы модели уже рассмотренного ранее СДПМт работающего в рассмотренном ранее режиме, но под управлением векторной системы.
В графике момента мы опять наблюдаем пульсации (хотя по сравнению с предыдущим вариантом они несколько уменьшились).
Причины пульсации при векторном управлении и управлении по ДПР различны, но частота все та же – ушестеренная по отношению к заданной.
Заметим, что вследствие несинусоидальности ЭДС токи в обмотках двигателя так же будут принципиально несинусоидальными (это так, хотя в масштабе рисунка и не слишком заметно).
Рисунок 8. Работа двигателя при векторном управлении
А можно ли с помощью коммутации обмоток по ДПР управлять двигателем с синусоидальной ЭДС?
С точки зрения автора можно – но не нужно.
Наряду с коммутационными пульсациями момента синусоидальность ЭДС (отсутствие плоской вершины трапеции) в данном случае неминуемо вызовет еще и дополнительные пульсации, снижающие качество регулирования даже по сравнению с управляемым по ДПР двигателем СДПМт.
А при векторном управлении двигателем с синусоидальной ЭДС пульсаций момента не будет.
Для подтверждения этого тезиса ниже (Рис.9) приведены графики работы модели двигателя с уже рассмотренными ранее параметрами, но с синусоидальной ЭДС и векторной системой управления скоростью.
Видно, что пульсации момента в этом случае практически отсутствуют. При правильной настройке регуляторов системы они связаны только с ШИМ-преобразованием и для данного случая почти не видны.
Рисунок 8. Работа двигателя с синусоидальной ЭДС
Итоги
Для синхронников с трапецеидальной ЭДС — коммутация по ДПР.
Так же возможно использование и более сложного векторного алгоритма регулирования, что может дать снижение уровня пульсации момента.
Для синхронников с синусоидальной ЭДС лучший вариант это векторное регулирование.
Это сочетание идеально для построения точного электропривода (что собственно и так было понятно).
Калачёв Ю.Н.
Модели для самостоятельного изучения можно взять здесь.
Предыдущие статьи по теме:
Модельно ориентированное проектирование. Электропривод с бесколлекторным двигателем постоянного тока
Модельно ориентированное проектирование. Построение активного выпрямителя (на основе математической модели)
Список литературы
[1] А. С. Пушкин «Полтава».