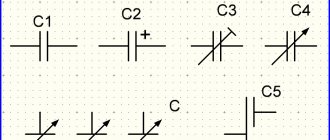Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.
Но прежде введём понятие электрической ёмкости.
Характеристики конденсатора
Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.
Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента.
Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.
Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.
Внешний вид устройств
Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.
Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.
Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает.
Условные обозначения
Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.
Идея суперконденсатора
Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Энергия конденсатора
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
| Энергия электростатического поля Wp = qEd Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] E — напряженность электрического поля [В/м] d — расстояние от заряда [м] |
В случае с конденсатором d будет представлять собой расстояние между пластинами.
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Поэтому:
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
| Энергия конденсатора Wp = qU/2 Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] U — напряжение на конденсаторе [В] |
| Энергия конденсатора Wp = q2/2C Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] C — электроемкость конденсатора [Ф] |
| Энергия конденсатора Wp = CU2/2 Wp — энергия электростатического поля [Дж] C — электроемкость конденсатора [Ф] U — напряжение на конденсаторе [В] |
Эти формулы справедливы для любого конденсатора.
Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца
Закон Кулона
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела.
В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.
Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
$F=k{|q_1|·|q_2|}/{r^2}$
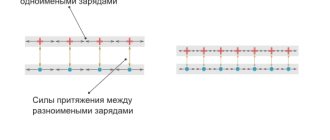
где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда.
Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.
То есть $1$ Кл$= 1А·с$.
Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
$k=9·10^9H·м^2$/$Кл^2$
Часто его записывают в виде $k={1}/{4πε_0}$, где $ε_0=8.85×10^{-12}Кл^2$/$H·м^2$ — электрическая постоянная.
Электрическая емкость конденсатора
Электроемкость
Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:
$C={q}/{φ}$
Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.
Единицей емкости в СИ является фарада
($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.
Электрический конденсатор
Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.
Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора.
Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что
поле в конденсаторе практически все сосредоточено между его обкладками.
Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:
$C={q}/{U}={ε_{0}εS}/{d}$
где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_{0}$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.
Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.
Энергия поля конденсатора
Энергия заряженного конденсатора
выражается формулами
$E_n={qU}/{2}={q^2}/{2C}={CU^2}/{2}$
которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.
Энергия электрического поля.
Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:
$ω={εε_{0}E^2}/{2}$
где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц.
Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
$I={∆q}/{∆t}$
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.
Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_{0}nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t={∆l}/{υ}$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
$I={∆q}/{∆t}={q_{0}nS∆l·υ}/{∆l}=q_{0}nυS$
В СИ единица силы тока является основной и носит название ампер
(А) в честь французского ученого А. М. Ампера (1755-1836).
Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.
Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Ома для участка цепи
Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.
Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.
Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи
. Математически закон Ома записывается в виде следующей формулы:
$I={U}/{R}$
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой
(ВАХ) проводника.
Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.
Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:
- сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
- сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.
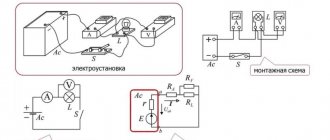
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления
называется
омом
(Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) —
это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
$R=ρ{l}/{S}$
где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.
Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.
Из формулы $R=ρ{l}/{S}$ следует, что
$ρ={RS}/{l}$
Величина, обратная $ρ$, называется удельной проводимостью
$σ$:
$σ={1}/{ρ}$
Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^{-1}м^{-1}$.
На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^{-6}$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^{-2}$) Ом$·$м$м^2$/м, диэлектрики — в $10^{15}-10^{20}$ раз большим.
Зависимость сопротивления от температуры
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.
Температурным коэффициентом
сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:
$α={R_t-R_0}/{R_0t}$
Зависимость удельного сопротивления проводников от температуры выражается формулой:
$ρ=ρ_0(1+αt)$
В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=({1}/{273})K^{-1}$. Для растворов электролитов $α
Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.
Параллельное и последовательное соединение проводников
Для параллельного соединения
проводников справедливы следующие соотношения:
1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом
), равен сумме токов в каждом из элементов цепи:
$I=I_1+I_2;$
2) напряжение $U$ на концах проводников, соединенных параллельно, одно и то же:
$U=U_1=U_2;$
3) при параллельном соединении проводников складываются их обратные сопротивления:
${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$
4) сила тока и сопротивление в проводниках связаны соотношением:
${I_1}/{I_2}={R_2}/{R_1}$
Для последовательного соединения проводников в цепи
справедливы следующие соотношения:
1) для общего тока $I$:
$I=I_1=I_2,$
где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т. е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;
2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:
$U=U_1+U_2;$
3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:
$R=R_1+R_2;$
4) также справедливо соотношение:
${U_1}/{U_2}={R_1}/{R_2}$
Работа электрического тока. Закон Джоуля-Ленца
Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:
$A=qU$
где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:
$A=IUt$
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Закон Джоуля-Ленца
Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:
$Q=I^2Rt$
Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.
Из закона Джоуля — Ленца следует, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это используется в технике, например, для распыления металлов.
При параллельном соединении все проводники находятся под одинаковым напряжением, но токи в них разные. Из формулы ($Q=I^2Rt$) следует, что, так как, согласно закону Ома $I={U}/{R}$, то
$Q={U^2t}/{R}$
Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.
Если в формуле ($A=IUt$) выразить $U$ через $IR$, воспользовавшись законом Ома, получим закон Джоуля-Ленца. Это лишний раз подверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.
Мощность электрического тока
Действие тока характеризуют не только работой $A$, но и мощностью $Р$. Мощность
тока показывает, какую работу совершает ток за единицу времени. Если за время $t$ была совершена работа $А$, то мощность тока $P={A}/{t}$. Подставляя в это равенство выражение ($A=IUt$), получаем:
$P=IU$
Это выражение можно переписать в разных формах, воспользовавшись законом Ома для участка цепи:
$P=IU=I^{2R}={U^2}/{R}$
Из соотношения для ЭДС легко получить мощность источника тока:
$P_ε=εI$
В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом
$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.
Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:
$Р=10А·220В=2200Вт=2.2кВт.$
Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.
В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком
(счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в
киловатт-часах
($кВт·ч$).
$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.
Энергия заряженного конденсатора
Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:
We=Q22C=CU22=QU2.
Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:
Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.
Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Плоский конденсатор.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
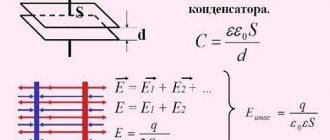
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
E = frac{sigma}{2varepsilon_0thinspacevarepsilon}
Здесь sigma— это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}
Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}
А какая же будет величина напряженности вне конденсатора? А все просто — слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Работа электрического поля
Электрическое поле называется потенциальным. Это значит, что работа его сил не зависит от траектории движения заряда, исключительно от энергии начального и конечного положения. Напомним, согласно определению:
Электрическое поле – это материя, посредством которой взаимодействуют электрические заряды.
Электрическое поле воздействует исключительно на электрические заряды. Создаётся двумя путями:
- Электрическими зарядами. Силовые линии начинаются на положительных и заканчиваются на отрицательных зарядах.
- Изменяющимся магнитным полем. При этом образуется электромагнитная волна, что используется в генераторах.
Когда говорят, что излучение приборов действует на человека, подразумеваются и магнитная, и электрическая составляющие. Особенно опасна первая, которая с большим трудом экранируется. Электрическое поле, рассматриваемое в физике школьного курса, считается стационарным, а линии напряжённости его параллельны. Приводятся два примера:
- Допустим, заряд перемещается вдоль линий поля на некоторое расстояние l. Тогда работа находится по упрощённой формуле A = Fl, где F – сила, действующая на заряд.
- Теперь предположим, что заряд переместился из прежней точки по косой линии. Так, что проекция пути lb на силовые линии снова равна l. Участок прямолинейный, угол отклонения – В. Работа вычисляется по формуле с учётом геометрических соотношений как A = FlbcosB = Fl.
Этот простой случай, легко распространяется на любую форму линий напряжённости. Сие означает, что в электрическом поле работа не зависит от траектории, а значит, равна разнице потенциалов поля: А = П1 – П2. Формула применима для любого поля. Чтобы адаптировать выражение, вводят понятие электрического потенциала как энергию единичного положительного заряда – ф = П / q1. Тогда формула для работы принимает иной вид.
Электрическим напряжением между двумя точками называется разница потенциалов между ними. Умножая указанное значение на величину заряда, поскольку величина удельная, получаем: А = (ф1 – ф2) q = U q. Потенциал через величины поля находится:
ф = q / 4 ε Пи r,
где q – величина заряда, создающего поля; ε – диэлектрическая проницаемость среды (для воздуха и вакуума равна единице); Пи = 3,14; r – расстояние до исследуемой точки от упомянутого заряда. Формула годится далеко не для любых случаев, приведена для примера. Допустимо применять для заряда, распределённого по поверхности шара, и точек, лежащих вне указанной поверхности.
Из истории
Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:
- Эвальд Георг фон Клейст (11 октября 1745 года).
- Питер ван Мушенбрук (1745 – 1746 годы).
Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.
Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.
Концепция Вольты
Как свидетельствуют записки учёного, уже в 1778 году он получил представление о разнице потенциалов, которые называл tension – напряжение. С 1775 года Вольта придерживается концепции электрической ёмкости – capacita, выдвинутой его учителем Беккарией. Вольта уже знает, что электрофорус способен накопить заряд, называет прибор конденсатором, и решает подтвердить теорию практикой. Иначе – найти взаимосвязь напряжения, ёмкости и объёмом (quantita) заряда.
Вольта начал с лейденской банки. Он заряжал её от статического генератора и пробовал определить энергию конденсатора тремя путями:
- Наблюдал получаемую искру электрической дуги от различной конструкции лейденских банок, заряженных одинаковым напряжением.
- Измерял количество произведённой электростатическими генераторами трения работу, пока показания электрометра не росли до определённого уровня.
- Разряжал лейденские банки на открытом воздухе и пытался сравнить производимый ими электрический шок по истечении времени.
Все перечисленное привело исследователя к странным выводам, что высокие лейденские банки более вместительные (при одинаковых площадях обкладок и прочих равных условиях). Вероятно, это связано со скоростью разряда их дуги на воздухе вследствие различий в кривизне поверхностей. Силу разряда Вольта увязывал с электрическим током: чем быстрее течёт флюид, тем более жаркий (по ощущениям) эффект. В результате, Вольта счёл, что разница потенциалов единственная определяет процесс возникновения удара. Он решил, что напряжение допустимо измерить двумя путями:
- Через количество оборотов генератора статического заряда.
- Сравнивая силу электрического удара при разряде лейденской банки.
Вольта нашёл, что заряжая пустую лейденскую банку от полной, шок получается вдвое слабее. Постепенно (1782 год) Вольта пришёл к выводу, что вышеуказанные величины соотносятся между собой: tension x capacity ~ load, в современном мире выглядит как U C = q или C = q / U.
Вольта заключил, что ёмкость больше там, где при меньшем напряжении вмещается больше заряда. Последовало заключение, что количество накопленного флюида прямо пропорционально площади обкладок плоского конденсатора. Что согласуется с современными формулами. Вольта обобщил знания на случай произвольного проводника (экспериментировал со стержнями лейденских банок). Изменяя расстояние между обкладками, установил:
С ~ S / d.
Что фактически стало выражением ёмкости плоского конденсатора. Вольта объяснил зависимость наличием некоего сопротивления (resistance) между обкладками, подразумевая воздух. Изменяя дистанцию, удаётся варьировать этот параметр в обе стороны. Это слегка не согласуется с современными концепциями, но Вольта помог Георгу Ому 40 лет спустя вывести зависимость между током и напряжением.
Фактически измерения проделывались на основе работы поля, проявлявшейся лишь вследствие заряда конденсатора. Очевидно, что указанная величина равна энергии – одной из первых физических характеристики, использованных для вывода аналитических выражений.
Мера энергии заряженного конденсатора
При расчёте фильтров цепей питания и прочих электрических фильтров встаёт задача определения номиналов. Кажется, достаточно взять формулу частоты резонансного контура, но простота обманчива. Легко убедиться, что одинаковому ответу соответствует множество значений. Которое выбрать?
Чем больше мощность источника, питания прибора, тем большая энергия здесь проходит в единицу времени. Для конденсатора она зависит от квадрата напряжения и ёмкости, для дросселя – от величины электрического тока и индуктивности. Узнав период единственного колебания, эту цифру легко привязать к мощности, как выполняемой работе в единицу времени.
В результате инженер сумеет сказать приблизительно, какого размера ёмкость требуется в конкретном случае. Расчёт ведётся изначально по энергии заряженного конденсатора.
Аналогичное происходит в любой цепи. Конденсаторы служат для фильтрации и гальванической развязки, обязаны легко пропускать нужную частоту и оставаться ёмкими, чтобы не стать бутылочным горлышком в системе.
Величина энергии
Как будет вычисляться накопленный энергетический потенциал, разобраться можно с помощью показанного на снимке блока фотовспышки. Следует напомнить о том, что для увеличения емкости применяют параллельное соединение (Cобщ = C1 + C2 +…+ Cn). При последовательном варианте пропорциональная зависимость обратная (1/Cобщ = 1/C1 + 1/C2 +…+ 1/Cn).
Расчет:
- 2 емкости по 400 мкФ (Cобщ = C1 + C2 = 400 + 400 = 800 мкФ);
- источник питания будет заряжать элемент напряжением 300 В;
- энергия конденсатора W = ½ *C * U2 = ½ * 800 * 10-6 * 300 = 0,12 джоуля.
Использование конденсаторов
Подученное соотношение величин характерно для всех типов конденсаторов. Его используют для того, чтобы определить накопленную энергию при подключении к источнику питания. Измерить напряжение на выводах можно с помощью мультиметра. Кроме емкости, на корпусе конденсатора указывают другие важные параметры:
- рабочий ток;
- номинальное напряжение;
- диэлектрический материал;
- тип элемента.
К сведению. На миниатюрных деталях места для размещения всех данных недостаточно. Применяют систему сокращенных кодировок. Необходимые сведения уточняют в сопроводительной документации либо на официальном сайте производителя.
В следующем перечне приведены примеры электротехнических схем и устройств, которые создают с применением конденсаторов:
- частотный (сглаживающий) фильтр;
- колебательный контур;
- накопитель энергии для формирования мощного импульса (лазер, фотовспышка);
- ограничитель силы тока (компенсатор подключаемой реактивной нагрузки);
- измерение перемещений (изменение емкости при сближении/ отдалении обкладок).
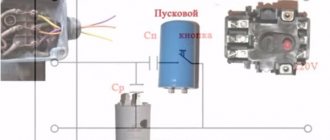
Для автоматизированного расчета типовой схемы можно использовать специализированный калькулятор онлайн. Следующий пример демонстрирует расчет корректного подключения электродвигателя:
- соединение обмоток – треугольник;
- мощность потребления – 1 200 Вт;
- напряжения сети – 220 В;
- cos ϕ – 0,9;
- КПД – 85%;
- емкость рабочего (пускового) конденсатора – 52 (130) мкФ.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.