Продолжаем обсуждение катушек индуктивности, в первой части (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье. И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Расчёт конденсаторов
В общем случае емкостной показатель С определяется по формуле:
C=q/U,
где q – заряд конденсатора на одной из его пластин, U – значение напряжения на конденсаторе.
Из этого выражения можно вывести формулу заряда конденсатора, величину которого можно найти, измерив два других показателя с помощью мультиметра.
Часто возникает вопрос, может ли этот параметр измениться. Он является постоянной величиной, присущей данному элементу и зависящей от его габаритов и устройства. Узнать емкостное значение можно с помощью мультиметра. Пользуясь этими данными, можно рассчитать целевую индуктивность дросселя для колебательного контура или параметры резистора.
В чем измеряется емкость? За измерительную единицу принимается параметр конденсаторного устройства, который можно зарядить 1 Кл до состояния, когда разница потенциалов будет равной 1 вольту. Название этой единицы – фарад (Ф).
Важно! Если сравнить два устройства, идентичных по габаритам, но различающихся тем, что у одного в зазоре между пластинами находится диэлектрический материал, а у другого – воздушное пространство, то при помещении одинаковых зарядов потенциальная разница первой детали будет в Е раз больше. Е – это число, равное диэлектрической проницаемости материала, из которого состоит использованный слой. Ниже приведены формулы для конденсаторных элементов разной конфигурации
Рассчитанные по ним значения соответствуют идеальным устройствам, но релевантны и для реальных в тех случаях, когда емкостными потерями можно пренебречь
Ниже приведены формулы для конденсаторных элементов разной конфигурации. Рассчитанные по ним значения соответствуют идеальным устройствам, но релевантны и для реальных в тех случаях, когда емкостными потерями можно пренебречь.
Формула электрической емкости плоского конденсатора
В основном электрополе пластин плоского конденсатора бывает однородным, за исключением боковых частей, влиянием которых обычно принято пренебрегать. Однако, если пространство между обкладками велико в сопоставлении с их габаритами, краевые искажения нужно учитывать. В общем случае, чтобы высчитать, сколько фарад составит емкость плоского конденсатора, пользуются выражением:
Последовательное и параллельное соединение сопротивлений
C=E*E0*S/d, где S – площадь меньшей обкладки, E0 – электрическая константа, d – длина пространства между пластинами.
Формула электрической емкости цилиндрического изделия
Такой компонент состоит из пары разных по размеру коаксиальных цилиндрических элементов проводника, в пространстве между которыми расположили диэлектрический материал. В этом случае для нахождения емкостной величины не нужно узнавать значение заряда на обкладках конденсатора. Можно воспользоваться следующей формулой емкости:
С=2 π *E*E0*l / ln(R2/R1).
Здесь R1 и R2 – радиусы, соответственно, внутреннего и наружного цилиндров, l – их высота (она одинакова, в то время как радиальные параметры отличаются).
Цилиндрическое изделие
Формула для сферического изделия
Сферическая деталь состоит из двух проводниковых сфер с диэлектрическим слоем между ними. Вот как найти емкость круглого конденсатора:
C=4 π *E*E0* R1* R2 / R2 – R1.
Буквами R обозначены, как и в предыдущем примере, радиусы компонентов.
Ёмкость одиночного проводника
Это характеристика способности твердого проводникового компонента к удержанию электрозаряда. Она определяется особенностями средового окружения (в частности, диэлектрической проницаемостью), взаиморасположением тел, имеющих на себе заряд, размерами детали. От силы тока и величины заряда она не зависит.
Калькулятор соединения резисторов онлайн. параллельное соединение резисторов
Индуктивность
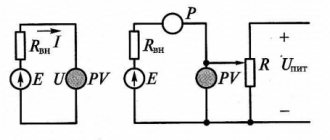
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.
Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
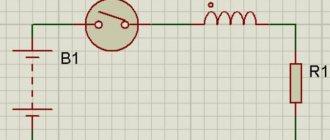
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.
рис 13. Подключение катушки индуктивности к генератору напряжения.
Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Как хорошо сказано в wiki — “При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.”
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
В водопроводной аналогии этому явлению можно сопоставить гидравлический удар, когда масса воды в водопроводе набирает скорость, и при резком закрытии крана вода, продолжая двигаться по инерции, создает высокое давление, что может привести к разрыву трубы.
Причины по которой индуктивность имеет такие свойства (поддержание тока в цепи) хорошо описаны в wiki — https://ru.wikipedia.org/wiki/Самоиндукция
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
По отношению к конденсатору , основным отличием индуктивности, если говорить простыми словами, является то, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность наоборот — пропускает постоянный ток и не пропускает переменный.
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.
Рассмотрим цепь на рис. 13 — подключение катушки индуктивности к генератору напряжения. Ниже представлен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.
рис. 14 График тока в индуктивности при подаче на нее постоянного напряжения.
При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?
рис 15. Подключение индуктивности к генератору тока.
Ну тут из серии «кто кого заборет — слон или кит».
Попробуйте проанализировать работу схемы (hint — вообще схема изображена с ошибкой. В чем она заключается? Как нарисовать схему правильно?)
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16
рис 16. Параллельное включение конденсатора и катушки индуктивности.
Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
В первый момент после замыкания ключа ток в цепи будет равен 0, так как индуктивность препятствует изменению тока. К вагонетке приложили силу, но в первый момент времени ее скорость равна 0. Затем ток начинает возрастать (вагонетка разгоняется). Пружина разжимается все больше и больше, скорость вагонетки (ток) растет и в какой-то момент времени пружина оказывается не сжата. Конденсатор разрядился до 0. Но. Мы помним что «ток в индуктивности мгновенно остановить нельзя!» Вагонетка разогналась и даже если мы не будем ее толкать, она будет двигаться по инерции. То есть индуктивность будет поддерживать ток и при этом заряжать конденсатор, но уже в другой полярности — заряды теперь будут скапливаться на другой обкладке конденсатора. Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю. Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD. Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13? Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи. Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением). В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.
рис 17. Подключение катушки индуктивности к генератору напряжения с учетом внутреннего сопротивления.
На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
В этом случае процесс разворачивается следующим образом. При замыкании ключа S4 цепь замкнется и должен был бы пойти ток. Однако, катушка индуктивности препятствует изменению тока, и в первый момент времени после замыкания ключа ток останется равным 0! По сути дела катушка в этот момент представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке целиком. Можно и по другому подойти — Ur=I*R. Падение напряжения на резисторе равно I*R, I у нас равен 0, поэтому напряжение на резисторе тоже равно 0, и к катушке будет приложено полное напряжение U. Дальше ток в катушке будет расти. В области 0 линейно кстати (см рис 19 «Переход Суворова через Альпы» «Экспонента проходит через 0 под углом 45 градусов»). Ток будет расти и падение напряжения на резисторе тоже будет расти. А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.
Рис. 18 Экспоненциальный график роста тока в индуктивности. ис 19 «Экспонента проходит через 0 под углом 45 градусов»
зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься. «Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.» Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1) где: VL – напряжение (обратная ЭДС), индуцированная на катушке; L – индуктивность катушки; di/dt – скорость изменения тока во времени.
Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол. «ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.
Рис.20 Переходной процесс в цепи с индуктивностью
Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь
Рис.21 Цепь с индуктивностью и переключателем
Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило: Ток в индуктивности в первый момент времени после переключения сохраняется неизменным. Дальше применять закон Ома.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Как найти общее сопротивление при смешанном соединении
Величина М, называемаякоэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
Последовательное соединение катушек индуктивности.
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек — начало второй катушки подключается к концу первой. А второй вариант называют встречным включением — конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом «*«. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M — взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу — уменьшается на ту же самую величину.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Разбирая примеры включения катушек в различные цепи, мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давайте разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = \frac{X_L}{R}
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Таким образом активное сопротивление катушки мы рассмотрели, перейдем к следующему вопросу.
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства . Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2
на
3
и
47 Ом
и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно
учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на
100 Ом
и мощностью
1 Вт
. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А
), а сопротивление каждого из них равно
50 Ом
, тогда мощность рассеивания каждого из них должна быть не менее
0,5 Вт
. В результате на каждом из них выделится по
0,5 Вт
мощности. В сумме это и будет тот самый
1 Вт
.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Параллельное соединение резисторов, наряду с последовательным, является основным способом соединения элементов в электрической цепи. Во втором варианте все элементы установлены последовательно: конец одного элемента соединен с началом следующего. В такой схеме сила тока на всех элементах одинаковая, а падение напряжений зависит от сопротивления каждого элемента. В последовательном соединении есть два узла. К одному подсоединены начала всех элементов, а ко второму их концы. Условно для постоянного тока можно обозначить их как плюс и минус, а для переменного как фазу и ноль. Благодаря своим особенностям находит широкое применение в электрических схемах, в том числе и со смешанным соединением. Свойства одинаковы для постоянного и переменного тока.
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Последовательное соединение проводников
Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.
Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки. Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.
При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.
Watch this video on YouTube
Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.
В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R12R345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
1.3. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ АКТИВНОГО СОПРОТИВЛЕНИЯ R, КОНДЕНСАТОРА С И ИНДУКТИВНОСТИ L
Рассмотрим цепь с активным, индуктивным и емкостным сопротивлениями, включенными последовательно (рис. 1.3.1).
Для анализа схемы разложим напряжение сети U на три составляющие: UR — падение напряжения на активном сопротивлении, UL — падение напряжения на индуктивном сопротивлении, UC — падение напряжения на емкостном сопротивлении.
Ток в цепи I будет общим для всех элементов:
Проверку производят по формуле:
Следует отметить, что напряжения на отдельных участках цепи не всегда совпадают по фазе с током I. Так, на активном сопротивлении падение напряжения совпадает по фазе с током, на индуктивном оно опережает по фазе ток на 90° и на емкостном — отстает от него на 90°. Графически это можно показать на векторной диаграмме (рис. 1.3.2).
Изображенные выше три вектора падения напряжений можно геометрически сложить в один (рис. 1.3.3).
В таком соединении элементов возможны активно-индуктивный или активно-емкостный характеры нагрузки цепи. Следовательно, фазовый сдвиг имеет как положительный, так и отрицательный знак. Интересным является режим, когда = 0. В этом случае
Такой режим работы схемы называется резонансом напряжений. Полное сопротивление при резонансе напряжений имеет минимальное значение: , и при заданном напряжении U ток I может достигнуть максимального значения. Из условия определим резонансную частоту
Явления резонанса напряжений широко используется в радиотехнике и в отдель-ных промышленных установках.
Катушка индуктивности. Формула индуктивности
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2)
- l = длина катушки в метрах (м)
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны. Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Конвертер величин
1 мГн = 0,001 Г. 1 мкГн = 0,000001 = 10⁻⁶ Гн. 1 нГн = 0,000000001 = 10⁻⁹ Гн. 1 пГн = 0,000000000001 = 10⁻¹² Г. Подробнее о единицах измерения индуктивности.
Индуктивность характеризует способность электрического проводника преобразовывать электрический ток в изменение электрического потенциала в данном проводнике (самоиндукция) и в расположенных рядом проводниках (взаимоиндукция). Индуктивность обычно обозначается символом L в честь русского физика немецкого происхождения Эмилия Христиановича Ленца (Heinrich Lenz).
По определению самоиндукции напряжение v(t)
и ток
i(t)
в катушке индуктивности связаны выражением
На всех соединенных параллельно катушках индуктивности имеется одно и то же напряжение V
. В соответствии с правилом Кирхгофа для тока общий ток
I
равен сумме токов, протекающих через отдельные катушки:
Общая индуктивность Leq соединенных параллельно трех катушек индуктивности, расположенных далеко друг от друга и не имеющих общего магнитного поля равна величине, обратной сумме величин, обратных их индуктивностям:
Или для n
несвязанных катушек индуктивности:
Эта формула для L
eq используется для расчетов в этом калькуляторе. Например, общая индуктивность трех катушек индуктивности 10, 15 and 20 мкГн, соединенных параллельно, будет равна
мкГн.
Отметим, что если одна или несколько величин индуктивности равны нулю, то Leq стремится к нулю. Представьте себе очень короткий прямой проводник, шунтирующий катушку индуктивности — он и будет иметь почти нулевую индуктивность. Отметим также, что невозможно создать схему с нулевой индуктивностью. Если параллельно соединены только две катушки индуктивности, имеем:
или
Эквивалентная индуктивность n
одинаковых соединенных параллельно катушек индуктивности
L
равна
Отметим, что формула для расчета общей индуктивности нескольких катушек индуктивности, соединенных параллельно, используется и для расчета сопротивления группы резисторов, соединенных параллельно.
Отметим также, что для группы из любого количества соединенных параллельно катушек индуктивности эквивалентная индуктивность всегда будет меньше самой малой индуктивности в группе катушек индуктивности, а добавление еще одной катушки всегда будет уменьшать эквивалентную индуктивность группы.
Тороидальные катушки индуктивности в модуле питания принтера
Если индукторы расположены в магнитном поле друг друга, эти формулы работать не будут из-за явления взаимоиндукции (взаимной индукции)
, которое рассматривается в нашем калькуляторе взаимной индукции. Эффект взаимоиндукции может уменьшить или увеличить общую индуктивность катушек в зависимости от того как работает магнитная связь между катушками. Величина взаимной индукции зависит от расстояния между катушками и их ориентации. При этом взаимоиндукция может увеличивать или уменьшать общую индуктивность.
Если несколько катушек индуктивности соединены последовательно
, их эквивалентная индуктивность определяется простым сложением индуктивностей отдельных катушек.
Для n
соединенных последовательно катушек индуктивности имеем
Возможно, вы уже заметили, что катушки индуктивности ведут себя точно так же, как резисторы: если катушки соединены последовательно, их эквивалентные индуктивности всегда будет выше, чем индуктивности отдельных катушек, соединенных последовательно, а при параллельном соединении эквивалентная индуктивность всегда будет меньше индуктивностей отдельных катушек.
Многослойная пакетная спиральная катушка индуктивности в микросхеме и ее упрощенная эквивалентная схема
Зачем соединять катушки последовательно, если можно просто намотать большую катушку индуктивности? Вот один из примеров.
В микроэлектронике для реализации довольно больших индуктивностей на единицу площади интегральной микросхемы используется комбинирование спиральных катушек в нескольких слоях металлизации. Для этой цели используется многослойная пакетная конфигурация катушек индуктивности. Несколько слоев металлизации со спиральными катушками располагают точно один над другим. Катушки соединяют последовательно, чтобы индуктивности складывались для получения одной большой катушки индуктивности. Без такого пакетного расположения при использовании планарной технологии было бы невозможно создать большие индуктивности. Благодаря такому пакетному расположению коэффициент связи катушек k
≈ 1.
В этом калькуляторе мы рассматриваем только идеальные катушки индуктивности. Однако мы живем в реальном мире, где реальные катушки обладают как активным сопротивлением, так и емкостью. В другом калькуляторе мы рассмотрим характеристики неидеальных катушек индуктивности, обладающих сопротивлением, которые описываются эквивалентной схемой из последовательно соединенных индуктивности и сопротивления, в частности их временные характеристики.
Бескаркасные катушки индуктивности без сердечников в радиочастотном модуле
Автор статьи: Анатолий Золотков
Электрические цепи. Последовательное и параллельное соединения проводников
Подробности
«Физика – 10 класс»
Как выглядит зависимость силы тока в проводнике от напряжения на нём? Как выглядит зависимость силы тока в проводнике от его сопротивления?
От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и др. Для этого составляют электрические цепи
различной сложности.
К наиболее простым и часто встречающимся соединениям проводников относятся последовательное и параллельное соединения.
Последовательное соединение проводников.
При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочерёдно друг за другом. На рисунке (15.5, а) показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R1 и R2. Это могут быть две лампы, две обмотки электродвигателя и др.
Сила тока в обоих проводниках одинакова, т. е.
I1 = I2 = I. (15.5)
В проводниках электрический заряд в случае постоянного тока не накапливается, и через любое поперечное сечение проводника за определённое время проходит один и тот же заряд.
Напряжение на концах рассматриваемого участка цепи складывается из напряжений на первом и втором проводниках:
U = U1 + U2.
Применяя закон Ома для всего участка в целом и для участков с сопротивлениями проводников R1 и R2, можно доказать, что полное сопротивление всего участка цепи при последовательном соединении равно:
R = R1 + R2. (15.6)
Это правило можно применить для любого числа последовательно соединённых проводников.
Напряжения на проводниках и их сопротивления при последовательном соединении связаны соотношением
Параллельное соединение проводников.
На рисунке (15.5, б) показано параллельное соединение двух проводников 1 и 2 сопротивлениями R1 и R2. В этом случае электрический ток I разветвляется на две части. Силу тока в первом и втором проводниках обозначим через I1 и I2.
Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не накапливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно,
I = I1 + I2. (15.8)
Напряжение U на концах проводников, соединённых параллельно, одинаково, так как они присоединены к одним и тем же точкам цепи.
В осветительной сети обычно поддерживается напряжение 220 В. На это напряжение рассчитаны приборы, потребляющие электрическую энергию. Поэтому параллельное соединение — самый распространённый способ соединения различных потребителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размыкает цепь. Применяя закон Ома для всего участка в целом и для участков проводников сопротивлениями R1 и R2, можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных проводников:
Отсюда следует, что для двух проводников
Напряжения на параллельно соединённых проводниках равны: I1R1 = I2R2. Следовательно,
Обратим внимание на то, что если в какой-то из участков цепи, по которой идёт постоянный ток, параллельно к одному из резисторов подключить конденсатор, то ток через конденсатор не будет идти, цепь на участке с конденсатором будет разомкнута. Однако между обкладками конденсатора будет напряжение, равное напряжению на резисторе, и на обкладках накопится заряд q = CU
Рассмотрим цепочку сопротивлений R — 2R, называемую матрицей (рис. 15.6).
На последнем (правом) звене матрицы напряжение делится пополам из-за равенства сопротивлений, на предыдущем звене напряжение тоже делится пополам, поскольку оно распределяется между резистором сопротивлением R и двумя параллельными резисторами сопротивлениями 2R и т. д. Эта идея — деления напряжения — лежит в основе преобразования двоичного кода в постоянное напряжение, что необходимо для работы компьютеров.
Следующая страница «Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников»»
Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»
Законы постоянного тока – Физика, учебник для 10 класса – Класс!ная физика
Электрический ток. Сила тока — Закон Ома для участка цепи. Сопротивление — Электрические цепи. Последовательное и параллельное соединения проводников — Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» — Работа и мощность постоянного тока — Электродвижущая сила — Закон Ома для полной цепи — Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC..
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC..=Umaxcos.ωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcos.ωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsin.ωt=CUmaxcos.(ωt+π2..)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2.. (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω..=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC..
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C..=LI2max2..
Отсюда:
LC=q2maxI2max..
√LC=qmaxImax..
T=2π√LC=2πqmaxImax..=2·3,1410−610−3..≈6,3·10−3 (с)