Loop Inductance - Theory
Inductance is an idealized element whose properties are similar to an inductive coil, in which the energy of a magnetic field is accumulated.
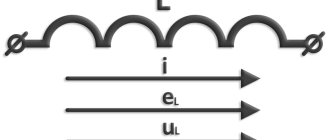
Symbol of inductance and positive directions of current, EMF of self-induction and voltage:
If a current is passed through a conductor, a magnetic flux Φ is created around it. The total magnetic flux (clutch flux) of the inductor is equal to Ψ= w×Φ, where Φ is the magnetic flux created by one turn; w is the number of turns.
By definition, self-inductance (or simply inductance) is equal to the proportionality coefficient between flux linkage and coil current L=Ψ/i.
Inductance is measured in Henry 1 H = 1 Wb / 1 A. The symbol L used to denote inductance was adopted in honor of Heinrich Friedrich Emil Lenz. The unit of inductance is named after Joseph Henry. The term inductance itself was coined by Oliver Heaviside in February 1886.
The coupling flux of the inductor is Ψ=L×i.
In accordance with the law of electromagnetic induction, when the magnetic flux changes in the coil, a self-inductive emf eL=-dΨ/dt is induced. The “-” sign is placed because the EMF has such a direction that the current it generates with its magnetic field prevents the change in the magnetic flux that causes this EMF.
The voltage across the inductance balances the EMF and can be written as uL=-eL=dΨ/dt=L×di/dt.
The instantaneous power entering the inductor is equal to p=uL×i=L×i×di/dt.
The energy stored in the inductor is wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Mutual inductance characterizes the property of one element with current i1 to create a magnetic field that partially meshes with the turns w2 of another element.
The coefficient of mutual inductance is determined by the formula M=Ψ12/i2=Ψ21/i1, where Ψ12 is the coupling flux of the first circuit caused by the current of the second circuit (similar to Ψ21). Measured in Gn.
Electromagnetic induction
Electromagnetic induction is the phenomenon of the occurrence of current in a closed conducting circuit when the magnetic flux passing through it changes.
The phenomenon of electromagnetic induction was discovered by Michael Faraday through a series of experiments.
Experience once. Two coils were wound on one non-conducting base in such a way that the turns of one coil were located between the turns of the second. The turns of the first coil were closed to a galvanometer, and the second were connected to a current source.
When the key was closed and current flowed through the second coil, a current pulse arose in the first. When the switch was opened, a current pulse was also observed, but the current through the galvanometer flowed in the opposite direction.
Experience two. The first coil was connected to a current source, and the second to a galvanometer. In this case, the second coil moved relative to the first. As the coil approached or moved away, the current was recorded.
Experience three. The coil was connected to a galvanometer, and the magnet was moved relative to the coil.
Here's what these experiments showed:
- Induction current occurs only when the lines of magnetic induction change.
- The direction of the current differs when the number of lines increases and when they decrease.
- The strength of the induction current depends on the rate of change of the magnetic flux. In this case, both the field itself can change and the circuit can move in a non-uniform magnetic field.
Why does induced current occur?
Current in a circuit can exist when external forces act on free charges. The work done by these forces to move a single positive charge along a closed loop is equal to electromotive force (EMF).
This means that when the number of magnetic lines through the surface limited by the contour changes, an emf appears in it, which is called the induced emf.
Conductor in an electric field
By placing a conductor in an electric field, the charge carriers inside the conductor begin to move. Moreover, this movement is subject to two rules:
- The electric field strength inside the conductor must be zero
This means that the potential inside the conductor remains constant (φ = const).
- The field strength on the surface of a conductor is directed perpendicular to the very surface of this conductor. Or in other words, the surface of the conductor becomes equipotential , that is, all points on a given surface have the same potential.
From these two rules it follows that when a conductor is brought into an electric field, its charge carriers (in metals these are electrons, and in liquids - ions) begin to move, with positive ones in the direction of the electric field strength, and negative ones in the opposite direction. The result of the movement of charges in a conductor is the appearance of charges of the opposite sign at the ends of the conductor; such charges are called induced . The redistribution of charge in a conductor is shown in the figure below
Distribution of charge carriers of a conductor in an electric field.
Thus, a neutral conductor placed in an electric field seems to break some of the electric field lines, and the induced charges are distributed over the surface of the conductor.
The following situation is of practical interest, when there is some cavity inside the conductor. Since the induction of charges occurs on the surface of the conductor, then inside this conductor, and therefore in the internal cavity, the electric field becomes zero. Electrostatic protection is based on this phenomenon; when it is necessary to protect a device from the effects of an electric field, it is placed inside a shield made of a conductor. Induced charges on the screen surface compensate for the electrostatic field. Instead of a solid screen, a screen made of an electrically conductive mesh is often used, which also makes it possible to create protection from an electrostatic field.
How to find loop inductance
The formula, which is the simplest for finding the value, is the following:
- L=F:I,
where F is the magnetic flux, I is the current in the circuit.
Self-inductive emf can be expressed through inductance:
- Ei = -L x dI : dt.
The formula suggests a conclusion about the numerical equality of induction with EMF, which occurs in the circuit when the current changes by one ammeter in one second.
Variable inductance makes it possible to find the energy of the magnetic field:
- W = L I2 : 2.
Necessary formulas for calculations
To find the inductance of the solenoid, the following formula is applied:
- L= µ0n2V,
where µ0 shows the magnetic permeability of the vacuum, n is the number of turns, V is the volume of the solenoid.
You can also calculate the inductance of the solenoid using another formula:
- L = µ0N2S : l,
It will be interesting➡ The gimlet rule
where S is the cross-sectional area and l is the length of the solenoid.
To find the inductance of the solenoid, any formula is used that is suitable for solving the given problem.
Designation and units of measurement
Current resistance: formula
In honor of Lenz, the unit of inductance was designated by the symbol "L". Expressed as Henry, abbreviated as Gn (in English literature N), in honor of the famous American physicist.
Joseph Henry
If, with a current change of one ampere for every second, the self-inductive emf is 1 volt, then the inductance of the circuit will be measured in 1 henry.
How can inductance be designated in other systems:
- In the SGS system, SGSM - in centimeters. To distinguish it from the unit of length, it is designated abhenry;
- In the SGSE system - in StatHenry.
Content
- 1 Questions and tasks
- 2 Microexperience
- 3 It’s interesting that...
- 4 What to read in “Kvant” about capacitance and inductance
- 5 Answers 5.1 Microexperience
Essentially, Volta and Lenz are referring to the devices you are familiar with - a capacitor and a solenoid, the characteristics of which are capacitance and inductance. It is interesting that if the first electric capacitor - the Leyden jar - was born, one might say, not on purpose, then the solenoid was “discovered” by Ampere in the course of targeted experiments to study the magnetic action of electric current. The units of measurement of capacitance and inductance subsequently received the names Faraday and Henry, by which, presumably, physicists not only paid tribute to the famous scientists, but also emphasized the importance of these concepts.
Of course, separate issues of Kaleidoscope could be devoted to both capacitance and inductance. But the history of science decreed that they had to “work” hand in hand. As soon as it became clear that the discharge of the Leyden jar, and then the induction coil, is oscillatory in nature, a whole galaxy of prominent physicists joined in the study of the oscillatory circuit - Helmholtz, Thomson (Lord Kelvin), Kirchhoff, etc. This “offensive” on the oscillatory circuit was crowned with the discovery Hertz of electromagnetic waves, which ushered in the era of radio and television. No matter what area of electrical, radio and television technology we become interested in today, we will everywhere find either the capacitors and coils themselves, or “echoes” of their presence in more advanced devices. This happens wherever alternating currents and electrical oscillatory processes occur.
Properties
Has the following properties:
- Depends on the number of turns of the circuit, its geometric dimensions and the magnetic properties of the core;
- Cannot be negative;
- Based on the definition, the rate of change of current in the circuit is limited by the value of its inductance;
- As the frequency of the current increases, the reactance of the coil increases;
- It has the property of storing energy - when the current is turned off, the stored energy tends to compensate for the drop in current.
Inductance and capacitor
The current-carrying elements of the device are capable of creating its own inductance. These are such structural parts as masonry, connecting busbars, down conductors, terminals and fuses. It is possible to create additional capacitor inductance by connecting busbars. The operating mode of an electrical circuit depends on inductance, capacitance and active resistance. The formula for calculating the inductance that occurs when approaching the resonant frequency is as follows:
- Ce = C: (1 – 4Π2f2LC),
where Ce determines the effective capacitance of the capacitor, C indicates the actual capacitance, f is the frequency, L is the inductance.
The inductance value must always be taken into account when working with power capacitors. For pulse capacitors, the most important value is the self-inductance. Their discharge falls on the inductive circuit and has two types - aperiodic and oscillatory.
The inductance in a capacitor depends on the connection diagram of the elements in it. For example, when sections and buses are connected in parallel, this value is equal to the sum of the inductances of the package of main buses and terminals. To find this kind of inductance, the formula is as follows:
- Lk = Lp + Lm + Lb,
where Lk shows the inductance of the device, Lp of the package, Lm of the main buses, and Lb of the inductance of the terminals.
If, in a parallel connection, the bus current varies along its length, then the equivalent inductance is determined as follows:
- Lk = Lc : n + µ0 l x d : (3b) + Lb,
where l is the length of the tires, b is its width, and d is the distance between the tires.
To reduce the inductance of the device, it is necessary to arrange the current-carrying parts of the capacitor so that their magnetic fields are mutually compensated. In other words, current-carrying parts with the same current movement must be removed from each other as far as possible, and those with the opposite direction should be brought closer together. By combining down conductors with a decrease in dielectric thickness, the inductance of the section can be reduced. This can also be achieved by dividing one section with a large volume into several with smaller capacity.
Variable capacitors
Initially, people had enough of the capacitors described above from a pair of plates. Then this device was developed. Devices in the form of balls, disks and cylinders began to appear. This was necessary in order to increase the capacitance of the capacitor C, because it is primarily related to the area of the plates S and the distance between them d. This is clearly seen from the formula. It is used to calculate the capacitance of the capacitor.
Capacitor capacity
Over time, these non-standard geometric shapes ceased to satisfy the needs of experimenters. Therefore, new devices with variable capacity were developed. They have movable plates. This allows you to easily change the area of their mutual intersection, thereby affecting the value of the capacitance of the capacitor. The most common and familiar example of this electronic device is the oscillatory circuit in the radio. All people have adjusted the receiver at least once. It is this “twist” that is a variable capacitor. When it rotates, the capacitance changes, and accordingly, the resonant frequency of the oscillatory circuit of the radio receiver changes. This in turn tunes the radio to a different station.
Appearance of a variable capacitor
"Spool of thread"
An inductor is an insulated copper wire wound on a solid base. As for insulation, the choice of material is wide - varnish, wire insulation, and fabric. The magnitude of the magnetic flux depends on the area of the cylinder. If you increase the current in the coil, the magnetic field will become larger and vice versa.
If you apply an electric current to a coil, a voltage appears in it opposite to the current voltage, but it suddenly disappears. This kind of voltage is called electromotive force of self-induction. At the moment the voltage is turned on to the coil, the current changes its value from 0 to a certain number. The voltage at this moment also changes its value, according to Ohm’s law:
- I = U : R,
where I characterizes the current strength, U indicates the voltage, R is the coil resistance.
Another special feature of the coil is the following fact: if you open the “coil - current source” circuit, the EMF will be added to the voltage. The current will also initially increase and then decline. This implies the first law of commutation, which states that the current strength in the inductor does not change instantly.
The coil can be divided into two types:
- With magnetic tip. The material of the heart is ferrites and iron. The cores serve to increase inductance.
- With non-magnetic. Used in cases where the inductance is no more than five milliHenry.
The devices differ in appearance and internal structure. Depending on these parameters, the inductance of the coil is determined. The formula is different in each case. For example, for a single-layer coil the inductance will be equal to:
- L = 10µ0ΠN2R2 : 9R + 10l.
But for a multilayer one there is another formula:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Main conclusions related to the operation of coils:
- On a cylindrical ferrite, the largest inductance occurs in the middle.
- To obtain maximum inductance, it is necessary to wind the turns closely on the coil.
- The smaller the number of turns, the smaller the inductance.
- In a toroidal core, the distance between the turns does not play the role of the coil.
- The inductance value depends on the “turns squared”.
- If inductances are connected in series, then their total value is equal to the sum of the inductances.
- When connecting in parallel, you need to ensure that the inductances are spaced apart on the board. Otherwise, their readings will be incorrect due to the mutual influence of magnetic fields.
It will be interesting➡ Total resistance
About the use of ceramic capacitors...
Fig. 13. – from [11], p.24. “For other types of ceramics, such as Y5U or Y5V, the Z value corresponding to resonance is obtained at significantly lower frequencies, which indicates the worse properties of capacitors with such dielectrics.”
– [10], p.145.
The ESL value does not depend on time, temperature, and frequency (or this dependence is negligible).
2.1.3. Comparison of EC and CC.
As noted above, not all parameters important for the development of modern motherboards are indicated in the documentation of capacitor manufacturers. Therefore, we will use data from Intel Corporation, which used the following parameters when modeling the basic (reference) MV design for the I845G chipset:
Table 3.
| Capacitor, capacity | ESR | ESL | Note |
| OSCON, 560 µF | 9.28 mOhm, max | 6.4 nH, max | 1 |
| Aluminum EC 3300 µF | 12 mOhm | 5 nH | 1 |
| MLCC, 1206 package, 10 µF | 3.5 mOhm, typ. | 1.15 nH, typ. | 1 |
Note 1 to table.
3 – ESR and ESL values are based on values used by Intel to model power distribution and are not manufacturer specifications. – [7], p.66. From tab. Figure 3 shows that high-capacity CCs have several times lower parasitic ESR and ESL than those of ECs. In addition, the much smaller overall dimensions of the CC make it possible to use several tens of CC in parallel, which leads to a corresponding reduction in ESR and ESL. However, the significantly lower capacity of the CC does not allow one to do without the EC completely.
2.2. Operating conditions of capacitors in the power supply circuits of the processor core.
The main assumption made by the author in further presentation is that the physical essence of the effects in the power circuits from the output inductor of the converter to the microprocessor chip is the same for any of the relatively old processors from Intel Pentium-III to Intel Core Duo. The differences are only in the quantitative characteristics and the degree of influence of these effects on the performance and durability of electrolytic capacitors and the processor. These differences are due to the fact that for newer processors: a) the average and maximum current consumption is higher, which increases ohmic losses on the parasitic resistances of the power supply components, motherboard conductors, and processor socket contacts; b) the speed of transient processes on the power buses is higher, which causes increased surges and voltage sags on the parasitic inductances of the power supply components, the conductive paths of the system board, and the contacts of the processor socket; c) the rated supply voltage of the processor core is lower, which reduces the noise immunity margin - this forces stricter requirements for supply voltage stability and resistance to the destabilizing factors listed above. With this in mind, we will try to analyze the documentation for processors in the specified “range”.
2.3. Requirements for power circuits. Let's try to find out why and what requirements the processor manufacturer places on power supply circuits and PWM converters. We will rely on documentation from INTEL, as a manufacturer of the highest-frequency processors for which the effects under study can be of greatest importance.
“Due to the very large number of transistors and the high internal clock frequency, the processor is capable of producing large fluctuations in average current between low and full load states.”
— [12], p.19.
“The inevitable inductance of power wires and rails reduces the power supply's ability to respond quickly to current transients.
Blocking (Decoupling) of power buses can be characterized by several features [in the original - “areas of interest”].
The closer the capacitors are located to the load, the more inductance will be bypassed.
To bypass soldering inductances, power buses, etc. Less capacity required. Thus, the proximity [of capacitors] to the load [requires] less space to accommodate them. <…> The converter's feedback loop response time is much longer than the time it takes for a change in processor load to cause a [transient] effect. This is especially true if the load change occurs at a high rate. A battery of [electrolytic] capacitors supplies energy to the depleted high frequency blocking [ceramic] capacitors until the power supply can respond. Rather, the bank of [electrolytic] capacitors reduces the transient requirements of the power supply to values that it can provide. <…> High-frequency [ceramic] blocking capacitors should be located as close to the processor power pins as physically possible. This is a vital requirement, because... The inductance of the power rails on the board can negate the benefits of using these low-inductance components." — [13], pp. 33,34.
“For example, <…> 250 picoHenry of [stray] inductance is typically ignored in power distribution systems until the 1 A/ns current swings that occur with a Pentium-III processor occur.
The voltage drop across the inductance in this case can be 250 mV.” — [14], page 9.
“The zone <...> PWM regulation <...> is defined as the frequency band of the controller with a closed feedback circuit.
A typical value is 30-40 kHz for a 300 kHz regulator." — [15], p. 26.
“A typical converter has a response time ranging from 1 to 100 μs, while differences in processor current consumption take from 1 to 20 ns”
— [14], p. 19.
(Please note how high the rate of change in current was for slotted 500 MHz (!) processors in 1999! Apparently, it was meant that for these processors such a speed would have been achieved in the absence of blocking ceramic capacitors near the processor chip.) Read on ibid: “For Pentium-III, current drops caused by load changes can be 15.3 A or higher.
These are not only rapid changes in current consumption, but also long periods of average current consumption. Note that even during normal operations, current requirements may vary by 7 A or more due to changes in the active levels of on-chip logic gates (components).” — [14], p.19.
A jump in current consumption of seven or more amperes in one or several nanoseconds cannot be achieved without blocking ceramic capacitors directly next to the processor chip, because the current through the power buses simply does not have time to increase due to the parasitic inductance of the conductors, which is significant at such speeds. Thus, the author has the opinion that ceramic capacitors near the socket and directly on the processor act as energy storage devices, which they provide to the processor core until the current through the parasitic inductances increases to the required value. Unfortunately, there is no complete certainty on this issue, partly because of the position. Here is how the concepts of “ripple” and “noise” were defined: “Output ripple and noise are defined as a periodic or random signal in the frequency range up to 20 MHz at the output of the [power supply] under
constant load .
(Highlighted and underlined by me - Ya.M.)" - [6], p. 14. That is. Current drops due to changes
in processor load do not fall under this definition.
Intel's terminology subsequently changed, actually contradicting the quoted definition: "The output filter contains high-frequency blocking [ceramic] capacitors to ensure the suppression of ripple and chassis noise to certain levels."
– [16], p. 35. Most likely, according to the author, this is due to the fact that in the recommendations of recent years for developers, instead of formulas and examples of calculations, specific numerical values are given (quantity, denomination, maximum permissible ESR and ESL, location for electrolytic and ceramic capacitors), accordingly, there is no need for a detailed consideration of the physical processes on the power buses.
“Due to the fact that electrolytic blocking capacitors have not only ESR, but also quite high inductance, these capacitors need the help of other capacitors that have lower inductance (but also, usually, lower capacitance).
These high-frequency [ceramic] capacitors control the switching edges and support the power rails during load changes until the higher-inductance [electrolytic] capacitors can respond." - [14], page 22 - this explanation from 1999 more meaningfully reveals the purpose of the CC than simply “guaranteed noise suppression.”
2.4. Model concept.
To a first approximation, the power system model looks like shown in Fig. 14:
Rice. 14. Here: voltage source V1
and inductor
L1
- simulate a step-down converter,
C1
- a battery of electrolytic blocking capacitors installed in close proximity to the output inductor L1,
R1
and
L2
- parasitic ESR and ESL power buses from C1 to C2 (conductors, soldering),
C2
- a battery of ceramic blocking capacitors
near the processor socket
,
R2
and
L3
– total parasitic ESR and ESL of power circuits from C2 to C3 (conductors, solders, connector contacts, legs (pins) of the processor, conductors in the processor case from the pins to the location of C3),
C3
– ceramic blocking battery capacitors
near the processor chip
, located directly
on the processor body
.
The CPU's
programmable current source simulates the current consumption of the processor core.
The operation of the circuit, taking into account the above, can be explained as follows: C3 maintains the supply voltage of the processor core within acceptable limits during consumption surges, until the current from C2 through R2L3 changes accordingly. The main reason for the slow change in current here is the inductance L3. Additionally, C3 suppresses noise and interference from a running processor to a safe level. C2 performs the same role in relation to C3 until the current from C1 through R1L2 changes. The main reason for the slow change in current here is the inductance L2 and the parasitic internal series inductance EC C1, not shown in the diagram. C2 also unloads C1 from high-speed current drops (thereby reducing the power released on it, i.e. reducing the heating of the EC) and further reduces noise and interference. C1 maintains the supply voltage of all subsequent circuits within acceptable limits until the converter responds to a change in current consumption. The main reason for the slow change in current here is the reaction time of the converter to a change in load current. This is well illustrated in Fig. 15:
Fig. 15 – from [17], p.25.
3. Circuit modeling in the Micro-Cap 8 program.
Let’s set ourselves the goal of finding out how the range of supply voltage ripples directly on the processor chip Vcpu and the power dissipated by the EC depend on the number and location of the CC connection.
3.1. Schemes for modeling.
When choosing a circuit for modeling, the author of the article proceeded from the following considerations: a) in most boards for mPGA478, as well as for LGA775, multi-phase PWM converters (2...4-phase) are used;
b) parasitic parameters of copper printed conductors do not significantly depend on the type of processor used. But it’s difficult to take into account the layout of any specific board, incl. and due to the presence of internal layers. At least, if you set the goal only to find out the degree of influence of the capacitance and location of the CC on the heat release in the EC, this part of the circuit can be left unchanged; c) approximate relationships between the parasitic parameters of various processor sockets can be determined from Tables 4 and 5, and when carrying out modeling for a specific socket, the values of the corresponding circuit elements should be changed; d) to simulate the behavior of a circuit with a specific processor, it is necessary to set the parameters of the current drop (for the current source I_PWL) in accordance with the speed and maximum/minimum consumption of a given processor; These parameters are provided in the processor manufacturer's data sheet. Therefore, the scheme proposed in [15], pp. 71-79 was taken as a basis. A modified version of the circuit is presented in Fig. 16. Compared to the original circuit, the value of R1 was changed and the elements simulating the parasitic parameters of the laboratory instrument (external load device and positioner adapter) were removed. Added models of capacitors CDOP1, CDOP2, CCPU1, switches S1...S3, voltage sources V1, V2 and their output chokes LVR1, LVR2. To simulate a board with a single-phase converter for PGA-370, you can use a simplified version of the circuit in Fig. 17. The following disadvantages of the model used should be noted: – both circuits use the simplest 3-element equivalent circuits EC and CC, which do not take into account changes in the main parameters of capacitors with temperature, voltage, frequency; – the circuits do not take into account the limited speed of the PWM converter, so in reality the power allocated to the EC is much higher; – the diagrams do not take into account the parasitic parameters of the connections between
the EC in the battery;
– in real processors, special CCs of smaller capacity with significantly reduced inductance and resistance are located near the crystal, so in reality ripples are suppressed better
than modeling shows.
Fig. 16.
Fig. 17.
3.2. Description of the circuit (Fig. 16).
V1, V2 – constant voltage sources 1.5 V; LVR1 – output inductor (choke) of the first step-down converter (VR1); LVR2 – output choke of the second step-down converter (VR2); CMB1, RMB1, LMB1 – respectively, the total capacitance, effective series resistance (ESR), equivalent series inductance (ESL) of the battery of electrolytic capacitors at the output of VR1; CMB3, RMB3, LMB3 – the same at the VR2 output; CDOP1, RDOP1, LDOP1 – respectively, the total capacitance, ESR, ESL of additional ceramic capacitors soldered to the terminals of electrolytic capacitors at output VR1 (can be turned off with switch S2); CDOP2, RDOP2, LDOP2 – the same for VR2 CMB2, RMB2, LMB2 – respectively, the total capacity, ESR, ESL of batteries of ceramic multilayer capacitors (MLCC) located in close proximity to the processor socket (can be turned off with switch S1); RMB101 and LMB101 – parasitic resistance and inductance of conductors from the output choke VR1 to the socket connection point (from the “north” side); RMB105 and LMB105 – the same for VR2 on the “south” side of the socket; RMB102 and LMB102 – parasitic resistance and inductance of conductors from the socket connection point on the “north” side to the middle of the central cutout in the socket; RMB104 and LMB104 – the same on the “south” side; RMB103 and LMB103 – parasitic resistance and inductance of conductors from the middle of the central cutout in the socket to the connection point on the “south” side of the socket; RSKT1, LSKT1 – parasitic resistance and inductance of the “northern” segment of the socket; RSKT2, LSKT2 – the same for the central segment of the socket; RSKT3, LSKT3 – the same for the “southern” segment of the socket; CCPU1, RCPU1, LCPU1 – respectively, the total capacity, ESR, ESL of ceramic capacitors located directly on the processor (can be turned off with switch S3). Parameters of socket pins and processor pins. Table 4. Inductance.
| Connector | Inductance of one pair of contacts (Lpairs) | Number of Vcc pins (NVcc) | Number of Vss pins (NVss) | Total inductance (Ltotal) | Link to primary sources |
| PGA370 | 3.5 nH | 74 | 74 | 47 pH | [18, 12] |
| mPGA478 | 3.3 nH | 85 | 180 | 29 pH | [19, 20] |
| LGA775 | 3.9 nH | 226 | 273 | 15 pH | [21, 22] |
Table 5. Resistance.
| Connector | Resistance of one pair of contacts (max) (Rpairs) | Number of Vcc pins (NVcc) | Number of Vss pins (NVss) | Total resistance (Rtotal) | Link to primary sources |
| PGA370 | 25 mOhm | 74 | 74 | 0.3 mOhm | [18, 12] |
| mPGA478 | 25 mOhm | 85 | 180 | 0.2 mOhm | [19, 20] |
| LGA775 | 28 mOhm | 226 | 273 | 0.1 mOhm | [21, 22] |
Notes to tab. 4 and 5 : 1. The number of power (Vcc) and ground (Vss) pins may vary slightly depending on the processor model. 2. General inductance and resistance were calculated with subsequent rounding according to the formulas: Ltot. = Lpairs / NVcc / 2 + Lpairs / NVss / 2, Rtot. = Rpairs / NVcc / 2 + Rpairs / NVss / 2.
3.3. Simulation results.
Let's carry out modeling for a configuration consisting of a 2-phase PWM converter and a Pentium-4 3000 MHz processor (see Fig. 16). Let's leave the filter parameters the same (accepted for more powerful processors in the LGA775 package; they should satisfy the needs of the selected processor with a margin). To be able to vary the parameters step by step, we note that the EC batteries (SMV1 and SMV3) are made up of six and four ECs, respectively, with a capacity of 560 μF, ESR = 6 mOhm, ESL = 3.3 nH. Parameters of one CC: C=10 μF, ESR=2.88 mOhm, ESL=1080 pH. For convenience, the parameters of batteries of such capacitors are summarized in Table 6: Table 6.
| C, µF | 10 | 20 | 40 | 60 | 100 |
| ESR, mOhm | 2,88 | 1,44 | 0,72 | 0,48 | 0,288 |
| ESL, pH | 1080 | 540 | 270 | 180 | 108 |
In accordance with Tables 4 and 5, we will increase the parasitic parameters of the socket contacts RSKT1...RSKT3 and LSKT1...LSKT3 by 2 times compared to the original ones corresponding to the LGA775 connector. It remains to resolve the issue with the magnitude and duration of the test current drop. The guidelines for the development of core power converters for the Pentium-3 ([6], p. 14) and Pentium-4 ([23], p. 11 and [17], p. 7) processors show the parameters of current drops in some worst-case circumstances – see Fig. 18 and notes thereto.
Notes to Fig. 18: – The duration of periods of maximum and minimum load depends on the speed of the processor: a faster processor has a shorter duration.
– Other operating system-controlled events may have a rise time of 700 clock cycles. – The worst set of circumstances can force the processor current consumption to cycle through transitions of 100% -> 40% -> 100% in 30-50 clock cycles. Rice.
18 - from [17], p.7. Let's program the current source I_PWL to simulate one swing period, shown at the top of Fig. 18. The expression will look like (in one line): pwl 0,0 0.3u,3.24 0.300333u,25.92 0.301998u,32.4 0.385248u,32.4 0.391908u,64.8 2.591908u,64.8 2.592241u,25.92 2.59 2907u,32.4 2.726107u,32.4 2.72644u,3.24 4.82644u,3.24 1.3,0 Here: pwl - generator type, - programmable constant current source; 0,0 - zero initial values (the number to the left of the decimal point is the moment of time, and to the right is the current value corresponding to this moment), used in order to avoid the “ringing” of the model caused by a current jump at an infinite speed with a non-zero current at the zero moment of time ; 0.3u,3.24 - relatively smooth (over almost 1000 clock cycles) linear increase in the processor current to the minimum value (according to Fig. 18 - 5% of the maximum current, for the selected processor Imax = 64.8 A); 0.300333u,25.92 - jump from 5% to 40% in one clock cycle (1 clock cycle = 0.333 ns = 333 ps); 0.301998u,32.4 — a jump from 40% to 50% in 5 clock cycles (we are considering the worst case scenario, so we choose the smallest value from the “5-10 clock cycles” bracket); 0.385248u,32.4 - current holding for 250 cycles; 0.391908u,64.8 - jump from 50% to 100% in 20 ticks; 2.591908u,64.8 - current holding for 2.2 μs; 2.592241u,25.92 - current decline from 100% to 40% in 1 cycle; 2.592907u,32.4 - current increase from 40% to 50% in 2 cycles; 2.726107u,32.4 - current holding for 400 cycles; 2.72644u,3.24 - current decline from 50% to 5% per 1 clock cycle; 4.82644u,3.24 - current holding for 2.1 μs; 1.3.0 - smooth decrease in current to zero in a gigantic, on the scale of the process under study, time of 1.3 s.
From the documentation for the processor, we find out that the maximum current consumption of the selected processor is 64.8 A. The time of one cycle is 0.333 ns. 3.3.1. Influence of connection location and CC capacity.
Let's open all the switches (Fig. 16). Let's make a “test” battery KK 20 uF with parameters according to Table 6 and connect it alternately to points Vcpu (test 1), Vmlcc (test 2). We will connect to the EC (SMV1 and SMV3) in 3 variants - first, 10 μF (experiment 3), then 20 μF (experiment 4), then we will simulate a situation where a 10 μF CC is soldered to the terminals of each individual EC (experiment 5). The simulation results for each case in the order listed are summarized in Table 7:
Table 7.
| Experience no. | Connection point | Total capacitance CC, µF | Total power dissipated by EC, μW | Ripple range, peak to peak, V |
| 1 | Vcpu | 20 | 4,905 | 0,385 |
| 2 | Vmlcc | 20 | 4,519 | 2,7 |
| 3 | SMV1 and SMV3 | 20 | 8,817 | 2,9 |
| 4 | SMV1 and SMV3 | 40 | 5,485 | 0,068 |
| 5 | SMV1 and SMV3 | 100 | 3,010 | 1,597 |
Notes to tables 7 and 8: – the power dissipated by the EC was calculated as an integral over the analysis time (3.5 μs);
– the ripple amplitude was measured according to the graph constructed by the program, and peaks and dips less than 100 ns wide were ignored - this opportunity was provided by Intel in [15] on page 25; – in table 7 in lines 2, 3 and 5 the ripple range exceeds the supply voltage – there is no typo here, this is exactly what Micro-Cap shows. This is due to the fact that, unlike the real board, we turned off all capacitors in the model in order to determine the most advantageous connection point for the CC. Taking into account the results of experiments 1...3, it can be noted that in this case (i.e. in the absence of other CCs), all other things being equal, the greatest reduction in heat generation in the CC is achieved by connecting a test capacitor near the processor socket. This is where board manufacturers place all QCs. But from the result of experiment 5 it is clear that there is an opportunity to improve the situation. (The sharp decrease in ripple in experiment 4 (Table 7) is apparently associated with an unintentional resonance effect in the model - there is no doubt that the processor will not be able to work without capacitors on the case.) Now let’s determine how the board will behave with the components already mounted filters. To find out this, let's close switches S1 and S3 in our model - thereby we bring our model to a seemingly “ideal” (i.e., standard, recommended by the processor manufacturer) state, and run the simulation again. First, without a “test” capacitor at all (“standard” reference), and then with alternate connections in the order already listed above. The results are in table 8:
Table 8.
| Experience no. | Connection point | Total capacitance CC, µF | Total power dissipated by EC, μW | Ripple range, peak to peak, V |
| Standard | –––– | –––– | 1,009 | 0,12 |
| 1 | Vcpu | 20 | 0,943 | 0,15 |
| 2 | Vmlcc | 20 | 1,196 | 0,1 |
| 3 | SMV1 and SMV3 | 20 | 0,745 | 0,12 |
| 4 | SMV1 and SMV3 | 40 | 0,475 | 0,1 |
| 5 | SMV1 and SMV3 | 100 | 0,357 | 0,1 |
| Check | Vmlcc | 100 | 5,02 | 0,08 |
Interesting situation! This time, the greatest reduction in the released power occurs when the test capacitor is connected directly to the EC, and when connected near the socket, there is even a slight increase in this parameter! But the most interesting thing is in the results of experiments 4 and 5 (Table 8). It follows from them that even if the computer motherboard was designed in full accordance with Intel recommendations, and the manufacturer installed all the CCs on the board (which happens very, very rarely), the heat dissipation on the EC can be reduced by at least 2.8 times! And all costs in this case are the price of the CC in an amount equal to the number of ECs (or the price of a faulty board from which they can be removed). But let's check ourselves - perhaps the effect is caused by a simple increase (by 100 µF) in the total capacitance of the CC in the power circuit? To do this, we disconnect our test capacitors from the EC and connect an additional CC with a capacity of 100 μF to the Vmlcc point (other parameters are in Table 6). For more details, see the supplement to the article. The result is in the bottom line of the table. 8 – allows us to draw the following conclusions.
3.3.2. Conclusions.
Firstly, soldering the CC to the EC terminals is necessary, because really allows you to significantly reduce the power allocated to them (and accordingly increase their durability). Secondly, a reckless increase in the CC capacity near the processor socket beyond that recommended by Intel can lead to the opposite result - the principle “you can’t spoil the porridge with butter” is unacceptable here. Thirdly, if there are too many empty slots around the processor socket on the board for CC in the 1206 case, you should think about soldering them onto some of these places. But the final decision can be made only after you have read the documentation for your processor, found out the number, size and capacity of CC recommended by Intel and made sure that there are clearly not enough of them on your board.
4. Practical recommendations for additional soldering of CC to EC terminals.
One or more CCs with a total capacity of about 10 μF per EC must be soldered to the terminals of each EC standing before and after each inductor of the PWM converter.
4.1.
Preparation. For convenience and safety (in terms of the safety of the system board), you should use small 9 by 4 mm auxiliary boards made of one-sided foil fiberglass with holes in accordance with the distance between the pins of a particular EC. The author used double-sided foiled fiberglass and split it into two single-sided sheets with a sharp knife. The permissible thickness of the workpieces is determined by the length of the protruding part of the EC pins above the surface of the system board; in many cases, a thickness of 0.5 mm will be sufficient. The foil between the holes on the board must be removed (but not all of it! only a narrow strip across the line connecting the holes), the width of the foil cut is 1 mm, the sketch is shown in Fig. 19.
Rice. 19. First we solder the CC onto these boards, then we put the boards on the EC terminals and carefully solder them.
4.2. Carrying out work.
IMPORTANT!!! Before work, all components (processor, memory, expansion cards, cables, batteries, etc.) must be removed from the board.
Attention! If the ECs are in a row and the terminals are all on the same line, make sure that you did not make a mistake and did not put the board on the terminals of different adjacent capacitors. Once again Attention! The boards should be installed with parts and foil OUTSIDE the system board!
Solder with a well-heated low-voltage soldering iron with a tip galvanically connected to the common wire of the system board.
Each soldered CC must be checked for the absence of a short circuit (SC). Each assembled auxiliary board must be checked for short circuits. After soldering is completed on the EC terminals, before power is applied, a check for the absence of a short circuit must be carried out again.
4.3. Switching on and checking.
The procedure is well known, but still briefly about the key points. Only after making sure that there is no short circuit anywhere can you connect the motherboard (without the processor and components!) to the power supply and try to turn it on (watch out for your eyes! Stuff happens...). If there are no fireworks, we check the ratings of all voltages. If everything is in order, turn off the power, install only the processor and speaker, and turn on the power again. If the processor has started and the POST program begins to produce characteristic sound signals due to the lack of RAM, turn off the power and install the remaining components.
5. Additions to the article.
For the convenience of virtual “experimentation” with the model, the diagram has been supplemented. In order not to make changes to the circuit every time, it is better to immediately provide all the necessary options that can be connected using animated switches. This version of the circuit is presented in Fig. 20, and the corresponding circuit file can be downloaded from the link: https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26791&filename=mPGA478_4_5.zip
Fig.20. Chain C10 R112 L112 is connected by switch S8 to perform experiment 1 according to the table. 8. Chain C4 R106 L106 is connected by switch S4 to perform experiment 2 according to the table. 8. Chains C5 R107 L107 and C6 R108 L108 are connected by switch S5 to perform experiment 3 according to the table. 8. Chains C7 R109 L109 and C8 R110 L110 are connected by switch S6 to perform experiment 4 according to the table. 8. Chain C9 R111 L111 is connected by switch S7 to perform the “Test” experiment according to the table. 8.
You can at the conference (this is the address, in Cyrillic)
https://www.rom.by/forum/Electrolytic_capacitors The author of this article is present there under the nickname Ter_Abit.
Circuit files for the Micro-Cap 8 program (compatible with the seventh version of this program) are available for download in a zip archive at the link: https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26654&filename =Ceramic_sch.zip The journal version of the article is available for download at the following links: Part 1 (djvu, 207 kB) - https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26655&filename=Ceramic_1.djvu ; Part 2 (pdf, 169 kB) - https://cp.people.overclockers.ru/cgi-bin/dl.pl?id=26653&filename=rh607_4750.pdf.
The author expresses gratitude to: – the moderators and participants of this conference for a constructive discussion, – A. Sorokin for the impetus to thinking in the right direction contained in his article [1], – S.A. Amelin (Smolensk) for advice and assistance in mastering Micro-Cap.
Literature.
1. Sorokin A. Features of the use of oxide capacitors in power circuits of microprocessors. - Radio, 2003, No. 1, p. 20 2. www.rom.by 3. ALUMINUM ELECTROLYTIC CAPACITORS CAT. No. E1001G (Ver.2). Nippon Chemi-Con. (al-productionguide-e-070315.pdf from the Nippon Chemi-Con website). 4. Aluminum Electrolytic Capacitors General technical information. EPCOS.(PDF_GeneralTechnicalInformation.pdf from the EPCOS website). 5. Aluminum Electrolytic Capacitors 10.2006. SANYO. (EC_E.pdf from SANYO website). 6. VRM 8.5 DC–DC Converter Design Guidelines (24965902.pdf, www.intel.com). 7. Intel® Pentium® 4 Processor in 478-pin Package and Intel® 845G/845GL/845GV Chipset Platform Design Guide (29865402.pdf, www.intel.com). 8. Solid Electrolytic Capacitors with Functional Polymer RE Series R5 Type. FUJITSU. (re-r5e.pdf from FUJITSU website). 9. Multilayer ceramic capacitors. General technical information. October 2006. EPCOS. (PDF_General.pdf from the EPCOS website). 10. Meleshin V. Transistor converter technology. Publishing house "Technosphere", 2005. 11. Multilayer ceramic capacitors. Chip capacitors, Advanced series, C0G and X7R. October 2006 (AS_C0G_X7R_CC.pdf from the EPCOS website). 12. Intel® Pentium® III Processor with 512KB L2 Cache at 1.13GHz to 1.40GHz (24965704.pdf, www.intel.com). 13. Low Voltage Intel® Pentium® III Processor 512K Dual Processor Platform Design Guide (27367401.pdf, www.intel.com). 14. Pentium® III Processor Power Distribution Guidelines Application Note. April 1999. (24508501.pdf, www.intel.com). 15. Voltage Regulator-Down (VRD) 11.0 Processor Power Delivery Design Guidelines For Desktop LGA775 Socket (31321402.pdf, www.intel.com). 16. Voltage Regulator-Down (VRD) 10.1 Design Guide For Desktop LGA775 Socket (30235604.pdf, www.intel.com). 17. Specialty Polymer Aluminum Electrolytic Capacitors. TECHNICAL GUIDE. Panasonic Industrial Company (SP-Cap_2004-technical-guide.pdf, www.panasonic.com). 18. 370-Pin Socket (PGA370) Design Guidelines (24441002.pdf, www.intel.com). 19. Intel® Pentium® 4 Processor 478-Pin Socket (mPGA478) Design Guidelines (24989002.pdf, www.intel.com). 20. Intel® Pentium® 4 Processor with 512-KB L2 Cache on 0.13 Micron Process Datasheet (29864310.pdf, www.intel.com). 21. LGA775 Socket Mechanical Design Guide (30266603.pdf, www.intel.com). 22. Intel® Pentium® 4 Processor 6xx Sequence and Intel® Pentium® 4 Processor Extreme Edition Datasheet (30638203.pdf, www.intel.com). 23. Intel Pentium 4 Processor VR-Down Design Guidelines (24989104.pdf, www.intel.com).
06/24/2006. (c) Yaroslav Malov, otherwise known as Ter_Abit.
Application of inductors
Inductors are widely used in analog and signal processing circuits. They combine with capacitors and other radio components to form special circuits that can amplify or filter signals of a specific frequency.
Inductors have a wide range of applications ranging from large inductors such as power supply chokes that, in combination with filter capacitors, eliminate residual noise and other oscillations in the power supply output, to as small inductors as those found inside integrated circuits.
Two (or more) inductors, which are connected by a single magnetic flux, form a transformer, which is the main component of circuits operating with an electrical power supply network. Transformer efficiency increases with increasing voltage frequency.
For this reason, aircraft use AC voltage with a frequency of 400 hertz instead of the usual 50 or 60 hertz, which in turn allows for significant savings in the mass of transformers used in the aircraft power supply.
Inductors are also used as energy storage devices in switching voltage stabilizers, in high-voltage electrical power transmission systems to deliberately reduce system voltage or limit short-circuit current.
What a capacitor is no longer
One common belief is that the main role of a capacitor is to store charge, much like a bucket of water is filled with one cup while being emptied by another.
If you've ever gotten into a debate about "does current flow through a capacitor" and gone more into politics than physics, you know that typical analogies don't make much sense when it comes to alternating current. A capacitor is simply two conductors separated by a dielectric, and nowhere in the basic physical explanations of its properties will you find an explanation of what to do about it.
Energy storage is just one of the many uses of a capacitor, such as filtering, shaping, and inverting electrical signals and impedances. We tend to think of this as the primary use of a capacitor, as it was its first use in the early days of direct current electricity and William Gilbert's electroscope, invented in the 15th century.
General information
In order to understand what the inductance of the coil depends on, it is necessary to study in detail all the information about this physical quantity. The first step is to consider the accepted international designation of the parameter, its purpose, characteristics and units of measurement.
The very concept of inductance was proposed by the famous English physicist Oliver Heaviside, who studied it. This scientist gave the world other well-known terms - electrical conductivity, magnetic permeability and resistance, as well as EMF (electromotive force).
The first letter of the surname of another famous physicist, Emilia Lenza, was taken as a designation for inductance in formulas and when carrying out calculations. Today, the symbol L continues to be used when referring to this parameter.
The outstanding American physicist Joseph Henry was the first to discover the phenomenon of inductance. In his honor, physicists named the unit of measurement in the international SI, which is most often used in calculations. In other systems (Gaussian and SGS), inductance is measured in centimeters. To simplify the calculations, a relationship was adopted in which 1 cm equals 1 nanohenry. The very rarely used SGSE system leaves the self-induction coefficient without any units of measurement or uses the stathenry value. It depends on several parameters and is approximately equal to 89875520000 henry.
Among the main properties of inductance are:
- The parameter value can never be less than zero.
- The indicator depends only on the magnetic properties of the coil core, as well as on the geometric dimensions of the circuit.
Calculation methods
There are several basic ways to determine the inductance of a coil. All formulas that will be used in the calculations can be easily found in reference books or on the Internet. The whole calculation process is quite simple and will not be difficult for people with basic mathematical and physical knowledge.
Through current
This calculation is considered the simplest way to determine the inductance of a coil. The formula through current follows from the term itself. What is the inductance of the coil can be determined by the formula: L=Ф/I, where:
- L - circuit inductance (in Henry);
- F is the magnitude of the magnetic flux, measured in webers;
- I is the current strength in the coil (in amperes).
This formula is only suitable for a single-turn circuit. If the coil consists of several turns, then instead of the magnetic flux value, the total flux (total value) is used. When the same magnetic flux passes through all the turns, then to determine the total value it is enough to multiply the value of one of them by the total number.
Finite Length Solenoid
The solenoid is a thin long coil, where the thickness of the winding is significantly less than the diameter. In this case, calculations are carried out using the same formula as through current strength, only the magnitude of the magnetic flux will be determined as follows: Ф=µ0NS/l, where:
- µ0 is the magnetic permeability of the medium, determined from lookup tables (for air, which is taken by default in most calculations, it is equal to 0.00000126 henry/meter);
- N is the number of turns in the coil;
- S is the cross-sectional area of the coil, measured in square meters;
- l is the length of the solenoid in meters.
The self-induction coefficient of the solenoid can also be calculated based on the method for determining the energy of the magnetic flux of the field. This is a simpler option, but it requires some quantities. The formula for finding inductance is L=2W/I 2, where:
- W is the magnetic flux energy, measured in joules;
- I is the current strength in amperes.
Toroidal core coil
In most cases, the toroidal coil is wound on a core made of a material with high magnetic permeability. In this case, to calculate the inductance, you can use the formula for a straight solenoid of infinite length. It has the following form: L=N µ0 µS/2 πr, where:
- N is the number of coil turns;
- µ—relative magnetic permeability;
- µ0—magnetic constant;
- S is the cross-sectional area of the core;
- π is a mathematical constant equal to 3.14;
- r is the average radius of the torus.
It will be interesting➡ Types of current sources
Long conductor
Most of these quasi-linear conductors have a circular cross-section. In this case, the value of the self-induction coefficient will be determined by the standard formula for approximate calculations: L= µ0l (µelnl/r+ µi/4)/2 π. The following notations are used here:
- l is the length of the conductor in meters;
- r is the radius of the wire cross-section, measured in meters;
- µ0—magnetic constant;
- µi is the relative magnetic permeability characteristic of the material from which the conductor is made;
- µe is the relative magnetic permeability of the external environment (most often the value for vacuum is taken to be 1);
- π—pi number;
- ln is the notation for logarithm.
How does a capacitor work?
Generally speaking, a capacitor accumulates charge on its plates (many elementary particles, each of which has an elementary charge). The more charge accumulated, the more energy is stored. The capacitance of the capacitor also depends on the type of dielectric.
Two plates separated by a thin layer of air (air is also a dielectric) have a very small capacitance, and in this form capacitors are not used.
With the help of special materials and technological tricks, we learned how to squeeze a fairly large container into a very small volume.
The most typical example is electrolytic capacitors.
In them, two metal plates in the form of long strips (most often made of aluminum foil) are separated by a layer of paper impregnated with electrolyte.
The electrolyte causes the formation of a thin film of oxide (oxide), which is a good dielectric.
Therefore, electrolytic capacitors are also called oxide capacitors. The strips are rolled up and placed in a cylindrical aluminum housing.
Previously, capacitor terminals were made of copper - as a material with high electrical conductivity. Now they are often made from cheaper iron-based alloys. You can verify this by holding a magnet close to them. Business owners have learned to save money!
In ceramic capacitors, the dielectric is a ceramic plate, and the plates are films of metal alloys sprayed onto the ceramic.
Graphical output of the formula
It is possible to obtain the written formula using the graphical method. To do this, let us display on a graph the dependence of the magnetic flux Φ(I) on the current I (Fig. 1.21.2). The total amount of heat released, which is equal to the initial energy reserve of the magnetic field, is determined as the area of the resulting figure in Fig. 1.21.2 triangles:
Figure 1.21.2. Calculation of magnetic field energy.
As a result, the formula for the energy Wm of the magnetic field of a coil with inductance L, created by current I, will be written as the formula:
Wм=ΦI2=LI22=Φ22L
Let's use the expression we got for the coil energy to a long solenoid with a magnetic core. Applying the above formulas for the self-induction coefficient Lμ of the solenoid and for the magnetic field B created by the current I, we obtain the entry:
Wм=μ0·μ·n2·I22V=B22μ0·μV
In this formula, V is the volume of the solenoid. The resulting expression demonstrates to us that magnetic energy is not localized in the turns of the coil through which the current passes, but is distributed throughout the entire volume in which the magnetic field arose.
Definition 4
Volumetric magnetic energy density is a physical quantity that is equal to the magnetic field energy per unit volume: Wм=B22μ·μ.
At one time, Maxwell demonstrated that the indicated formula (in our case, derived for a long solenoid) is correct for any magnetic fields.
It's interesting that...
... the German canon von Kleist, who independently of the Dutch professor Muschenbroek conducted an experiment with a Leyden jar and tested its discharge, apparently tried to use it to obtain electrified water, which was considered beneficial to health.
...in 1827, the French scientist Savard discovered that after discharging a Leyden jar through a wire wound on an iron knitting needle, the latter often turned out to be magnetized. What was surprising was that sometimes the north and sometimes the south pole appeared at the same end of the spoke, although the jar was always charged in the same way. The explanation came later - along with an understanding of the oscillatory nature of the discharge.
...Hertz not only did not think about radio communication, but even denied its possibility.
...Rutherford tried to solve the problem of transmitting signals over distances in his own way, different from Popov and Marconi. However, having learned about Marconi's results in 1897, Rutherford stopped further experiments in this area and switched to research on radioactivity.
...Kapitsa proposed a new method for producing pulsed ultra-strong magnetic fields while working at the Cavendish Laboratory. This is how the famous American mathematician Norbert Wiener described the operation of his installations: “... powerful generators... were short-circuited, creating enormous currents that passed through massive wires; the wires hissed and crackled like angry snakes, and a magnetic field of colossal strength arose in the surrounding space.”
About inductance in simple words
Inductance is a physical quantity that was introduced to evaluate the ability of an electrical conductor to resist current. Those. inductance, or as it is also called, the self-inductance coefficient, shows the dependence of Ɛ on the properties of the conductor and on the magnetic permeability of the environment in which it is located. The unit of measurement is henry (H).
If we consider the value using an inductor as an example, we can understand that its performance will vary depending on the number of turns of the coil, as well as its size and shape. The greater the number of turns, the greater the inductance. This value will also be increased if a core is placed inside the coil, since the relative magnetic permeability of the medium in which the conductor is located will change. This relationship can be seen in the diagram.
If you look at the formula for the dependence of EMF on inductance, you can understand that the greater the value, the more noticeable the electromotive force will be, which indicates their direct proportionality. Following from this, we can conclude that inductance acts as a kind of “storage” of energy, which opens at the moment the current changes.
Ɛ=- L(dI/dt), where:
- Ɛ – self-induced emf;
- L-inductance;
- I – current strength;
- t – time.
In this case, L is equal to the magnetic field (Ф) divided by the current strength (I).
How do they conduct alternating current?
To see this with your own eyes, it is enough to assemble a simple diagram.
First you need to turn on the lamp through capacitors C1 and C2 connected in parallel. The lamp will glow, but not very brightly. If we now add another capacitor C3, the glow of the lamp will noticeably increase, which indicates that the capacitors resist the passage of alternating current. Moreover, a parallel connection, i.e. Increasing the capacitance reduces this resistance. Hence the conclusion: the larger the capacitance, the lower the resistance of the capacitor to the passage of alternating current. This resistance is called capacitive and is denoted in formulas as Xc. Xc also depends on the frequency of the current; the higher it is, the less Xc. This will be discussed a little later.
Another experiment can be done using an electricity meter, having first disconnected all consumers. To do this, you need to connect three 1 µF capacitors in parallel and simply plug them into a power outlet. Of course, you need to be extremely careful, or even solder a standard plug to the capacitors. The operating voltage of the capacitors must be at least 400V.
After this connection, it is enough to simply observe the meter to make sure that it is in place, although according to calculations, such a capacitor is equivalent in resistance to an incandescent lamp with a power of about 50 W.