Момент асинхронного электродвигателя
Эквивалентная схема асинхронного электродвигателя, рассмотренная в предыдущей статье, дает возможность получить выражение электромагнитного момента, который развивает асинхронный электродвигатель. Мощность, которая потребляется электрической машиной из сети, будет расходоваться не только на полезную работу, но и потери в контуре намагничивания и в обмотках.
Поэтому выражение мощности будет иметь вид:
На основании формулы (1) можно получить такое уравнение:
В свою очередь мощность электромагнитную можно выразить и таким способом:
Из выше перечисленных уравнений можем получить значение электромагнитного момента:
Помножив знаменатель и числитель этого выражения на S2 и в целях упрощения вида уравнения примем значение Хк = Х1 + Х2/. Хк – сопротивление индуктивное асинхронного электродвигателя при коротком замыкании:
Для упрощения записи, как в равенстве (5), индекс «эм» будет пропускаться.
Момент электромагнитный асинхронной машины представляет собой довольно сложную функцию скольжения S. Для того, чтоб найти максимум момента асинхронной машины приравняем производную S нулю:
Производная станет равна нулю только в том случае, если стоящий в скобках числителя множитель равен будет нулю:
Или же:
Откуда можно выразить скольжение:
Sк называют критическим, так как при переходе S = Sк момент двигателя уменьшится. Это происходит из-за того, что при увеличении роторного тока (S > Sк) его активная часть не вырастет, а наоборот, уменьшится, что в свою очередь приведет к снижению момента.
Если Sк положительно – это режим работы двигательный, а если отрицательный – генераторный.
В асинхронных машин большой мощности r1 значительно меньше, чем Хк, и, как правило, лежит в пределах r1 = 0,1 – 0,12Хк. Поэтому величина r12 существенно мала, по сравнению Хк, и ею можно пренебречь без ущерба для точности:
Подставив положительные значения Sк (6) в выражение (5), найдем значение критического момента для двигательного режима:
Раскрыв скобки в знаменателе (8) и сократив дробь величине Мкд получим:
Для машин большой мощности для которых величиной r1 можно пренебречь выражение (9) примет вид:
Аналогичным образом получается значение критического момента для генераторного режима:
Отношение моментов генераторного и двигательного режимов работы АД:
Поделив числитель и знаменатель на и обозначив соотношение выражение (12) примет вид:
Также ε можно еще выразить как:
Так как асинхронные электродвигатели обычно имеют r1 ≈ r2/, то приближенно можем принять:
Из выражений (12) и (13) можно увидеть, что в генераторном режиме значение критического момента будет больше, чем в двигательном. Это объясняется влиянием падения напряжения в активном сопротивлении статорной обмотки.
Отношение момента электромагнитного, к его критическому значению в двигательном режиме Мдк = Мк, будет иметь вид:
Откуда выражаем:
Данное выражение представляет собой уточненное уравнение механической характеристики асинхронного электродвигателя.
Если принять, как это делалось выше, r1 = 0, то тогда ε = 0 и взамен (15) получим упрощенное уравнение для механической характеристики:
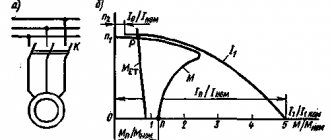
М, выраженный формулами (5), (15) и (16), является функцией скольжения S. Задаваясь различными значениями скольжения S можно построить механическую характеристику асинхронной машины.
Ниже показана механическая характеристика построенная по формуле (15):
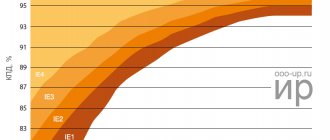
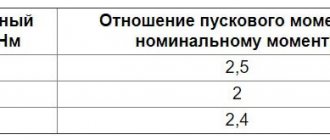
Для машин асинхронных трехфазных с короткозамкнутым ротором общего применение мощностью 0,6 – 100 кВт соотношение должны лежать в пределах 1,7 – 2,2; причем большее значение соответствует большей скорости вращения ротора 3000 об/мин, а меньшее — 750 об/мин. Для машин мощность свыше 100 кВт должны иметь λм = 1,7 – 1,8. Для крановых и металлургических:
Уравнения (15) и (16) имеют значительное преимущество перед уравнением (5) в том, что нет необходимости знать параметры обмоток асинхронной машины и можно вести расчет по каталожным данным электродвигателя.
Но в каталожных данных значение критического скольжения не приводится и их приходится определять из соотношений (15) и (16), используя значения перегрузочных способностей машин λм.
Записав уравнение механической характеристики для Мном получим:
Использовав приближенное равенство ε ≈ Sк, получим:
Данное равенство можно представить в виде квадратного уравнения относительно Sк:
Решив его:
В электрических двигателях большой мощности ε ≈ 0 и уравнение для Sк будет иметь вид более простой:
В выражениях (17) и (18) перед корнем следует брать знак плюс, так как отрицательный знак соответствует нахождению точки Sном, Мном на механической характеристике в зоне где S>Sк. Практического применения данный случай не имеет, поэтому второе решение отбрасывается.
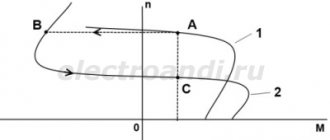
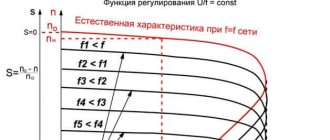
Приведенные выше механические характеристики (5), (15), (16) справедливы только при оговоренных выше ограничениях. Асинхронные электродвигатели имеющие фазный ротор имеют характеристики достаточно точно описываемые данными уравнениями. В машинах с короткозамкнутым ротором имеется процесс вытеснения тока в стержнях ротора. Следствием чего становится непостоянство их параметров и механические характеристики могут значительно отличатся от построенных по формулам (5), (15), (16). Однако от этого данные формулы (особенно (15), (16)) не теряют своего значения, так как благодаря своей простоте они позволяют производить многие расчеты и делать общие заключения о работе асинхронных машин. В случаях когда необходима большая точность применяют экспериментально снятые или специально рассчитанные механические характеристики.
В качестве примера ниже показаны механические характеристики некоторых типов электродвигателей с КЗ ротором:
Похожие материалы:
- Как контроллер микрошагов обеспечивает более плавное…
Работа и мощность
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
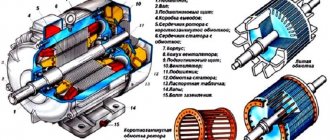
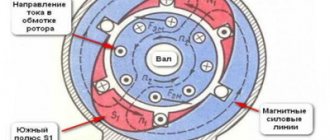
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Постоянный вращающий момент
Переменный вращающий момент и мощность
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Источник
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.