How to convert different units of illumination: lux to lumens calculator

Both the quality of the work performed and the health of the worker who performs it depend on the amount of light in the workplace. Not only this requires a sufficient amount of illumination in lux per unit area. Human habitation on the planet and the normal existence of flora and fauna require a certain standard of illumination. Light sources are natural and artificial emitters.

Illumination per unit area

Typical illumination, examples

The interpretation of the illumination unit 1 lux looks like this: 1 lux (the designation of this value in the SI system) corresponds to the order of illumination of 1 m2 of surface by an incident light flux of 1 lumen (Lm).

When it comes to the brightness of light, there are two positions to consider:

the strength of light emitted by any source;
the amount of light falling on the surface.

The second position is the illumination in question.

Examples of typical illumination values, in accordance with external perception

Illumination value, lux	External perception
0,0001	moonless starry sky
0,01	quarter moon
0,27	full moon in a clear sky
1	the ability to distinguish the outlines of objects, free orientation in space, a short time for vision adaptation when moving from a brightly lit space
5	easy visual perception of the watch dial, the ability to read newspaper headlines
10	illumination of the space next to the candle
15-20	light from a cigarette at a distance of 300 mm
20-35	light in the cinema during intermission
50	you can read the text in the newspaper, lighting the living room
100	allows for long periods of newspaper reading, but is tiring for the eyes
300	comfortable conditions for reading printed materials
400-500	typical lighting for libraries and offices
1000	clear day an hour before sunset
2000	clear morning an hour after sunrise
25000	summer cloudy day at 10 am
65000	clear summer day at 10 o'clock in the morning
100000	midday on a clear summer day

Attention! The determination of the illumination of objects is not limited to visual perception. For this purpose, a device called a “lux meter” is used. This is a simple device, which is based on a photocell that converts light energy into electrical energy and displays the readings on the display. It allows you to measure illumination.

Luxmeter CEM DT 1308

The relationship between the exposure number and the brightness and illumination of the subject

Determining exposure by the brightness of light reflected from the subject

When using exposure meters or lux meters that measure light reflected from the subject, shutter speed and aperture are related to the brightness of the subject as follows:

2 /
t
=
LS
/
K
(2)

N
- aperture number;
t
— shutter speed in seconds;
L
is the average brightness of the scene in candelas per square meter (cd/m²);
S
- arithmetic value of photosensitivity (100, 200, 400, etc.);
K
is the exposure meter or lux meter calibration factor for reflected light; Canon and Nikon use K=12.5.

From equations (1) and (2) we obtain the exposure number

EV = log 2 ( LS

/
K
)

2 EV = LS

/
K
At K

= 12.5 and ISO 100, we have the following equation for brightness:

2 EV = 100 L

/12.5 = 8
L
L

= 2 EV /8 = 2 EV /2 3 = 2 EV–3 .

Length and distance Mass Measures of volume of bulk solids and foodstuffs Area Volume and units of measurement in culinary recipes Temperature Pressure, mechanical stress, Young's modulus Energy and work Power Force Time Linear velocity Plane angle Thermal efficiency and fuel efficiency Numbers Units for measuring the amount of information Exchange rates Dimensions women's clothing and footwear Sizes of men's clothing and footwear Angular velocity and rotation frequency Acceleration Angular acceleration Density Specific volume Moment of inertia Moment of force Torque Specific heat of combustion (by mass) Energy density and specific heat of combustion of fuel (by volume) Temperature difference Coefficient of thermal expansion Thermal resistance Specific thermal conductivity Specific heat capacity Energy exposure, thermal radiation power Heat flux density Heat transfer coefficient Volume flow Mass flow Molar flow Mass flow density Molar concentration Mass concentration in solution Dynamic (absolute) viscosity Kinematic viscosity Surface tension Vapor permeability Vapor permeability, vapor transfer rate Sound level Microphone sensitivity Sound Pressure Level (SPL) Brightness Luminous Intensity Illumination Computer Graphics Resolution Frequency and Wavelength Diopter Power and Focal Length Diopter Power and Lens Magnification (×) Electrical Charge Linear Charge Density Surface Charge Density Volume Charge Density Electric Current Linear Density current Surface current density Electric field strength Electrostatic potential and voltage Electrical resistance Electrical resistivity Electrical conductivity Electrical conductivity Electrical capacitance Inductance American wire gauge Levels in dBm (dBm or dBmW), dBV (dBV), watts and other units Magnetomotive force Magnetic strength fields Magnetic flux Magnetic induction Absorbed dose rate of ionizing radiation Radioactivity. Radioactive decay Radiation. Exposure dose Radiation. Absorbed dose Decimal prefixes Data transmission Typography and image processing Units of timber volume Calculation of molar mass Periodic table of chemical elements D. I. Mendeleev

1 candela [cd] = 1 lumen/steradian [lm/sr]

Initial value

Converted value

candela candle (German) candle (British) decimal candle pentane candle pentane candle (10 light output) Hefner candle Carcel unit candle decimal (French) lumen/steradian candle (international)

Multiples and submultiples

Zener diode TL431

The unit of illumination - lux, like all metric quantities related to each other, has multiple and submultiple units of measurement or designations.

Information. Multiple units are those that are an integer number of times higher than the unit of the original physical quantity, and submultiples are those that are an integer number of times lower than this value.

Multiples and submultiples of lux units (lx)

The illumination of the earth's surface from Sirius is 1*10-5 lux, from the Sun at winter noon - 1*104 lux.

The power of light in museums

Museum staff measure the light intensity in museum spaces to determine the optimal conditions for visitors to view the works on display, while at the same time providing gentle light that causes as little damage as possible to museum exhibits. Museum exhibits containing cellulose and dyes, especially those made from natural materials, deteriorate from prolonged exposure to light. Cellulose provides strength to fabric, paper and wood products; Often in museums there are many exhibits made from these materials, so the light in the exhibition halls poses a great danger. The stronger the light intensity, the more museum exhibits deteriorate. In addition to destruction, light also discolors or yellows cellulose-containing materials such as paper and fabrics. Sometimes the paper or canvas on which the paintings are painted deteriorates and breaks down faster than the paint. This is especially problematic since the paint on a painting is easier to restore than the base.

The damage caused to museum exhibits depends on the wavelength of light. For example, light in the orange spectrum is the least harmful, and blue light is the most dangerous. That is, light with longer wavelengths is safer than light with shorter wavelengths. Many museums use this information and control not only the total amount of light, but also limit blue light using light orange filters. At the same time, they try to choose filters that are so light that, although they filter out blue light, they allow visitors to fully enjoy the works exhibited in the exhibition hall.

It is important not to forget that exhibits deteriorate not only from light. Therefore, it is difficult to predict, based only on the intensity of light, how quickly the materials from which they are made will degrade. Long-term storage in museum spaces requires not only low lighting, but also low humidity and low oxygen levels, at least within display cases.

In museums where flash photography is prohibited, they often refer specifically to the harm of light to museum exhibits, especially ultraviolet light. This is practically unfounded. Just as limiting the entire spectrum of visible light is much less effective than limiting blue light, banning flash has little effect on the extent of light damage to exhibits. During the experiments, the researchers noticed slight damage to the watercolors caused by professional studio flash only after more than a million flashes. A flash every four seconds at a distance of 120 centimeters from the exhibit is almost equivalent to the light that is usually found in exhibition halls, where the amount of light is controlled and blue light is filtered. Those who take photographs in museums rarely use such powerful flashes, since most visitors are not professional photographers and take photos with phones and compact cameras. Flashes in the halls rarely work every four seconds. The damage from the ultraviolet rays emitted by the flash is also in most cases small.

Application in technology

How to charge a lithium ion battery

The widespread use of surveillance cameras to protect objects and organize a surveillance structure requires them to have a certain sensitivity. The sensitivity of these electro-optical devices is measured in lux. This parameter is considered in such devices as a lux meter and a pulse meter.

Example of technical characteristics of the Vt-326 H Wir SpaceTechnology camera

Lux

Lux is the ratio of the number of lumens to the illuminated area.
1 lux is 1 lumen per square meter. Let's say we have a square surface with an area of one meter. The whole of it is evenly illuminated by a light bulb located at some distance vertically from above. For this light bulb, the manufacturer stated an illumination of 100 lux. We take a device called a lux meter and measure at any point in our square, we should get 100 lux. If this is so, the manufacturer did not deceive us. This refers to a light source that shines equally in all directions (Lambertian source). But the LED has the greatest luminous intensity on an axis perpendicular to the plane of the crystal. In other words, by hanging the LED on the ceiling and measuring it with a lux meter, we will see that the further from the axis, the lower the readings of the device. All of you have probably come across incandescent spotlights - these are the so-called “DSLRs”. The back of the bulb of these lamps is covered with a mirror composition, and they only shine downwards. Here's an analogy for you. Features of the practical use of LEDs are in the next article.

(c) Yuri Ruban, February 2009, https://led22.ru. Suggestions and comments are welcome on the forum https://ledway.ru or by email [email protected]

In what units is illumination measured?

If we talk about such a physical quantity as illumination, which is measured in lux, then in the GHS system it is considered in photos.

PTE of power plants and networks

1 phot = 10,000 lux = 1*104 lx, which corresponds to the required level of illumination on the surgical operating table.

For your information. GHS is a classification of absolute physical units (for example, centimeter, gram, second), which was used before the adoption of SI. It was based on three quantities: length, mass, time. The remaining dimensions were reduced to them through mathematical calculations: multiplication, exponentiation and division.

Converting lumens to candelas

Just recently, no one could have imagined that LEDs would so quickly take such a dominant position in the lighting market. LEDs are almost everywhere these days. From indicators in household and computer equipment to road traffic lights and side lights on airplanes and ships.

This happens because LED manufacturers are constantly increasing their brightness characteristics, improving and refining these products to perfectly meet the needs of numerous consumers. In addition, a significant role in the popularity of modern LEDs is played by the constant improvement of manufacturing technologies for their crystals, as well as the use of the latest, high-quality and environmentally friendly materials for the production of such artificial light sources.

All this leads to the fact that today manufacturers of such products must approach the organization of artificial lighting using a variety of LEDs in an extremely comprehensive manner. That is, in addition to the optical properties of LEDs, methods for measuring the main characteristics of any LED: luminous intensity, brightness and luminous flux must also be constantly improved. Let's look at these characteristics in more detail.

Luminous flux is a certain physical quantity that characterizes the amount of light energy emitted in the flux. That is, we are talking about the power of such light radiation that can be perceived directly by the human eye.

Luminance is the flux of light emitted by a unit of surface visible at a unit solid angle in any particular direction. In other words, brightness is a certain photometric quantity that can characterize the emissivity of a body in one direction.

And finally, luminous intensity is the “quantitative” amount of radiation flux per unit solid angle, the limit of its distribution. We can say that luminous flux is the amount of light, calculated in lumens, per 1 steradian.

The most common questions from consumers are “how bright a light output do LEDs produce?”, “what is the intensity of their light in lumens, and what is a lumen in general?”, “how to convert candelas to lumens?”, “why do some measurements not match others measurements? etc. And our converter for converting candelas to lumens and back will help partially answer these questions.

List of basic units of light measurement

With the abundance of various sources of light radiation on the market, confusion arises in terms. The consumer is poorly oriented in the markings applied to lighting devices. The question often arises: 1 lumen is how much lux? There is a significant difference between these concepts.

The main light characteristics include:

lux – the amount of light radiation per unit area;
lumen - the total amount of light emitted by a source around itself;
candela (candle) - the strength of monochromatic radiation from a source in a certain direction.

Important! If we talk about power (W) as a characteristic of a lighting device, then this will not be entirely correct. There is some difference. The power of the luminous flux is measured in lumens. This is the amount of light energy that radiation transfers through any surface per unit time.

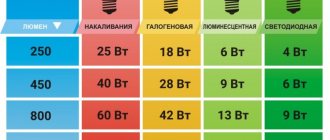
Lumen values for different lighting fixtures

Modern requirements for the packaging of lighting devices require that their technical characteristics be communicated to the consumer in full. Therefore, finding the value in lumens under the abbreviation “lm” or “lm” will be easy. For example:

incandescent lamp 100 W - 1300-1500 lm;
incandescent lamp 60 W "General Electric" - 660 lm;
energy-saving lamp "NetHaus", halogen 13 W - 250 lm;
LED lamp “Gauss Elementary” 12 W “as at 100 W” - 1130 lm;
LED lamp “Gauss Elementary” 6 W “as at 60 W” - 420 lm;
LED lamp Elektrostandard LTB0201D 60 cm 18V - 1200 lm;
LED table lamp Maytoni Nastro, 15 W - 900 lm;
office lamp TL-ECO with LEDs 48.5 W - 4530 lm (total luminous flux after all losses).

Formulas for calculating specific values of candelas, lumens and lux

Currently, there are many programs for gadgets that allow you to convert lumens to lux. The calculator can recalculate and perform the necessary conversion of one value to another online. However, it won’t hurt to learn how to convert lux to lumen and vice versa using formulas.

The first definition you need to know is what a solid angle is. This is an angle that cuts out from a sphere a surface in the form of a circle with area R2 and having a center in a sphere with radius R. It is denoted by the letter Ω, its unit of measurement is 1 steradian (sr).

The angle is found by the formula:

Ω = S/ R2,

Where:

S is the surface area of the spherical segment of the sphere;
R is the radius of the sphere.

After the transformation you get:

Ω = S/ R2 = 4π R2/ R2 = 4π.

Solid angle Ω, graphical representation

The second definition that characterizes a light source is luminous intensity. This physical quantity is designated by the letter I and is measured in candelas (cd, cd).

The luminous intensity formula looks like this:

I = F/ Ω,

Where:

I – luminous intensity, (сd);
F – luminous flux (lm);
Ω – solid angle, (sr).

Determination of luminous intensity

The next quantity that comes into relationship with the previous properties of light is luminous flux. It has the letter F, is measured in lumens (lm, lm ) and is calculated using the formula:

F = I* Ω.

Determination of luminous flux

Lux measures the amount of illumination, which is denoted by the letter E, with the unit of measurement lux (lx, lk). Its formula looks like:

E = F/S,

Where:

E – illumination, lux;
F – flow, lm;
S – area of the illuminated surface, m2.

Using these formulas, you can convert some quantities into others without an electronic “online calculator” program.

Determination of illumination value

Attention! The main physical difference between lumen and lux is that as you move away from the radiation source, the value of illumination (lx) decreases, the value of luminous flux (lm) remains unchanged.

Physical differences between lux and lumen

Lumens, candelas, watts and photons. Different units - different results for measuring the sensitivity of television cameras based on image intensifier tubes and CCDs

“Special equipment”, No. 5, 2002, published with the permission of the editors of the magazine
M.I. Krutik, V.P. Mayorov

The authors of this article work in and by the nature of their activities often encounter some confusion in the minds of our partners and customers regarding the sensitivity of CCD cameras.

This article discusses a method for assessing the sensitivity of television systems (including pulsed ones) using energy units of optical radiation (joule, watt, photon). According to the authors, when registering images, this method is quite universal and applicable across the entire optical spectrum of radiation. In contrast, the calculation method based on lighting units (Candela, lumen, lux) is strictly applicable only within the visible range. Some examples of energy calculations are given that will help the reader see for himself the simplicity of the method and the unambiguity of the results obtained.

Of the many existing television systems, the article considers only CCD cameras, including those with preliminary image intensification stages on electron-optical converters (EOC, English term - image intensifier). The method under consideration may be applicable both for standard television mode (continuous accumulation mode) and for pulsed mode (including single-shot mode).

So that when reading the following material there are no questions about the correctness of the provisions applied, the main definitions from photometry and radiometry are given below.

Introduction

Photometry measures light quantities, and radiometry measures radiation in the entire optical range. Accordingly, light units are often called photometric, and energy units are often called radiometric. The correspondence between photometric and radiometric units is given in Table 1.

Energy					Light
Name	Symbol	Unit			Name	Symbol	Unit
Name	Symbol	Russia	SI system	Quantum analog	Name	Symbol	Russia	SI system
Radiation flux	*F e*	W	W	Nph/s (number of photons per second)	Light flow	*Ф v*	lm	lm
Radiation energy	*Q e*	J	J	Nph (number of photons)	Light energy	Qv	lm*s	lm*s
Energy radiation force (radiation force)	Ie	Tue/Wed	W/sr	Nph/sr s (number of photons in solid angle 1 sr per second)	The power of light	Iv	lm/sr = cd	lm/sr=cd
Surface radiation flux density (luminosity)	*M e*	W/m2	W/m 2	Nph/m2·s (number of photons emitted from 1m2 per second)	Surface luminous flux density (luminosity)	Mv	lm/m 2	lm/m2
Energy illumination (irradiance)	*E e*	W/m2	W/m 2	Nph/m2·s (number of photons per 1m2 per second)	Illumination	Ev	OK	lm/m2= lx
Energy brightness	L e	W/sr*m 2	W/sr*m 2	*Nph/sr m2s** (number of photons in a solid angle in 1sr per 1m2 per second)	Brightness	Lv	lm/sr*m 2 = cd/m 2 = nit	lm/sr*m2 = cd/m2 =nit

Table 1. Basic energy and light quantities, in accordance with the SI system and the International Illuminating Dictionary.
The subscript e for the corresponding values denotes their energetic nature, and the subscript v denotes their photometric nature. Of the entire huge region of the optical radiation region (10 nm - 1 mm), only a narrow spectrum band from 380 to 780 nm (light radiation) can be perceived by the human eye. All metrology in the visible spectrum is based on the eye of a standard photometric observer, whose sensitivity to light radiation is functionally dependent on wavelength. This function V( ) is called “spectral luminous efficiency” V( ). Its graphical form is presented in Figure 1, and its tabular form is presented in Table 2 [1].

Figure 1. Graphical view of spectral luminous efficiency

l, nm	V(l)	l, nm	V(l)	l, nm	V(l)	l, nm	V(l)
380	0,00004	480	0,139	580	0,870	690	0,0082
390	0,00012	490	0,208	590	0,757	700	0,0041
400	0,00040	500	0,323	600	0,631	710	0,0021
410	0,0012	510	0,503	610	0,503	720	0,00105
420	0,0040	520	0,710	620	0,381	730	0,00052
430	0,0116	530	0,862	630	0,265	740	0,00025
440	0,023	540	0,954	640	0,175	750	0,00012
450	0,038	550	0,995	650	0,107	760	0,00006
460	0,060	555	1,0000	660	0,061	770	0,00003
470	0,091	560	0,995	670	0,032
570	0,952	680	0,017

Table 2. Tabular view of spectral luminous efficiency - radiation wavelength in nanometers, V( ) -values of relative spectral efficiency at a given value.
Historically, light measurement metrology developed first. It was the eye, for more than 200 years, that was the standard radiation receiver, on the basis of which all assessments and measurements of light intensity, brightness and illumination were carried out. Subsequently, a device for measuring illumination (lux meter) was created, which has a spectral characteristic that matches the spectral characteristic of the eye of a standard observer.

Television cameras based on CCD matrices and electron-optical image converters (EOCs) have spectral characteristics that differ significantly from the spectral efficiency of the eye. Their range can extend from ultraviolet (120 nm for image intensifier tube) to infrared (1 μm for image intensifier tube and CCD). The use of these devices in conditions where their input receives radiation of a wider spectrum than visible leads to the fact that the readings of a lux meter (measuring radiation only in the visible range) do not carry practically any reliable information. The article will provide a calculation that shows that for a 1/2″ CCD camera matrix, the advertised illumination of 0.0003 lux corresponds to an energy exposure per cell of this matrix of less than 1 photon.

To qualitatively explain such errors, let us consider an example of using a low-level television camera under night conditions with an image amplification cascade on an image intensifier tube with a gallium arsenide photocathode.

Figure 2 shows the relative spectral characteristics:

radiation from the night vault (curve 3) [2];
sensitivity of the gallium arsenide photocathode of the image intensifier tube (curve 2);
the sensitivity of the human eye and the corresponding sensitivity of the device that measures illumination - the Luxmeter (curve 1);
sensitivity of the CCD matrix ICX249 from SONY (curve 4).

Figure 2. Relative spectral characteristics of: various photoelectronic detectors (1,2,4); radiation from the moonless night sky (3)

From the above graphs it is clear that under conditions of a moonless night, the power of infrared radiation of the night arch (>760 nm) significantly exceeds its radiation power in the visible range. In this case, the luxmeter measures only the visible, very small part of the total radiation flux. It is concentrated in the range of 400 - 700 nm. In contrast, the photocathode of the image intensifier tube senses optical radiation in the range of 600 - 900 nm and its photocathode “operates” with a high flux. Similar conclusions are obtained when using a CCD television camera under the same conditions, the silicon crystal of which also has good sensitivity in the infrared range up to 1 μm (curve 4).

From all of the above, we can conclude that for television systems that have spectral characteristics different from the spectral sensitivity of the eye, the use of lighting units (lux, lumen, etc.) is not entirely correct (correct, but not entirely or not at all correct - choice for the reader).

The method for assessing and calculating the sensitivity of television systems in energy units (watt, joule, number of photons) is free from these disadvantages

Basic definitions and constants

First, a few basic definitions. The definition of candela, adopted in 1948 and in effect until 1979, was as follows:

Candela is the intensity of light emitted in a direction perpendicular to 1/600,000 m 2 of the surface of a black body at the solidification temperature of platinum (2042 K) and a pressure of 101,325 N/m2.

Various experiments gave results that showed that at a wavelength = 555 nm, radiation of 1 W corresponds to a luminous flux of 676 - 688 lm. This ratio even then made it possible to convert lumens into watts and vice versa, although opponents still had doubts about the correctness of the method used.

In 1979, the 16th General Conference on Weights and Measures adopted a new definition of the candela [3].

Candela is the luminous intensity in a given direction from a source of monochromatic radiation with a frequency of 540 * 1012 Hz, having a radiation intensity in this direction equal to 1/683 W in a solid angle equal to one steradian.

A radiation frequency of 540*1012 Hz corresponds to a wavelength = 555.016 nm in air under standard conditions, which for almost all purposes can be taken equal to 555 nm without affecting the accuracy of actual measurements.

Based on this fundamental definition, it is possible to unambiguously convert photometric units into radiometric ones and vice versa.

One more (and last) thing we need is a formula for calculating quantum energy. The fact is that in many cases it is more convenient to do energy calculations not in integral quantities (watt, joule and their derivatives), but in quantities of photons (per unit time, per unit area, etc.). In particular, many developers of CCD cameras and qualified users already evaluate their sensitivity by the number of electrons in the cell (in other words, by the number of quanta). Therefore, it is of some interest to calculate the entire photoelectronic complex (input lens + image intensifier tube + projection lens + CCD camera) based on the quantum nature of light. Moreover, such a calculation is very convenient for pulsed irradiation of the recorded image (including single-shot).

The energy of a radiation quantum (photon) is calculated using the well-known formula:

Q = (h * c) / (1)

where: c is the speed of light in vacuum (2.998*108 m/s); h is Planck’s constant (6.6262*10-34 J s); — radiation wavelength (m).

The energy of the radiation quantum at 1 = 555 nm is correspondingly equal to:

Q(1) = 3.58 * 10-19 [J]. (2)

The reciprocal value corresponds to the number of quanta per second in radiation with a power of 1 W at 1 = 555 nm:

Nph [1W] ( 1) = 1 / Q ( 1) = 1 / 3.58 * 10 -19 = 2.79 * 1018 [photo/s] (3)

The subscript ph means that we are talking about photonic quantities. From the definition of candela it follows that at 1 = 555 nm:

Nph [1W] (1) = 683 lm (4)

Therefore, it is possible to obtain the exact value of the number of photons at 1 = 555 nm per second in a luminous flux equal to 1/683 W, which at a given wavelength corresponds to a luminous flux of 1 lm:

Nph [1lm] ( 1) = Nph [1W] ( 1) / 683 = 0.409*10 16 [photo/s] (5)

Using the definition of the unit of illumination, we find that at 1 = 555 nm, the number of photons falling in 1 second onto a surface of 1 m2 at an illumination of 1 lux is:

Nph [1lx] = Nph [1lm] / m2 = 0.409*1016 [phot /(s*m2)] (6)

Now it is possible to show why the use of lighting units (lumen, lux, etc.) in calculating the sensitivity of television systems often gives erroneous results.

For this purpose, a comparative calculation of the average number of electrons in a CCD matrix cell when it is irradiated with the same radiation power at two different wavelengths is provided: 1 = 555 nm and 2 = 630 nm. The readings of the lux meter, in this case, will be a clear demonstration of the assertion being proven. As stated above, its relative spectral characteristic is similar to the relative spectral luminous efficiency of the eye of a standard photometric observer (Fig. 1, Table 2).

To simplify calculations, let us take the radiation flux Fe1 equal to:

Fe1 = 1/ 683 W

At 1 = 555 nm this radiation flux corresponds to the luminous flux

Фv1 = 1 lm

Provided that a given flux falls on an area of 1 m 2 irradiance, the surface of the CCD matrix will be

Ee1 = (1/ 683) W/m2

What corresponds to the illumination

Ev1 = 1 lux

This is the illumination value at 1 = 555 nm and will be shown by the lux meter.

Now the average number of electrons generated in a CCD matrix cell is calculated when it is irradiated with a given flux. As an example, we took a CCD matrix from SONY - ICX249AL (pdf, 221 Kb)

This is a 1/2 inch matrix with the characteristics:

active part size::::.. 6.47 * 4.83 mm
number of active pixels:::.:::::::752 * 582
pixel size:::::::::::::. 8.6 * 8.3 µm
relative spectral characteristic:.(Fig. 2, curve 4)
1 matrix quantum efficiency at (1~ 555 nm) ~ 0.6
2 matrix quantum efficiency at (2 ~ 630 nm) ~ 0.7
accumulation time :::::::::::::::::20 ms

From the above calculations (1) - (6) we found that at 1 = 555 nm irradiance E e1 corresponds to the surface photon density

Nph1( 1) = 0.409*1016 [phot /(s*m2)]

From the calculated pixel area of the matrix

Spix = 8.6 * 8.3 * 10 -12 = 7.14 * 10-11 m2 (7)

and specified accumulation time tn = 20 ms

the number of photons (at 1 = 555 nm) incident on a matrix pixel for a specified time is determined

Nph1-pix( 1) = Nph1 ( 1) * Spix * tн = 5.84 * 103 [photo]

The quantum efficiency of the ICX249 matrix at 1 = 555 nm is approximately 0.6 (Fig. 2, curve 4).

Thus, with irradiation ( 1 = 555 nm) of the surface of the CCD matrix equal to Ee1 = (1/ 683) W/m2, the average number of electrons accumulated in one pixel for t n = 20 ms is

N[el]1-pix = N ph1-pix ( 1) * 0.6 = 3.36 * 10 3 [el] (8)

Here the subscript [el] means that we are talking about the number of electrons.

Now the average number of electrons in a cell is calculated at the same irradiation of 1/683 W/m2, but at 2 = 630 nm.

From (1) we find the quantum energy:

Q (2) = 3.15 * 10-19 [J] (9)

The number of photons in a flow with a power of 1 W in 1 second at 2 = 630 nm is respectively equal to

Nph[1W] ( 1) = 1 / Q ( 2) = 3.17*1018 [photo/s] (10)

and in a flow with a power of 1/683 W, respectively

Nph [1/ 683W] (2) = (3.17*1018) / 683 = 0.46*1016 [phot/s] (11)

Provided that a given flux falls on an area equal to 1 m2, the corresponding photon density (photon irradiance) is equal to

Nph2( 2) = 0.46*1016 [phot /(s*m2)] (13)

Multiplying the obtained value by the area of the matrix cell S pix (7) and the accumulation time t n, we find the number of photons (at = 630 nm) incident on the pixel for the specified time

Nph2-pix( 2) = Nph2 ( 1) * Spix * t n =6.625 * 103 [ph] (14)

The quantum efficiency of the ICX249 matrix at = 630 nm is approximately 0.7 (Fig. 2, curve 4). As a result, we find that the average number of electrons accumulated in one cell over 20 ms is equal to

N[el]2-pix = N ph2-pix ( 2) * 0.7 = 4.64 * 10 3 [el] (15)

It must be recalled that at a wavelength = 555 nm, an energy irradiation of 1/683 W corresponds to an illumination of 1 lx, and at a wavelength = 630 nm, the same irradiance corresponds to an illumination of 0.265 lx. This follows from the spectral luminous efficiency (Fig. 1, Table 2).

Thus, in energy units [W], the sensitivity of the ICX249 matrix at wavelength = 630 nm is approximately 1.4 times greater than at = 555 nm. But in light units [lx] at the same wavelength its sensitivity is already 5.3 times greater (in parrots the boa constrictor turned out to be significantly longer).

Let us summarize the results obtained [(6), (8), (13) and (15)] in Table 3:

Energy exposure	Resp. light illumination [lx]	Quantum energy [J]	Resp. number of photons	Number of photons per CCD crystal in 1 sec S = 5.13* 10-5 m 2	Number of photons per CCD pixel per 1 second s= 7.14* 10 -11m 2	Number of photons per CCD pixel at 20 ms	Number of electrons accumulated in a CCD pixel in 20 ms
1.0 [W/m2 ] at l = 555 nm	683	3,58*10 -19	2.79* 10 18	1,43*10 14	2,0*10 8	4,0* 10 6	saturation
1.0 [W/m2 ] at l = 630 nm	181	3,15*10 -19	3,17*10 18	1,63*10 14	2,26*10 8	4,45* 10 6	saturation
1/683 [W/m2 ] at l = 555 nm	1	3,58*10 -19	4,08*10 15	2,09*10 11	2,93*10 5	5860	3500 (QE=60%)
1/683 [W/m2 ] at l = 630 nm	0,265	3,15*10 -19	4,64*10 15	2,38*10 11	3,31*10 5	6625	4640 (QE=70%)
*1.464 10-5 [W/m2] at l = 555** nm	10 -2	3,58*10 -19	4,08*10 13	2,09*10 9	2930	58	35
*1.464 10-6 [W/m2] at l = 555** nm	10 -3	3,58*10 -9	4,08*10 12	2,09*10 8	293	5 — 6	3 — 4
*1.464 10-7 [W/m2] at l = 555** nm	10 -4	3,58*10 -19	4,08*10 11	2,09*10 7	29	0,5 -0,6	0,3 — 0,4 ?!

Table 3

When illumination on the surface of the matrix is equal to 10 -2 lux ( = 555 nm), a signal charge equal to 35 electrons is formed in each pixel. In this case, what could the sensitivity of 0.0003 lux indicated by the manufacturer mean for the WAT-902H CCD camera, which has an ICX249 matrix installed? With such illumination, during an accumulation time of 20 ms, an average of 1-2 photons arrive per cell, which gives an average of less than 1 electron per pixel.

From Table 3 it can be seen that in order to generate a signal in the CCD matrix equal to the intrinsic noise level of electrons in the cells, the illumination on its surface must be at least 10 -2 lux.

The fact that many CCD cameras are advertised to operate at much lower light levels only speaks to their good infrared sensitivity. But this has nothing to do with luxury suites.

The presented method for assessing the energy sensitivity of photodetectors is given only for monochromatic radiation. Assessing the sensitivity of a CCD or image intensifier when working with non-monochromatic radiation sources requires mandatory knowledge of both the spectral characteristics of photodetectors and the spectral composition of the radiation. The calculation is a kind of convolution of these two functions. In practice, such convolution is most often carried out graphically. Dividing the entire spectral range into intervals within which, with an acceptable error, the value of the radiation power of the source and the quantum efficiency of the photodetector can be considered constant, a calculation is performed for each of the intervals. Then the results obtained are summarized.

Literature

1. M.I. Epstein. Measurements of optical radiation in electronics. "Energy", 1975 2. V.A. Orlov, V.I. Petrov. Surveillance devices at night with limited visibility. M. Military Publishing House, 1989. 3. NIST Special Publication SP330 “The International System of Units (SI).” The US edition of the above BIPM publication.

Addition:
After the publication of this article, it became clear that N.E. came to similar conclusions. Uvarov in his article SECRETS OF HIGH SENSITIVITY TV CAMERAS, published in the magazine “Security Algorithm” No. 6, 2002.

Symbols on light sources

When choosing any light source, be it a light bulb, lamp or spotlight, you must carefully study the markings on the lighting fixture. Even if we remember that the amount of illumination is measured in lux, this data may not be found among the information. Marking applied to the visible part of the bulb or to the lamp body:

manufacturer's trademark;
the amount of voltage used, V;
number of lamps in the lamp and power;
lamp name and type;
protection class;
installation method;
date of manufacture.

In some cases, the permissible distance to the illuminated surface is indicated if the lamp can cause a change in the temperature regime of the illuminated object.

Decoding the lighting fixture markings

Main conclusions

It is not necessary for the average consumer to know the exact definitions of the concepts used in the calculations of lighting systems. If you just need to replace a burnt-out light bulb, just remember that a watt is not a lumen at all. The first determines power, the second determines illumination. When switching to another type of light source, it is quite possible to do without calculations if you find a table on the Internet.

Now, when buying lamps, you need to focus not on watts, but on lumens, and remember that this indicator largely depends on the design of the source. For example, a fluorescent lamp is quite capable of providing 2500-2500 lumens, and the indicator depends on the characteristics of the bulb. Most often, problems are caused by LED sources if low-quality products are purchased.

When choosing, it is also necessary to take into account the decrease in the brightness of the glow during operation. Indicators vary from source to source. An incandescent lamp can lose up to 15% of the flux, a fluorescent lamp can lose up to 30%, and an LED lamp can lose up to 5-10%. When purchasing, be sure to take into account the required stock.

If you are carrying out independent repairs that involve changing the lighting system, it is better to order a lighting calculation. Any mistake may result in additional costs. It is impossible to independently take into account all the nuances without special software. If you choose the right specialist, he will help you choose the type of lamps that will save on electricity. After installation there will be no unpleasant surprise in the form of insufficient light levels.

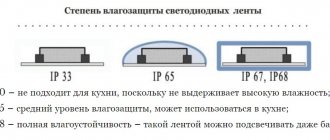
Illumination and LED devices

In the organization of lighting, LED lamps, LED luminaires, LED panels and strips are becoming increasingly popular. An LED lamp is a device that includes:

panel with RGB LEDs;
LED power supply (driver);
heat dissipation panel (radiator);
base and bulb;
lower and upper holders.

The illumination of the object is regulated by the number of LEDs installed in the lamp. The spectrum of white color varies from cool to warm, thanks to RGB LEDs. Three semiconductor chips in one package emit three basic colors: red (R), green (G), blue (B).

Light

Important! LED sources have high light output parameters. F – luminous flux, ranges from 50 to 100 lm per 1 W of power. This is 2-3 times more than halogen lamps, and almost 6 times higher than incandescent lamps.

LED sources practically do not lose power to heat the housing. Long service life (up to 100 thousand hours) with an efficiency factor (efficiency) of more than 85%.

Ordinary LED - what to eat it with

The first semiconductor in history was Ivan Susanin.

No matter how you look at it, you will first have to touch on the laws of ordinary electricity. In illustrative examples, of course. We all know what 220 volts is - this is something that can seriously knock if precautions are not taken. When you buy an electrical appliance, for example, an iron, the passport says what voltage it is designed for. Usually it is 220 volts. But in the same passport the following parameters are also indicated - alternating voltage with a frequency of 50 hertz. Why do manufacturers stubbornly indicate these parameters for you? Pick up any technical data sheet for an electrical device and look - it states that the supply voltage should be ~ 220 volts, 50 Hz. Let's figure out what it is. The "~" sign means the voltage should be variable. In a car on-board network, for example, the voltage is constant. And with a AA battery it is constant. The difference is simple - direct voltage has a plus and a minus, while alternating voltage does not. Why not ? Everything is very simple. In a network with alternating voltage, plus and minus constantly change places. The same contact is sometimes a plus, sometimes a minus. How often ? But for this there is another value - 50 Hz. What is Hz? This is one vibration per second. That is, in our home network, plus changes with minus fifty times per second. And now - what is the practical use of this knowledge, what does this have to do with the LED? Let's figure it out. Let's say you have a 220 volt 100 watt light bulb in your hands. If you plug it into the electrical network, it will light up at its full hundred watts. What if we don’t need these 100 watts? Do you need, say, 50 W? A DIODE will help us with this.

If we break the word “ LED ” into its components, we get “ light ” and “ diode ”. That is, this is an ordinary diode that also glows. A diode is a device that is best compared, for example, to a valve or nipple in a car wheel. You can pump air in there, but the nipple won’t let you back in. A regular diode looks like a black barrel with two terminals - plus and minus. So we can use it for practical experiments, which help many to consolidate the material. Of course, it is dangerous to start experiments immediately with 220 volts, but with due care nothing terrible will happen. However, you conduct all experiments at your own peril and risk. We will need a 220V, 15 W refrigerator light bulb. For it you need to find a suitable cartridge and remove two wires from it. Then we will need any diode that can be obtained, for example, from any faulty TV or tape recorder. The larger it is, the better. There is no need to take very small ones - 220 volts after all. There is usually a triangle symbol next to it. Then we need a power cord with a plug, some wires and a soldering iron. To get started, just connect the light bulb to the network and remember how it glows. Then disconnect and reassemble the circuit according to the diagram on the left. Be sure to carefully insulate all connections with electrical tape. Plug in. As you can see, the light bulb shines much worse. This is not surprising - she now receives only half the voltage she needs - the diode does not allow the second. If your experiment was successful, and the diode is large enough, you can now make any of your light bulbs practically eternal. For example, you have a 50-watt lamp in your hallway and it constantly burns out. Take a 100-watt one, turn it on through a diode - it will shine at about 50 watts, but it won’t burn out. There is, however, one nuance - the diode must be designed for a voltage of 350-400 volts and a current of at least an ampere. It is best to buy one at a radio parts store.

Well, since we have figured out what a diode is, it makes sense to move on to the topic that interests us - LED . The LED, as is now clear, also has a plus and a minus. That is, for its operation you need a constant voltage source - a battery, a battery, a power supply. The power supply must indicate that it produces constant voltage (DC). Usually there is a sticker with this content on the cover of the unit. Input - ~220V 50HZ, output - 12v, 0.5 A DC This means that such a unit can produce a constant voltage of 12 volts and a current of 0.5 amperes. Note that a cell phone charger is also a power supply. It usually has parameters of 5-6 volts, 0.2-0.5 A. It is often very convenient to use it to power LEDs, because the charger stabilizes the current. But more on this later, in the following articles. Two parameters are important to us - the operating voltage of the LED and the current. The operating voltage of an LED is also called “voltage drop”. In essence, this term means that after the LED, the voltage in the circuit will be less by the size of this very drop. That is, if we supply power to an LED , which has a voltage drop of 3 volts, then it will consume these three volts, and the device connected after it in the same circuit will receive 3 volts less. But the most important thing to understand is that LEDs care about current, not voltage. It will take as much voltage as it needs, but as much current as you give. That is, if your power supply can produce 10 amperes, the LED will take current until it burns out. The logic here is simple - the connected LED consumes current and begins to heat up. The more it heats up, the more current can pass through it; it expands when heated. Along with the current, the voltage drop across the diode increases. And so on until it burns out completely - no one has limited the current. And this must be done using a limiting element. Note that if the power source has an output voltage equal to the operating voltage of the LED, there is no need to limit the current. That is, if you have, for example, a white LED and a 3.6-volt battery from a cell phone, you can connect it directly to this battery and the LED will not do anything. He would be happy to grab more current - but there is not enough voltage. So a 3.6 V cell phone battery is an ideal power source for experimenting with white and blue LEDs. Why only with them? More on that in other articles. In general, we need to put a tap in series with the LED and turn it to the value we need. Various devices can act as such a faucet. The simplest of them is a resistor. How to properly limit the LED current is discussed in my article on connecting LEDs in cars. And we will move on. True, if you are not interested in how an LED works, but just want to learn about its practical application, it is better to go to the end of the page and select another part “For Dummies”. But if you are determined to learn about solid-state light sources “from the basics,” let’s continue our acquaintance

Recommended lighting levels for residential premises

During the construction and further operation of premises intended for housing, the lighting of living rooms is calculated. The lack of light, both natural in the daytime and artificial in the evening and night hours, has a detrimental effect on people's health. Therefore, when calculating the number of lighting fixtures and making the necessary measurements of illumination on site, they adhere to the standards that can be found in SNiP.

Residential lighting standards

The unit of illumination is lux, as a parameter of lighting installations is not indicated among the characteristics, but is very important. The height of the source suspension and the angle of the light flux depend on the amount of illumination needed to be obtained on a surface or object.

Where are they used?

The concepts of “Lux” and “Lumen” are applicable to all products that emit light, so they are used to successfully solve the following household problems:

Preventing excessive energy consumption for the operation of lighting devices.
Checking and determining the lighting in a residential area for compliance with the standard. A lux meter is used for measurement.

Luxmeter

Arrangement of lamps to create the same illumination anywhere in the room.
Prevention of eye diseases arising from lack of light.

Important! SanPiN rules dated 2.2.1/2.1.1.1278-03 establish the average illumination of buildings, institutions, and residential premises. Suites help determine whether a room is lit enough for a person to live and work comfortably.

SanPiN

The standards for artificial lighting in residential premises are as follows:

Corridor, bath and toilet – 50 Lx;
Dressing room – 75 Lux;
Children's room – 200 Lux;
Office – 300 Lux;
Kitchen, living room – 150 Lx.

Video

Coffee capsules Nescafe Dolce Gusto Cappuccino, 8 servings (16 capsules)

435 ₽ More details

Coffee capsule Nescafe Dolce Gusto Cafe O Le Coffee with milk, 3 packs of 16 capsules each

1305 ₽ More details

24 inch TVs

How to Convert Luxes to Lumens

However, if you know the required illumination value in lux and the area of the illuminated surface, you can calculate the required luminous flux in lumens. It should be understood that the calculation will be performed with many assumptions, since it is not possible to bring the conditions for its implementation closer to physically ideal ones. When calculating, it should be assumed that:

the light source is located in the center;
the illumination is uniform over the entire area, which is practically impossible;
light falls on the entire surface area at the same angle;
the surface is illuminated from within the mental sphere supposed to surround the source.

Important! The practical formulation of this problem sounds much simpler: there is a standard of illumination in lux for a specific room, for example, for an office - 300 lux. How many lamps do you need to place to comply with it? To do this, first calculate the required value in lumens. The inevitable unevenness in illumination can be corrected with additional lighting.

In order to get the value in lumens, you need to multiply the standard in lux by the value of the area that needs lighting.

Example: Let an office with a standard of 300 lux have a wall length of 10 meters and a ceiling height of 4 meters. It is necessary to calculate the minimum number of lumens required to comply with the standard.

The floor and ceiling area will be: 10 x 10 = 100 m². Area of each wall: 4 x 10 = 40 m². Theoretically, with the assumption of uniform illumination and the location of the source, equidistant from all points of the surface, the problem is solved as follows: 300 lux x (4 x 40 + 100 + 100) m² = 300 x 360 = 108,000 lm. If this astronomical value is “translated” into ordinary 100-watt incandescent lamps, then you will only need... 72 pieces.

The practical approach will be different. There is absolutely no need to illuminate the ceiling - employee workplaces are located below. Moreover, the design of many ceiling lights makes it impossible for light to spread upward. This means you need to remove the ceiling area from the calculations:

300 lux x 260 m² = 78,000 lumens.

Modern LED ceiling lights can produce 5,000 lumens. Accordingly, 16 pieces (78,000/5000) will be required, rounded to the nearest whole number.

This number can be reduced. According to SanPiN 2.2.1/2.1.1.1278-03, illumination is measured above the working surface, as well as at control points 1 m away from walls and light openings. It is enough to place lighting fixtures above employees’ workplaces. Mathematically reducing the geometric characteristics of the floor by 1 m on each side, we get:

300 lx x (160 + 64) m² = 300 x 224 = 67200 lm. What in the ceiling lights will be: 14 pieces, rounded to the nearest whole number.

Notes and links

Derived SI Units, National Institute of Standards and Technology.
"Lux". Illumination/Radiation, quantities and units
. International Electrotechnical Commission. 1987. Retrieved November 30, 2022.
NIST Guide to SI Units. Chapter 9 - Rules and Styles for Writing Unit Names, National Institute of Standards and Technology.
^ a b c d e
Schlieter, Paul (1997–2009). "Radiometry and photometry in astronomy." Starlight illuminance is the same as the minimum illuminance of the human eye, while moonlight is the same as the minimum illuminance of the human eye's color vision (IEE Reviews, 1972, p. 1183).
Kyba, Christopher C.M.; Mohar, Andrey; Posch, Thomas (1 February 2017). “How bright is the moonlight?” Astronomy and Geophysics
.
58
(1): 1.31–1.32. Doi:10.1093/astrogeo/atx025.
"Handbook of Electro-Optics" (pdf). photonis.com
.
item 63. Received April 2, 2012. [ dead link
]
“NOAO Comments and Recommended Indoor Light Levels” (PDF).
^ a b
Grouchy, Alan (June 1998).
"Chapter 7: Appliance Technologies and Emissions Reduction Opportunities." Strategic Study on Home Energy and Greenhouse Gases
(PDF).
Sustainable Solutions Pty
Ltd. Department of Industry and Science of the Commonwealth of Australia. paragraph 61. Archived from the original (PDF) on March 2, 2011. Retrieved June 26, 2008.
Australian Greenhouse Authority (May 2005). "Chapter 5: Estimating Lighting Savings." Energy Work Resource and Training Kit: Lighting
. Archived from the original on April 15, 2007. Retrieved March 17, 2007.
"Low Light Performance Calculator." Archived from the original on June 15, 2013. Retrieved September 27, 2010.
Darlington, Paul (December 5, 2022). "London Underground: Lights Out." Railway engineer
. Retrieved December 20, 2022.
"How to Use a Light Meter (Australian Recommendation)" (PDF). Sustainability Victoria. April 2010. Archived from the original (PDF) on July 7, 2011.
"Illuminations. - 1926.56.” Regulations (standards - 29 CFR)
. U.S. Department of Labor Occupational Safety and Health Administration. Archived from the original on May 8, 2009.
European law UNI EN 12464
^ a b
Schlieter, Section 7.
Schlieter, Section 14.
Jack L. Lindsay, Applied Lighting Engineering
, Fairmont Press, Inc., 1997 ISBN 0881732125 p. 218