The author of the article is a professional tutor, author of textbooks for preparing for the Unified State Exam Igor Vyacheslavovich Yakovlev
Topics of the Unified State Examination codifier: alternating current, forced electromagnetic oscillations.
Alternating current
- these are forced electromagnetic oscillations caused in an electrical circuit by a source of alternating (most often sinusoidal) voltage.
Alternating current is present everywhere. It flows through the wires of our apartments, in industrial electrical networks, and in high-voltage power lines. And if you need direct current to charge your phone or laptop battery, you use a special adapter that rectifies the alternating current from the outlet.
Why is alternating current so widespread? It turns out that it is easy to obtain and ideally suited for transmitting electricity over long distances. We will talk about this in more detail in the leaflet devoted to the production, transmission and consumption of electrical energy.
Now we will look at the simplest AC circuits. We will connect to the AC voltage source one by one: a resistor with a resistance, a capacitor with a capacitance and an inductor. Having studied the behavior of these elements, we in the next sheet “Alternating Current. 2" let's connect them simultaneously and examine the passage of alternating current through an oscillatory circuit with resistance.
The voltage at the source terminals varies according to the law:
(1)
As you can see, voltage can be positive and negative. What is the meaning of the voltage sign?
It is always assumed that the positive direction of the circuit traversal is selected. Voltage is considered positive if the electric field of the charges forming the current is in a positive direction. Otherwise the voltage is considered negative
.
The initial voltage phase does not play any role, since we are considering processes that are established over time. If desired, instead of the sine in expression (1), one could take the cosine - nothing would fundamentally change.
The current voltage value at a time is called the instantaneous voltage value
.
Quasi-stationary condition
In the case of alternating current, one subtle point arises. Let's assume that the circuit consists of several elements connected in series.
If the source voltage changes according to a sinusoidal law, then the current strength does not have time to instantly take on the same value throughout the entire circuit - it takes some time to transfer interactions between charged particles along the circuit.
Meanwhile, as in the case of direct current, we would like to consider the current strength to be the same in all elements of the circuit. Fortunately, in many practically important cases we actually have the right to do this.
Let's take, for example, alternating voltage frequency Hz (this is the industrial standard in Russia and many other countries). Voltage fluctuation period: s.
The interaction between charges is transmitted at the speed of light: m/s. In a time equal to the oscillation period, this interaction will spread over a distance:
m km.
Therefore, in cases where the length of the circuit is several orders of magnitude less than this distance, we can neglect the propagation time of the interaction and assume that the current strength instantly takes on the same value throughout the entire circuit.
Now consider the general case when the voltage oscillates with a cyclic frequency. The period of oscillation is equal, and during this time the interaction between charges is transmitted over a distance. Let be the length of the chain. We can neglect the interaction propagation time if much less:
(2)
Inequality (2) is called the quasi-stationarity condition
.
When this condition is met, we can assume that the current strength in the circuit instantly takes on the same value throughout the entire circuit. Such a current is called quasi-stationary
.
In what follows we assume that the alternating current changes slowly enough that it can be considered quasi-stationary. Therefore, the current strength in all series-connected elements of the circuit will take the same value - its own at each moment of time. It is called the instantaneous current value
.
Electrical resistance
Electrical resistance is a physical quantity that characterizes the resistance of a conductor or electrical circuit to electric current.
Electrical resistance is defined as the proportionality coefficient $R$ between voltage $U$ and direct current $I$ in Ohm's law for a section of a circuit.
The unit of resistance is called ohm (Ohm) in honor of the German scientist G. Ohm, who introduced this concept into physics. One ohm ($1$ Ohm) is the resistance of a conductor in which, at a voltage of $1$ V, the current strength is equal to $1$ A.
Resistivity
The resistance of a homogeneous conductor of constant cross-section depends on the material of the conductor, its length $l$ and cross-section $S$ and can be determined by the formula:
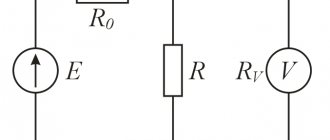
Resistor in AC circuit
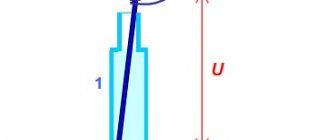
The simplest alternating current circuit can be obtained if a conventional resistor is connected to an alternating voltage source (we assume, of course, that the inductance of this resistor is negligible, so the effect of self-induction can be ignored), also called active resistance
(Fig. 1)
Rice. 1. Resistor in AC circuit
We select the positive direction of bypassing the circuit counterclockwise, as shown in the figure. Recall that current is considered positive if the current flows in a positive direction; otherwise the current is negative.
It turns out that the instantaneous values of current and voltage are related by a formula similar to Ohm’s law for direct current:
Thus, the current strength in the resistor also changes according to the sine law:
The current amplitude is equal to the ratio of the voltage amplitude to the resistance:
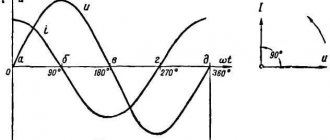
We see that the current through the resistor and the voltage across it change “synchronously”, more precisely, in phase (Fig. 2).
Rice. 2. The current through the resistor is in phase with the voltage
The current phase is equal to the voltage phase, that is, the phase shift between current and voltage is zero.
Features of alternating voltage, current
Generators that produce electricity are designed so that the voltage, the rate of change of charge in our power lines, changes according to a harmonious law:
u = Umsin(ωt+φ0), i = Imsin(ωt+φ0).
Designations:
- u, i – instantaneous values (at an arbitrary moment in time);
- Um, Im – amplitude values (maximum);
- Um – voltage amplitude;
- Im – current amplitude;
- t – time;
- value ω – cyclic frequency.
The value ω is related to the linear frequency ν by the expression:
ω = 2πν:
- π = 3.14 – mathematical constant;
- ν = 50 Hz (for electrical networks in our country).
The product ωt is called the phase:
ωt = φ.
Measured in radians (rad), φ0 is the initial phase, often equal to zero. Using the cos function in formulas does not change the meaning of physical expressions.
If a voltage varying according to a harmonious law is applied to an ordinary resistor (it can be an incandescent lamp, a thermal heater), then particles will begin to move through it, the nature of their movement changing according to the same law.
The change in values will be synchronous, the phases will be the same. This resistance is called active.
Capacitor in AC circuit
Direct current does not flow through the capacitor - for direct current, the capacitor is an open circuit. However, the capacitor is not a hindrance to alternating current! The flow of alternating current through a capacitor is ensured by a periodic change in the charge on its plates.
Let's consider a capacitor connected to a sinusoidal voltage source (Fig. 3). As always, we consider the active resistance of the wires to be zero. We again choose the positive direction of bypassing the circuit counterclockwise.
Rice. 3. Capacitor in AC circuit
As before, we denote by the charge of the plate of the capacitor to which positive current flows - in this case it will be the right plate. Then the sign of the magnitude coincides with the sign of the voltage. In addition, as we remember from the previous sheet, with such a coordination of the sign of the charge and the direction of the current, the equality will be satisfied.
The voltage across the capacitor is equal to the source voltage:
From here
Differentiating this equality with respect to time, we find the current through the capacitor:
(3)
The current and voltage graphs are shown in Fig. 4. We see that the current reaches its maximum each time a quarter of a period earlier than the voltage. This means that the phase of the current is greater than the phase of the voltage (the current is ahead of the voltage in phase by ).
Rice. 4. The current through the capacitor is ahead of the voltage in phase by
You can also find the phase shift between current and voltage using the reduction formula:
Using it, we obtain from (3):
And now we clearly see that the current phase is greater than the voltage phase by .
For the current amplitude we have:
Thus, the amplitude of the current is related to the amplitude of the voltage by a relationship similar to Ohm’s law:
Where
The quantity is called capacitance
capacitor. The greater the capacitance of the capacitor, the smaller the amplitude of the current flowing through it, and vice versa.
Capacitance is inversely proportional to the cyclic frequency of voltage (current) fluctuations and the capacitance of the capacitor. Let's try to understand the physical reason for this dependence.
1. The higher the oscillation frequency (at a fixed capacitance), the less time the charge passes through the circuit; the greater the amplitude of the current and the lower the capacitance. When capacitance tends to zero: . This means that for high frequency current the capacitor is effectively a short circuit.
On the contrary, as the frequency decreases, the capacitive reactance increases, and when we have . This is not surprising: the case corresponds to direct current, and the capacitor for direct current represents infinite resistance (open circuit).
2. The larger the capacitance of the capacitor (at a fixed frequency), the more charge passes through the circuit in the same time (for the same quarter of the period); the greater the amplitude of the current and the lower the capacitance.
We emphasize that, unlike the situation with a resistor, instantaneous
the values of current and voltage at the same instants of time will no longer satisfy a relationship similar to Ohm’s law.
The reason is the phase shift: the voltage changes according to the sine law, and the current strength - according to the cosine law; these functions are not proportional to each other. Ohm's law relates only the amplitude
values of current and voltage.
§ 50. Basic quantities characterizing alternating current
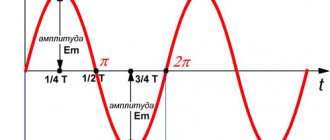
Variable e. d.s., alternating voltage, as well as alternating current are characterized by period, frequency, instantaneous, maximum and effective values. Period.
The time during which the variable e.
d.s. (voltage or current) makes one complete change in magnitude and direction (one cycle), called period
.
The period is designated by the letter T
and is measured in seconds.
If one complete change in the variable e. d.s. takes place in 1/50 sec
, then the period of this e.
d.s. equal to 1/50 sec
.
Frequency.
The number of complete changes in the variable e.
d.s. (voltage or current) performed in one second is called frequency
.
Frequency is symbolized by f
and is measured in hertz (
Hz
).
When measuring high frequencies, the units kilohertz ( kHz
) and megahertz (
MHz
) are used;
1 kHz
= 1000
Hz
, 1
MHz
= 1000
kHz
, 1
MHz
= 1,000,000
Hz
= 106
Hz
. The higher the frequency of the alternating current, the shorter the period. Thus, frequency is the reciprocal of period.
Example.
The duration of one period of alternating current is 1/500
sec
.
Determine the frequency of the current. Solution. One complete change in alternating current occurs in 1/500 sec
. Therefore, 500 such changes will occur in one second. Based on this, the frequency
The longer the period of alternating current, the lower its frequency. Thus, the period is the reciprocal of the frequency, i.e.
Example.
The current frequency is 2000
Hz
(2
kHz
).
Determine the period of this alternating current. Solution. In 1 second,
2000 complete alternating current changes occur. Consequently, one complete change in current - one period occurs in 1/2000 of a second. But based on this period
Angular frequency.
When a coil rotates in a magnetic field, one revolution corresponds to 360°, or 2π radians.
(1 rad
= 57° 17′ 44″; π = 3.14.) If, for example, a coil
makes one revolution T
= 3
seconds
Accordingly, the angular speed of rotation of this turn is expressed in rad/sec
and is determined by the ratio This quantity is called
the angular frequency
and is denoted by the letter ω. Thus,
Since the frequency of alternating current is then, substituting this value f
into the expression for angular frequency, we get:
Angular frequency ω, expressed in rad/sec
, greater than the current frequency
f
, expressed in hertz, 2π times.
If the alternating current frequency f
= 50
Hz
, then the angular frequency
ω = 2πf
= 2 · 3.14 · 50 = 314
rad/sec
In various fields of technology, alternating currents of various frequencies are used. At power plants in the USSR, generators are installed that produce alternating electromotive force, the frequency of which is f
= 50
Hz
.
In radio engineering and electronics, alternating currents with frequencies ranging from tens to many millions of hertz are used. Instantaneous and maximum values.
The magnitude of variable electromotive force, current, voltage and power at any time is called
the instantaneous values
of these quantities and is denoted by lowercase letters (
e, i, u, p
), respectively.
The maximum value
(amplitude) of the variable e.
d.s. (or voltage or current) is called the greatest value that it reaches in one period. The maximum value of the electromotive force is denoted E
m, voltage -
U
m, current -
I
m. In Fig. 51 it is clear that the variable e. d.s. reaches its value twice in one period.
Effective value.
Electric current flowing through wires heats them regardless of its direction.
In this regard, heat is generated not only in direct current circuits, but also in electrical circuits through which alternating current flows. If an alternating electric current flows through a conductor with resistance r ohm
, then a certain amount of heat is released every second. This amount of heat is directly proportional to the maximum value of the alternating current. It is possible to select a direct current that, flowing through the same resistance as the alternating current, would release an equal amount of heat. In this case, we can say that on average the action (efficiency) of alternating current in terms of the amount of heat generated is equal to the action of direct current. The effective (or effective) value of alternating current is such a direct current force that, flowing through equal resistance and in the same time as alternating current, releases the same amount of heat. Electrical measuring instruments (ammeter, voltmeter) connected to the alternating current circuit measure the effective value of current and voltage, respectively. For sinusoidal alternating current, the effective value is 1.41 times less than the maximum, i.e., times.
Similarly, the effective values of alternating electromotive force and voltage are also 1.41 times less than their maximum values.
From the measured effective values of alternating current, voltage or electromotive force, their maximum values can be calculated:
E
m =
E
1.41;
U
m =
U
1.41;
I
m =
I
1.41; (55)
Example.
A voltmeter connected to the circuit terminals shows the effective voltage
U =
127
V. Calculate the maximum value (amplitude) of this alternating voltage. Solution. The maximum voltage value is several times greater than the effective voltage, therefore
U
m =
U
· = 127 · 1.41 = 179.07
V
To characterize each variable electromotive force, alternating voltage or alternating current, it is not enough to know the period, frequency and maximum value.
Phase. Phase shift.
When comparing two or more variable sinusoidal quantities (emf, voltage or current), it is also necessary to take into account that they can change unequally over time and reach their maximum value at different times.
If in an electrical circuit the current changes over time in the same way as the e. d.s., i.e. when the electromotive force is zero and the current in the circuit is zero, and with increasing e. d.s. to a positive maximum value, the current strength in the circuit simultaneously increases and reaches a positive maximum value, and further, when e. d.s. decreases to zero and the current simultaneously becomes zero, etc., then in such a circuit the alternating electromotive force and the alternating current are in phase. In Fig. Figure 52 shows the moments of rotation of two conductors in a magnetic field and graphs of changes in e. d.s. in the wires. Wire 1
and wire
2
are shifted by an angle φ = 90°.
When the magnetic flux crosses, a variable e appears in each of the wires. d.s. When the electromotive force in wire 2
is zero, in wire
1
it will be maximum.
2
in the wire .
d.s. gradually increases and reaches its maximum value at time t
1, and in wire
1
the induced e.
d.s. gradually decreases and at the same moment in time is equal to zero. Thus, induced e.g. in wires. d.s. do not coincide in phase, but are shifted relative to each other in phase by 1/4 of a period or by an angle φ = 90°. In addition, e. d.s. in wire 1
it reaches its maximum earlier than e.
d.s. in wire 2
, and therefore it is believed that the electromotive force
e
1 is ahead in phase e.
d.s. e
2 or e.
d.s. e
2 lags in phase from e.
d.s. e
1. When calculating alternating current circuits, the phase shift between alternating voltage and current is of great practical importance.
Previous page
| table of contents | Next page |
Meaning of Ohm's Law
Ohm's law determines the current strength in an electrical circuit at a given voltage and known resistance. It allows you to calculate the thermal, chemical and magnetic effects of current, as they depend on the strength of the current.
Ohm's Law is extremely useful in engineering (electronic/electrical) because it deals with three basic electrical quantities: current, voltage and resistance. It shows how these three quantities are interdependent at the macroscopic level.
If it were possible to characterize Ohm's law in simple words, then it would clearly look like this:
It follows from Ohm's law that it is dangerous to close a conventional lighting network with a conductor of low resistance. The current will be so strong that it can have serious consequences.
Problem 1.1
Calculate the current passing through a copper wire 100 m long, with a cross-sectional area of 0.5 mm2, if a voltage of 12 V is applied to the ends of the wire.
The task is simple; it consists in finding the resistance of a copper wire and then calculating the current strength using the Ohm's law formula for a section of the circuit. Let's get started.