Magnetic field energy density and magnetic field strength, calculation formulas

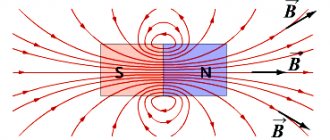
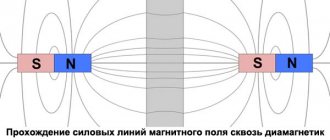
Any electric current is surrounded by a magnetic field. A nontrivial question is the localization of the current's own energy - is it in the conductor where the charges move, or in the magnetic field (the substance that surrounds the current)?

The answer to the question asked is obtained by studying alternating magnetic fields or electromagnetic waves. In an electromagnetic wave, magnetic fields, variable in space and time, can exist in the absence of currents. We know that electromagnetic waves carry energy, therefore we can conclude that energy is localized in a magnetic field.

Volumetric magnetic energy density

The formula for finding the volumetric energy density is as follows:

ω=W/V.

By ω here we mean the actual density being sought, by W the energy of the existing field, and V the volume of space in which the field is active. If we express the value of W in terms of magnetic permeability µ and induction B and substitute it into the formula, it will take the following form:

ω=B2/2* µ0* µ (here µ0 is the magnetic constant).

Conversion using the induction vector is used to eliminate the binding of the active magnetic field to the characteristics of the inductor. The formula for calculating the induction characteristic looks like this:

B= µ0* µ*I*n.

I here is the current force in the coil circuit; n is used to express a value such as the density of the winding. It is equal to the quotient of the number of turns in the solenoid winding and the length of the fragment on which the turns are located. Then the formula for W :

W= B2*V/2* µ0* µ.

By substituting the expression into the basic density formula, you can bring it to the previously designated form.

Flat capacitor.

So, the simplest capacitor consists of two flat conducting plates located parallel to each other and separated by a dielectric layer. Moreover, the distance between the plates should be much smaller than, in fact, the dimensions of the plates:

Such a device is called a flat capacitor , and the plates are called capacitor plates . It is worth clarifying that here we are considering an already charged capacitor (we will study the charging process itself a little later), that is, a certain charge is concentrated on the plates. Moreover, the greatest interest is in the case when the charges of the capacitor plates are identical in magnitude and opposite in sign (as in the figure).

And since the charge is concentrated on the plates, an electric field arises between them. The field of a flat capacitor is mainly concentrated between the plates, however, an electric field also arises in the surrounding space, which is called a leakage field. Very often its influence in tasks is neglected, but it should not be forgotten.

To determine the magnitude of this field, consider another schematic representation of a flat-plate capacitor:

Each of the capacitor plates individually creates an electric field:

• a positively charged plate (+q) creates a field whose strength is E_{+}
• a negatively charged plate (-q) creates a field whose strength is E_{-}

The expression for the field strength of a uniformly charged plate is as follows:

E_{pl} = \frac{\sigma}{2\varepsilon_0\thinspace\varepsilon}

Here \sigma is the surface charge density: \sigma = \frac{q}{S}, and \varepsilon is the dielectric constant of the dielectric located between the capacitor plates. Since the area of ​​the capacitor plates is the same, as is the magnitude of the charge, then the electric field strength modules are equal to each other:

E_+ = E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S}

But the directions of the vectors are different - inside the capacitor the vectors are directed in one direction, and outside - in the opposite direction. Thus, inside the plates the resulting field is defined as follows:

E = E_+ + E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S} + \frac{q}{2\varepsilon_0\thinspace\varepsilon S} = \frac{q}{\varepsilon_0\thinspace \varepsilon S}

Accordingly, outside the capacitor (to the left and right of the plates) the fields of the plates compensate each other and the resulting voltage is 0.

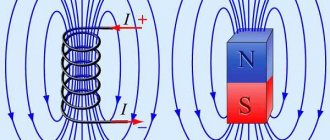
The presence of a magnetic field around a conductor or coil carrying current

When a solenoid (coil) is connected to an electrical circuit, a field is formed around it. The characteristics of the field depend on a number of parameters: on the environmental features of the environment, current strength (measured in amperes) and the material from which the conductor or coil winding is made. Electromagnetic waves can be generated in field space. Since the field energy potential is, first of all, influenced by the strength of the electric current flowing in the system, we can conclude that the work of the current to generate magnetic space will be equivalent to the energy of the latter. If a coil with a magnetic core is connected to the system, then the energy density will be affected by the field energy in the vacuum and in the material from which the core element is made.

Connecting an inductive coil to a current source

What is the source of the magnetic field

To study the dynamics of the phenomenon, you can consider an electrical circuit that includes a choke, a lamp, a closing key and a source of constant electric current. When the switch is closed, the current path will go from the “positive” terminal of the source through the lamp and inductive coil. At first, the incandescent lamp will light up brighter, which is due to the significant value of the inductor resistance. As the resistance drops and the current passing through the winding increases, the intensity of the light bulb will decrease. This is due to the fact that at first the current supplied to the inductor has a value proportional to the high-frequency current.

In order to practically build a circuit suitable for calculation, it is necessary that the energy resource of the power source be spent on generating a magnetic field. Therefore, it is permissible to neglect the parameters of the internal resistance of the inductor and the feed source.

Important! According to Kirchhoff's second law, the sum of the voltages connected to an electrical circuit equals the sum of the voltage drops for all components of the circuit.

Kirchhoff's second law

Notes[ | ]

1. untitled
2. Characteristics of the GESAN DC 1400 generator - power plants and generators from the company svel diesel generator sets
3. Gasoline generator EP-15000TE (Honda) Buy, Europower | Gasoline generators over 6.5kW Sale (unspecified)
   (inaccessible link). Access date: February 12, 2010. Archived August 28, 2009.
4. Gasoline generator for camping and fishing (inverter) EPSi1000 1kW Buy, Europower | Gasoline generators up to 6.5 kW Sale
5. Hymera Generator - Products & Supply > Industrial Products > Hymera | BOConline UK
6. Duracell PROCELL: The Chemistries: Silver Oxide (unspecified)
   (unavailable link). Access date: February 8, 2010. Archived December 20, 2009.
7. Non rechargeable lithium
8. For 425 Ah 6 V battery https://www.cleantorg.ru/catalog/access/access_bat/nba/good140/ Archived copy dated March 28, 2009 on the Wayback Machine
9. For a 190 Ah battery https://www.aktex.ru/
10. https://www.chemi-con.co.jp/e/catalog/pdf/dl-e/dl-dl-e-090901.pdf (inaccessible link)
11. Murata has developed the world's Smallest 1.6×0.8mm Size 10μF Monolithic Ceramic Capacitor Rated at 25V (undefined)
    (inaccessible link).
    Murata Manufacturing Co., Ltd
    (2010). Access date: September 14, 2010. Archived August 23, 2010.
12. For capacitor 947C471K102CDMS with a capacity of 470uF x 1kV weighing 1.3 kg, https://viewer.zmags.com/getMagPdf.php?mid=hwdhd (inaccessible link)

Measuring the energy density of magnetic fields

Magnetic field induction

This value shows the energy contained in a unit volume of the environment subject to the influence of the field. It is denoted by the Greek letter ω. The formula is used for calculation:

ω=W/V, in this case W is the field energy in the volume of space V.

The unit of measurement of field density in the international SI system also looks like a quotient of the units in which these quantities are measured: joules and cubic meters (J/m3). The indicator for batteries (ionic, lead-acid and others) is indicated in the attached documentation.

For a solenoid connected to an electrical circuit, both components of this quotient can be expressed in terms of the following units:

1. The value of the field energy resource will be equal to half the product of the solenoid inductance and the square of the current force in its winding:

W=L*I2/2.

1. The coil itself is considered as the “space”, then V=S*l, where S is the cross-sectional area of ​​the coil element in diameter, and l is its length.

Then the final formula takes the following form:

ω=L*I2/2*S*l.

Footnotes

1. "Two Classes of SI Units and SI Prefixes". NIST Guide to SI
   . 2009-07-02. Retrieved 2012-01-25.
2. "Fossil and Alternative Fuels - Energy Content (2008)." Engineering ToolBox. Retrieved 2018-10-08.
3. Jeong, Gujin; Kim, Hansu; Park, Chung Hwan; Jeong, Jaehwan; Jin, Xing; Song, Juhe; Kim, Bo-ram; Park, Min-Sik; Kim, Ji Man; Kim, Young-Joon (2015). "Nanotechnology Enables Rechargeable Li-SO2 Batteries: Another Approach to Post-Lithium-Ion Battery Systems." Energy and ecology
   .
   8
   (11):3173–3180. Doi:10.1039/C5EE01659B.
4. "Panasonic is developing new high-capacity 18650 lithium-ion cells." Green Car Congress. Np, December 25, 2009. Web.
5. Stura, Enrico; Nicolini, Claudio (2006). "New nanomaterials for lightweight lithium batteries". Analytica Chimica Acta
   .
   568
   (1–2):57–64. doi:10.1016/j.aca.2005.11.025. PMID 17761246.
6. ^ a b c
   Fisher, Julia (2003).
   Ehlert, Glenn (ed.). "Energy Density of Coal". Physics Fact Book
   . Received 2019-07-28.
7. "Thermal Values ​​of Various Fuels - World Nuclear Association." World Nuclear Association. Np, September 2016. Web.
8. "Overview of the U.S. Department of Energy's Hydrogen Storage Development Program." Office of Energy Efficiency and Renewable Energy Sources. Np, May 2000. Web.
9. Wong, Kaufui; Dia, Sarah (2017). "Nanotechnology in batteries." Journal of Energy Resources Technology
   .
   139
   . doi:10.1115/1.4034860.
10. Ionescu-Zanetti, C.; and others. (2005). "Gap Capacitors: Sensitivity to Changes in Sample Dielectric Constant". Journal of Applied Physics
    .
    99
    (2): 024305. Bibcode:2006JAP…. 99b4305I. doi:10.1063/1.2161818. S2CID 120910476.
11. Naoi, K.; and others. (2013). “New generation” nanohybrid supercapacitor.” Chemical Research Reports
    .
    46
    (5):1075–1083. Doi:10.1021/ar200308h. PMID 22433167.
12. Hubler, A.; Osuagwu, O. (2010). "Digital quantum batteries: storing energy and information in nanovacuum tube arrays." Complexity
    .
    15
    (5): no data. doi:10.1002/cplx.20306. S2CID 6994736.
13. Lyon, D.; and others. (2013). "Dependence of the dielectric strength of nano-vacuum gaps on the gap size." IEEE Transactions on Dielectrics and Electrical Insulation
    .
    2
    (4):1467–1471. doi:10.1109/TDEI.2013.6571470. S2CID 709782.
14. Calculated from fractional mass loss times the square of c.
15. Calculated from the square of the fractional mass loss multiplied by c. Ball, Justin (2019). "Maximizing specific energy by deuterium multiplication". Thermonuclear reaction
    .
    59
    (10): 106043. arXiv:1908.00834. Bibcode:2019NucFu..59j6043B. Doi:10.1088/1741-4326/ab394c. S2CID 199405246.
16. Calculated from the square of the fractional mass loss multiplied by c.
17. ^ a b
    "Calculation of the specific energy of nuclear fuel." whatisnuclear.com. Retrieved 2014-04-17.
18. ^ a b c
    College of the Desert, “Module 1, Properties of Hydrogen,” Revision 0, December 2001. Properties of Hydrogen. Retrieved June 8, 2014.
19. Greenwood, Norman N.; Earnshaw, Alan (1997), Chemistry of the Elements (2nd ed) (p. 164)
20. “Boron: a better energy carrier than hydrogen? (February 28, 2009).” Eagle.ca. Retrieved 2010-05-07.
21. ^ a b c d
    Envestra Limited. Natural gas Archived 2008-10-10 on the Wayback Machine. Retrieved October 5, 2008.
22. ^ a b c d e
    IOR Energy. List of common conversion factors (engineering conversion factors). Retrieved October 5, 2008.
23. ^ a b c d e
    Paul A. Kittle, Ph.D. "ALTERNATIVE DAILY COVER MATERIALS AND UNIT D - SELECTION TECHNIQUE" (PDF). Archived from the original (PDF) on 2008-05-27. Retrieved 2012-01-25.
24. "537.PDF" (PDF). June 1993. Retrieved 2012-01-25.
25. Goffman, Evelyn (2003). Ehlert, Glenn (ed.). "Energy value of aviation fuel." Physics Fact Book
    . Received 2019-07-28.
26. "Product Directory" (PDF). Air BP. pp. 11–13. Archived from the original (PDF) on 2011-06-08.
27. Characteristics of stored and released petroleum products
    (PDF), Petroleum Products Division - GN, p. 132, original archived (PDF) January 16, 2022, retrieved January 15, 2017
28. Roman-Leshkov, Yuri; Barrett, Christopher J.; Liu, Zhen Y.; Dumesik, James A. (June 21, 2007). "Production of dimethylfuran for liquid fuels from biomass-derived carbohydrates." Nature
    .
    447
    (7147):982–985. Bibcode:2007Natura.447..982R. Doi:10.1038/nature05923. PMID 17581580. S2CID 4366510.
29. Justin Lemire-Elmore (April 13, 2004). "Energy costs of electric and human-powered bicycles" (PDF). paragraph 5. Received 2009-02-26. a properly trained athlete has an efficiency of 22 to 26%
30. Merue, Lauryn (2020). "Thermal Energy Storage in Silicon". doi:10.1016/j.renene.2019.06.036. Magazine citation required | log = (Help)
31. Bossel, Ulf (July 2003). "The Physics of the Hydrogen Economy" (PDF). European fuel cell news. Archived from the original (PDF) on 2006-03-19. Retrieved 2019-04-06. Higher heating values ​​are 22.7, 29.7 or 31.7 MJ/kg for methanol, ethanol and DME, respectively, while gasoline contains about 45 MJ/kg.
32. "Dimethyl Ether (DME)" (PDF). European Biofuels Technology Platform
    . 2013-11-18. Retrieved 2019-04-06. DME density and lower heating value were obtained from the table on the first page.
33. "Elite_bloc.indd" (PDF). Archived from the original (PDF) on 2011-07-15. Retrieved 2010-05-07.
34. "Biomass Energy Foundation: Fuel Density." woodgas.com. Archived from the original on 2010-01-10. Retrieved 2010-05-07.
35. "Bord na Mona, peat for energy" (PDF). Bnm.ie. Archived from the original (PDF) on 2007-11-19. Retrieved 2012-01-25.
36. Justin Lemire-Elmore (April 13, 2004). "Energy Cost of Electric and Human Powered Bicycles" (PDF). Retrieved 2012-01-25.
37. "energy buffers". Home.hccnet.nl. Retrieved 2010-05-07.
38. Anne Wignall and Terry Wales. Chemistry Textbook 12, p. 138 Archived 2011-09-13 on the Wayback Machine. Pearson Education NZ ISBN 978-0-582-54974-6
39. Mitchell, Robert R.; Betar M. Gallant; Carl W. Thompson; Yang Shao-Horn (2011). "Carbon nanofiber electrodes for high-energy rechargeable Li–O2 batteries". Energy and ecology
    .
    4
    (8):2952–2958. Doi:10.1039/C1EE01496J. S2CID 96799565.
40. David E. Dirks. energy buffers. “household waste 8..11 MJ/kg”
41. Lu, Gui-e; Chang, Wen-ping; Jiang, Jin-Yong; Du Shi-guo (May 2011). "Investigation of the energy density of a powder heat source." 2011 International Conference on Materials for Renewable Energy and the Environment
    . IEEE: 1185–1187. doi:10.1109/ICMREE.2011.5930549. ISBN 978-1-61284-749-8. S2CID 36130191.
42. "Technical Bulletin on Zinc Air Batteries." Duracell. Archived from the original on 2009-01-27. Retrieved 2009-04-21.
43. K. Nowlen, A.T. Mattick, A.P. Bruckner and A. Hertzberg, “High Efficiency Conversion Systems for Liquid Nitrogen Vehicles,” Society of Automotive Engineers, 1988.
44. "Lithium-Ion Battery Review" (PDF). Panasonic. January 2007 Archived (PDF) from the original November 7, 2011
45. "Panasonic NCR18650B" (PDF). Archived from the original (PDF) on 07/22/2015.
46. [44][45]
47. "Duracell Ultra Power AA Test." lygte-info.dk
    . Received 2019-02-16.
48. “Energizer EN91 AA Alkaline Battery Data Sheet” (PDF). Retrieved 2016-01-10.
49. ^ a b
    "Test GP ReCyko + AA 2700mAh (green)".
    lygte-info.dk
    . Received 2019-02-16.
50. ^ a b
    "Maxwell Supercapacitor Comparison" (PDF). Retrieved 2016-01-10.
51. ^ a b
    “Technical description of Nesscap ESHSP series supercapacitors” (PDF). Archived from the original (PDF) on 2016-03-29. Retrieved 2016-01-10.
52. ^ a b
    “Cooper PowerStor XL60 Series Supercapacitor Data Sheet” (PDF). Retrieved 2016-01-10.
53. ^ a b
    “Technical Description of Kemet S301 Series Supercapacitors” (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2016-01-10.
54. ^ a b
    “Technical Description of Nichicon JJD Series Supercapacitor” (PDF). Retrieved 2016-01-10.
55. ^ a b
    "Skelcap high energy ultracapacitor" (PDF).
    Skeletal technologies
    . Archived from the original (PDF) on April 2, 2016. Retrieved October 13, 2015.
56. ^ a b
    "TECHNICAL DESCRIPTION OF ULTRACAPACITOR CELL 3.0V 3400F BCAP3400 P300 K04/05" (PDF). Received 2020-01-12.
57. "Hydropower". www.mpoweruk.com
    . Woodbank Communications Ltd. Retrieved April 13, 2022.
58. “2.1 Electricity, unloading, relations between managers | River Engineering and Restoration at OSU | Oregon State University." river.bee.oregonstate.edu
    . Retrieved April 13, 2022. Let ε = 0.85, which means an efficiency rating of 85%, typical of an older power plant.
59. ^ a b
    “Technical description of Vishay STE series tantalum capacitors” (PDF). Retrieved 2016-01-10.
60. "Technical Data of Nichicon TVX Aluminum Electrolytic Capacitors" (PDF). Retrieved 2016-01-10.
61. “Technical Description of Nichicon LGU Aluminum Electrolytic Capacitors” (PDF). Retrieved 2016-01-10.
62. ^ a b c
    “How much energy can be stored in an elastic band?”
    Wired
    . ISSN 1059-1028. Received 2020-01-21.
63. ^ a b c
    "MatWeb - Internet resource with information about materials."
    www.matweb.com
    . Received 2019-12-15.
64. PubChem. "Acetal". pubchem.ncbi.nlm.nih.gov
    . Retrieved 2019-12-12.
65. ^ a b c d f g h i j k l m p o p q r s t u v
    “Young’s modulus - tensile strength and yield strength for ordinary materials.
    ” www.engineeringtoolbox.com
    . Retrieved 2019-12-12.
66. ^ a b c d f g h i Brush
    Wellman Alloy Products.
    "Elasticity" (PDF). Tech tidbits
    . Retrieved December 15, 2022.
67. “C17200 Alloy Specifications | E. Jordan Brookes Company.” www.ejbmetals.com
    . Received 2019-12-15.
68. "Information and properties of polycarbonate." www.polymerprocessing.com
    . Retrieved 2019-12-12.
69. "ASM Technical Data Sheet." asm.matweb.com
    . Received 2019-12-15.
70. Sutherland, Karen; Martin, Monica (2004). Ehlert, Glenn (ed.). "Density of steel." Physics Fact Book
    . Retrieved 2020-06-18.
71. "Wood species - moisture content and weight." www.engineeringtoolbox.com
    . Retrieved 2019-12-12.
72. ^ a b c
    "Mild/low carbon steel AISI 1018".
    AZoM.com
    . 2012-06-28. Received 2020-01-22.
73. "ASM Technical Data Sheet." asm.matweb.com
    . Retrieved 2019-12-12.
74. ^ a b c
    "American Eastern White Pine."
    www.matweb.com
    . Received 2019-12-15.
75. ^ a b
    "Mass, weight, density or specific gravity of various metals."
    www.simetric.co.uk
    . Retrieved 2019-12-12.
76. “Physical properties of glass | Saint Gobain Building Glass UK.” uk.saint-gobain-building-glass.com
    . Retrieved 2019-12-12.
77. ^ a b
    "Battery Energy Tables". Archived from the original on 2011-12-04.
78. "Battery capacity is 18650."
79. "Supply of uranium." world-nuclear.org. 2014-10-08. Retrieved 2015-06-13.
80. "Cohen Facts". formal.stanford.edu. 2007-01-26. Archived from the original on 2007-04-10. Retrieved 2010-05-07.
81. “U.S. Energy Information Administration (EIA) Annual Energy Review.” Eia.doe.gov. 2009-06-26. Archived from the original on 2010-05-06. Retrieved 2010-05-07.
82. Parravicini, G. (2018). "Thermodynamic potentials in anisotropic and nonlinear dielectrics". Physica
    B.
    541
    : 54–60. Bibcode:2018PhyB..541 … 54P. doi:10.1016/j.physb.2018.04.029.
83. "Terminology". Regenerative laser therapy
    .

Coil inductive reactance formula

Electric field energy

You can calculate the resistance value of the XL throttle using the following formula:

XL=2πfL.

Here the letter L denotes the inductance parameter of the inductor, and f is the current frequency. Based on this expression, at first the current entering the winding will be proportional to the electric current of high purity. At this time, the inductor exhibits behavior similar to a circuit break situation, with a strong increase in inductive reactance. Over time, the latter drops to zero.

The thread built into the lamp has a high resistance value, while the active value of the winding, on the contrary, tends to zero. Because of this, a situation arises where almost all of the circuit current passes through the inductor. When the circuit is opened with a key, the lamp does not go out gradually. On the contrary, it first sharply begins to burn intensely, then slowly fades away. In order for the lamp to burn, an energy resource is required. It comes from the magnetic field generated by the inductive coil. Thus, the choke manifests itself as a source of self-induction.

In the example considered, a coil with windings connected to a circuit acts as a source of a magnetic field. Since in such a situation this field is not uniform, to perform calculations it is necessary to use an indicator characterizing the concentration and distribution of energy in the field. We can conclude that this is precisely the meaning of introducing the field density parameter.