Electrical conductivity of dielectrics. Types of dielectrics, their properties and applications

Terms

Based on the conductivity of electric current, substances are divided into groups:

dielectrics;
semiconductors;
conductors.

Metals conduct current well - their specific electrical conductivity reaches 106-108 (Ohm m)-1.

Dielectric materials are not capable of conducting electric current, so they are used as insulators. They do not have free charge carriers and differ in the dipole structure of their molecules.

Semiconductors are solid materials with intermediate conductivity values.

The crystal grid will help you figure it out

Now the crystal lattice will help us understand electrical dielectrics. So that the terms do not seem incomprehensible to us, let's refresh them in our heads. A crystal lattice is a group of points that are formed in substances (more precisely, in crystals) under the influence of shifts (they, by the way, can occur due to the influence of an electric field. Great, we remembered. Now let's figure it out.

As we remember, in an atom that is currently isolated, the energy of electrons cannot take on any values. In this state, the energy will take on clearly designated values W1, W2, W3, etc. Here, take a look at the graph:

Of course, each of these levels will be slightly shifted after the atoms become part of the solid crystal lattice. As a result, the zone in which all energy will be concentrated will be common to the entire lattice.

So, in a crystal lattice, the energy of electrons lies within well-defined zones and all values that are outside this zone are prohibited. We understood this. Let's move on. According to the Pauli principle, each band can accommodate a limited number of electrons. First, electrons will fill the lower levels, and when these rows are completely filled, they will fill the upper rows.

And now the key idea that you need to understand in order to understand why certain substances conduct electric current. Since electrons gradually fill the rows from bottom to top, then at the topmost row they will either fill this row completely or only partially.

So, when the row is partially filled, electrons will be able to move freely along it, which means they will conduct current. Bingo! But if electrons do fill the upper level, then under the influence of an electric field no shifts will occur and, accordingly, such a substance can be called a dielectric.

A very similar situation occurs with amorphous solids (for example, amber or polyethylene). By definition, in such substances the arrangement of atoms is very random, and zones common to the entire crystal simply cannot exist, which means they are also electrical dielectrics.

Exactly, in addition to electrons, there are also ions, and they can also affect the final situation. Their thermal motion consists of them oscillating somewhere around an equilibrium position. However, the interesting thing is that some of them are still able to break free and overcome what is holding them back.

Such ions can be conventionally called free. They move to places where their potential energy will be very low. If we are talking about electrical dielectrics (and we are still talking about them), then such places in a dense crystal lattice for them are nodes.

So, according to Walter Schottky’s theory, this can only happen when a certain number of lattice sites are already occupied by ions. In physics, such nodes are often called “holes.” Then thermal motion will be reduced to a random jumping of ions from one site to another.

Classification

All dielectric materials are divided into polar and non-polar types. In polar insulators, the centers of positive and negative charges are offset from the center. The molecules of such substances are similar in their electrical parameters to a rigid dipole, which has its own dipole moment. Polar dielectrics include water, ammonia, and hydrogen chloride.

Non-polar dielectrics are distinguished by the coincidence of the centers of positive and negative charges. They are similar in electrical characteristics to an elastic dipole. Examples of such insulators are hydrogen, oxygen, and carbon tetrachloride.

Electrical conductivity

The electrical conductivity of dielectrics is explained by the presence of a small number of free electrons in their molecules. When charges are displaced within a substance over a certain period of time, a gradual establishment of an equilibrium position is observed, which is the reason for the appearance of current. The electrical conductivity of dielectrics exists at the moment the voltage is turned off and on. Technical samples of insulators have a maximum number of free charges, so small through currents appear in them.

The electrical conductivity of dielectrics in the case of a constant voltage value is calculated from the through current. This process involves the release and neutralization of existing charges on the electrodes. In the case of alternating voltage, the value of active conductivity is affected not only by the through current, but also by the active components of polarization currents.

The electrical properties of dielectrics depend on the current density and the resistance of the material.

Where does low electrical conductivity come from?

As we know from the basic physics curriculum, all substances are made of atoms. And these atoms interact very actively with each other. Each of them has its own charge, and thanks to the charges, the atoms interact in one way or another.

However, how is such low electrical conductivity created? It seems that there are atoms, they somehow interact there and current could flow through them, but not everything is so simple. The key to ensuring that the conductivity of a substance is low is a very important fact.

If, when a field is applied, electrons, ions and other particles cannot move freely or do so very poorly, then the electrical conductivity will be low, because everything will stand in its place and free electrons will simply have nowhere to go.

Solid dielectrics

The electrical conductivity of solid dielectrics is divided into volumetric and surface. To compare these parameters for different materials, the values of volumetric resistivity and surface resistivity are used.

Total conductivity is the sum of these two values; its value depends on the humidity of the environment and the ambient temperature. In the case of prolonged operation under voltage, there is a decrease in the through current passing through liquid and solid insulators.

And if the current increases after a certain period of time, we can talk about the fact that irreversible processes will take place inside the substance, leading to destruction (dielectric breakdown).

Place it in a permanent field

Now let's move a little away from what substances can be dielectrics and what cannot be, especially since we have already understood this issue quite well.

Let's now try to answer this interesting question: what will happen if a dielectric is placed in a constant electric field? First, let's give a short answer, and then we will look at this issue in more detail. So, if you place a dielectric in an electric field, then the charges of the dielectric of which it consists will be under the influence of certain forces, which will be:

What will orderly movement provide?

When ordering dielectric charges, there are two possible scenarios:

Features of the gaseous state

Gaseous dielectrics have insignificant electrical conductivity if the field strength is minimal. The occurrence of current in gaseous substances is possible only in cases where they contain free electrons or charged ions.

Bias current

We know that direct current does not flow in a circuit with a capacitor, but alternating current does. The strength of the quasi-stationary current in all elements of the circuit, if they are connected in series, is the same. In a capacitor whose plates are separated by a dielectric, conduction current caused by the movement of electrons cannot flow. This means that if the current is alternating (there is an alternating electric field), some process occurs that closes the conduction current without transferring charge between the plates of the capacitor. This process is called displacement current .

Liquid dielectrics

The electrical conductivity of liquid dielectrics is explained by the structural features of liquid molecules. Non-polar solvents contain dissociated impurities, including moisture. In polar molecules, the conductivity of electric current is also explained by the process of decomposition of the liquid itself into ions.

In this state of aggregation, the current is also caused by the movement of colloidal particles. Due to the impossibility of completely removing impurities from such a dielectric, problems arise in obtaining liquids with insignificant current conductivity.

All types of insulation require a search for options for reducing the conductivity of dielectrics. For example, impurities are removed and the temperature is adjusted. An increase in temperature causes a decrease in viscosity, an increase in ion mobility, and an increase in the degree of thermal dissociation. These factors affect the conductivity of dielectric materials.

How do dielectrics differ from conductors and semiconductors?

The theoretical difference between these three types of materials can be represented, and I will do so, in the figure below:

The drawing is beautiful, familiar from school, but you can’t really get anything practical out of it. However, this graphic masterpiece clearly defines the difference between a conductor, a semiconductor and a dielectric.

And the difference is in the magnitude of the energy barrier between the valence band and the conduction band.

In conductors, the electrons are in the valence band, but not all of them, since the valence band is the outermost boundary. Exactly, it’s like with migrants. The conduction zone is empty, but welcomes guests, since it has plenty of free work places for them in the form of free energy zones. When exposed to an external electric field, the outermost electrons acquire energy and move to free levels of the conduction band. We also call this movement electric current.

In dielectrics and conductors, everything is similar, except that there is a “fence” - a forbidden zone. This band is located between the valence and conduction bands. The larger this zone, the more energy is required for electrons to overcome this distance. Dielectrics have a larger band size than semiconductors. There is even a condition for this: if dE>3Ev (electronvolt) - then it is a dielectric, otherwise dE

In this article, we will further discuss only dielectrics. And since we’ve gone a little deeper into science, let’s talk further about the properties and quantities that characterize these electrical materials in general.

Electrical conductivity of solids

It is explained by the movement of not only the ions of the insulator itself, but also the charged particles of impurities contained inside the solid material. As it passes through the solid insulator, impurities are partially removed, which gradually affects the current conductivity. Taking into account the structural features of the crystal lattice, the movement of charged particles is caused by fluctuations in thermal motion.

At low temperatures, the movement of positive and negative ions of impurities occurs. These types of insulation are typical for substances with a molecular and atomic crystalline structure.

For anisotropic crystals, the conductivity value varies depending on its axes. For example, in quartz in a direction parallel to the main axis, it is 1000 times greater than the perpendicular position.

In solid porous dielectrics, where there is practically no moisture, a slight increase in electrical resistance leads to an increase in their electrical resistance. For substances that contain water-soluble impurities, there is a significant decrease in volumetric resistance due to changes in humidity.

Digital library

General technical disciplines / Materials science (electrical materials science) / 4.1.1. Electrical conductivity of dielectrics

General concepts

Compared to the electrical conductivity of conductors (see Section 2) and semiconductors (see Section 3), the electrical conductivity of dielectrics has a number of characteristic features.

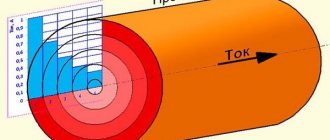
All dielectrics, under the influence of a time-invariant voltage, pass some, albeit very small, current, called leakage current

(I), which consists of two components: volumetric current () and surface current () (Fig. 4.1).

(4.1)

Consequently, the total conductivity of the dielectric () is the sum of the volume () and surface () conductivities:

(4.2)

The reciprocal values of the indicated conductivities are respectively called volume () and surface () resistances.

The next characteristic feature of the electrical conductivity of dielectrics is the gradual decrease in current over time (Fig. 4.2). When a dielectric is connected to a voltage that does not change over time, in the initial period of time a rapidly decreasing displacement current (Icm) flows in the circuit, the density of which is equal to:

This current decreases in a time of 1013...1015 s on the order of the time constant () of the “source-sample” circuit. That is, to a first approximation, we can say that this current is determined by the charging of the geometric capacitance. However, the total current continues to change after this. This decline can continue for several minutes and even hours and is due to the redistribution of space charges

, as well as the establishment of slow (mostly) and fast types of polarization.
This falling part of the current is called absorption current
().

Over time, when the geometric capacitance is charged, i.e. all types of polarization will be established, a redistribution of space charges will occur, and an electric current that does not change over time will remain in the dielectric - through current (), which is due to surface and volumetric electrical conductivities:

. (4.3)

When the resistivity of dielectrics changes, the absorption current must be eliminated by keeping the sample under voltage for some time.

For a comparative assessment of various dielectrics in relation to their volumetric and surface electrical conductivity, volumetric resistivity

(), and
specific surface resistance
().
specific volume conductivity
can be determined :

and according to specific surface resistance - specific surface conductivity

The volume resistivity of a dielectric sample of arbitrary shape can be found from the expression:

(4.4)

where is the volume resistance of a sample of arbitrary shape, Ohm; – geometric parameter, m.

So, for a flat sample, for which (see Section 1), the resistivity is equal to:

, (4.5)

where is the cross-sectional area of the sample (area of the measuring electrode), m2; – sample thickness, m.

Volume conductivity () is measured in siemens per meter ().

Surface resistivity (in ohms) can be found from the expression:

, ………………..(4.6)

where is the surface resistance of the sample, Ohm; – length of electrodes, m; – distance between electrodes, m.

Specific surface conductivity is measured in siemens.

Electrical conductivity of gases

The electrical conductivity of gases is due to the presence of a certain amount of charged particles in them. Under normal conditions, the number of charged particles (gas ions or solid and liquid impurities in suspension) in 1 m3 of atmospheric air does not exceed several tens of millions.

The origin of charge carriers in gases is explained by various factors:

· radioactive radiation of the Earth;

· radiation penetrating from outer space;

· radiation from the Sun;

· sometimes by thermal movement of molecules, etc.

When the energy of a bombarding particle is absorbed, the gas molecule loses an electron and becomes a positive ion. The electron released in this process “sticks” to the neutral molecule, forming a negative ion.

In some cases, the concentration of free charge carriers can reach very high values. This is usually due to photoionization of gas molecules. Such ionization can occur, for example, under the influence of ionizing radiation: X-rays and gamma rays, neutron fluxes, etc. Charged ions, as well as the surrounding gas molecules that do not have an electrical charge, undergo random thermal movements, and due to diffusion, the concentrations are equalized.

tration of ions in gas. When positive and negative ions meet, they recombine. In the stationary case, when the number of ions does not change over time, a dynamic equilibrium is established between the processes of generation and recombination of charged particles.

Let's calculate the specific conductivity of the gas. When an external electric field is applied, positive and negative ions, overcoming the frictional resistance of the gas, will move between the electrodes at speeds respectively:

;

where and are the mobility of positive and negative ions.

The relationship between the number of positive () and negative () ions present in 1 m3 of gas and the number of ions recombining in 1 m3 of gas in 1 s () can be represented as follows:

, (4.7)

where is the recombination coefficient of gas ions, m3/s. For air, for example, m3/s.

In stationary case

So .

If the field strength (E) is very small, so that the flowing current does not change the concentration of ions in the gas, the current density can be determined from the expression:

. (4.8)

Taking into account that , we obtain an expression for the specific conductivity of the gas:

. (4.9)

The specific conductivity of air in weak fields is about 10-15 S/m.

From formula (4.8) it is clear that at low values of the external electric field strength, when , , and can be considered constant, the current density in the gas is directly proportional to the applied field strength, i.e. under these conditions, Ohm's law is observed (Fig. 4.3, section 0A). However, with a further increase in the applied field strength due to an increase in the drift speed of ions, the probability of their recombination decreases, and basically all ions will rush to the electrodes. This is the saturation current (section AB).

For air, with a distance between electrodes of 0.01 m, saturation is achieved at a field strength of 0.5 V/m. The saturation current density in air (under normal conditions) is very small and reaches 10-14 A/m2.

Section 0AB is called the region of non-self-conductivity, since electrical conductivity (concentration of free charge carriers) is determined by the power of external ionizers.

The value of specific air resistance () is about 1018 Ohm∙m. With a further increase in the field strength V/m (Fig. 4.3, section BC), a significant increase in current density occurs due to impact ionization

molecules by electrons in a strong electric field until the breakdown of the gas gap.
The BC section is called the region of independent electrical conductivity
.

Electrical conductivity of liquids

The electrical conductivity of liquids is due to ions formed during the dissociation of molecules of the liquid itself or its impurities. Due to the increase in the energy of the chaotic thermal movement of molecules, the degree of ionization and concentration of ions increases with increasing temperature according to an exponential law:

, (4.10)

where W is the dissociation energy. Hence the specific conductivity is:

, (4.11)

where n is the charge of the ion; and are the mobility of positive and negative ions, respectively; A is a constant.

The logarithm of liquid conductivity decreases linearly with increasing reciprocal absolute temperature 1/T (Fig.

4.4), as in native semiconductors. However, unlike semiconductors, for which , ( is the band gap), the exponent in liquids is determined by their dissociation energy:

The specific resistance of liquids is:

, (4.12)

where B is a constant.

According to a similar law, the viscosity of liquids changes (). The dependence of liquids is explained by both a change and a change in the temperature dissociation of molecules.

The dissociation of molecules occurs more easily in polar liquids than in non-polar ones. Due to the fact that the dissociation energy of polar liquids is much lower than that of non-polar liquids, their specific conductivity is significantly higher. So, for highly polar liquids (distilled water, ethyl alcohol, acetone), for weakly polar (sovol, castor oil), for non-polar (benzene, transformer oil) Ohm∙m. In nonpolar liquids, the molecules of the main substance practically do not dissociate into ions, and their electrical conductivity is due to impurities of especially polar substances.

Molion electrical conductivity is sometimes observed in liquids (and gases) with impurities

, characteristic of
colloidal systems
, which are a close mixture of two phases of substances;
moreover, one phase in the form of small particles (droplets, grains, dust particles, etc.) is evenly suspended in the other. Of the colloidal systems, the most common ones in electrical insulating technology are emulsions
(both phases are liquids) and
suspensions
(dispersed phase is a solid substance, the dispersion medium is a liquid). hundred

the potency of emulsions and suspensions, i.e. their ability to persist for a long time without the dispersed phase settling to the bottom of the vessel (or floating to the surface) due to the difference in the densities of both phases is explained by the presence of electrical charges on the surface of the particles of the dispersed phase (with the same charge, the particles repel each other). Such charged particles of the dispersed phase are called molions

.
When an electric field is applied to a colloidal system, the molions begin to move, which is expressed in the form of electrophoresis
.

Examples of the practical use of electrophoresis are the coating of metal objects with rubber and resins from their suspensions, the dehydration of various materials in an electric field, etc. Unlike electrolysis, the formation of new substances is not observed during electrophoresis, but only the relative concentration of the dispersed phase in different parts of the volume of the substance changes. Molion electrical conductivity is inherent in liquid varnishes and compounds, moistened oils, etc. Its contribution to conductivity, like the contribution of ionic electrical conductivity, depends on the viscosity of the liquid.

Electrical conductivity of solid dielectrics

The electrical conductivity of dielectrics, unlike the electrical conductivity of semiconductors, is most often not electronic, but ionic in nature. This is due to the fact that the band gap in dielectrics is that only a tiny number of electrons can be separated from their atoms due to thermal motion. Ions often turn out to be weakly bound at lattice sites, and the energy W required for their disruption is comparable to kT. For example, in a NaCl crystal eV, and the energy of separation of a sodium ion is eV. Therefore, despite the lower mobility of ions () compared to the mobility of electrons (), ionic conductivity turns out to be greater than electronic conductivity due to a significantly higher concentration of free ions:

. (4.13)

Charge carriers in dielectrics are usually small ions, whose mobility is higher:

· protons in hydrogen-containing compounds (in polymers, crystals like KH2PO4 and others with hydrogen bonds);

· sodium ions (in NaCl and sodium-containing glass), etc.

It should be noted that the number of dissociated (plucked) ions () with a change in temperature changes according to an exponential law:

, (4.14)

where is the total number of ions of the i-th type; – dissociation energy of the i-th type ion; kT – thermal energy.

The specific electrical conductivity of solid dielectrics, like semiconductors, increases with increasing temperature according to an exponential law:

. (4.15)

However, the dependence is often caused not only by an exponential increase in carrier concentration (Fig. 4.5, b)

n~exp(-Wg/kT),

but also by increased mobility:

µ~exp(-Wn/kT),

where Wn is the energy of movement of the ion, which determines its transition from one equilibrium state to another). This is due to the fact that the drift mobility of ions is small and occurs by jumping from trap to trap, separated by a potential barrier Wn (the so-called “hopping” electrical conductivity). The probability of such thermal jumps is directly proportional to exp(-Wn/kT) (Fig. 4.5, a).

Typically, a dielectric contains several types of charge carriers. For example, in addition to ions of the main substance, there may be weakly bound impurity ions. In this case, the specific conductivity is the sum of the intrinsic conductivity with the activation energy (W) and the impurity conductivity with the activation energy (Wnp):

; (4.16)

where is a coefficient combining constants ( – charge of the i-th carrier; – concentration of the i-th carrier; – mobility of the i-th carrier); Wi is the activation energy.

In a wide temperature range, the dependence of the logarithm of specific conductivity (γ) on the reciprocal value of absolute temperature (T) should consist of two straight sections with different values of the angle of inclination to the abscissa axis (Fig. 4.6). At a temperature above the break point A, electrical conductivity is determined mainly by its own defects - this is the high-temperature

, or
intrinsic electrical conductivity
.
Below the kink, in the region of low-temperature
or
impurity electrical conductivity
, the dependence is flatter.

In contrast to the difficult to reproduce low-temperature region of electrical conductivity, which is determined mainly by the nature and concentration of impurities, the value of intrinsic conductivity does not depend on specific conductivity and does not depend on impurities, is well reproducible and is a physical parameter of a given compound.

The temperature at which the inflection point is observed strongly depends on the degree of purity and perfection of the material. As the content of impurities and defects increases, the impurity conductivity increases and turns out to be significant at higher temperatures (Fig. 4.6). From the slopes of the plots of the dependence lines, one can determine the activation energy of charge carriers and their nature.

Ionic electrical conductivity is accompanied by the transfer of matter: positive ions move towards the cathode, and negative ions towards the anode. Electrolysis is especially pronounced at elevated temperatures, when ρ is small, and when high constant voltages are applied. Based on the substance released on the electrodes, the nature of the charge carriers can be determined. In dielectrics with purely ionic conductivity, Faraday's law is strictly observed - the law of proportionality between the amount of electricity passed and the amount of substances released.

Some dielectrics (for example, other titanium-containing ceramic materials) exhibit electronic or hole electrical conductivity. However, the carriers are often electrons not of the main substance, but of impurities and defects. In titanium-containing ceramics, during high-temperature synthesis, oxygen vacancies appear in significant quantities, giving up weakly bound electrons or holes. The observed electrical conductivity depends on them.

Solid porous dielectrics, in the presence of moisture in them, even in insignificant quantities, sharply increase their electrical conductivity (Figure 4.7). In the AB section of the curve, the resistance value decreases as a result of a change in the degree of dissociation of water molecules and dielectric molecules in an aqueous solution into ions. The BC section is caused by drying processes, and in the SD section, the dissociation of dielectric molecules into ions occurs.

We considered the electrical conductivity of solid dielectrics at relatively low electric field strengths. At sufficiently high electric field strengths, an electronic component of electrical conductivity appears in dielectrics, which rapidly increases with increasing electric field strength, and therefore a violation of Ohm’s law is observed. At electric field strengths V/m, i.e. close to breakdown field strengths, the dependence of electrical conductivity on the field strength obeys Poole’s law:

, (4.17)

For a number of dielectrics, Frenkel's law turns out to be more accurate:

, (4.18)

where is electrical conductivity in weak electric fields; – nonlinearity coefficients characterizing the properties of the dielectric; E – electric field strength.

Polarization of dielectrics

This phenomenon is associated with a change in the position of the insulator particles in space, which leads to the acquisition of a certain electric (induced) moment by each macroscopic volume of the dielectric.

There is polarization that occurs under the influence of an external field. A spontaneous variant of polarization is also distinguished, which appears even in the absence of an external field.

Relative dielectric constant is characterized by:

capacitance of a capacitor with this dielectric;
its magnitude in vacuum.

This process is accompanied by the appearance of bound charges on the surface of the dielectric, which reduce the voltage inside the substance.

In the case of the complete absence of an external field, a separate element of the dielectric volume does not have an electric moment, since the sum of all charges is zero and a coincidence of negative and positive charges in space is observed.

What happens if you influence from the outside?

If you apply an external electric field to an electric dielectric, then the free charges of the dielectric will begin to gradually neutralize it. Moreover, this will happen until the electrons run out or the resulting field becomes zero.

To understand what substances can generally interact with electric fields, we need to understand a term such as electrical conductivity. In simple terms, in order to interact with an electric field, a substance must have a fairly low electrical conductivity.

To be more precise, the resistivity should be comparable to 1010 Q-cm or even greatly exceed this value.