The continuous permissible current of a cable is an important performance characteristic that must be taken into account when calculating the conductor cross-section. If an incorrect value is obtained, then during the use of the electrical network the wire will constantly overheat.
A short-term increase in temperature as a result of a short circuit is possible, but an incorrect cross-section threatens to increase the long-term permissible temperature. This will subsequently lead to damage to the insulation and fire.
When installing electrical wiring, you need to determine the required cable cross-section
Basic Concepts
Any metal product consists of a crystal lattice. Electrons and mobile particles pass through it, which is why electricity is transformed into thermal energy. This property is successfully used by manufacturers of heaters and lighting devices. However, in conventional electrical systems, overheating of the cable is unacceptable, since over time it will lead to insulation failure and fire. Therefore, it is important to select the correct cross-section of conductors so that they can withstand the permissible (potential) current loads of the network.
For this, two terms are taken into account:
- wire section;
- current density.
Dependence of current density on cross-section
Even if the correct cross-section of the wire is selected, it can still overheat. There are several reasons: weak contact at the joints or oxidation associated with unacceptable twisting of aluminum and copper conductors.
Wire size
To select the cross-section of the current-carrying core (conductor, and not the entire cable with sheath and insulation), they are guided by two parameters:
- heating within acceptable limits;
- loss of voltage.
Overheating of the underground cable placed in plastic hose tubes is dangerous. In overhead power lines, attention is paid to voltage loss. For combined segments with two different sections, select the larger one, rounding it up to the standard value. Before calculating the cross-section or searching for suitable tabular values, you should determine what the operating conditions will be.
An incorrect choice of cable cross-section can lead to overheating and fire.
To calculate the potential heating, the long-term permissible temperature must be taken into account. The value directly depends on the possible current strength Ip. After using the formula, you will receive the calculated current Iр, which should differ from Iп and be less than its value (in no case more!). When choosing a section, use the following formula:
- Iр = Pн/Un,
Where:
- Pn — rated power, W;
- Un — rated voltage, V.
This formula can be used to calculate currents in conductors with an already established temperature, provided that the cable is not affected by other cooling or warming factors. The value of the continuous permissible current Ip depends on various parameters: cross-section, material of manufacture, insulating shell and installation method.
To check the voltage drop on an overhead power line, use the following formula:
- Up = (U - Un) *100/ Un,
Where:
- U—voltage from the source;
- Un is the voltage at the place where the voltage receiver is connected.
The maximum permissible voltage deviation is 10%.
Current Density
This physical quantity is a vector quantity. To designate it, use the Latin letter J. The calculation formula is as follows:
- J = I/S,
Where:
- I—current strength, A;
- S—cross-sectional area, sq. mm.
Limit current density for aluminum and copper wires
Current density is the volume of current that passes through a conductor of a given cross-section in a certain period of time. Measured in A/sq. mm.
Simple explanation
Current density J is a vector physical quantity characterizing the electric charge flux density at the point under consideration.
Wikipedia
High electrical current density causes the cable to heat up. Therefore, care must be taken not to exceed the permissible current carrying capacity of the line or conductor. In addition, the effective cross-section of the conductor may decrease when exposed to high-frequency signals (skin effect), which increases the current density. Therefore, when choosing a conductor, it is necessary to take into account not only the actual current, but also the frequency of the signal.
Why do you need to calculate the cable cross-section?
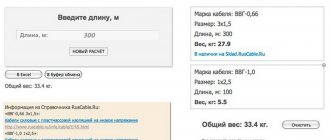
When purchasing a cable, you may see different symbols. For example, a 3x5 wire contains three current-carrying conductors, each of which has a cross-section of 5 square meters. mm. Knowing this, just look at the table of voltage and power.
Only a correctly calculated cross-section guarantees the absence of areas with overheating of the cable. In this case, the wire must withstand temporary loads when the current value is 2-3 times greater than the rated value. You will receive a current reserve, which is important, since at any moment the load on the network may increase due to new household appliances. The absence of heating will prevent spontaneous combustion and fires at objects. This point needs to be thought through in advance, since in most cases a hidden method of installing electrical wiring is used, and the slightest damage can lead to the need to replace the entire line.
Electrical power of household appliances
Choose by power
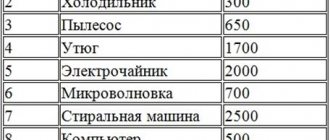
The wire cross-section can be selected depending on the maximum current load on the line. Moreover, each household appliance has a different power. The list below shows the capacities of the most common equipment:
- electric stove - 5 kW;
- refrigeration unit - 0.8 kW;
- dishwasher - 2 kW;
- microwave - 1.5 kW;
- kitchen hood - 0.5 kW;
- kettle - 2 kW.
Obviously, the listed electrical appliances are installed in the kitchen. If you add up all the specified numerical values, you can get the total load on the kitchen electrical network. It will be about 12 kW, but the cross-section should be selected with a margin of up to 30%. Ideally, an electrical cable with a cross-section corresponding to a power of 15-16 kW is laid in the kitchen. To connect the equipment you will need at least two sockets.
The table below shows the selection of copper cable by power:
Determination of copper cable cross-section
The voltage of the electrical network is 220 V. Knowing this parameter and the total load, it is enough to use a simple formula to calculate the current consumption:
- I = P/U = 16,000/220 = 72.7 A.
This is the maximum permissible current for the cable being laid, but in fact the household appliances listed above will consume about 56-57 A. However, it is not necessary to exclude situations when other devices will be connected to the network - a vacuum cleaner, additional lamps, and so on. Many electricians avoid calculations using the coefficient 1.3 (30% margin), and simply add another 5 A to the actual value of the permissible current. If this option was possible before, today it is unlikely. Every year this parameter only increases: more powerful refrigerators, washing machines and vacuum cleaners appear.
The table below shows the selection of aluminum cable by power:
Determination of aluminum cable cross-section
Having completed the calculations of the permissible current, proceed to the selection of material for the current-carrying conductors. Aluminum cable costs less than copper cable, but the cross-sectional area of such conductors should be much higher. The current density for aluminum is 8, copper - 10 A/sq. mm.
Current load on the cable: how to calculate the cross-section
The total amount of current moving through a conductor depends on several characteristics: length, width, resistivity and temperature. An increase in temperature is accompanied by a decrease in current. Any reference information that you find in the PUE tables is usually provided for a room temperature of 18 degrees Celsius.
In addition to the electric current, you need to know the conductor material and voltage. The simplest calculation of cable cross-section based on permissible current is to divide its value by 10. If, when studying the table, you do not find the required value, then look for the nearest, slightly larger value. This option is possible for copper wires, and the permissible current is 40 A or less. In the range of 40-80 A, the permissible current should be divided by 8. For aluminum wires, the value is divided by 6. The reason for this was indicated at the end of the previous section.
Permissible current load on the cable
Application
Current density is especially important in applications where conductor cross-section needs to be optimized for cost, area, and weight reasons. Typically, the conductor cross-section is selected as small as possible to suit the application.
It is important here that the actual current density in the conductor does not exceed the maximum permissible current density. The reason for this is that every electrical conductor has electrical resistance. When electric current flows through this resistance, an electrical voltage drop occurs. As a result, energy is converted and the line is heated. Excessive heat can damage the conductor insulation and cause serious damage.
That is why, for example, permissible current densities for household installations are regulated by relevant standards. In addition, all cables in households are equipped with a fuse that trips before the maximum permissible electric current density is reached.
In the automotive sector, saving weight and space plays an important role. Therefore, cables are also carefully selected here to find a compromise between heating and weight/space.
Calculation of cable cross-section by power and length
The length of the cable determines the voltage loss. One potential unpleasant situation: at the end of the selected wire, the voltage has decreased to a minimum, which is not enough to ensure the functionality of the equipment. In household electrical networks, losses will be small, so they can be neglected. It is enough to use a cable with a margin of 100-150 mm, which is necessary to simplify switching. If the edges of the wire are connected to the electrical panel, then the margin should be higher, since the installation of automatic machines is required.
When placing the cable over longer sections, you need to take into account the voltage drop, which is calculated using the formula given above. Any conductor has a certain electrical resistance, which depends on a number of characteristics:
- Wire length, m. The longer the length, the higher the losses.
- Cross-sectional area, sq. mm. The higher the parameter, the lower the voltage drop.
- Specific resistance of the material (look in reference books).
Maximum cable length for various current loads
To calculate the voltage drop in normal cases, it is enough to multiply the resistance and the permissible current. The actual value may be greater, but not more than 5%. If it does not fit within the specified framework, you will have to use a cable with a larger cross-section.
To calculate the cable cross-section for power and length, proceed as follows:
- Calculate the current using the formula I=P/(U*cosph), where P is power, U is voltage, cosph is coefficient. In household electrical networks, this coefficient is equal to 1, so the formula simplifies to I=P/U. In industry, cosph is the ratio of active and apparent power (active and reactive).
- In the PUE table, find a suitable cable cross-section depending on the current.
- Calculate the conductor resistance using the formula: R=ρ*l/S, where ρ is the resistivity of the material from which the conductors are made, l is the cable length, S is the cross-sectional area. Remember that electric current flows in both directions, so the total resistance is equal to twice the value obtained from the formula above.
- For voltage drop, use the formula ΔU=I*R
- To get the percentage voltage drop, divide ΔU/U.
Thus, if the final value does not exceed 5%, you can leave the cable with the selected cross-section. Otherwise, it will have to be replaced with a conductor with an increased cross-section.
Continuously permissible currents
This value differs depending on the selected cable and the current-carrying cores used. Any wire has a certain long-term temperature Td, which is indicated in its passport. At this temperature, prolonged operation of the conductor cores is permissible, and any damage is excluded.
To calculate the continuous permissible current, use the formula:
- Id = √((Td*S*Kt)/R),
Where:
- Ktp - heat transfer coefficient;
- R - resistance;
- S - core section.
In practice, you can use PUE tables.
Continuously permissible currents for copper wires and cables
Joule-Lenz law. Definition, formula, physical meaning
The Joule-Lenz law is a law of physics that defines a quantitative measure of the thermal effect of electric current. This law was formulated in 1841 by the English scientist D. Joule and completely separately from him in 1842 by the famous Russian physicist E. Lenz. Therefore, it received its double name - the Joule-Lenz law.
Law definition and formula
The verbal formulation has the following form: the power of heat generated in a conductor when an electric current flows through it is proportional to the product of the electric field density value and the intensity value.
Mathematically, the Joule-Lenz law is expressed as follows:
ω = j • E = ϭ E²,
- where ω is the amount of heat released in units. volume;
- E and j are the intensity and density, respectively, of the electric fields;
- σ is the conductivity of the medium.
Physical meaning of the Joule–Lenz law
The law can be explained as follows: current flowing through a conductor represents the movement of an electric charge under the influence of an electric field. Thus, the electric field does some work. This work is spent on heating the conductor.
In other words, energy transforms into another quality – heat.
But excessive heating of current-carrying conductors and electrical equipment should not be allowed, as this can lead to damage.
Severe overheating is dangerous during short circuits of wires, when fairly large currents can flow through the conductors.
In its integral form for thin conductors, the Joule–Lenz law is as follows: the amount of heat that is released per unit time in the section of the circuit under consideration is determined as the product of the square of the current strength and the resistance of the section.
Mathematically, this formulation is expressed as follows:
Q = ∫ k • I² • R • t,
- in this case Q is the amount of heat released;
- I – current value;
- R - active resistance of conductors;
- t – exposure time.
The value of the parameter k is usually called the thermal equivalent of work. The value of this parameter is determined depending on the bit depth of the units in which the values used in the formula are measured.
The Joule-Lenz law is quite general in nature, since it does not depend on the nature of the forces generating the current.
From practice, it can be argued that it is valid both for electrolytes and conductors and semiconductors.
Application area
There are a huge number of areas of application of Joule Lenz’s law in everyday life. For example, a tungsten filament in an incandescent lamp, an arc in electric welding, a heating filament in an electric heater, and many others. etc. This is the most widely accepted physical law in everyday life.
Open and closed wiring
Electrical wiring can be of two types:
- closed;
- open.
In most cases, hidden installation is used for apartments. Using a hammer drill or wall chaser, special recesses are created in the wall or ceiling into which the cable is laid. Additionally, it can be placed in corrugated tubes or sleeves. Having hidden the cable, the recesses should be sealed with plaster. The only acceptable option for modern hidden wiring is copper conductors. In this case, you should consider in advance the potential expansion of the network or the process of partial replacement of its components. Ideally, you should use flat wires.
Laying hidden wiring in grooves
Open electrical wiring involves placing the cable along surfaces. Mainly flexible conductors with a round cross-section are used. They are placed in cable ducts or passed through corrugations. When calculating the load, the cable laying method must be taken into account.
Selection of wire cross-section according to the number of consumers
When calculating cross-sections for an electrical cable in an apartment, it is first recommended to show the wiring schematically. The drawing must indicate all devices that consume electricity. The circuit is divided into different rooms, since each can use a wire of a different cross-section.
Wiring diagram for consumers
The electrical network is divided into several circuits. Each circuit corresponds only to those electrical appliances that are connected to it. To select a cable connecting all circuits, you need to calculate the total total power. This is the main criterion for choosing a section. Each subsequent branching (branch) will lead to a decrease in the total power and, accordingly, a decrease in the required cross-section.
Current loads in DC networks
When calculating the current load in a direct current network, they are guided by a single-core cable. The voltage of this current is 12 V. Calculation of the load of the wire through which a 0.1 kW light bulb is connected (for example, in the headlight of a car) looks like this:
- I = P/U = 100/12 ~ 8.35 A.
After this, it is easy to calculate the resistance:
- R = U/I = 12/8.35 = 1.44 Ohm.
In the table, find the resistivity of copper, from which the cores of modern conductors are made. Also assume that the cable length is 2 m. Use the formula given in the sections above to obtain the cross-sectional area of the suitable wire:
- S = (ρ*L)/R = (1.68*10-8*2)/1.44 = 1.2 sq. mm.
Selecting a cable cross-section for DC networks
When studying the PUE, you can find countless tables that define the current load for AC networks with single- and three-phase circuits. Therefore, it is not necessary to perform such complex calculations.
Bias current density
Displacement current is a rather complex concept in electrodynamics, but it is thanks to it that alternating current passes through the capacitor, and the antenna emits a signal into the air. The displacement current also has its own density, but determining it is not so easy.
Even in a very good capacitor, the electric field “sticks out” slightly to the sides between the plates (Pos. 3 in the figure), so some addition must be given to the surface crossed by the bias current. For a capacitor, its value can still be neglected, but if we are talking about an antenna, then this virtual surface crossed by the bias current means everything.
To find the displacement current density, one has to solve complex electrodynamic equations or perform computer simulations of the process. Fortunately, for many cases of engineering practice it is not necessary to know its value.
Causes of cable heating
Current-carrying conductors can overheat for several reasons, which are directly related to the nature of the electric current. The electric field sets in motion electrons, which move along the selected conductor. In the crystal lattices of which metals are composed, strong molecular bonds operate. Imagine a table tennis ball and a spider web. The second one is more or less durable, the first one is light in weight, so in order for the ball to break the web, more effort will have to be made. The harder you swing, the more tense your muscles will be. The higher the voltage, the higher the energy expended. Accordingly, the muscles will heat up more.
Likewise, electrons are forced to release more heat, spending a lot of energy to overcome these molecular bonds. This process is called the conversion of electrical energy into thermal energy.
This phenomenon can be compared with the release of heat during friction. We can say that electrons are forced to rub against the crystal lattice of the metal and thereby generate heat. This property of a metal cable has its advantages and disadvantages. Heating can be useful in manufacturing facilities and for household appliances. It is the main property that allows electric stoves, heaters, irons and kettles to operate. However, in conventional electrical networks this can lead to overheating and destruction of the insulation, and subsequently even to a fire. Machinery and equipment may deteriorate. A similar thing happens if the specified norm for long-term current loads is exceeded.
We list three main reasons for conductor overheating:
- The most common is the use of a cable with an incorrect cross-section. Any conductor has a unique maximum current carrying capacity. It is measured in Amperes. Before connecting a household appliance, you need to determine its power and, in accordance with it, select the correct cross-section. It is important to take into account a margin of 30-40%.
- The second reason is the lack of high-quality contact at the connection points of the line. We are talking about sections of the route where the cable is connected to a panel, circuit breaker or switch. Poor contact leads to heating. In worst case scenarios - complete burnout. In most cases, it will be enough to inspect the contacts and tighten all connections.
- The old electrical wiring was built on aluminum conductors, so when modernizing such cable lines there is often a need to switch to copper conductors. In this case, it is important to follow the technique for connecting copper and aluminum conductors. Without the use of special terminal blocks, the appearance of oxidation is a matter of time.
Old aluminum wiring in the apartment
Permissible current and wire cross-section
The correct choice of cables and wires during the design and calculations of electrical networks is a guarantee of their reliable and safe operation during further operation. The devices and equipment will receive full power, and the insulation of the conductors will not overheat and be destroyed. Correct calculations of the power cross-section will allow you to avoid emergency situations and the need to restore damaged lines. To do this, you need to know what the essence of such a concept as permissible current for a copper wire is in practice.
In its most simplified form, each cable behaves like a pipeline through which water is transported. In the same way, an electric current moves through cable conductors, the magnitude of which is limited by the dimensions of a specific current-carrying channel, which is actually the cross-section of a given conductor.
The incorrect choice of this parameter often leads to errors and negative consequences. If the current-carrying channel is too narrow, the current density can increase several times. This leads to overheating and subsequent melting of the insulation, resulting in areas with regular current leaks. In the worst case scenario, a fire may occur.
However, too large a current cross-section of wires has one serious drawback in the form of a significant overexpenditure of funds when installing electrical networks. Of course, free transportation of electric current has a positive effect on the functionality and service life of wires, but payments for consumed electricity can increase significantly. Thus, the first option is simply dangerous, and the second is undesirable to use due to its high cost.
Calculation of permissible current for heating cores
If a conductor of a suitable cross-section is selected, this will eliminate voltage drop and overheating of the line. Thus, the cross-section determines how optimal and economical the operating mode of the electrical network will be. It would seem that you can simply take and install a cable with a huge cross-section. But the cost of copper conductors is proportional to their cross-section, and the difference when installing electrical wiring in just one room can amount to several thousand rubles. Therefore, it is important to be able to correctly calculate the cable cross-section: on the one hand, you guarantee the safe operation of the network, on the other hand, you will not spend extra money on purchasing an overly “thick” conductor.
To select the wire cross-section, two important criteria must be taken into account - permissible heating and voltage loss. Having received two values for the cross-sectional area of the conductor using different formulas, choose the larger value, rounding it to the standard. Overhead power lines are especially sensitive to voltage loss. At the same time, for underground lines and cables placed in corrugated pipes, it is important to take into account the permissible heating. Thus, the cross-section should be determined depending on the type of wiring.
Permissible heating temperatures of current-carrying cable cores
Id - permissible load on the cable (heating current). This value corresponds to the current flowing through the conductor over a long period of time. In the process of this, a set, long-term permissible temperature (Td) appears. The calculated current strength (Ip) must correspond to the permissible current (Id), and to determine it you need to use the formula:
- Iр=(1000*Pн*kз)/√(3*Un*hд*cos j),
Where:
- Pn — rated power, kW;
- Kz - load factor (0.85-0.9);
- Un — rated voltage of the equipment;
- hd - equipment efficiency;
- cos j - equipment power factor (0.85-0.92).
It turns out that for any long-term permissible current flowing through the conductor, there corresponds a specific value of the established, long-term permissible heating temperature. It is important to neutralize the influence of other environmental factors. The cable current directly depends on the material from which the insulation is made, the laying method, the cross-section and material of the cores in the conductor.
Even if we take into account the same current values, the thermal output will be different depending on the ambient temperature. The lower the temperature, the more efficient the heat transfer.
Cable correction factors depending on ambient temperature
Temperatures differ depending on the region and time of year, so in the PUE you can find tables for specific values. If the temperature differs significantly from the calculated one, correction factors will have to be used. The base temperature indoors or outdoors is 25 degrees Celsius. If the cable is laid underground, the temperature changes by 15 degrees Celsius. However, it is underground that it remains constant.
SamsPcbGuide, part 3: Printed Track Current Limit
Jokes aside, the topic is serious and flammable. Go. This is the third article in the series, it discusses models for estimating the limiting current of a printed track, which in some situations is the determining parameter when choosing the thickness of the conductive layers of a printed circuit board. The previous article discussed that the choice of the thickness of the copper layers of a printed circuit board is determined, first of all, by the required minimum clearance and minimum conductor width, as well as the maximum current flowing through the conductor. These parameters may contradict each other: the thinner the conductive layer, the smaller the topological pattern can be obtained, but the lower the maximum current the printed track will withstand (other things being equal - conductor width, current frequency, heat sink, etc.). Thermal energy Q released on the ohmic resistance R of the printed track (Joule heat Q=I2Rt, where I is the current strength, t is the time), causes an increase in its temperature relative to the environment, leading to overheating of the conductor itself and associated components or, in extreme cases, case, to its burnout at the limiting current (English fusing current). The relationship between the current through the printed track and the temperature increase depends on many parameters and is difficult to imagine in general terms, but there are formulas that allow you to make preliminary estimates.
Preece, Onderdonk and Brooks
One of the first attempts belongs to W.G. Preece.
He obtained his empirical dependence in a laboratory experiment in which he gradually increased the current through the conductor until it became red-hot. Preece's formula relates the filament current to the diameter of the conductor d for various materials: where K is a tabular constant approximately equal to 80 for copper. Using the ratio of the area of a circle, we can rewrite this formula for the case of a copper conductor with cross-sectional area S: In Preece's experiment, the conductor was suspended in the air, unlike a conductor on a printed circuit board, for which the heat dissipation conditions are completely different. The heat dissipation conditions are closer for the cases of a single connecting conductor, as well as for some cases of microwire welding (when compounding is not used to protect it), where this formula can give a good estimate for the limiting current. An acceptable increase in the temperature of the printed track is usually considered to be 10-30 ˚С. This value may be higher depending on the project parameters, however, over the entire range of operating temperatures of the product, the track temperature should be less than the glass transition temperature of the printed circuit board material (English glass transition temperature, Tg), and even more so the incandescence temperature of copper. Therefore, the dependence of the temperature increase ∆T on the current I of the printed track with width w and foil thickness h, given by D. Brooks in [1], is useful:
where C, α, β, γ are constants, the values of which for the outer and inner layers are given in Table 1. It is worth considering that on the outer layers the thickness of the foil is usually 20-40 microns greater than the base value due to additional sputtering when creating transitional layers holes. Also, the impact of the finish on boards without a mask can be significant. This is used in power devices, when additional solder is soldered onto the printed track exposed from the mask.
Another well-known formula for calculating the maximum current-carrying capacity of a conductor is the Onderdonk formula (English: IMOnderdonk), which contains such an important parameter as time. It relates the time t of passing current I through a copper conductor with cross-section S and the temperature increase ∆T relative to the initial temperature T0: Since the derivation of formula [2] excludes any heat removal, then for the case of a printed track this formula is applicable for a short current pulse with a duration of up to 1- 2 seconds. With increasing time and the influence of the heat sink, the accuracy of the estimate decreases, underestimating the limiting current by several times. Dependency graphs for all three given formulas for various parameters of the printed track are shown in Figures 1 and 2.
It is always important to take into account the experimental conditions or analytical assumptions when making a conclusion in order to understand the limits of applicability of a particular formula. None of the above formulas will give an accurate and optimal relationship between the limiting current and the required conductor cross-section for real applications. The same applies to simple calculators that can be found on the Internet (for example), because they are based on these or similar formulas. The influence of neighboring conductors and components as sources and receivers of heat, radiation, active or passive cooling can only be taken into account during thermoelectric modeling in specialized CAD systems (such as Cadence, ANSYS and others). However, even in this case, the results of simulation and experiment may differ significantly. The fact is that the printed track does not have a rectangular cross-section, but is close to trapezoidal (Fig. 3), and its width and the conductivity value of copper foil may not only differ from those calculated by the model, but also have some scatter from sample to sample, batch to batch, manufacturer to manufacturer, etc. The influence of width deviations increases as it decreases. However, the calculated results from the formulas and the recommendations of the standards will most often represent the worst case, thereby providing a margin of safety for the system. If the designer needs to optimize the relationship between the limiting current and the required cross-section of the printed track, then this goal must be achieved iteratively through modeling and experiment.
Skin effect
Increasing the cross-section of the printed track proportionally reduces its ohmic resistance per unit length, which reduces heat losses when direct current flows. The situation with alternating current is not so simple due to the existence of the skin effect, which leads to the fact that the alternating current density is unevenly distributed over the cross-section of the conductor, decreasing exponentially to zero from the surface of the conductor to the center. For the convenience of calculations, the concept of an effective cross-section of a conductor with a depth determined by the relation is used: where f is the frequency of the current, σ is the conductivity of the metal, μ is the magnetic permeability. At a depth equal to δ, the current density becomes e times less relative to the current density on the surface JS. Mathematically, it is possible to show the validity of the following approximate equality for the current density J(x,y) in a conductor: That is, for approximate calculations, it can be assumed that the current flows only in the boundary layer of a conductor of perimeter l with depth δ, and with a uniform distribution (Fig. 4).
Within this simplified model, if the depth of the surface layer is less than half the thickness of the printed track, then the impedance of the printed track at a given frequency will be determined by this effective cross section, leading to an increase in ohmic resistance and a slight decrease in inductance. In Fig. Figure 5 shows the dependence of the surface layer depth on the current frequency, taking into account the spread in the conductivity of the deposited copper. It shows that for copper layers with a thickness of 18 microns, the cutoff frequency (above which the skin effect plays a role) is in the region of 50-70 MHz, and for layers with a thickness of 35 microns - in the region of 15-20 MHz. Note that at frequencies above 100 MHz, the depth of the skin effect changes insignificantly, this allows us to neglect its dependence on frequency when calculating for high-frequency signals.
When designing printed circuit boards with constant currents of several amperes, it is necessary to perform thermal calculations for both electrical components and conductors. The presented models and analytical relationships make it possible to estimate the maximum current of printed tracks and, on its basis, select the required thickness of copper layers and the topology of the conductors. To obtain an accurate solution, it is necessary to use specialized CAD systems, and it is advisable to specify the geometry taking into account technological manufacturing errors and copper conductivity data obtained from the printed circuit board manufacturer. I highly recommend that you read the articles by D. Brooks devoted to a detailed analysis of methods for assessing the temperature of printed conductors, where visual results of modeling temperature fields are presented.
Literature
[1] Brooks DG, Adam J. "Trace Currents and Temperatures Revisited", UltraCAD, 2015. [2] Adam J., Brooks DG "In Search For Preece and Onderdonk", UltraCAD, 2015. The article
was first published in the journal " Components and technologies" 2022, No. 1. Publication on “Geektimes” has been approved by the editors of the magazine.
Heat transfer conditions
An important condition for heat transfer is the humid environment in which the cable is located. When placing a wire in the ground, heat removal is directly related to the structure and its composition, as well as the level of humidity.
To obtain the most accurate values, you will have to analyze the composition of the soil, depending on which the resistance will vary. Using the table, look for resistivity. Thanks to high-quality compaction, this characteristic can be reduced. Sand and gravel have lower thermal conductivity compared to clay, so ideally the wires are buried last. Instead of clay, you can use loam without admixtures of slag, stones and debris.
The heat dissipation of the air cable is minimal. The parameter decreases for lines in cable ducts that have an air gap. Cables located close to each other heat each other, so current loads should be kept as low as possible. Permissible currents are calculated using two different formulas depending on the operating mode - emergency or long-term. If a short circuit occurs, the permissible temperature for a paper-insulated wire is 200, PVC - 120 degrees Celsius.
It is important to remember the different cooling conditions for cables with and without insulation. In the first case, the heat flows emanating from the heating of the cores are forced to overcome an additional barrier in the form of an insulating layer.
Cable location in trench
When laying cables underground, when two conductors are located in one trench at once, the cooling process will slow down significantly, which will lead to a reduction in permissible current loads.
From the point of view of electrical and fire safety, determining the correct long-term permissible current and cable cross-section is an important condition to prevent overheating, insulation failure and ignition of the cable line. When making calculations, you should be careful and take into account many additional conditions. Certain adjustments are needed even for tabular values.
About high frequency current density
The current density of high frequencies (television and radio signals, for example) is calculated taking into account the so-called skin effect (skin - “skin” in English). Its essence is that the electromagnetic field pushes the current toward the surface of the wire, so to obtain the required density, you have to take a larger diameter of the wire, and in order not to waste extra copper, make it hollow, in the form of a tube.
The skin effect is important not only when transmitting high powers. If, for example, you wire cable television throughout your apartment with a coaxial cable that is too thin, then the losses in it due to the skin effect in the internal wire may be excessively large. Analog channels will ripple, and digital channels will crumble into squares.
The depth of the skin effect depends on the frequency of the signal, and the current density gradually drops to zero in the center of the wire. In technology, to simplify calculations, the depth of the skin surface is considered where the current density drops by 2.72 times compared to the surface density (Pos. 2 in the figure). The value 2.72 is derived in technical electrodynamics from the relationship between the electric and magnetic constants, which simplifies calculations.