Electrical parameters are studied as part of school programs. After exams, scientific definitions and formulas are quickly forgotten. Meanwhile, basic knowledge in the relevant field is needed not only by specialists and radio amateurs. They will be useful to ordinary users for connecting household appliances and solving other practical problems. This publication explains what a unit of current is.
Classic definition of current strength
Movement of charge along a conductor
As you already know, electric current is the ordered movement of charged particles. We say that particles are “charged” - this means that they have a certain charge $q$.
Accordingly, when such particles move, a certain charge is transferred. Each free electron in a metal carries a charge. Each ion in a solution of acids, salts or alkalis also carries a charge.
It is logical that the more particles move from one section of the chain to another, the greater the total charge they will transfer.
What determines the intensity of the action of electric current? It has been experimentally proven that the intensity (degree of action) of the electric current depends precisely on the magnitude of this transferred charge .
Basic electrical quantities
Electric current (I) is the directional movement of electric charges (ions in electrolytes, conduction electrons in metals). A necessary condition for the flow of electric current is the closed circuit. Electrical current is measured in amperes (A). The derived units of current are: 1 kiloampere (kA) = 1000 A; 1 milliamp (mA) 0.001 A; 1 microampere (μA) = 0.000001 A. A person begins to feel a current of 0.005 A passing through his body. A current greater than 0.05 A is dangerous to human life. Electric voltage (U) is the potential difference between two points in the electric field. The unit of electrical potential difference is the volt (V). 1 V = (1 W) : (1 A). The derived units of voltage are: 1 kilovolt (kV) = 1000 V; 1 millivolt (mV) = 0.001 V; 1 microvolt (μV) = 0.00000 1 V. The resistance of a section of an electrical circuit is a value that depends on the material of the conductor, its length and cross-section. Electrical resistance is measured in ohms (ohms). 1 Ohm = (1 V) : (1 A). Derived units of resistance are: 1 kiloohm (kOhm) = 1000 Ohm; 1 megaohm (MΩ) = 1,000,000 ohms; 1 milliOhm (mOhm) = 0.001 Ohm; 1 microOhm (µOhm) = 0.00000 1 Ohm. The electrical resistance of the human body, depending on a number of conditions, ranges from 2000 to 10,000 Ohms. Electrical resistivity (ρ) is the resistance of a wire with a length of 1 m and a cross-section of 1 mm2 at a temperature of 20 °C. The reciprocal of resistivity is called electrical conductivity (γ). Power (P) is a quantity that characterizes the speed at which energy is converted, or the speed at which work is done. Generator power is a quantity that characterizes the rate at which mechanical or other energy is converted into electrical energy in the generator. Consumer power is a quantity that characterizes the speed at which electrical energy is converted in individual sections of the circuit into other useful types of energy.
The SI system unit of power is the watt (W). It is equal to the power at which 1 joule of work is performed in 1 second: 1 W = 1 J/1 sec The derived units of electrical power are: 1 kilowatt (kW) = 1000 W; 1 megawatt (MW) = 1000 kW = 1,000,000 W; 1 milliwatt (mW) = 0.001 W; o1i 1 horsepower (hp) = 736 W = 0.736 kW. The units of electrical energy are: 1 watt-second (W sec) = 1 J = (1 N) (1 m); 1 kilowatt-hour (kW h) = 3.6 106 W sec. Example. The current consumed by an electric motor connected to a 220 V network was 10 A for 15 minutes. Determine the energy consumed by the motor. W*sec, or dividing this value by 1000 and 3600, we get energy in kilowatt-hours: W = 1980000/(1000*3600) = 0.55 kWh
Let's consider the basic electrical quantities that we study first at school, then in secondary and higher educational institutions. For convenience, we will summarize all the data in a small table. Definitions of individual quantities will be given after the table in case of any misunderstandings.
Current strength
The electric charge passing through the cross section of the conductor in $1 \space c$ will determine such a value as the current strength in the circuit (Figure 1).
Figure 1. Charge passing through a cross-section of a conductor
Current strength is a physical quantity equal to the ratio of the electric charge $q$ passing through the cross section of the conductor to the time of its passage $t$: $I = \frac{q}{t}$, where $I$ is the current strength.
Kilowatt and kilowatt-hour - what's the difference?
Along with the designation kilowatt, you can find the unit kilowatt per hour. For example, electricity meter readings are displayed in kWh values. Non-specialists do not distinguish between these concepts and believe that they are one and the same thing. However, these are completely different quantities.
Watt per hour is the amount of electricity produced or consumed per unit of time, denoted Wh.
For example, 1 kW hour means that the power receiver consumes 1 kW of electricity in 1 hour.
Kilowatt, unlike kWh, is a quantity indicating instantaneous power consumed or generated.
The force of interaction between conductors and current as the basis for determining the unit of current
In order to determine the unit of measurement of current strength, experiments were carried out, which we will now consider. These experiments consisted of the phenomenon of interaction of two conductors with current.
Let's take two flexible straight conductors. Let's place them parallel to each other. Let's connect them to a current source (Figure 2).
Figure 2. Interaction of conductors with current
Once the circuit is closed, an electric current will flow through it. The current will also flow through our experimental conductors.
What will we see? They will begin to interact with each other. Namely, they will be attracted to each other (Figure 2, a) or repelled from each other (Figure 2, b). This will depend on the direction of the current in them.
The question immediately arises of how to measure this force with which the conductors interact? Experiments have shown the following.
The strength of interaction between conductors with current depends on: the length of the conductors; distances between them; the environment in which the conductors are located; current strength in conductors .
For us now the very last point is important. Let's take conductors for which all other conditions will be the same, except for the strength of the currents. It turns out that the greater the current in each conductor, the greater the force they interact with each other.
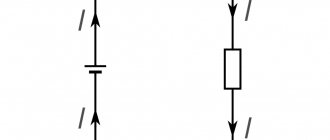
Electrical voltage in the circuit
Voltage sources in circuits typically use one of the following symbols.
Voltage sources and electrical circuit
The voltage source always has two connections/poles. A plus pole and a minus pole. The voltage itself is indicated by a voltage arrow (UQ). For sources it is always displayed from plus to minus.
The electrical voltage dropped across a resistor can also be indicated by a voltage arrow (indicated in the diagram as a red arrow UR). This indicates the technical direction of the electric current.
You can also often hear the term “open circuit voltage” or “source voltage”. This is the output voltage of an unloaded source, i.e. source to which nothing is connected. If the circuit is closed with a load, then only the voltage at the source poles can be measured.
Current unit
Now imagine very thin and very long conductors. They are located parallel to each other. The distance between them is $1 \space m$. The current strength in them is the same. And all this in a vacuum! This is where the unit of current measurement comes in (Figure 3).
As a unit of current strength, I take the current strength at which segments of parallel conductors of length $1 \space m$ interact with a force of $2 \cdot 10^{-7} \space Н$ ($0.0000002 \space Н$).
Figure 3. Defining the unit of current measurement
The name of this unit is ampere ($A$) . It is named after the French physicist Andre Ampère (Figure 4).
Figure 4. Ampere Andre Marie (1775 - 1836) - French physicist, mathematician and natural scientist. He introduced the concept of electric current into physics, for which he was nicknamed “the Newton of electricity” in the scientific community.
Basic units of measurement in the SI system| Length | meter | m | m |
| Weight | kilogram | kg | kg |
| Time | second | With | s |
| Electric current strength | ampere | A | A |
| Thermodynamic temperature | kelvin | TO | K |
| Quantity of substance | mole | mole | mol |
| The power of light | candela | cd | CD |
| Flat angle | radian | glad | rad |
| Solid angle | steradian | Wed | sr |
Definitions of SI major and supplementary units
Meter
equal to the length of the path traveled by light in a vacuum during a time interval of 1/299,792,458 seconds.
Kilogram
equal to the mass of the international prototype kilogram.
Second
equal to 9,192,631,770 periods of radiation corresponding to the transition between two hyperfine levels of the ground state of the cesium-133 atom.
Ampere
is equal to the strength of a constant current, which, when passing through two parallel conductors of infinite length and negligibly small circular cross-sectional area, located in a vacuum at a distance of 1 m from each other, would cause an interaction force equal to 2 * 10 -7 N.
Kelvin
equal to 1/273.16 of the thermodynamic temperature of the triple point of water.
Mole
equal to the amount of substance in a system containing the same number of structural elements as there are atoms in carbon-12 weighing 0.012 kg.
Candela
equal to the luminous intensity in a given direction of a source emitting monochromatic radiation with a frequency of 540*1012 Hz, the luminous energy intensity of which in this direction is 1/683 W/sr.
Radian
is equal to the angle between two radii of a circle, the length of the arc between which is equal to the radius.
Steradian
is equal to the solid angle with the vertex at the center of the sphere, cutting out on the surface of the sphere an area equal to the area of a square with a side equal to the radius of the sphere.
Derived units of electrical and magnetic quantities in the SI system
| Name of quantity | Unit | ||
| Name | Designation | ||
| Russian | international | ||
| Electric current density | ampere per square meter | A/m2 | A/m2 |
| Amount of electricity; electric charge | pendant | Cl | C |
| Surface electric charge density | pendant per square meter | C/m2 | C/m2 |
| Electrical voltage; electric potential, electric potential difference; EMF | volt | IN | V |
| Electric field strength | volt per meter | V/m | V/m |
| Electrical capacity | farad | F | F |
| Absolute dielectric constant; dielectric constant | farad per meter | F/m | F/m |
| Electrical resistance | ohm | Ohm | W |
| Electrical resistivity | ohm meter | Ohm.m | Wm |
| Electrical conductivity | Siemens | Cm | S |
| Electrical conductivity | siemens per meter | Sm/m | S/m |
| Magnetic flux | weber | Wb | Wb |
| Magnetic induction | tesla | Tl | T |
| Inductance | Henry | Gn | H |
| Absolute magnetic permeability; magnetic constant | henry per meter | Gn/m | H/m |
| Energy | joule | J | J |
| Active power | watt | W | W |
| Full power | volt-ampere | V.A | V.A. |
Multipliers and prefixes in the SI system
| Console | Prefix designation | Factor | Changing the multiplier | |
| Russian | international | |||
| exa | E | E | 1018=1000000000000000000 | quintillion |
| peta | P | P | 1015=1000000000000000 | quadrillion |
| tera | T | T | 1012=1000000000000 | trillion |
| giga | G | G | 109=1000000000 | billion |
| mega | M | M | 106=1000000 | million |
| kilo | To | k | 103=1000 | thousand |
| hecto | G | h | 102=100 | one hundred |
| soundboard | Yes | da | 101=10 | ten |
| — | — | — | 100=1 | unit |
| deci | d | d | 10-1=0,1 | one tenth |
| centi | With | c | 10-2=0,01 | one hundredth |
| Milli | m | m | 10-3=0,001 | one thousandth |
| micro | mk | m | 10-6=0,000001 | one millionth |
| nano | n | n | 10-9=0,000000001 | one billionth |
| pico | P | p | 10-12=0,000000000001 | one trillionth |
| femto | f | f | 10-15=0,000000000000001 | one quadrillionth |
| atto | A | a | 10-18=0,000000000000000001 | one quintillionth |
Example
: 1 µW=0.000001 W=1000 nW
Origin of the names of SI prefixes
The first prefixes were introduced in 1793-1795. with the legalization of the metric system of measures in France. It was customary to take the names of prefixes for multiple units from Greek, and for submultiples - from Latin. In those years the following prefixes were adopted: kilo...
(from the Greek chilioi - one thousand),
hecto...
(from the Greek hekaton - one hundred),
deka...
(from the Greek deka - ten),
deci...
(from the Latin decem - ten),
centi...
(from the Latin centum - hundred),
milli...
(from Latin mille - thousand).
In subsequent years, the number of multiples and submultiples increased; the names of the prefixes to designate them were sometimes borrowed from other languages. The following prefixes appeared: mega...
(from the Greek megas - big),
giga...
(from the Greek gigas, gigantos - giant),
tera...
(from the Greek teras, teratos - huge, monster),
micro...
(from the Greek mikros - small, small),
nano...
(from Greek nanos - dwarf),
pico...
(from Italian piccolo - small, small),
femto...
(from Danish femten - fifteen),
atto...
(from Danish atten - eighteen ).
The last two prefixes peta...
and
exa...
- were adopted in 1975:
"peta"
... (from the Greek peta - five, which corresponds to five digits of 10 3),
"exa"
... (from the Greek hex - six, which corresponds to six categories of 10 3).
Current strength of some electrical appliances
For a better understanding of how much one ampere is in practice, Table 1 shows the average current values for some electrical appliances.
| Device | Current value $I$, A |
| Flashlight bulb | 0,1 |
| Regular incandescent lamp | 0,3 — 0,5 |
| Fridge | 0,8 — 1 |
| TV | 1,2 — 2 |
| Electric iron | 3 |
| Vacuum cleaner | 4 — 9 |
| Washing machine | 6 — 10 |
| Trolleybus engine | 160 — 220 |
| Lightning | more than 400,000 |
Table 1. Current values in various electricity consumers
Relationship between charge unit and current unit
Although we have already talked about charge and its unit of measurement (coulomb) earlier, in physics it is customary to define it in terms of ampere.
Let us express the charge itself from the definition of current ($I = \frac{q}{t}$) and obtain the following formula.
$q = It$.
If $I = 1 \space A$, and $t = 1 \space c$, then we get a unit of electric charge - $1 \space Cl$.
$1 \space pendant = 1 \space ampere \cdot 1 \space s$, or $1 \space Cl = 1 \space A \cdot 1 \space s = 1 \space A \cdot s$.
A unit of electric charge is taken to be the electric charge passing through the cross section of a conductor at a current strength of $1 \space A$ for a time of $1 \space s$.
Electrical voltages for series and parallel connections
We already have an article on series and parallel connection of conductors in which we discuss this topic in more detail. So here we'll just cover some of the basics.
In a series connection, components are connected in a row.
Electrical voltage in series connection
Here the electrical voltage of the source is divided into resistors. This point is also described by Kirchhoff's second rule. The following applies here:
UQ = U1 + U2 + U3
that is, the source voltage is equal to the sum of the electrical voltages across the individual resistors. The source voltage is distributed differently across different resistors.
In an electrical circuit with a parallel connection, the components are arranged in parallel relative to each other. This can be seen in the following diagram.
Electrical voltage in a parallel circuit
Here it is much easier to determine the electrical voltages on the resistors, since with a parallel connection:
UQ = U1 = U2 = U3
Therefore, the electrical voltage across the resistors is as high as the electrical voltage of the source.
Electric charge and its dependence on current and time
We have obtained a formula that allows us to take a fresh look at the definition of electric charge: $q = It$.
We conclude: the electric charge passing through the cross section of the conductor depends on the strength of the current and the time of its passage.
This knowledge will be useful in solving problems. Note that electric charge is sometimes called quantity of electricity .
For example, let's find the amount of electricity that passes through the cross section of the lamp's spiral in $1 \space min$. The lamp current is $400 \space mA$.
Given: $I = 400 \space mA$ $t = 1 \space min$
SI: $I = 0.4 \space A$ $t = 60 \space s$
$q — ?$
Show solution and answer
Hide
Solution:
We use the formula for electric charge obtained from the definition of current: $q = It$.
Let's calculate this charge: $q = 0.4 \space A \cdot 60 \space c = 24 \space Cl$.
Answer: $q = 24 \space Cl$.
What is AC
The translation of the abbreviation AC from English means Alternative Current. Accordingly, DC, which is read as Direct Current, denotes a constant voltage flowing in one direction. Each is used to power electrical appliances and plays a key role in the integrity of electrical equipment if not properly connected.
Healthy! An electric current that does not change its magnitude and direction over time is called constant.
Alternating current is the form widely used by consumers to ensure the functionality of essential electrical equipment. Mostly the standard waveform in electrical circuits is presented in the form of a sinusoidal curve, with a positive half-cycle equal to the positive voltage flow and vice versa.
In some cases, for example, music amplifiers, different waveforms are used. They can be triangular or rectangular. Audio and radio signals transmitted over wires also refer to alternating current. This type of voltage carries encrypted information data (sounds or images). In some cases, transmission can be carried out through modulation. This current predominantly alternates with high-frequency currents, which distinguishes them from conventional electricity transmission.
Exercises
Exercise No. 1
Express in amperes the current equal to $2000 \space mA$;
$100 \space mA$; $55 \space mA$; $3 \space ka$. Given: $I_1 = 2000 \space mA$ $I_2 = 100 \space mA$ $I_3 = 55 \space mA$ $I_4 = 3 \space kA$
Show solution and answer
Hide
Solution:
$I_1 = 2000 \space mA = 2000 \cdot 10^{-3} \space A = 2 \space A$.
$I_2 = 100 \space mA = 100 \cdot 10^{-3} \space A = 0.1 \space A$.
$I_3 = 55 \space mA = 55 \cdot 10^{-3} \space A = 0.055 \space A$.
$I_4 = 3 \space kA = 3 \cdot 10^3 \space A = 3000 \space A$.
Answer: $I_1 = 2 \space A$, $I_2 = 0.1 \space A$, $I_3 = 0.55 \space A$, $I_4 = 3000 \space A$.
Exercise No. 2
The current strength in the electric stove circuit is $1.4 \space A$.
What electric charge passes through the cross section of its spiral in $10 \space min$? Given: $t = 10 \space min$ $I = 1.4 \space A$
SI: $t = 600 \space s$
$q — ?$
Show solution and answer
Hide
Solution:
We use the formula: $q = It$. $q = 1.4 \space A \cdot 600 \space c = 840 \space Cl$.
Answer: $q = 840 \space Kl$.
Electrical voltage measurement
Voltage measuring instruments, also called voltmeters, are always connected in parallel to the consumer on which the electrical voltage needs to be measured.
One of the most commonly used voltmeters is the digital multimeter (DMM), so we will show you the procedure for measuring voltage using a DMM. First you need to set the type of electrical voltage (DC - direct current or AC - alternating current).
For direct current it is necessary to pay attention to the correct polarity, i.e. connect the plus to the positive pole. The next step is to select the correct measuring range. If you can't estimate how big the quantity you're measuring is, set the range to the largest possible and work down from there until you find the right one. Finally, you only need to “read” the electrical voltage as an instrument.