4.7
Average rating: 4.7
Total ratings received: 248.
4.7
Average rating: 4.7
Total ratings received: 248.
A change in the magnetic field that penetrates the frame with current causes the appearance of an electromotive force (EMF) in it, and a current arises in the frame. The direction of this current is determined by Lenz's special rule for the law of electromagnetic induction. Let's look at this rule.
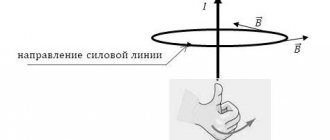
Lenz's experience
To answer the questions asked, the following experiment is carried out. At the ends of the easily rotating rocker arm, two conductive rings are fixed - one solid and the other with a cut.
Rice. 1. An experiment demonstrating Lenz’s rule.
Now, if you take a permanent magnet and insert it into a ring with a cut, nothing will happen. However, if you try to insert a permanent magnet into a solid ring, the rocker arm will begin to rotate, moving the ring away from the magnet.
This phenomenon can only be explained by the occurrence of current in a solid ring. This current, in turn, generates a new magnetic field, which begins to interact with the field of the permanent magnet. In a ring with a cut, no current arises and there is no interacting field.
Formulation
Lenz's rule is usually formulated as follows:
The induced current always has such a direction that it weakens the effect of the cause that excites this current.
Wikipedia
Let's decipher this sentence.
Let's decipher this sentence. Let's start with the reason. The reason for the flow of induced current is the changing flux of magnetic induction B through the surface covered by the circuit in which the electric current must flow.
The counteracting reason here is that when the flux increases, the magnetic field Bind created by the induced current is directed to reduce the flux. Conversely, when the flux decreases, the induced magnetic field is directed to increase the flux. In general, if the field B is perpendicular to a flat surface enclosing a closed conductor, then
When ФB decreases, then Bind is parallel to B. When ФB increases, then Bind is antiparallel to B.
In a more general case, it is necessary to specify a condition for the angles between these vectors.
Once we have established the direction of the magnetic induction vector Bind (inside the loop), we must associate the induced current with this vector and determine its direction.
Lenz's rule
Carrying out the described experiment, the Russian physicist E. Lenz derived a rule that determines the direction of the induced current in a conducting circuit.
Rice. 2. E. Lenz.
the induced current arising in a closed circuit is directed so as to counteract the cause that causes it.
Applying Lenz's rule to determine the direction of the induced current involves the following steps.
- Using the magnetic flux formula $Ф=BScos\alpha$, it is determined how the magnetic flux through the circuit changes - whether it increases or decreases.
- The direction of the resulting induction is determined. It, according to Lenz's rule, must be directed in such a way as to counteract the cause that causes it. That is, if the magnetic flux increases, then the resulting induction should be directed against the external induction, if the flux decreases, then along.
- The direction of the induction current is determined by the gimlet rule or the rule of reaching the right hand.
Lenz's rule is determined by the law of conservation of energy. Since a current arises in the circuit, it does work (all of it goes to heating the ring), and this work can only arise due to external forces. In Lenz's experiment, such forces are mechanical forces that introduce a magnet into the ring, thereby doing work.
If, for the Lenz experiment, we take a superconducting plate (at very low temperatures) that has no resistance, and place a magnet below, then the induced emf will create a current of such strength that its magnetic field will not allow the plate to approach the magnet, the plate will be able to float in the air, above the magnet without going down.
Rice. 3. Levitation of a superconductor plate above a magnet.
Electromagnetic induction
Electromagnetic induction is the phenomenon of the occurrence of current in a closed conducting circuit when the magnetic flux passing through it changes.
The phenomenon of electromagnetic induction was discovered by M. Faraday.
Michael Faraday conducted a series of experiments that helped discover the phenomenon of electromagnetic induction.
Experience once. Two coils were wound on one non-conducting base: the turns of the first coil were located between the turns of the second. The turns of one coil were closed to a galvanometer, and the second was connected to a current source.
When the key was closed and current flowed through the second coil, a current pulse arose in the first. When the switch was opened, a current pulse was also observed, but the current through the galvanometer flowed in the opposite direction.
Experience two. The first coil was connected to a current source, and the second to a galvanometer. In this case, the second coil moved relative to the first. As the coil approached or moved away, the current was recorded.
Experience three. The coil is closed to the galvanometer, and the magnet moves in (extends) relative to the coil
Here's what these experiments showed:
- Induction current occurs only when the lines of magnetic induction change.
- The direction of the current will be different when the number of lines increases and when they decrease.
- The strength of the induction current depends on the rate of change of the magnetic flux. The field itself may change, or the circuit may move in a non-uniform magnetic field.
| Why does induced current occur? Current in a circuit can exist when external forces act on free charges. The work done by these forces to move a single positive charge along a closed loop is equal to the emf. This means that when the number of magnetic lines through the surface limited by the contour changes, an emf appears in it, which is called the induced emf. |
Online physics courses at Skysmart are no less exciting than our articles!
Self-induction
Self-induction is the phenomenon of the occurrence of induced emf in a conductor as a result of a change in current in it.
When the current in the coil changes, the magnetic flux created by this current changes. A change in the magnetic flux passing through the coil should cause the appearance of an induced emf in the coil.
In accordance with Lenz's rule, the self-inductive emf prevents the current from increasing when the circuit is turned on and the current from decreasing when the circuit is turned off.
This leads to the fact that when a circuit is closed in which there is a current source with a constant EMF, the current strength is established after some time.
When the source is turned off, the current also does not stop instantly. The self-inductive emf that arises in this case may exceed the source emf.
The phenomenon of self-induction can be observed by assembling an electrical circuit from a coil with high inductance, a resistor, two identical incandescent lamps and a current source. The resistor must have the same electrical resistance as the coil wire.
Experience shows that when the circuit is closed, an electric lamp connected in series with a coil lights up somewhat later than a lamp connected in series with a resistor. The increase in current in the coil circuit during closure is prevented by the self-induction emf, which occurs when the magnetic flux in the coil increases.
When the power source is turned off, both lamps flash. In this case, the current in the circuit is maintained by the self-induction emf that occurs when the magnetic flux in the coil decreases.
Self-induction emf ( varepsilon_{is} ), arising in a coil with inductance ( L ), according to the law of electromagnetic induction is equal to:
The self-inductive emf is directly proportional to the inductance of the coil and the rate of change of current in the coil.
Application of the Joule-Lenz law in life
The discovery of the Joule-Lenz law had enormous consequences for the practical applications of electric current. Already in the 19th century, it became possible to create more accurate measuring instruments based on the contraction of a wire spiral when heated by a flowing current of a certain magnitude - the first dial voltmeters and ammeters. The first prototypes of electric heaters, toasters, and melting furnaces appeared - a conductor with a high resistivity was used, which made it possible to obtain a fairly high temperature.
Fuses and bimetallic circuit breakers (analogs of modern thermal protection relays) were invented, based on the difference in heating of conductors with different resistivities. And, of course, having discovered that at a certain current strength, a conductor with high resistivity can heat up red-hot, this effect was used as a light source. The first light bulbs appeared.
A conductor (carbon stick, bamboo thread, platinum wire, etc.) was placed in a glass flask, air was pumped out to slow down the oxidation process and an undamped, clean and stable light source was obtained - an electric light bulb
Faraday-Maxwell law
In 1873, J.C. Maxwell presented a new theory of the electromagnetic field. The equations he derived formed the basis of modern radio engineering and electrical engineering. They are expressed as follows:
- Edl = -dФ/dt – electromotive force equation
- Hdl = -dN/dt – equation of magnetomotive force.
Where E is the electric field strength in the area dl; H – magnetic field strength in section dl; N is the flow of electrical induction, t is time.
The symmetrical nature of these equations establishes a connection between electrical and magnetic phenomena, as well as magnetic and electrical. the physical meaning that defines these equations can be expressed by the following provisions:
- if the electric field changes, then this change is always accompanied by a magnetic field.
- if the magnetic field changes, then this change is always accompanied by an electric field.
Rice. 3. Emergence of a vortex magnetic field
Maxwell also established that the propagation of the electromagnetic field is equal to the speed of propagation of light.
Why does the conductor get hot?
How is the heating of the conductor explained? Why does it heat up and not remain neutral or cool down? Heating occurs due to the fact that free electrons moving in a conductor under the influence of an electric field bombard the atoms of metal molecules, thereby transferring to them their own energy, which turns into heat. To put it quite simply: when overcoming the material of the conductor, the electric current seems to “rub”, colliding with electrons against the molecules of the conductor. Well, as you know, any friction is accompanied by heating. Consequently, the conductor will heat up while electric current runs through it.
It also follows from the formula that the higher the resistivity of the conductor and the higher the current flowing through it, the higher the heating will be. For example, if you connect a copper conductor (resistivity 0.018 Ohm mm²/m) and an aluminum conductor (0.027 Ohm mm²/m) in series, then when electric current flows through the circuit, aluminum will heat up more than copper due to its higher resistance . Therefore, by the way, it is not recommended to twist copper and aluminum wires together in everyday life - there will be uneven heating at the point of twisting. The result is burning with subsequent loss of contact.