OGE 2022 in physics ›
1. Electric current, passing through a circuit, produces different effects: thermal, mechanical, chemical, magnetic. In this case, the electric field does work, and electrical energy is converted into other types of energy: internal, mechanical, magnetic field energy, etc.
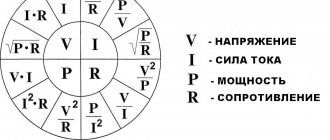
As has been shown, the voltage \( (U) \) in a section of the circuit is equal to the ratio of the work \( (F) \) performed when moving an electric charge \( (q) \) in this section to the charge : \( U=A/q \). Hence \( A=qU \). Since the charge is equal to the product of current \( (I) \) and time \( (t) \) \( q=It \), then \( A=IUt \), i.e. . The work done by an electric current on a section of a circuit is equal to the product of the voltage on that section, the current strength and the time during which the work is performed.
The unit of work is the joule (1 J) . This unit can be expressed in terms of electrical units:
\( [A] \)= 1 J = 1 V · 1 A · 1 s
To measure work, three measuring instruments are used: ammeter, voltmeter and clock, however, in real life, electric energy meters are used to measure the work of electric current.
If you need to find the work done by a current, but the current strength or voltage is unknown, then you can use Ohm’s law, express the unknown quantities and calculate the work using the formulas: \( A=\frac{U^2}{R}t \) or \( A=I^2Rt \).
2. The power of the electric current is equal to the ratio of the work to the time during which it was completed: \( P=A/t \) or \( P=IUt/t \); \( P=IU \) , i.e. The power of the electric current is equal to the product of voltage and current in the circuit .
The unit of power is the watt (1 W): \( [P]=[I]\cdot[U] \); \( [P] \) = 1 A · 1 V = 1 W.
Using Ohm's law, you can obtain other formulas for calculating current power: \( P=\frac{U^2}{R};P=I^2R \).
The power of the electric current in a conductor can be determined using an ammeter and a voltmeter by measuring the current and voltage, respectively. To measure power, you can use a special device called a wattmeter, which combines an ammeter and a voltmeter.
3. When electric current passes through a conductor, it heats up. This happens because free electrons in metals and ions in electrolyte solutions moving under the influence of an electric field collide with molecules or atoms of conductors and transfer their energy to them. Thus, when work is done by the current, the internal energy of the conductor increases, a certain amount of heat is released in it, equal to the work done by the current, and the conductor heats up: \( Q=A \) or \( Q=IUt \). Considering that \( U=IR \), \( Q=I^2Rt \).
The amount of heat released when current passes through a conductor is equal to the product of the square of the current strength, the resistance of the conductor and time.
This law is called the Joule-Lenz law.
What is current work
With the chaotic movement of charged particles in a conductor, the electric field will perform work, which they decided to call the work of current. The definition of current work is as follows: it is the work of an electric field to transfer charges inside a conductor.
Important! In addition to electrical forces, magnetic forces also act on the conductor, which can also do work. However, under normal conditions it will be very small.
Movement of charges in a conductor
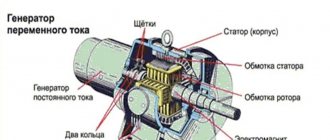
History of the discovery of alternating current
For the first time, alternating currents began to receive attention due to their commercial value after the inventions created by Nikola Tesla. The material conflict with Edison marked the fate of both. When the American entrepreneur took back his promises to Nikola Tesla, he lost considerable benefits. The outstanding scientist did not like the free treatment; the Serb invented an industrial-type AC motor (he made the invention much earlier). Enterprises used exclusively constant. Edison promoted the said species.
Tesla was the first to show that much greater results can be achieved with alternating voltage. Especially when energy has to be transmitted over long distances. The use of transformers can easily increase the voltage, sharply reducing losses on active resistance. The receiving side returns the parameters to the original ones. Save a lot on the thickness of the wires.
Today it has been shown that direct current transmission is more economically profitable. Tesla changed the course of history. If scientists had come up with DC-DC converters, the world would look different.
Nikola Tesla started the active use of alternating current by creating a two-phase motor. Experiences in transmitting energy over considerable distances have put the facts in their place: it is inconvenient to transfer production to the Niagara Falls area, it is much easier to lay a line to its destination.
School version of the interpretation of alternating and direct current
Alternating current exhibits a number of properties that distinguish the phenomenon from direct current. First, let us turn to the history of the discovery of the phenomenon. Otto von Guericke is considered the founder of alternating current in human use. He was the first to notice: natural charges have two signs. Current can flow in different directions. Regarding Tesla, the engineer was more interested in the practical part; the author’s lectures mention two experimenters of British origin:
- William Spottiswoode is deprived of a Russian-language Wikipedia page, the national part is silent about work with alternating current. Like Georg Ohm, the scientist is a talented mathematician; it remains to be regretted that it is difficult to find out what exactly the husband of science did.
- James Edward Henry Gordon is much closer to the practical part of the question of the use of electricity. He experimented a lot with generators and developed a device of his own design with a power of 350 kW. He paid a lot of attention to lighting and energy supply to plants and factories.
It is believed that the first alternating current generators were created in the 30s of the 19th century. Michael Faraday studied magnetic fields experimentally. The experiments aroused the jealousy of Sir Humphry Davy, who criticized the student for plagiarism. It is difficult for descendants to find out what is right, the fact remains: alternating current existed unclaimed for half a century. In the first half of the 19th century, the electric motor was invented (by Michael Faraday). Worked powered by direct current.
Nikola Tesla was the first to realize Arago's theory of a rotating magnetic field. Two phases of alternating current (90 degree shift) were required. Along the way, Tesla noted: more complex configurations are possible (text of the patent). Later, the inventor of the three-phase motor, Dolivo-Dobrovolsky, tried in vain to patent the brainchild of a fertile mind.
For a long time, alternating current remained unclaimed. Edison opposed the introduction of the phenomenon into everyday life. The industrialist was afraid of large financial losses.
Nikola Tesla studied electric machines
Units
Any physical quantity that can be converted into energy will be measured in Joules (J). 1 Joule is equal to the work done to move a point to which a force equal to 1 Newton is applied multiplied by a Path of 1 meter. It turns out that 1 J = 1 N · 1 m.
The unit of power is Watt (W). It is equal to 1 J of work done per unit of time of 1 s. Thus, 1 W = 1 J: 1 s
Power unit
Table of physical quantities and their description:
| DEFINITION | ||
| Ampere | A | Current strength |
| Watt | W | Power at which 1 joule of work is done in 1 second |
| Weber | Wb | Magnetic flux, when it decreases to zero, an amount of electricity of 1 coulomb flows in a circuit connected to it with a resistance of 1 ohm |
| Volt | V | Electrical voltage that causes a direct current of 1 ampere at a power of 1 watt in an electrical circuit |
| Time | t | a continuous quantity, an a priori characteristic of the world, not determined by anything. As a basis for measurement, a certain sequence of events is simply taken, about which it is considered undoubtedly true that it occurs at equal intervals of time |
| Henry | N | Henry can also be defined as the inductance of an electrical circuit in which an emf of 1 volt occurs when the current in the circuit changes at a rate of 1 ampere per second |
| Hertz | Нz | Frequency of a periodic process whose period is 1 second |
| Pressure | R | a physical quantity characterizing the state of a continuous medium and numerically equal to the force acting per unit surface area perpendicular to this surface |
| Joule | J | The work done by a force of 1 newton when it moves a body a distance of 1 meter in the direction of the force |
| Diameter | d | a segment connecting two points) on a circle (sphere, ball surface), and passing through the center of this circle (sphere, ball). The length of this segment is also called diameter. The diameter of a circle is the chord passing through its center; such a chord has a maximum length. The diameter is equal to two radii |
| Diopter | δ | A unit for measuring the optical power of spherical-concave glass, equal to the optical power of a lens with a focal length of 1 meter |
| Length | L | physical quantity, numerical characteristic of the length of lines. In a narrow sense, length refers to the size of an object in the longitudinal direction (usually this is the direction of the largest size), i.e., the distance between its two most distant points, measured horizontally |
| Pulse | R | a measure of mechanical movement; is a vector quantity, in classical mechanics equal for a material point to the product of the mass m of this point by its speed v and directed in the same way as the speed vector: |
| Inductance | L | coefficient of proportionality between the magnetic flux (created by the current of any turn in the absence of magnetizing media, for example, in air) and the magnitude of this current |
| Kilogram | kg | Mass of the platinum-iridium prototype approved by the international conference in Paris in 1889 |
| Pendant | With | The amount of electricity passing in 1 second at a current of 1 ampere through the cross-section of a conductor |
| Lumen | lm | Luminous flux emitted by a point source in a solid angle of 1 steradian at a luminous intensity of 1 candle |
| Lux | lx | Illumination of a surface that uniformly receives a luminous flux of 1 lumen per 1 square meter of area |
| Weight | M | one of the most important physical quantities. Initially (XVII-XIX centuries) it characterized the “amount of matter” in a physical object, on which, according to the ideas of that time, both the object’s ability to resist applied force and gravitational properties—weight |
| Meter | m | The old platinum-iridium meter standard (international prototype) is stored in the cellars of Sèvres |
| Square meter | m² | Area of a square whose side is 1 meter |
| Cubic meter | m³ | Volume of a cube with edge length equal to 1 meter |
| Meter per second | m/s | The speed of a moving body covering a distance of 1 meter per second |
| Power | R | a physical quantity equal to the ratio of work performed over a certain period of time to this period of time. |
| Newton | N | A force that imparts an acceleration of 1 meter per second to a body weighing 1 kilogram in the direction of the force. |
| Volume | m³, cm³, L³ | a quantitative characteristic of the space occupied by a body or substance. The volume of the body or the capacity of the vessel is determined by its shape and linear dimensions. The concept of capacity is closely related to the concept of volume. Capacity refers to the volume of the internal space of a vessel or apparatus, storage boxes, etc. |
| Ohm | Ω | The resistance of a conductor between the ends of which a voltage of 1 volt occurs at a current of 1 ampere. |
| Pascal | Pa | Pressure per square meter with a force of 1 newton |
| Square | S | One of the quantitative characteristics of flat geometric shapes and surfaces |
| Density | R | a physical quantity determined for a homogeneous substance by the mass of its unit volume. For an inhomogeneous substance, the density at a certain point is calculated as the limit of the ratio of the mass of the body (m) to its volume (V), when the volume contracts to this point |
| Radius | r | a segment connecting the center of a circle (or sphere) with any point lying on the circle (or surface of a sphere), as well as the length of this segment |
| Candle | CD | Candle is a unit of luminous intensity, the value of which is taken such that the brightness of the full emitter at the solidification temperature of platinum is equal to 60 candles per square centimeter |
| Candle per m² | cd/m² | The brightness of a luminous surface with an area of 1 square meter at a light intensity of 1 candle |
| Second | s | A minute is equal to 60 seconds, an hour is 3600 seconds, a day is 86400 seconds |
| Force | F | a vector physical quantity that is a measure of the intensity of interaction between bodies. A force applied to a massive body causes a change in its speed or the occurrence of deformations in it |
| The power of light | J | radiation flux per unit solid angle within which it propagates |
| Speed | ύ, u | a physical quantity characterizing the speed of movement and direction of movement of a material point in space relative to the selected reference system |
| Resistance (electrical) | R | a scalar physical quantity that characterizes the properties of a conductor and is equal to the ratio of the voltage at the ends of the conductor to the strength of the electric current flowing through it |
| Temperature | °C | a physical quantity that approximately characterizes the average kinetic energy of particles of a macroscopic system per one degree of freedom in a state of thermodynamic equilibrium. |
| Heat | Q | a measure of energy transferred from one body to another during the process of heat transfer. The SI unit of heat is the joule |
| Heat capacity | C, J/kg | heat capacity is the amount of heat required to heat a unit amount of a substance |
| Tesla | T | Magnetic induction, at which the magnetic flux through a cross-section of 1 square meter is equal to 1 weber |
| Current | I | in a conductor - a scalar quantity numerically equal to the charge flowing per unit time through the cross section of the conductor. |
| Frequency | F, f, ω | physical quantity, characteristic of a periodic process, equal to the number of complete cycles completed per unit of time |
| Farad | F | The capacitance of a capacitor between the plates of which a voltage of 1 volt appears when charged by 1 coulomb |
| Energy | E | a physical quantity that is a unified measure of various forms of motion of matter and a measure of the transition of the motion of matter from one form to another |
There are decimal prefixes that are used in the name of the quantity and serve to simplify the description. The most common of them are: mega, miles, kilo, nano, pico. The table shows other prefixes, except those mentioned.
| Decimal multiplier | Pronunciation | Designation (Russian/international) |
| 10-30 | cuecto | q |
| 10-27 | ronto | r |
| 10-24 | iocto | and/y |
| 10-21 | zepto | s/z |
| 10-18 | atto | a |
| 10-15 | femto | f/f |
| 10-12 | pico | p/p |
| 10-9 | nano | n/n |
| 10-6 | micro | μ/μ |
| 10-3 | Milli | m/m |
| 10-2 | centi | c |
| 10-1 | deci | d/d |
| 101 | soundboard | yes/da |
| 102 | hecto | g/h |
| 103 | kilo | k/k |
| 106 | mega | M |
| 109 | giga | G/G |
| 1012 | tera | T |
| 1015 | peta | P/P |
| 1018 | exa | E/E |
| 1021 | zeta | Z/Z |
| 1024 | yotta | Y/Y |
| 1027 | Ronna | R |
| 1030 | quecca | Q |
A current strength of 1A is a value equal to the ratio of a charge of 1 C passed through a surface (conductor) in 1 s of time to the time the charge passes through the surface. For current to flow, the circuit must be closed.
Current strength is measured in amperes. 1A=1Kl/1c
In practice there are
1kA = 1000A
1mA = 0.001A
1uA = 0.000001A
Electric voltage is the potential difference between two points in an electric field. The magnitude of electrical potential is measured in volts, therefore voltage is measured in volts (V).
1 Volt is the voltage that is necessary to release 1 Watt of energy in a conductor when a current of 1 Ampere flows through it.
1V=1W/1A.
In practice there are
1kV = 1000V
1mV = 0.001V
Electrical resistance is the characteristic of a conductor that prevents electric current from flowing through it. It is defined as the ratio of the voltage at the ends of the conductor to the current in it. Measured in ohms (ohms). Within certain limits the value is constant.
1 Ohm is the resistance of a conductor when a direct current of 1A flows through it and a voltage of 1V arises at the ends.
From the school physics course we all remember the formula for a homogeneous conductor of constant cross-section:
R=ρlS – the resistance of such a conductor depends on the cross-section S and length l
where ρ is the resistivity of the conductor material, tabular value.
Between the three quantities described above, Ohm's law exists for a DC circuit.
The current in the circuit is directly proportional to the voltage in the circuit and inversely proportional to the resistance of the circuit - Ohm's law.
I=U/R
Electrical capacitance is the ability of a conductor to accumulate electrical charge.
Capacitance is measured in farads (1F).
1F = 1Kl/1V
1F is the capacitance of a capacitor between the plates of which a voltage of 1V occurs when charged at 1C.
In practice there are
1pF = 0.000000000001F
1nF = 0.000000001F
Inductance is a quantity that characterizes the ability of a circuit through which electric current flows to create and accumulate a magnetic field.
Inductance is measured in henries.
1Gn = (V*s)/A
1H is a value equal to the self-inductive emf that occurs when the current in the circuit changes by 1A within 1 second.
In practice there are
1mH = 0.001H
Calculation formula
In 1841, the English scientist James Joule formulated a law for finding a quantitative measure of the thermal effect of electric current. In 1842, the same law was also discovered by the Russian physicist Emilius Lenz. Because of this, it received the double name of the Joule-Lenz law. In general, the law is written as follows: Q = I² • R • t.
It is quite general in nature, since it does not depend on the natural forces that generate the current. Today this law is actively applied in everyday life. For example, to determine the degree of heating of the tungsten filament used in light bulbs.
Joule-Lenz law
The Joule-Lenz law determines the amount of heat generated by a current. But, nevertheless, this will help to find out what formulas are used to calculate the work of the electric field. This is because it subsequently manifests itself in the form of heating of the conductor. This suggests that the work done by the current is equal to the heat of heating of the conductor (A=Q). Work of electric current, formula: A= I² • R • t. This is not the only formula for finding a job. If you use Ohm's law for a section of the chain (I=U:R), then you can derive two more formulas: A=I•U•t or A=U²:R.
You may be interested in this Features of the capacitor
Portraits of Joule and Lenz
The general formula for calculating power is that it is directly proportional to work and inversely dependent on time (P=A:t). If we talk about power in an electric field, then based on the previous formulas, we can create as many as three: P = I² • R; P=I•U; Р=U²:R.
Ohm's law for a circuit section
Interpretation of the law of conservation of energy. Joule-Lenz law
Ohm's law for a homogeneous section of a circuit with resistance R is reflected by the formula:
RI=U
Let's multiply both sides of the expression by IΔt and get the relation:
RI2∆t=UI∆t=∆A.
The result obtained is an expression of the law of conservation of energy for a homogeneous section of the chain.
Definition 2
The work ΔA of electric current I flowing through a stationary conductor with resistance R is converted into heat ΔQ released on the conductor.
∆Q=∆A=RI2∆t
This law is called the Joule-Lenz law.
The law bears the name of two famous physicists at once, since it was established experimentally by both of them independently of each other.
Definition 3
The power of the electric current is the ratio of the current work ΔA to the time interval Δt during which this work was performed.
It can be said more simply: power is work done per unit of time. Let us write down the formula connecting the work of the current and its power:
P=∆A∆t=UI=I2R=U2R
The work of an electric current is expressed in joules (J), the current power is measured in watts (W), time is measured in seconds (s): 1 W = 1 J1 s. The current power is measured using a wattmeter, and the work is calculated as a result of multiplying the current strength, voltage and time of current flow through the circuit: A=IUt.
Next, we will analyze a complete direct current circuit, including a source with an electromotive force δ and internal resistance r and an external homogeneous section with resistance R.
Definition 4
Ohm's law for a complete circuit looks like this:
(R+r)I=δ
Do you need help from a teacher? Describe the task - and our experts will help you! Describe the task
Let's multiply both sides of the expression with Δq=IΔt and get a relationship that will serve as an expression of the law of conservation of energy for a complete DC circuit:
RI2∆t+rI2∆t=δI∆t=∆Ast
The left side of the expression contains ΔQ=RI2Δt (heat that is released on the external section of the circuit during the time Δt) and ΔQist=rI2Δt (the heat that is released inside the source during the same time).
The expression δIΔt is equal to the work of external forces ΔAst that act inside the source.
Definition 5
When electric current flows through a closed circuit, the work of external forces ΔAst is converted into heat, which is released in the external circuit (ΔQ) and inside the source (ΔQist).
∆Q+Qist=∆Ast=δI∆t
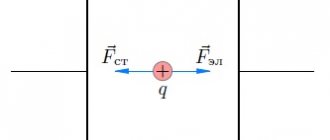
The following fact should be noted: the work of the electric field is not included in the indicated ratio. When current passes through a closed circuit, the electric field does no work; This means that heat is produced only through external forces that act inside the source. The electric field here redistributes heat between different sections of the circuit.
The external circuit can be not only a conductor with resistance R, but also some device that consumes power, for example, a DC motor. Then R must be regarded as the equivalent load resistance. The energy that is released in the external circuit has the ability to be partially or completely converted into both heat and other types of energy, for example, into mechanical work performed by an electric motor. Thus, the topic of using the energy of a current source is of great practical importance.
It will be interesting➡ Galvanometer - what it measures and how it works. The principle of operation of a galvanometer
Current measuring instruments
Electrical measuring instruments are a special type of devices that are used to measure many electrical quantities. These include:
- AC ammeter;
- AC voltmeter;
- Ohmmeter;
- Multimeter;
- Frequency meter;
- Electric meters.
Ammeter
To determine the current strength in an electrical circuit, you need to use an ammeter. This device is connected to the circuit in series and, due to its negligible internal resistance, does not affect its state. The ammeter scale is graduated in amperes.
In a classic device, a measured current passes through an electromagnetic coil, which creates a magnetic field that causes the magnetic needle to deflect. The deflection angle is directly proportional to the measured current.
Classic ammeter
An electrodynamic ammeter has a more complex operating principle. It contains two coils: one is movable, the other stands still. They can be connected to each other in series or in parallel. When current passes through the coils, their magnetic fields begin to interact, which as a result causes the moving coil with an arrow attached to it to deviate by a certain angle proportional to the magnitude of the current being measured.
Voltmeter
A voltmeter is used to determine the voltage (potential difference) across a section of the circuit. The device must be connected parallel to the circuit and have high internal resistance. Then only hundredths of the current will enter the device.
School voltmeter
The principle of operation is that inside the voltmeter there is a coil and a series-connected resistor with a resistance of at least 1 kOhm, on which the volt scale is calibrated. The most interesting thing is that the resistor actually registers the current strength. However, the divisions are selected in such a way that the readings correspond to the voltage value.
Ohmmeter
This device is used to determine electrically active resistance. The principle of operation is to change the measured resistance into a voltage directly dependent on it thanks to an operational amplifier. The desired object must be connected to a feedback circuit or to an amplifier.
You might be interested in the principle of operation and design of a magnetically controlled reed switch
If the ohmmeter is electronic, then it will work on the principle of measuring the current flowing through the required resistance at a constant potential difference. All elements are connected in series. In this case, the current strength will have the following dependence: I = U/(r0 + rx), where U is the emf of the source, r0 is the resistance of the ammeter, rx is the desired resistance. According to this dependence, resistance is determined.
Electronic ohmmeter
Multimeter
The devices given as an example are used today only in schools for physics lessons. Multimeters were invented for professional tasks. The most common device includes simultaneously the functions of an ammeter, voltmeter and ohmmeter. The device can be either easily portable or huge stationary with a large number of possibilities. The name “multimeter” was first applied specifically to a digital meter. Analog devices are more often called “avometer”, “tester” or simply “Tseshka”.
Universal multimeter
The work of current is a complex but very important topic in electrodynamics. Without knowing it, you will not be able to solve even the simplest problems. Even electricians use job finding formulas to make the necessary calculations.
What is electrical energy?
In this section we will take a closer look at electrical energy.
Charge distributions
Imagine an empty room, bringing electric charges to it one after another. As a result, you have a set of charge carriers. The work you had to do is now, to some extent, contained in this set. What kind of energy this is does not matter here. Much more important is the fact that this accumulation leaves an electric potential U(r) at every point in space.
What does this electrical potential do? If now you want to transfer another charge with an amount of charge q to point r, you must do the work Wel: Wel = q * U (r) .
If we also assume that the electric potential at the location of the container is zero, then this electric charge q contains the work Wel that you have done in the form of potential energy. And it is this potential energy that is called electrical energy.
Gravity analogy
Let's dig a little deeper into the gravity analogy. To calculate the potential energy when you are at a height h above the ground, you use the formula: Epot, g = m * g * h . In this formula, m stands for mass and g stands for gravitational acceleration. To make the analogy with electrical energy more obvious, let's combine the product g * h with the notation Ug, i.e. Ug = g * h.
Thus, the potential energy is equal to: Epot, g = m * Ug.
Let's take a quick look at the Ug unit. The unit of potential energy is the joule and the unit of mass is the kilogram. Thus, [Ug] = J/kg applies.
You will get the formula for electrical energy if you now replace m with electric charge q, and Ug with electric potential U: Epot, el = q * U.
Let us also consider the unit of U here. Electrical energy has the unit of joule and q has the unit of coulomb. Thus, [U] = J/C.
Rice. 1. Analogy between electricity and gravity
Now do you understand the analogy between “electrical fall” and gravity? If not, then perhaps the following table will help you:
| Type | Potential energy | Unit of measurement of "Potential" |
| Gravity | Epot, g = m * Ug | [Ug] = J/kg |
| Electricity | Epot, el = q * U | [U] = J/C |
However, electricity has a feature that has no analogy with gravity: "mass" can only be positive, but electric charge can be positive or negative. The smartphone always accelerates towards the ground because the gravitational potential there is lower than at altitude h. Positive electrical charges behave in a similar way: they accelerate from a location of high electrical potential to a location of lower electrical potential.
So, unlike "mass" and positive electrical charges, negative charges move towards a higher electrical potential.
Batteries
Imagine a simple electrical circuit: a battery connected to a light bulb. Once the electrical circuit is completed, the electrical energy contained in the negative charges at the negative terminal is converted into kinetic energy—the negative charges accelerate. As they pass through the light bulb, they collide with the atoms of the filament. In this case, the negative charges give up part of their kinetic energy to the atoms of the thread. They are then vibrated, causing the filament to heat up. This heating results in the emission of light. And it is this light that your eye perceives as the glow of a light bulb.
Note: energy conversion battery-lamp-circuit:
Electrical energy of negative charges -> kinetic energy of negative charges -> kinetic energy of atoms in the filament -> emission of light.
Rice. 2. Example of a simple circuit with a battery
Power determination problem
Condition. It is necessary to determine what the work and power of the electric current in the electric motor winding are equal to. It is known that the current strength in it is 90 A at a voltage of 450 V. The electric motor remains turned on for one hour.
Solution. First you can count the value of the work. For this, the following formula is useful: A = U * I * t. The first two quantities are given in SI units, but the time again needs to be converted to seconds, that is, take 3600 s.
After substituting the values and performing simple arithmetic operations, the following value for work is obtained: 145800000 J. It is more convenient to write it in the answer in larger units. For example, megajoules. To do this, the result must be divided by a million. The work turns out to be 145.8 MJ.
Now you need to calculate the power of the electric motor. Calculations will be performed according to the formula: P = U * I. After multiplication, the number obtained is: 40500 W. To write it in kilowatts, you need to divide the result by a thousand.
Answer. A = 145.8 MJ, P = 40.5 kW.
Voltage calculation problem
Condition. The electric stove has been plugged in for 20 minutes. What is the voltage in the network if, at a current of 4 A, the work is equal to 480 kJ?
Solution. Since the work and current strength are known, you need to use the following formula: A = U * I * t. Here voltage is an unknown factor. It must be calculated as the quotient of the product and a known factor, that is: U = A /( I * t).
Before making calculations, you need to convert the values to SI units. Namely, work in Joules and time in seconds. This will be 480,000 J and 1200 s. Now all that remains is to count everything.
Answer. The voltage is 100 V.
Job definition task
Condition. The resistance of a flashlight bulb is 14 ohms. The voltage supplied by the battery is 3.5 V. What will be the work done by the current if the flashlight worked for 2 minutes?
Solution. Since the voltage, resistance and time are known, it is necessary to use the following formula: A = (U2 * t)/R. Just first you need to convert the time into SI units, that is, seconds. Thus, you need to substitute not 2 minutes, but 120 seconds into the formula.
Simple calculations lead to the following value for the current work: 105 J.
Answer. The work is 105 J.