OGE 2022 in physics ›
1. Electric current, passing through a circuit, produces different effects: thermal, mechanical, chemical, magnetic. In this case, the electric field does work, and electrical energy is converted into other types of energy: internal, mechanical, magnetic field energy, etc.
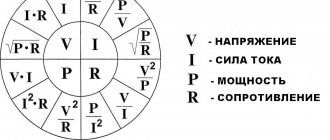
As has been shown, the voltage \( (U) \) in a section of the circuit is equal to the ratio of the work \( (F) \) performed when moving an electric charge \( (q) \) in this section to the charge : \( U=A/q \). Hence \( A=qU \). Since the charge is equal to the product of current \( (I) \) and time \( (t) \) \( q=It \), then \( A=IUt \), i.e. . The work done by an electric current on a section of a circuit is equal to the product of the voltage on that section, the current strength and the time during which the work is performed.
The unit of work is the joule (1 J) . This unit can be expressed in terms of electrical units:
\( [A] \)= 1 J = 1 V · 1 A · 1 s
To measure work, three measuring instruments are used: ammeter, voltmeter and clock, however, in real life, electric energy meters are used to measure the work of electric current.
If you need to find the work done by a current, but the current strength or voltage is unknown, then you can use Ohm’s law, express the unknown quantities and calculate the work using the formulas: \( A=\frac{U^2}{R}t \) or \( A=I^2Rt \).
2. The power of the electric current is equal to the ratio of the work to the time during which it was completed: \( P=A/t \) or \( P=IUt/t \); \( P=IU \) , i.e. The power of the electric current is equal to the product of voltage and current in the circuit .
The unit of power is the watt (1 W): \( [P]=[I]\cdot[U] \); \( [P] \) = 1 A · 1 V = 1 W.
Using Ohm's law, you can obtain other formulas for calculating current power: \( P=\frac{U^2}{R};P=I^2R \).
The power of the electric current in a conductor can be determined using an ammeter and a voltmeter by measuring the current and voltage, respectively. To measure power, you can use a special device called a wattmeter, which combines an ammeter and a voltmeter.
3. When electric current passes through a conductor, it heats up. This happens because free electrons in metals and ions in electrolyte solutions moving under the influence of an electric field collide with molecules or atoms of conductors and transfer their energy to them. Thus, when work is done by the current, the internal energy of the conductor increases, a certain amount of heat is released in it, equal to the work done by the current, and the conductor heats up: \( Q=A \) or \( Q=IUt \). Considering that \( U=IR \), \( Q=I^2Rt \).
The amount of heat released when current passes through a conductor is equal to the product of the square of the current strength, the resistance of the conductor and time.
This law is called the Joule-Lenz law.
EXAMPLES OF TASKS
Part 1
1. The current strength in the conductor was increased by 2 times. How will the amount of heat released in it per unit time change if the resistance of the conductor remains constant?
1) will increase by 4 times 2) will decrease by 2 times 3) will increase by 2 times 4) will decrease by 4 times
2. The length of the electric stove spiral was reduced by 2 times. How will the amount of heat released in the spiral per unit time change at a constant network voltage?
1) will increase by 4 times 2) will decrease by 2 times 3) will increase by 2 times 4) will decrease by 4 times
3. The resistance of the resistor \( R_1 \) is four times less than the resistance of the resistor \( R_2 \). Current work in resistor 2
1) 4 times more than in resistor 1 2) 16 times more than in resistor 1 3) 4 times less than in resistor 1 4) 16 times less than in resistor 1
4. The resistance of the resistor \( R_1 \) is 3 times greater than the resistance of the resistor \( R_2 \). The amount of heat that will be released in resistor 1
1) 3 times more than in resistor 2 2) 9 times more than in resistor 2 3) 3 times less than in resistor 2 4) 9 times less than in resistor 2
5. The circuit is assembled from a current source, a light bulb and a thin iron wire connected in series. The light bulb will glow brighter if
1) replace the wire with a thinner iron one 2) reduce the length of the wire 3) swap the wire and the light bulb 4) replace the iron wire with nichrome
6. The figure shows a bar graph. It shows the voltage values at the ends of two conductors (1) and (2) of the same resistance. Compare the values of current work \( A_1 \) and \( A_2 \) in these conductors for the same time.
1) \( A_1=A_2 \) 2) \( A_1=3A_2 \) 3) \( 9A_1=A_2 \) 4) \( 3A_1=A_2 \)
7. The figure shows a bar graph. It shows the current values in two conductors (1) and (2) of the same resistance. Compare the values of current work \( A_1 \) and \( A_2 \) in these conductors for the same time.
1) \( A_1=A_2 \) 2) \( A_1=3A_2 \) 3) \( 9A_1=A_2 \) 4) \( 3A_1=A_2 \)
8. If you use lamps with a power of 60 and 100 W in a chandelier to illuminate the room, then
A. A large current will be in a 100 W lamp. B. A 60 W lamp has greater resistance.
The following statement(s) are true:
1) only A 2) only B 3) both A and B 4) neither A nor B
9. An electric stove connected to a direct current source consumes 108 kJ of energy in 120 s. What is the current strength in the tile spiral if its resistance is 25 Ohms?
1) 36 A 2) 6 A 3) 2.16 A 4) 1.5 A
10. An electric stove with a current of 5 A consumes 1000 kJ of energy. What is the time it takes for the current to pass through the spiral of the tile if its resistance is 20 Ohms?
1) 10000 s 2) 2000 s 3) 10 s 4) 2 s
11. The nickeline spiral of the electric stove was replaced with a nichrome one of the same length and cross-sectional area. Establish a correspondence between physical quantities and their possible changes when the tile is connected to the electrical network. Write down the selected numbers in the table under the corresponding letters. The numbers in the answer may be repeated.
PHYSICAL QUANTITY A) electrical resistance of the spiral B) electric current strength in the spiral B) electric current power consumed by the tile
NATURE OF CHANGE 1) increased 2) decreased 3) did not change
12. Establish a correspondence between physical quantities and the formulas by which these quantities are determined. Write down the selected numbers in the table under the corresponding letters.
PHYSICAL QUANTITIES A) current work B) current strength C) current power
FORMULAS 1) \( \frac{q}{t} \) 2) \( qU \) 3) \( \frac{RS}{L} \) 4) \( UI \) 5) \( \frac{U}{I} \)
Part 2
13. The heater is connected in series with a rheostat with a resistance of 7.5 Ohms in a network with a voltage of 220 V. What is the resistance of the heater if the power of the electric current in the rheostat is 480 W?
AC operation and power
The energy supplied by the source of electromotive force to the external circuit undergoes transformation into other types of energy. If there is only active resistance in the circuit, then all the energy is converted into heat generated at the resistance. There is no phase shift between current and voltage. In addition, for a short period of time, alternating current can be considered as direct current. Therefore, the instantaneous power developed by alternating current across the resistance is:
| . |
Although current and voltage can be both positive and negative, power equal to their product is always positive. However, it pulsates, varying from zero to maximum value at a frequency equal to twice the AC frequency. In Fig. Figure 7.12 shows the time dependence of current, voltage and alternating current power released across the active resistance. It is clear that the average transmitted power is less than the maximum and equal to half the maximum power. The average value and for the period is . This can be explained as follows: , and for a full cycle the average value is equal to the average value . Therefore, the average power value will be equal to
| . |
Power factor is a dimensionless physical quantity that characterizes a consumer of alternating electric current from the point of view of the presence of a reactive component in the load. Power factor shows how much the alternating current flowing through a load is out of phase relative to the voltage applied to it.
Numerically, the power factor is equal to the cosine of this phase shift.
As you know, the energy consumed from an alternating current source consists of two components:
1. Active energy
2. Reactive energy
1. Active energy is that part of the consumed energy that is completely and irrevocably converted by the receiver into other types of energy.
Example: Flowing through a resistor, current does active work, which is expressed in an increase in the thermal energy of the resistor. Regardless of the phase of the flowing current, the resistor converts its energy into heat. The resistor does not care in which direction the current flows through it, only its magnitude is important: the larger it is, the more heat will be released on the resistor (the amount of heat released is equal to the product of the square of the current and the resistance of the resistor).
Reactive energy is that part of the consumed energy that in the next quarter of the period will be completely given back to the source.
VOLTAGE RESONANCE
It is known that in a mechanical system, resonance occurs when the natural frequency of oscillations of the system is equal to the oscillation frequency of the disturbing force acting on the system. Oscillations of a mechanical system, for example oscillations of a pendulum, are accompanied by a periodic transition of kinetic energy into potential energy and vice versa. When a mechanical system is at resonance, small disturbing forces can cause large oscillations of the system, for example, a large amplitude of oscillation of a pendulum.
In AC circuits where there is inductance and capacitance, resonance phenomena can occur, which are similar to the phenomenon of resonance in a mechanical system. A complete analogy - the equality of the natural frequency of oscillations of an electrical circuit to the frequency of the disturbing force (frequency of the network voltage) - is not possible in all cases.
In general, the resonance of an electrical circuit is understood as a state of the circuit when the current and voltage are in phase, and, therefore, the equivalent circuit of the circuit occurs at a certain ratio of its parameters r, L, C, when the resonant frequency of the circuit is equal to the frequency of the voltage applied to it .
Resonance in an electrical circuit is accompanied by a periodic transition of the energy of the electric field of the capacitor into the energy of the magnetic field and vice versa.
When there is resonance in an electrical circuit, small voltages applied to the circuit can cause significant currents and voltages in certain areas. In a circuit where r, L, C are connected in series, voltage resonance may occur, and in a circuit where r, L, C are connected in parallel, current resonance may occur .
Resonance is the phenomenon of a sharp increase in the amplitude of forced oscillations, which occurs when the frequency of natural oscillations coincides with the oscillation frequency of the driving force; the resonant frequency can be found from the expression
,
Where ; f is the resonant frequency in hertz; L is inductance in henry; C is the capacitance in farads.
Current work
Electric current, of course, would not have been used so widely if not for one circumstance. The work of current or electricity can be easily converted into any energy or work we need: thermal, mechanical, magnetic...
For the practical use of current, first of all, you want to know what kind of work can be turned to your advantage. Let us derive a formula for determining the work of the current:
Since all quantities included in the formula can be measured with appropriate instruments (ammeter, voltmeter, clock), the formula is universal.
The formula can also be written in a slightly different form using Ohm’s law:
If we substitute the current strength written in this way into the original formula for the work of current, we get:
If we express voltage from Ohm’s law, then:
The use of these formulas is convenient when there is one connection in the circuit: parallel for the first case and serial for the second
Answers
Oersted's experience. Magnetic field of current. Interaction of magnets. The effect of a magnetic field on a current-carrying conductor →
← Series and parallel connections of conductors
Work and power of electric current. Joule-Lenz law
3.1 (62.69%) 119 votes
What is power Watt [W]
Power is a quantity that determines the ratio of work performed by a current source over a certain period of time. One watt corresponds to the product of one ampere and one volt, but when determining energy costs, the value of kilowatt/hour .
It corresponds to the consumption of one thousand watts for 60 minutes of operation. It is by this indicator that the cost of electricity services is determined.
In most cases, the power consumed by the device is indicated in the technical documentation or on the packaging. The specified quantity is produced in one hour of work.
For example, a computer with a 500 W power supply will spin 1 kW for 2 hours of operation.
To help determine the current strength at a known power, a calculator will help, which converts one physical quantity to another.
Work in various conditions
The module of the complex indicator of movement intensity is equal to the full load indicator. The real component is equated to the active force, and the imaginary component is considered the reactive type. There is a positive or negative sign, which depends on the intensity of the circuit load. The complex power must match the associated electrical resistance. A positive load is characterized by the ratio P > 0, and the minus sign appears in the case of P < 0.
Measurement of the power characteristics of an alternating electron flow is carried out by passing a current of equal value through the phase conductors. Indicators of the flow force of charged particles using a neutral conductor have an insignificant dimension. Uniform or symmetrical phase load in a three-phase main depends on the magnitude of the flowing currents. Uneven or asymmetrical load depends on the flow through neutral or neutral cables. The overall power level is found by summing.
If there is a phase shift between voltage and current, then it coincides with the displacement angle between the vector radii of the electric current indicators. Under alternating voltage conditions, the coincidence of the vector radii of current and voltage is observed only in the absence of capacitors and induction coils in the circuit. The installation of inductors does not interfere with the coincidence of phase values. In this case, a vector rotation of equal intensity occurs. The internal angle displacement graph remains constant.
If a shift in voltage and alternating current occurs in the main line, then the power indicators are represented by a value with a negative sign , since the calculator multiplies positive and negative values. The duration of the periods depends on the level of phase displacement. In this case, the duration of negative loads determines the shear characteristics. In the calculations, resistance indicators are used, which are familiar from Ohm’s physical law.
Conversion rate factor
Power factor is a measure of current consumption in the presence of a reactive component and a distorting load. The meaning of the coefficient differs from the concept of the cosine of the shifted angle. The second concept is characterized by the displacement of the flowing alternating current, voltage, and is used only with a sinusoidal current and force of equal value.
The coefficient is equal to the ratio of the consumed load to its total value. In this case, the work is performed due to the active type of transformation. With sinusoidal current and voltage, the total load is the sum of the reactive and active forms. The active load is equal to the average product of current and voltage and cannot be higher than the product of similar root-mean-square dimensions. The power coefficient is shown in the range from 0 to 1 or set as a percentage from 0 to 100.
In a mathematical calculation, the numerical factor is interpreted as the cosine of the angle between the current vectors and the direction of voltage application. Therefore, with sinusoidal characteristics, the dimension of the coefficient can coincide with the cosine of the angle. If only sinusoidal voltage is used, and non-sinusoidal current is used with a load without a reactive component, then the numerical adapter is equal to the part of the load at the first distortion of the consumer current.
If a reactive element is present in the load, then, in addition to the power coefficient, the nature of the operation (capacitive-active or inductive-active) is indicated. The coefficient in these cases is different and is a lagging or leading value.
Power supply connections
When connecting N current sources with ℰ
1,
ℰ
2, …,
ℰ
N and resistances
r
1,
r
2, …,
r
N:
in series ℰ
= ±
ℰ
1 ±
ℰ
2 ± … ±
ℰ
N,
r
=
r
1 +
r
2 + … +
r
N;
parallel
like poles, if
ℰ
1 =
ℰ
2 = … =
ℰ
N , then
ℰ
=
ℰ
1 , \(~\frac{1}{r} = \frac{1}{r_1} + \frac{1}{r_2} + \ldots + \frac{1}{r_N}\) .
The sign of the EMF is determined by the mnemonic rule
: when moving along a current through a source, the emf is taken with the last sign.