Work and power of electric current. Joule-Lenz law

OGE 2022 in physics ›

1. Electric current, passing through a circuit, produces different effects: thermal, mechanical, chemical, magnetic. In this case, the electric field does work, and electrical energy is converted into other types of energy: internal, mechanical, magnetic field energy, etc.

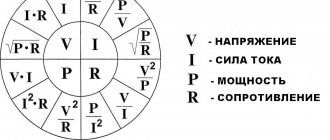
As has been shown, the voltage ​\( (U) \)​ in a section of the circuit is equal to the ratio of the work ​\( (F) \)​ performed when moving an electric charge ​\( (q) \)​ in this section to the charge : ​\( U=A/q ​​\)​. Hence ​\( A=qU \)​. Since the charge is equal to the product of current ​\( (I) \)​ and time ​\( (t) \)​ ​\( q=It \)​, then ​\( A=IUt \)​, i.e. . The work done by an electric current on a section of a circuit is equal to the product of the voltage on that section, the current strength and the time during which the work is performed.

The unit of work is the joule (1 J) . This unit can be expressed in terms of electrical units:

​\( [A] \)​= 1 J = 1 V · 1 A · 1 s

To measure work, three measuring instruments are used: ammeter, voltmeter and clock, however, in real life, electric energy meters are used to measure the work of electric current.

If you need to find the work done by a current, but the current strength or voltage is unknown, then you can use Ohm’s law, express the unknown quantities and calculate the work using the formulas: ​\( A=\frac{U^2}{R}t \)​ or ​\( A=I^2Rt \)​.

2. The power of the electric current is equal to the ratio of the work to the time during which it was completed: ​\( P=A/t \)​ or ​\( P=IUt/t \)​; ​\( P=IU \) ​, i.e. The power of the electric current is equal to the product of voltage and current in the circuit .

The unit of power is the watt (1 W): ​\( [P]=[I]\cdot[U] \)​; ​\( [P] \)​ = 1 A · 1 V = 1 W.

Using Ohm's law, you can obtain other formulas for calculating current power: ​\( P=\frac{U^2}{R};P=I^2R \)​.

The power of the electric current in a conductor can be determined using an ammeter and a voltmeter by measuring the current and voltage, respectively. To measure power, you can use a special device called a wattmeter, which combines an ammeter and a voltmeter.

3. When electric current passes through a conductor, it heats up. This happens because free electrons in metals and ions in electrolyte solutions moving under the influence of an electric field collide with molecules or atoms of conductors and transfer their energy to them. Thus, when work is done by the current, the internal energy of the conductor increases, a certain amount of heat is released in it, equal to the work done by the current, and the conductor heats up: ​\( Q=A \)​ or ​\( Q=IUt \)​. Considering that ​\( U=IR \)​, ​\( Q=I^2Rt \)​.

The amount of heat released when current passes through a conductor is equal to the product of the square of the current strength, the resistance of the conductor and time.

This law is called the Joule-Lenz law.

EXAMPLES OF TASKS

Part 1

1. The current strength in the conductor was increased by 2 times. How will the amount of heat released in it per unit time change if the resistance of the conductor remains constant?

1) will increase by 4 times 2) will decrease by 2 times 3) will increase by 2 times 4) will decrease by 4 times

2. The length of the electric stove spiral was reduced by 2 times. How will the amount of heat released in the spiral per unit time change at a constant network voltage?

1) will increase by 4 times 2) will decrease by 2 times 3) will increase by 2 times 4) will decrease by 4 times

3. The resistance of the resistor ​\( R_1 \)​ is four times less than the resistance of the resistor ​\( R_2 \)​. Current work in resistor 2

1) 4 times more than in resistor 1 2) 16 times more than in resistor 1 3) 4 times less than in resistor 1 4) 16 times less than in resistor 1

4. The resistance of the resistor ​\( R_1 \)​ is 3 times greater than the resistance of the resistor ​\( R_2 \)​. The amount of heat that will be released in resistor 1

1) 3 times more than in resistor 2 2) 9 times more than in resistor 2 3) 3 times less than in resistor 2 4) 9 times less than in resistor 2

5. The circuit is assembled from a current source, a light bulb and a thin iron wire connected in series. The light bulb will glow brighter if

1) replace the wire with a thinner iron one 2) reduce the length of the wire 3) swap the wire and the light bulb 4) replace the iron wire with nichrome

6. The figure shows a bar graph. It shows the voltage values ​​at the ends of two conductors (1) and (2) of the same resistance. Compare the values ​​of current work ​\( A_1 \)​ and ​\( A_2 \)​ in these conductors for the same time.

1) ​\( A_1=A_2 \)​ 2) \( A_1=3A_2 \) 3) \( 9A_1=A_2 \) 4) \( 3A_1=A_2 \)

7. The figure shows a bar graph. It shows the current values ​​in two conductors (1) and (2) of the same resistance. Compare the values ​​of current work \( A_1 \)​ and ​\( A_2 \) in these conductors for the same time.

1) ​\( A_1=A_2 \)​ 2) \( A_1=3A_2 \) 3) \( 9A_1=A_2 \) 4) \( 3A_1=A_2 \)

8. If you use lamps with a power of 60 and 100 W in a chandelier to illuminate the room, then

A. A large current will be in a 100 W lamp. B. A 60 W lamp has greater resistance.

The following statement(s) are true:

1) only A 2) only B 3) both A and B 4) neither A nor B

9. An electric stove connected to a direct current source consumes 108 kJ of energy in 120 s. What is the current strength in the tile spiral if its resistance is 25 Ohms?

1) 36 A 2) 6 A 3) 2.16 A 4) 1.5 A

10. An electric stove with a current of 5 A consumes 1000 kJ of energy. What is the time it takes for the current to pass through the spiral of the tile if its resistance is 20 Ohms?

1) 10000 s 2) 2000 s 3) 10 s 4) 2 s

11. The nickeline spiral of the electric stove was replaced with a nichrome one of the same length and cross-sectional area. Establish a correspondence between physical quantities and their possible changes when the tile is connected to the electrical network. Write down the selected numbers in the table under the corresponding letters. The numbers in the answer may be repeated.

PHYSICAL QUANTITY A) electrical resistance of the spiral B) electric current strength in the spiral B) electric current power consumed by the tile

NATURE OF CHANGE 1) increased 2) decreased 3) did not change

12. Establish a correspondence between physical quantities and the formulas by which these quantities are determined. Write down the selected numbers in the table under the corresponding letters.

PHYSICAL QUANTITIES A) current work B) current strength C) current power

FORMULAS 1) ​\( \frac{q}{t} \)​ 2) ​\( qU \)​ 3) \( \frac{RS}{L} \)​ 4) ​\( UI \)​ 5) \( \frac{U}{I} \)​

Part 2

13. The heater is connected in series with a rheostat with a resistance of 7.5 Ohms in a network with a voltage of 220 V. What is the resistance of the heater if the power of the electric current in the rheostat is 480 W?

What formula is used to calculate the work done by electric current?

If you set a charge q in motion in some section of an electrical circuit under the influence of an electric voltage U, then you can calculate the electrical work A as the voltage U applied at the ends of this section of the circuit multiplied by the electric charge q that passed through it, then is: A = U * q .

Knowing that the electric charge passing through a section of the circuit can be determined by measuring the current strength and the time it passes: q = I * t. Then the electrical work A [J] can be defined as the voltage U [V], multiplied by the current I [A] and multiplied by the time t [s], that is: A = U * I * q .

The work of an electric current on a section of a circuit is equal to the product of the voltage at the ends of this section by the current strength and the time during which the work was performed.

Below in the article we will look at two practical examples that will show the application of these formulas. However, before that, we will briefly look at a few more important formulas.

Note

: You must remember the first two formulas. The following formulas are less important, but may be useful for you in solving certain problems.

Other formulas for determining the work of electric current.

Ohm's law for a section of a circuit relates voltage U and current I. This allows us to calculate electrical work A in another way.

So, according to Ohm's law, U = I * R or I = U / R, where R is the electrical resistance.

Then you can substitute these formulas into A = U * I * t. As a result, we will obtain other formulas for finding the work of electric current:

• A = I2 * R * t ;
• A = (U2 * t) / R .

Answers

Oersted's experience. Magnetic field of current. Interaction of magnets. The effect of a magnetic field on a current-carrying conductor →

← Series and parallel connections of conductors

Work and power of electric current. Joule-Lenz law

3.1 (62.69%) 119 votes

Current work

Let's consider a section of the circuit through which current flows. We denote the voltage on the section, the resistance of the section is equal (Fig. 1).

Rice. 1. Chain section

Over time, a charge passes through our area. The charge is moved by a stationary electric field, which does work:

(1)

Due to work (1), thermal energy can be released in the area under consideration or mechanical work can be performed; chemical reactions may also occur. In short, this work is aimed at increasing the energy of our section of the chain.

Work (1) is called current work

. The term is extremely unfortunate - after all, it is not the current that does the work, but the electric field. But, alas, nothing can be done about the ingrained terminology.

If the chain section is homogeneous

, i.e. does not contain a current source, then Ohm’s law is valid for this section: . Substituting this into formula (1), we get:

(2)

Now let’s substitute in (1) instead of the current its expression from Ohm’s law:

(3)

Let us emphasize once again: formula (1) was obtained from the most general considerations, it is basic and is suitable for any section of the chain; formulas (2) and (3) are obtained from the main formula with the additional use of Ohm’s law and therefore are suitable only for a homogeneous area.

What is electric current and voltage

Electric current is the ordered movement of charged particles (electric charge carriers). The carriers of electric current are electrons (in metals and gases), cations and anions (in electrolytes), and holes in electron-hole conductivity. This phenomenon is manifested by the creation of a magnetic field, a change in the chemical composition or heating of the conductors. The main characteristics of the current are:

• The current strength, determined by Ohm's law and measured in Amperes (A), is denoted in formulas by the letter I;
• power, according to the Joule-Lenz law, measured in watts (W), is denoted by the letter P;
• frequency, measured in hertz (Hz).

Electric current, as an energy carrier, is used to obtain mechanical energy using electric motors, to obtain thermal energy in heating devices, electric welding and heaters, to excite electromagnetic waves of various frequencies, to create a magnetic field in electromagnets and to obtain light energy in lighting devices and various types of lamps .

Voltage is the work done by an electric field to move a charge of 1 coulomb (C) from one point on a conductor to another. Based on this definition, it is still difficult to understand what tension is.

In order for charged particles to move from one pole to another, it is necessary to create a potential difference between these poles (this is what is called voltage). The unit of measurement for voltage is the volt (V).

For a final understanding of the definition of electric current and voltage, an interesting analogy can be given: imagine that the electric charge is water, then the pressure of the water in the column is the voltage, and the speed of water flow in the pipe is the strength of the electric current. The higher the voltage, the greater the electric current.

What is alternating current

If you change the polarity of the potentials, the direction of flow of electric current changes. It is this current that is called alternating. The number of changes in direction over a certain period of time is called frequency and is measured, as mentioned above, in hertz (Hz). For example, in a standard electrical network in our country, the frequency is 50 Hz, that is, the direction of current movement changes 50 times per second.

What is direct current

When the ordered movement of charged particles always has only one direction, then such a current is called constant. Direct current occurs in a constant voltage network when the polarity of charges on one side and the other is constant over time. It is very often used in various electronic devices and technology when energy transfer over long distances is not required.

It will be interesting➡ Electrolizsols, alkalis, acids

Work and current power. Joule-Lenz law

• Electric current is so widely used because it carries energy. This energy can be converted into any form.

Work done by current
During the ordered movement of charged particles in a conductor, the electric field does work. This work is usually called current work.

If during a period of time Δt a charge Δq passes through the cross section of an arbitrary section of a conductor, then the electric field will do work during this time (see § 1.19)

where U is the voltage at the ends of the conductor. Since the current strength

then this work is equal to:

The work done by the current in a section of the circuit is equal to the product of the current, the voltage in that section and the time during which the work was done.

According to the law of conservation of energy, this work must be equal to the change in the energy of the section of the circuit under consideration. Therefore, the energy released in a given section of the circuit during the time Δt is equal to the work of the current [see. formula (2.7.1)].

If in formula (2.7.1) we express either voltage in terms of current (U = IR) or current in terms of voltage (I = U/R), we obtain two more formulas for the work of current:

Formula (2.7.1) is universal, since to derive it we used only the law of conservation of energy, which is valid in all cases. Formulas (2.7.2) and (2.7.3) are obtained from formula (2.7.1) using Ohm’s law for homogeneous sections of the chain. Therefore, these formulas are valid only in the case when the work of the current is completely used to increase the internal energy of the conductor.

Formula (2.7.2) is convenient to use when connecting conductors in series, since the current strength in this case is the same in all conductors. Formula (2.7.3) is convenient when connecting conductors in parallel, since the voltage on all conductors is the same.

Current power

Any electrical device (lamp, electric motor, etc.) is designed to consume a certain amount of energy per unit of time. Therefore, along with the work of current, the concept of current power is very important. The current power P is equal to the ratio of the work done by the current A during the time Δt to this time interval:

Using formula (2.7.1), we can give equality (2.7.4) the form:

Formula (2.7.5) is a universal formula for calculating current power. Using Ohm's law, you can obtain two more formulas for current power:

Formulas (2.7.6) and (2.7.7), as well as (2.7.2) and (2.7.3), are suitable only when the work of the current is completely used to increase the internal energy.

The SI unit of work for current is the joule (J) and power is the watt (W). In practice, the off-system unit of current work is widely used - kilowatt-hour (kW • h): 1 kW • h = 3.6 • 10 6 J.

Joule-Lenz law

If no mechanical work is performed on a section of the circuit and the current does not produce chemical effects, then only heating of the conductor occurs. A heated conductor gives off heat to surrounding bodies.

Heating of a metal conductor occurs as follows. An electric field accelerates electrons. After colliding with ions of the crystal lattice, they transfer their energy to the ions. As a result, the energy of the chaotic movement of ions near equilibrium positions increases. This means an increase in internal energy. The temperature of the conductor rises, and it begins to transfer heat to surrounding bodies. A short time after the circuit is closed, the process is established and the temperature stops changing over time. Due to the work of the electric field, energy is continuously supplied to the conductor. But its internal energy remains unchanged, since the conductor transfers to surrounding bodies an amount of heat equal to the work done by the current. The latter is true only when the work of the electric current is completely spent on increasing internal energy. In this case, the amount of heat transferred by the current-carrying conductor to other bodies can be calculated using any of the formulas (2.7.1)—(2.7.3):

However, if in a given section of the circuit there is a transformation of energy into mechanical or chemical energy, then the amount of heat released by the conductor with current is less than the work done by the current*.

To calculate the amount of heat released in this case, only formula (2.7.2) is suitable:

This is the Joule-Lenz law, established experimentally in 1842 by the Russian academician E. H. Lenz and, independently of him, by the English physicist D. Joule.

The Joule-Lenz law is formulated as follows: the amount of heat released by a conductor carrying current is equal to the product of the square of the current strength, the resistance of the conductor and the time it takes for the current to pass.

The Joule-Lenz law (2.7.9) is valid not only for metal conductors, but also for solutions of electrolytes and gases. In these cases, the internal energy of a liquid and gaseous conductive substance also increases due to collisions of orderedly moving charged particles with other charged or neutral particles of the substance.

Determination of the work of electric current

Work as such is a quantity that describes the transition of energy into another form. For example, when an object moves, it has kinetic energy. After the movement stops and the object rises to a certain height, we can talk about the transition of energy into potential form.

When electric charges move in a circuit through a conductor material, their movement is initiated by an electric field, so we can say that the workload lies with the latter. Thus, the work of electric current is a quantity that characterizes the transformation of electricity into other types, for example, mechanical energy or heat. In formulaic representations, the quantity is denoted by the capital Latin letter A.

Important! The modulus of the work of an electric current is equal to the product of the period of time during which it was performed, the value of the current strength and the voltage at the ends of the electrical circuit fragment. When any of the components of the product increases or decreases, the work rate will change in the same direction. The value itself shows how much electrical energy has undergone transformation into its other types over a certain period of time.

Examples of Ohm's law calculations

Let's find the voltage if the current is 0.9 Amperes and the resistance is 100 Ohms, using a triangle, cover the voltage with your hand, look, the vertical line means multiply. We use that formula again, just substitute the numbers, U = 0.9 A * 100 Ohm, we think it turns out to be 90, which means U = 90 volts.

Now we calculate the resistance, take the same units, only remove the resistance, we get this formula: R = 90 V \ 0.9 A, we get 100 Ohms.

To calculate the current, we again remove the current, we get this formula I = 90 V \ 100 Ohm, we get 0.9 Amperes. So, that's all, by the way, Ohm's law applies where there are no inductors and capacitors, don't worry about capacitors and inductors, just remember that Ohm's law applies where there are no inductors and capacitors. I hope my article was useful, good luck to everyone, Dmitry Tsyvtsyn was with you.

§ 22. Work and power of electric current

The ability of a body to produce work is called the energy of that body

.
For example, a load raised to a height has a certain amount of energy and produces work when falling. Work is measured in joules ( J
).
The energy of a body is greater, the more work this body can produce during its movement. Energy does not disappear, but passes from one form to another. For example, electrical energy can be converted into mechanical, thermal, chemical, etc. To transfer charges in a closed circuit, a source of electrical energy expends a known energy equal to the product of e. d.s. source on the amount of electricity transferred through this circuit, i.e. A
0 =
E q
. However, not all energy is useful, that is, not all the work done by the energy source is communicated to the energy receiver, since part of it is spent on overcoming the internal resistance of the source and wires. Thus, the source of electrical energy produces useful work equal to

A

=
U q
,

where U

— voltage at the receiver terminals,
in
. At a constant current, the amount of electricity is equal to the product of the current in the circuit and the time it passes, i.e.

q

=
I t
,

then the work formula can be presented as follows:

A

=
UI t
, (28)

i.e. the work of electric current is equal to the product of voltage, current strength in the circuit and the time it passes

.

If we express the voltage at the terminals of a section of the circuit as the product of the current strength and the resistance of this section, i.e.

U

=
Ir
,

then the work formula can be written as follows:

A

=
I
2
r t
. (29)

However, none of the above formulas determines the size of the electrical energy generator from which this work is obtained, since both large and small generators can produce the same work, but at different time intervals. Therefore, the size of the generator is determined not by the work performed, but by its power. This applies to any electrical apparatus and machine (electric motors, electric lamps, heating devices, etc.). Power is the work done (or consumed) in one second.

. Power can be represented by the following formula:

If in the work and power formulas voltage is expressed in volts, current in amperes, resistance in ohms and time in seconds, then work is expressed in newton-meters or watt-seconds ( W sec

), i.e. in joules (
J
), and power - in watts (
W
).
To measure low powers, a unit is used that is a thousand times smaller than 1 W
, called a milliwatt (
mW
);
1 W
= 1000
mW
.
To measure high powers, a unit a thousand times larger than the watt is used, called the kilowatt ( kW
);
1 kW
=

1000
W. Since the watt-second (joule) is a small unit, work is usually expressed in larger units: watt-hours ( w h
) and kilowatt-hours (
kw h
).
The relationships between these units and the joule are as follows: 1 W h
= 3600
J
;
1 kW h

=
3,600,000
J. The power in the external circuit at voltage U
at the generator terminals is equal to the product of voltage and current, i.e.

P=UI

.

With very low external resistance, the current in the circuit is high, and the voltage at the generator terminals is small. If the resistance of the external circuit is zero, then the voltage at the generator terminals U

is also equal to zero, therefore the power
P
given to the external circuit is equal to zero.
With a very large external resistance (when the external circuit is open, its resistance is infinitely large), the current in the circuit is zero. The power supplied to the external circuit is also zero in this case. Thus, with an increase in the resistance of the external circuit, the power first increases from zero to some largest (maximum) value, and then decreases to zero. The external circuit resistance r
, at which the energy source delivers the greatest power to the receiver, is equal to the internal resistance of the source, i.e.
r
=
r
0. However, it must be borne in mind that if the internal resistance of the generator is equal to the resistance of the external circuit, the useful power of the generator is insufficient and its work in such conditions it is uneconomical, since half of the total power developed by the generator is spent on overcoming its internal resistance.

Example.

Energy source with e.
d.s. E
= 120
V
and internal resistance
r
0 = 10
ohms
is closed to the load, the resistance of which sequentially takes the following values:
r
= 30;
20; 10; 5 and 2 ohms
. Determine the power supplied by the energy source to the external circuit at various load resistances. Solution. The current strength in the closed circuit and the power in the external circuit are equal:

With load resistance r

= 30
ohm
at r

= 20
ohm
at r

= 10
ohm
at r

= 5
ohms
at r

= 2
ohm
From the considered example it is clear that the maximum power in the external circuit is 360 W

will be with a load resistance equal to the internal resistance of the energy source, i.e.
r
=
r
0 = 10
ohm
.
Previous page

Derived units of power and work

How is power measured?

The basic power measurement unit in the international SI system is the watt (W). One watt is the power when, within one second, the current does work equal to one joule. Using other units of measurement, watt can be expressed as follows:

• 1 W = 1 m2 * 1kg/1s3 (square meter, kilogram and cubic second, respectively);
• 1 W = 1 N * 1 m/s (newton and meter per second);
• 1 W = 1 J/1 s (joule and second) - follows directly from the given definition of the unit.

Also equivalent to a watt is the Russian non-system unit - volt-ampere (V*A).

Multiple derived power quantities are:

• hectowatt - it is equal to one hundred watts;
• kilowatt is equal to a thousand watts.

Such large units are used in the design of railway electric trains and the production of electrical energy. There are also small sub-multiple units, for example, microwatt (1 µW = 10-6 W), they are used in the manufacture of electrocardiographs and electroencephalographs. Even smaller units are picowatts and nanowatts, they are used in the electronics industry. One nanowatt (nW) is equal to 10-9 W, and one picowatt (pW) is 10-12 W.

Another non-system value is horsepower (hp), equal to 735.5 watts. In Russian industry it has officially fallen out of use, but in fact is still in use in those areas where internal combustion engines are used.

The relationship between joule and kilowatt-hour can be expressed in terms of intermediate units:

• A joule is equivalent to one watt-second;
• 60 watt-seconds equals 1 watt-minute, which in turn equals 60 joules;
• 60 watt-minutes equals 3600 joules or 1 watt-hour;
• one hundred watt-hours is equal to one hectowatt-hour (360,000 joules);
• One thousand watt-hours is one kilowatt-hour (3,600,000 joules).

A digital wattmeter is used to measure power

Units

Current density - what is it and how is it measured?

The basic unit used to express the transformation carried out by electric current is the joule. The unit received this name after the name of the English physicist who experimentally substantiated the law of conservation of energy. Joule is abbreviated as "J". You can express a value through other units of measurement using the basic formula: 1 J = 1 A*1V*1 s (ampere, volt and second, respectively).

Important! Meters for metering consumed electricity use a different unit of measurement - kilowatt-hour (indicated as kW*h). This is due to the fact that the joule is a very small unit, and one kilowatt-hour is equal to 3,600,000 joules. Since the operation of lighting fixtures and household appliances in a residential apartment or house lasts hundreds of hours every month, and in the process significant work of current is realized, the kilowatt-hour is a much more adequate measuring unit for the given conditions.