Action of an electric current source
In any electrical circuit, charge carriers move through the links of the chain. This movement is possible only under the influence of a certain electric field. Therefore, in any electrical circuit there must be a special element that will create an electric field that moves charges.
Such an element is called an electric current source. The current source has two contacts (poles), with the help of which the electric field is maintained. There is always some difference in electrical potential between the poles. Now, if an electric circuit is connected to these poles, then the charge carriers under the influence of the field will begin to move, performing useful work in the circuit. At the same time, a process must constantly occur in the current source that would maintain the potential difference at the poles, despite the movement of charge carriers along the circuit.
Rice. 1. Types of electric current sources.
Electromotive force. Ohm's law for a complete circuit
In previous lessons, we talked about the fact that for an electric current to arise, there must be free charged particles that can move along a conductor under the influence of electric field forces. We also learned that the movement of free charged particles in a conductor under the influence of electric field forces leads to the appearance of induced charges. These charges create an electric field inside the conductor, which completely compensates for the external electric field, so the movement of free charged particles in the conductor quickly stops.
To maintain a constant electric current in a conductor, it is necessary that the conductor be part of a closed circuit containing a current source in which work is carried out to move charges against the forces of the electric field. Current sources can be different in design, but in any of them
work is done to separate positively and negatively charged particles.
As a result of the separation of charges, they accumulate at the poles of the source and, as a result, a potential difference arises at the poles. The resulting electric field inside the current source counteracts the separation of charges. If the circuit is opened, then when a certain potential difference is reached at the poles of the source, the separation of charges stops. At the same time, the operation of the current source also stops. Connecting the poles of the current source with a conductor, which will represent the external section of the circuit
, we will create an electric field in it, which will act on the electrical charges of the conductor.
Electric charges in an external circuit (for example, electrons in a metal) will move, which will cause a current. Excess charges of the negative pole of the source will begin to flow into the external section of the circuit, while at the positive pole its positive charge will be neutralized. Thus, the excess charge on both poles of the current source will be reduced. This will lead to the fact that charge separation will begin to occur in the source again and it will continue as long as the circuit remains closed. In the external section of the circuit, work will be done by the forces of the electric field. Inside the current source, work will be done by forces of a non-electrostatic nature developed by the current source.
These forces are usually called
external forces.
The quantity measured by the ratio of the work done by external forces when moving a charge along a closed circuit to the absolute value of this charge is called the electromotive force of the current source
(abbreviated
EMF
).
It is denoted by the Greek letter ξ
, and is measured, like voltage,
in volts (V).
Despite the fact that the emf of the source when the circuit is open is equal to the potential difference across the source terminals,
the work of external forces cannot be expressed through a potential difference, since external forces are non-potential and their work depends on the shape of the trajectory of the charges.
You already know that any complete electric current circuit consists of two parts: external and internal. The external part of the circuit consists of various consumers and supply wires
.
The internal part of the circuit includes a current source with resistance (this resistance is usually called internal).
When a circuit is closed, an electric current exists in both the external and internal parts of the circuit. Since the current source also has resistance, the voltage drop occurs both in the external and in the internal part of the circuit.
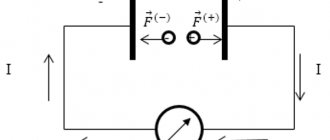
Let us include a resistance in the circuit of some current source and determine experimentally the sum of the voltage drops in the external and internal parts of the circuit. In the presented installation, an ammeter and a rheostat are included in the external circuit. The voltage drop in the external part of the circuit is measured by a voltmeter, which is connected to the terminals of the element, and a second voltmeter measures the voltage drop across the internal resistance of the element. A rheostat can change the current in a circuit; In this case, the readings of the voltmeters will change.
So, from the results of the experiment it is clear that the sum of the voltage drops in the external and internal parts of the circuit, within the experimental errors, is a constant value, on average equal to 1.02 V)
If you measure the voltage at the terminals of the element with the external circuit open, it will also be equal to 1.02 V. Thus, experience shows that the sum of the voltage drops in all sections of the closed circuit is equal to the voltage at the poles of the current source with the external circuit open.
But, as you and I already know, the voltage or potential difference at the poles of the current source when the external circuit is open is equal to the EMF of the current source. Consequently, the electromotive force of the current source is equal to the sum of the voltage drops in all sections of the closed electrical circuit.
Let us denote the resistance of the external part of the circuit as R
, and internal - through
r
.
Let the current in the circuit be equal to I
, and the emf of the source -
ξ
. Then, according to the definition of EMF (and based on the results of our experiments), we can write the following expression:
Expressing the current value from the written equality, we obtain the mathematical expression of Ohm’s law for the complete circuit
, which is formulated as follows:
the current strength in a complete electrical circuit is directly proportional to the emf of the current source and inversely proportional to the total resistance of the circuit:
But let's return to our previous formula. So, we know that in the case of a homogeneous section of the circuit, the product of the current strength and the resistance of this section is the voltage drop:
Then we can write that the voltage drop in the external section is equal to the difference between the EMF of the current source and the product of the current strength and the internal resistance of the source:
Now let’s substitute into this equation the expression for the current from Ohm’s law for the complete circuit:
Analysis of the formula we obtained allows us to draw two very important conclusions. Firstly, when
the circuit is open (when the external resistance tends to infinity), the voltage at the poles of the current source is equal to the emf of the current source: U
=
ξ
.
This is the basis for the possibility of approximately measuring the EMF of a current source using a voltmeter.
And secondly, if the resistance of the external section of the circuit tends to zero, then the current strength in the circuit increases and reaches its maximum value.
The voltage drop across the current source is equal to the EMF, and the voltage between its poles is zero.
This mode of operation of the current source is called a short circuit, and the maximum current strength for a given source is called the short circuit current:
The short circuit mode is extremely dangerous because it can damage the current source and even cause a fire.
To determine the sign of the EMF of any source, you must first agree on the choice of the positive direction of bypassing the circuit. Let us say right away that this choice is made absolutely arbitrarily.
.
After this, it is believed that if a given source causes a current in the bypass direction, then its EMF is considered positive. Otherwise - negative.
Moreover, if the electrical circuit contains several current sources, then the algebraic sum of the products of the current strengths and the resistance of the corresponding sections is equal to the algebraic sum of the emfs present in the circuit:
This statement is called Kirchhoff's second rule.
To consolidate the new material, we will solve the following problem. In a conductor with a resistance of 2 Ohms, connected to a current source with an emf equal to 1.1 V, the current strength is 0.5 A. Determine the strength of the short circuit current.
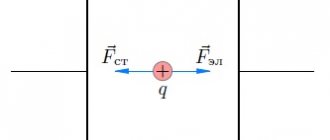
Outside forces
In order to maintain the potential difference at the poles of the current source, it is necessary to do work to transfer charges between the poles. Moreover, this transfer must be carried out against the action of the existing electric field. In fact, if the charge carrier has a negative charge (for example, a free electron), then, having arrived at the positive pole, it must be transferred inside the source to the negative pole, despite the fact that the field will still move it towards the positive.
This means that the transfer of charges within a source of electric current must be carried out by forces of a nature other than electrical. Therefore, these forces are called third-party.
The nature of external forces may vary. In batteries and accumulators, these are forces of a chemical nature. In industrial generators, the nature of external forces is mechanical. In solar batteries - light.
Rice. 2. Third-party forces of various natures.
Ohm's law for an arbitrary section of a circuit
The section of the chain on which external forces act is called heterogeneous. It satisfies the following equality:
$$U_{12}=\varphi_{1}-\varphi_{2}+\varepsilon_{12}(4)$$
where U12=IR21 – voltage drop (or voltage) in circuit section 1-2 (I-current); $\varphi_{1}-\varphi_{2}$ – potential difference between the ends of the section; $\varepsilon_12$ is the electromotive force contained in the circuit section. $\varepsilon_12$ is equal to the algebraic sum of the emf of all sources that are located in a given area.
It should be taken into account that EMF can be positive and negative. The EMF is called positive if it increases the potential in the direction of the current (the current flows from the minus to the plus of the source).
Electromotive force as a measure of external forces
So, the action of the current source is to, with the help of external forces, perform work on the transfer of electric charges between the poles against the action of the electric field. To characterize this work, there is a special measure called electromotive force (EMF, denoted by the letter $\mathscr{E}$). Its physical meaning is that it is the work of external forces to transfer a unit of charge. That is, the EMF is equal to the ratio of the work done by external forces to transfer charge against the action of the electric field to the magnitude of this charge:
$$\mathscr{E} = {A_{st}\over q}$$
From this formula you can obtain the unit of measurement of EMF. It is the same as voltage - Volt (remember, 1 V = 1 J / 1 C).
The EMF of a regular AA battery is 1.5V. That is, in it, external forces of a chemical nature perform 1.5 J of work to transfer 1 C of charge.
Rice. 3. AA batteries.
Difference Between Electromotive Force (EMF) and Voltage
The emf is generated by the source.
Voltage
It is simply the potential difference between two points in a circuit.
Electromotive force is different from the output voltage of a device when current flows. The voltage at the battery terminals, for example, is less than the emf when the battery is delivering current, and it decreases as the battery discharges. However, if the device's output voltage is measured without drawing current, the device's output voltage will be equal to the emf, even for a very discharged battery.