Dielectric constant of a substance
Some substances can weaken the interaction of charges.
Substances that weaken the interaction of charged particles are called insulating substances, or dielectrics.
For clarification, consider the electrical properties of distilled water.
Let us place two positive charges in a vacuum at a certain distance from one another, they will be repelled by Coulomb forces.
Then, without changing the charges and the distance between them, we move them into distilled water. We will find that in water they will repel each other 81 times less (Fig. 1).
Rice. 1. Two positive charges located at a distance r in distilled water repel each other 81 times less than in vacuum
In the lower part of the figure, the repulsive forces of charges in water are indicated by short blue vectors. The length of these vectors should be 81 times less than the length of the force vectors in vacuum at the top of the figure. However, the vectors are longer in the figure than in reality, since if they are reduced by the required number of times, they will not be visible.
Dielectric constant \(\large \varepsilon\) describes the insulating properties of dielectrics. It shows how many times the interaction of charges inside a substance - a dielectric - is weakened.
\[\large \boxed { \varepsilon = \frac{F_{\text{vacuum}}}{ F_{\text{substance}}} } \]
The weakening of the interaction occurs due to the weakening of the electrostatic field strength in the dielectric.
\[\large \boxed { \varepsilon = \frac{\overrightarrow{E_{\text{vacuum}}}}{\overrightarrow{E_{\text{substance}}}} } \]
Dielectric constant of some substances
You can use these tablets to solve most school physics problems.
Table 1. Diel. permeability of some solids
For some substances, permeability values are rounded. For example, there are glasses with a permeability value of 6.0, and at the same time, the permeability of some glasses can reach a value of 10.0. And the table for glass shows an average value of 8.0.
Table 2. Diel. permeability of some liquids
To carry out more serious calculations that are not related to educational calculations, please use specialized reference books.
Notes[edit | edit code]
- CODATA Value: electric constant. The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. Retrieved 2015-09-25. 2014 CODATA recommended values.
- Fedosin SG The Force Vacuum Field as an Alternative to the Ether and Quantum Vacuum. WSEAS Transactions on Applied and Theoretical Mechanics, ISSN/E-ISSN: 1991-8747/2224-3429, Volume 10, Art. #3, pp. 31-38 (2015); article in Russian: Force vacuum field as an alternative to ether and quantum vacuum.
- Fedosin SG The charged component of the vacuum field as the source of electric force in the modernized Le Sage's model. Journal of Fundamental and Applied Sciences, Vol. 8, No. 3, pp. 971-1020 (2016). https://dx.doi.org/10.4314/jfas.v8i3.18, https://dx.doi.org/10.5281/zenodo.845357. // Charged component of the vacuum field as a source of electric force in the modernized Le Sage model.
Expression through the parameters of the vacuum field[edit | edit code]
In the concept of a force vacuum field [2], it is assumed that the electrogravitational vacuum is filled with particle flows that create gravitational and electromagnetic forces between bodies. In particular, flows of charged particles—praons—moving at relativistic speeds and transferring their momentum to the charged matter are considered responsible for the occurrence of the Coulomb force between charges.
In the model of cubic distribution of praon fluxes for the electric constant, the following is obtained: [3] ε 0 = e 2 6 pq D 0 q ϑ 2 = e 2 ε cq ϑ 2 . ~ \varepsilon_0 = \frac {e^2}{6 p_q D_{0q} \vartheta^2 }= \frac { e^2} {\varepsilon_{cq}\vartheta^2 } .
Here pq ~ p_q is the momentum of praons interacting with charged matter; the fluence power D 0 q ~ D_{0q} denotes the number of praons dN that fell during the time dt onto the area dA perpendicular to the flow of one of the faces of a certain cube limiting the volume under consideration; ϑ = 2.67 ⋅ 10 − 30 ~ \vartheta = 2.67 \cdot 10^{-30} m² is the cross section for the interaction of praons with nucleons; e ~ e – elementary charge; ε cq = 4 ⋅ 10 32 ~ \varepsilon_{cq}= 4 \cdot 10^{32} J/m³ – energy density of praon fluxes for cubic distribution.
In the model of the spherical distribution of praon fluxes in space: ε 0 = e 2 16 π pq B 0 q ϑ 2 = 3 e 2 2 ε sq ϑ 2 , ~ \varepsilon_0 = \frac {e^2}{16\pi p_q B_{ 0q} \vartheta^2} = \frac { 3e^2}{2 \varepsilon_{sq} \vartheta^2},
where the fluence power B 0 q ~ B_{0q} denotes the number of praons dN that fell during the time dt from a unit solid angle d α d{\alpha} inside the spherical surface dA; ε sq = 6 ⋅ 10 32 ~ \varepsilon_{sq} = 6 \cdot 10^{32} J/m³ – energy density of praon fluxes for a spherical distribution.
It follows that the electric constant is a dynamic variable depending on the parameters of the particles of the vacuum field.
Direct electric current
Direct electric current is the directional, ordered movement of elementary (material) particles carrying electric charges. At the same time, negatively charged particles - electrons - move in metals (metallic conductors), as well as in a vacuum, and in liquids (solutions of salts and acids) - both negatively and positively charged material particles - ions moving in opposite directions (towards each other ). In rarefied gases, electric current can be carried out by the movement of both electrons and ions.
Direct current - does not change over time, i.e. is constant in direction and magnitude. The direction of direct current is taken to be the direction of movement of positively charged particles. It follows that in metal conductors, as well as in vacuum and gases, the direction of the current is taken opposite to the direction of movement of electrons.
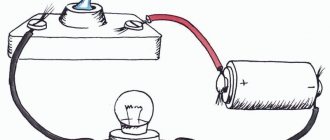
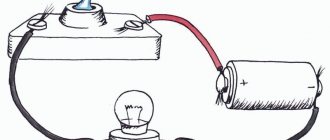
The simplest DC circuits. The simplest direct current circuit consists of the following elements: a source of electricity; electrical receiver (energy consumer); wires
In addition, the current circuit usually includes measuring instruments and certain devices for turning the current on and off.
The representation of an electrical circuit using conventional graphic symbols is called an electrical circuit (Fig. 1.1). Any source of electricity has an electromotive force (EMF), under the influence of which the movement of elementary particles carrying electrical charges occurs in it, and a potential difference is created at its poles. Electromotive force is denoted by the Latin letters E or e.
The difference in electrical potential between the poles of a current source, under the influence of which an electric current flows in an external circuit, is called the electrical voltage acting in this circuit. Voltage is denoted by the Latin letter U. The unit of measurement for EMF and voltage is volt (V). The instruments for measuring them are called voltmeters.
The strength of electric current is designated by the letter / and is measured in amperes (A). A device for measuring current is called an ammeter.
Electric current can only flow through a circuit when it is closed, i.e. when a continuous path is provided for electrical charges from the “plus” of the current source to the “minus” (see Fig. 1.1). Therefore, in this case, in order for current to appear in the circuit, it is necessary to close switch 5. The presence of current in the circuit will be detected by the lighting of the electric lamp 4 and the reading of ammeter 3. The voltage value in the circuit is determined by the reading of voltmeter 2. If you open switch 5 and thereby break electrical circuit, the current in it will stop, the lamp will go out, and the ammeter needle will go to zero.
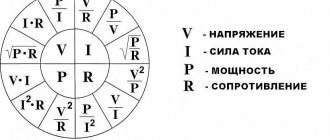
DC operation and power. The power of a direct electric current is determined by the product of the voltage U acting in the circuit and the current I flowing through the circuit. The unit of power is watt (W).
Power is designated by the letter P and is determined by the formula
P =UI. (1.1)
When measuring voltage in volts and current in amperes, the power value is expressed in watts.
The work of electric current (A), equal to the amount of electrical energy expended during a given time, is determined by the formula
A= Pt= UIt (1.2)
where P is the power of direct electric current, W; t is the time during which this power was given, s; U is the voltage acting in the circuit, V; I - current strength, A.
The work of electric current, determined by formula (1.2), is expressed in joules (J) or kilowatt-hours (kW h). It is easy to calculate that 1 kWh is equal to 3,600,000 J.
Application[edit | edit code]
The electric constant appears in Maxwell's vacuum equations, which describe the properties of electric and magnetic fields, as well as electromagnetic radiation, and relates fields to their sources.
The material uses the material equations of the electromagnetic field, with the electric induction vector D
is expressed through the electric constant, the electric field strength vector
E
and the electric polarization vector
P
: D = ε 0 E + P. \mathbf{D} = \varepsilon_0 \ \mathbf{E} + \mathbf{P}.
As a rule, we can assume that P = ε 0 χ E \mathbf P = \varepsilon_0 \chi \mathbf E , where the quantity χ \chi is a tensor and is called electrical polarizability. This expression means that the electric polarization vector, as a certain reaction of a substance, is generated by the electric field strength vector in the substance, and the directions of these vectors may not coincide.
In a weak field, the quantity χ\chi has a special name - dielectric susceptibility and is almost constant, depending on the type of substance and its state. In this case, we can write: D = ε 0 E + ε 0 χ E = ε 0 ( 1 + χ ) E = ε 0 ε r E = ε a E . \mathbf{D} = \varepsilon_0 \ \mathbf{E} + \varepsilon_0 \chi \mathbf E= \varepsilon_0 (1+\chi) \mathbf E= \varepsilon_0 \varepsilon_r \mathbf E= \varepsilon_a \mathbf E.
The product of the electrical constant and the relative dielectric constant ε r \varepsilon_r in this expression is called the absolute dielectric constant ε a \varepsilon_a.
The electric constant is included in the expression of Coulomb's law, which gives an expression for the force acting between two electric charges: F 12 = q 1 q 2 4 π ε 0 r 12 2 r 12 r 12 , \mathbf{F}_{12}=\frac {q_1 q_2}{4\pi\varepsilon_0 r_{12}^2} \frac{\mathbf{r}_{12}}{r_{12}},
where r 12 r_{12} is the distance between charges q 1 q_1 and q 2 q_2. If r 12 \mathbf{r}_{12} is a vector directed from the charge q 1 q_1 to the charge q 2 q_2 , then the force F 12 \mathbf{F}_{12} will be the force acting on the charge q 2 q_2 with charge side q 1 q_1 . The expression for force shows that the electrical constant in the SI system of physical units relates electric charge to mechanical units such as force and distance.