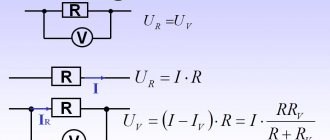3.9
Average rating: 3.9
Total ratings received: 91.
3.9
Average rating: 3.9
Total ratings received: 91.
Electric current is the ordered movement of electrical charges or charged macroscopic bodies. The direction of the electric current I coincides with the direction of movement of positively charged particles: the charges move under the influence of the electric field that is created in the conductor as a result of the voltage U applied to the ends of the conductor. How does the magnitude of the current depend on the magnitude of the voltage? Let's try to figure it out.
Current value
By definition, current strength is a physical quantity equal to the amount of charge q passing through the cross section of the conductor during time t:
$$ I = { q\over t } $$
If the current strength does not depend on time, then such an electric current is called constant. Let us further consider just such a case when the current is constant. It is extremely difficult to measure the amount of charge, so in 1826 the German physicist Georg Ohm did the following: in an electrical circuit consisting of a voltage source (battery) and resistance, he measured the amount of current at different resistance values. Then, without changing the resistance value, he began to change the parameters of the voltage source, connecting, for example, two or three sources at once. By measuring the current in the circuit, he obtained the dependence of the current on the voltage U and on the resistance R.
Rice. 1. Current and voltage measurement circuit by Georg Ohm.
Exercises
Exercise No. 1
When the voltage at the ends of the circuit section is equal to $2 \space V$, the current strength in the conductor is $0.4 \space A$.
What should the voltage be so that the current in the same conductor is $0.8 \space A$? Given: $U_1 = 2 \space B$ $I_1 = 0.4 \space A$ $I_2 = 0.8 \space A$
$U_2 — ?$
Show solution and answer
Hide
Solution:
We know that voltage and current are directly proportional to each other . This means that by how many times the current strength increases, the voltage will increase by the same amount.
Let's see how many times the current strength has increased: $\frac{I_2}{I_1} = \frac{0.8 \space A}{0.4 \space A} = 2$.
It turns out that the current strength has doubled. This means that the voltage will also double: $U_2 = 2 \cdot U_1 = 2 \cdot 2 \space V = 4 \space V$.
Answer: $U_2 = 4 \space В$.
Ohm's law
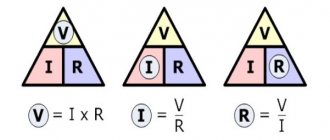
As a result of his research, Georg Ohm discovered that the ratio of the voltage U between the ends of a metal conductor, which is part of an electrical circuit, to the current strength I in the circuit is a constant value:
$$ R= { U \over I } $$
where R is electrical resistance. This formula is called Ohm's law, which is still the main calculation tool in the design of electrical and electronic circuits.
If we plot the voltage values along the abscissa axis, and the current values in the circuit at given voltage values along the ordinate axis, we will get a graph of the dependence of the current I on the voltage U.
Rice. 2. Graph of current versus voltage.
From this graph it is clear that this relationship is linear. The angle of inclination of the straight line depends on the amount of resistance. The larger R, the smaller the angle of inclination.
Rice. 3. Graph of current versus resistance.
If we fix the voltage U and plot the values R of the electrical resistance along the abscissa axis, then the resulting graph shows that this dependence is already nonlinear - with increasing resistance, the behavior of the current is described by an inversely proportional function - a hyperbola.
Ohm's law stops working at high current values, as additional effects associated with thermal heating of the substance and an increase in temperature begin to operate. In gases at high currents, breakdown occurs, the current grows like an avalanche, deviating from the linear law.
General information
In the 16th century, scientific research showed that there is something in nature that can cause interaction forces between bodies. Subsequently, this phenomenon was called electricity, and the quantity characterizing the process was called charge. In 1729, Charles Dufay discovered the existence of two types. Those of the same type have the property of repelling each other, and those of the same type have the property of attraction. They are conventionally divided into positive and negative.
Essentially, electric charge determines the ability of a substance to generate a field and take part in electromagnetic interaction. The SI unit of measurement of a scalar quantity is the coulomb [C]. Charge carriers are elementary particles. They are designated using the symbol q.
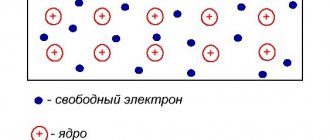
The physical body consists of atoms or molecules . In turn, they are formed from the simplest particles. A solid contains nuclei consisting of protons and neutrons. Electrons rotate around them in orbitals. If no external forces act on the body, the system is in electrical equilibrium. This is due to the fact that the positive charge of the nucleus is compensated by the negative charge of the electron.
But at the same time, so-called free electrons can exist in the body. These are particles that have no connection with the nucleus and move freely throughout the body. Their movement is chaotic. Moving along the crystal lattice, electrons collide with defects and impurities, giving them some of their energy and converting it into heat. But this phenomenon is so insignificant that it is difficult to detect even with specialized devices.
If an electromagnetic field is applied to the body, the movement of free charges becomes directed. When ensuring its continuity, a phenomenon occurs that is called electric current. Thus, it came to be understood as the ordered movement of charge carriers. Research has shown that such particles can be:
- electrons are solids;
- ions - gases, electrolytes.
To describe electric current, two quantities are used - work and force. The first shows how much energy must be expended to transfer a charge from one point in the field to another. They call it tension. The strength of the current is determined by the ratio of the amount of charge passing through the cross section of the body per unit time.
Units
In the International System of Units (SI), the unit of electrical resistance is called the “ohm” in honor of the physicist Georg Ohm. By definition, an electrical resistance of 1 ohm has a section of the circuit where the voltage drops 1 V at a current of 1 A.
$$ [1 Ohm] ={ [1 V]\over [1 A] } $$
The unit of measurement of resistivity is derived from the units of quantities included in the formula: resistance, length and area. That is, in the SI system it turns out that if R = 1 Ohm, S = 1 m2, and L = 1 m, then ρ = 1.
This is the unit of measurement for resistivity. But in practice it turned out that real wires have a cross-sectional area of much less than 1 m2. Therefore, when calculating ρ, it was decided to use the value of the area S in mm2 so that the final value has a compact form. Then we get more convenient (fewer zeros after the decimal point) numerical values of resistivity for perception:
$$ [ ρ ] = { [Ohm] * [mm^2] \over [m]} $$
The current value is measured with an ammeter, and the voltage value with a voltmeter. When making very accurate measurements, it is necessary to take into account the internal resistance of these devices.
Concept of potential, potential difference
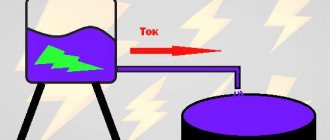
Closely related to the concept of electric current voltage is the concept of “potential”, or “potential difference”. Okay, let's go back to our plumbing analogy.
Our tank is located on a hill, which allows water to flow down the pipe freely. Since the water tank is at a height, the potential of this point will be higher or more positive than that at ground level. Do you see what happens?
We now have two points with different potentials, or rather different potential values.
It turns out that in order for electric current to flow through a wire, the potentials must not be equal. Current runs from a point with a higher potential to a point with a lower potential.
Remember this expression that current runs from plus to minus. So this is all the same. Plus is a more positive potential and minus is more negative.
By the way, do you want a question for backfilling? What will happen to the current if the potentials change places periodically?
Then we will observe how the electric current changes its direction to the opposite each time the potentials change. This will turn out to be alternating current. But we won’t consider it for now, so that a clear understanding of the processes can form in our heads.
Voltage.
By definition, voltage is the energy (or work) expended in moving a unit positive charge from a point of low potential to a point of high potential (i.e., the first point has a more negative potential compared to the second). We remember from the physics course that the potential of an electrostatic field is a scalar quantity equal to the ratio of the potential energy of a charge in the field to the magnitude of this charge. Let's look at a small example:
There is a constant electric field in space, the intensity of which is equal to E. Consider two points located at a distance d from each other. So the voltage between two points is nothing more than the potential difference at these points:
U = \phi_1\medspace-\medspace \phi_2
At the same time, do not forget about the connection between the electrostatic field strength and the potential difference between two points:
\phi_1\medspace-\medspace \phi_2 = Ed
And as a result, we get a formula connecting stress and tension:
U = Ed
In electronics, when considering various circuits, voltage is still considered to be the potential difference between points. Accordingly, it becomes clear that voltage in a circuit is a concept associated with two points in a circuit. That is, to say, for example, “voltage in a resistor” is not entirely correct. And if they talk about voltage at some point, then they mean the potential difference between this point and the “ground”. This is how we smoothly arrived at another commonly used concept, namely the concept of “earth”. So, “ground” in electrical circuits is most often considered to be the point of zero potential (that is, the potential of this point is 0).
Let's say a few more words about units that help characterize the magnitude of voltage . The unit of measurement is Volt (V). The classic quantitative definition of a value of 1 Volt sounds like this: to move a charge of 1 Coulomb between points having a potential difference of 1 Volt, it is necessary to do work equal to 1 Joule. With this, everything seems to be clear and you can move on.
And next we have another fundamental concept, namely current.
Answers
Series and parallel connections of conductors →
← Electric field. The effect of an electric field on electric charges. Conductors and dielectrics
Constant electric current. Current strength. Voltage. Electrical resistance. Ohm's law for a section of an electrical circuit
3 (60.8%) 25 votes
Problem solving
Problems associated with finding fundamental electrical quantities are usually simple. But to solve them you will need not only to know several formulas, but also SI units of measurement. In the International System, current is measured in amperes, voltage in volts, resistance in ohms, and power in watts. Often you have to deal with large numbers or, conversely, small ones, so to simplify the notation, prefixes are used: micro, nano, kilo, mega.
Here are some of the typical tasks designed for independent study as part of physics lessons for grade 8:
- Determine the voltage across a resistor with a resistance of 10 ohms if a current of 1 ampere passes through it. This is a simple example solved using Ohm's law. According to him, I = U/R, therefore: U= I*R. Substituting the original data, you can perform the following calculations: U= 1 A*10 Ohm = 10 V.
- Find the power of the device if its resistance is 1 kOhm, when the potential difference created is 10 volts. To calculate P, you need to determine the current consumption: I = U/R = 10/1000 = 0.01 A. Now, using the power formula, you can find the desired parameter: P = I*U = 0.01*10 = 0.1 W .
- An electric lamp is connected to a network with a voltage of 220 V. Find the value of the current passing through the spiral if the conductor resistance is 30 Ohms. According to the law: I = U/R = 220/3 = 7.3 A.
- At a voltage of 220 volts, the current passing through the inductor is 5 A. Calculate how I will change if the voltage increases by 20 volts. Based on the fact that the resistance is constant, we can create a proportion: U1 / I1 = U2/I2. The voltage for the second case can be determined from the expression: U 2 = U + U 1 = 220 + 20 = 240 V. Hence I2 = I1 * U2 / U 1 = 5 A * 240 V / 220 V = 5.45 A.
The formula for the dependence of current on voltage, obtained experimentally, has become fundamental in the development of electrical engineering and electronics. The relationship between the quantities turned out to be proportional, taking into account a coefficient called resistance. Moreover, its value depends on the type of material and body size.
Voltage value for some devices and natural phenomena
Table 1 provides some voltage values for your reference.
| Device | $U$, $B$ |
| Galvanic cell | 1,25 |
| City power grid | 220 |
| Electric lamps | 20 — 250 |
| TV | 100 — 600 |
| Fridge | 150 — 600 |
| Computer | 400 — 750 |
| Iron | 500 — 2000 |
| Electric motors | 550 — 1700 |
| Heater | 1000 — 2400 |
| Air conditioner | 1000 — 3000 |
| A circular saw | 1800 — 2100 |
| High pressure pump | 2000 — 2900 |
| High-voltage power lines (PTL) | 500 000 |
| Lightning strike | Up to 1,000,000 |
Table 1. Voltage in some technical devices and nature
Dangerous and safe voltage values
Everyone knows that high (high) voltage is life-threatening. Let's make a simple analogy for better understanding.
For example, the voltage between a high-voltage transmission line wire and ground is $100 \space 000 \space V$. Let's connect this wire to ground. It turns out that when a charge of only $1 \space K$ passes through it, work of $100 \space 000 \space J$ is done. The same work will be done by a load weighing $1000 \space kg$ if it falls from a height of $10 \space m$. Similar damage can be caused by high voltage.
Typically, a voltage of no more than $42 \space V$ is considered safe . Such voltage is created, for example, by galvanic cells.
Many people probably remember how, as a child, their parents forbade putting their fingers into a socket. And it’s better not to disassemble it yourself. It is better to entrust such work to specialists. Why? The current in such a network comes from generators, and the voltage is usually $220 \space V$. Such tension can cause significant harm to health.
INFOFIZ
Conductors differ from dielectrics in that they contain free charges that can move throughout the entire volume of the conductor.
If an insulated conductor is placed in an electric field, then the free charges q
a force will act in the conductor. As a result, a short-term movement of free charges occurs in the conductor. This process will end when the own electric field of the charges arising on the surface of the conductor does not completely compensate for the external field. The resulting electrostatic field inside the conductor is zero.
However, in conductors, under certain conditions, continuous ordered movement of free electric charge carriers can occur. This movement is called electric current
.
Electric current is
the ordered movement of charged particles.
The direction of
the electric current is taken to be the direction of movement of positive free charges.
In metals, charge carriers are electrons - negatively charged particles, therefore the electric current in metals is always directed against the movement of electrons.
The quantitative measure of electric current is the current strength
I.
Current strength
–
a scalar physical quantity equal to the ratio of the charge q transferred through the cross section of the conductor during the time interval t to this time interval: The
current strength is numerically equal to the number of charges passing through the cross section of the conductor in 1 second.
Ordered movement of electrons in a metal conductor I - current strength, S
– cross-sectional area of the conductor, – electric field.
The SI unit of current is the ampere.
[A].
A device for measuring current is called an ammeter.
The ammeter is connected in series
into an open circuit so that the entire measured current passes through it.
On electrical circuit diagrams, the ammeter is designated .
The ammeter has some internal resistance RA
. The internal resistance of the ammeter must be small enough compared to the total resistance of the entire circuit.
If the strength of the current and its direction do not change over time, then such a current is called constant .
A short-term current in a conductor can be obtained by connecting two charged conducting bodies that have different potentials with this conductor. The current in the conductor will disappear when the potential of the bodies becomes the same. For the existence of electric current
In a conductor, it is necessary to create an electric field in it and maintain it for a long time
.
Conditions for the existence of electric current:
1. The presence of free charges inside the conductor,
2. The presence of a potential difference at the ends of the conductor (creation of an electric field inside the conductor)
Electric current is the ordered movement of charged particles, which is created by an electric field, and at the same time it does work. Current work is the work done by the electric field forces that create an electric current.
Direct electric current can only be created in a closed circuit
, in which free charge carriers circulate along closed trajectories.
When an electric charge moves in an electrostatic field along a closed path, the work done by electric forces is zero. Therefore, for the existence of direct current, it is necessary to have a device in the electrical circuit that is capable of creating and maintaining potential differences in sections of the circuit due to the work of forces of non-electrostatic origin
. When a single positive charge moves along a certain section of the circuit, work is performed by both electrostatic (Coulomb) and external forces.
The work of electrostatic forces when moving a unit charge is equal to the potential difference Δφ12 = φ1 – φ2 between the initial (1) and final (2) points of the inhomogeneous section. U value
12 is usually called
the voltage
in circuit section 1–2.
Voltage is a physical quantity that characterizes the action of an electric field on charged particles; it is numerically equal to the work of the electric field to move a charge from a point with potential φ1 to a point with potential φ2.
In the case of a homogeneous area, the voltage is equal to the potential difference: U12 = φ1 – φ2
The SI unit of voltage is the volt.
[IN].
A device for measuring voltage is called a voltmeter.
A voltmeter
is designed to measure the potential difference applied across its terminals
.
It is connected in parallel
to the section of the circuit on which the potential difference is measured.
On electrical circuit diagrams, the ammeter is designated .
Any voltmeter has some internal resistance RB
.
In order for the voltmeter not to introduce a noticeable redistribution of currents when connected to the circuit being measured, its internal resistance
must be
large
compared to the resistance of the section of the circuit to which it is connected. Since there are no external forces acting inside the voltmeter, the potential difference at its terminals coincides, by definition, with the voltage. Therefore, we can say that a voltmeter measures voltage.
Just as friction in mechanics prevents movement, the resistance of a conductor creates opposition to the directional movement of charges and determines the conversion of electrical energy into the internal energy of the conductor. Reason for resistance: collision of freely moving charges with ions of the crystal lattice.
The quantity characterizing the resistance to electric current in a conductor, which is determined by the internal structure of the conductor and the chaotic movement of its particles, is called
the electrical resistance of the conductor.
The SI unit of electrical resistance of conductors is the ohm
[Ohm]. A resistance of 1 ohm has a section of the circuit in which a current of 1 A occurs at a voltage of 1 V.
The electrical resistance of a conductor depends on
the size
and
shape of the conductor and the material
which
the conductor is made
.
S – cross-sectional area of the conductor l –
conductor length ρ – conductor resistivity.
The resistance of a conductor is directly proportional to its length and inversely proportional to its cross-sectional area.
The value ρ, which characterizes the dependence of the resistance of a conductor on the material from which it is made and on external conditions, is called the resistivity of the conductor. It is numerically equal to the resistance of a conductor with a length of 1 m and a cross-sectional area of 1 mm2, made of this substance. SI unit of resistivity [1 Ohm*m = 1 Ohm*mm2/m]
The conductor resistance depends
and on its condition, namely
on temperature
.
This dependence is expressed by the formula or
α is the temperature coefficient of resistance. For all pure metals.
When pure metals are heated, their resistance increases, and when cooled, their resistance decreases.
.
Ohm's law for a section of a circuit.
The German physicist G. Ohm in 1826 experimentally established that the current strength I
, flowing along a homogeneous metal conductor (that is, a conductor in which no external forces act), is proportional to the voltage
U
at the ends of the conductor:
This relationship expresses Ohm's law for a homogeneous section of the chain:
The current in a conductor is directly proportional to the applied voltage and inversely proportional to the resistance of the conductor.
A conductor with electrical resistance is called a resistor
.
Conductors that obey Ohm's law are called linear
.
The graphical dependence of the current I on the voltage U
is called the current-voltage characteristic
(abbreviated as VAC). It is represented by a straight line passing through the origin.
Based on the current-voltage characteristic of a conductor, one can judge its resistance: the greater the angle of inclination of the graph to the voltage axis, the lower the resistance of the conductor.