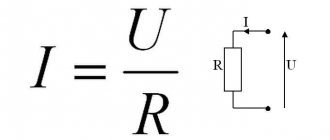Electrical engineering as a field of science dealing with the use of electricity, including its production, distribution and accounting, operates with the values of current, voltage, power and resistance. These are the basic quantities. In addition, there are many other characteristics and concepts, but within the framework of this article these fundamental concepts will be considered.
Variety of electrical engineering devices
Resistance
Current strength: formula
Any conductor in a circuit prevents current from passing through it. This characteristic defines such a physical quantity as resistance. Based on the resistance value, all substances are classified as conductors or insulators. The exact boundary is very vague, so under certain conditions some substances can be classified as both insulators and conductors. A section of an electrical circuit may have an element with a certain value, which is called a resistor.
Resistors of various types
Concept of potential
In order for electrons to pass through a circuit, energy is needed that can set them in motion along an electrical circuit. For example, in the case of static electricity, it is the force produced by an imbalance of electrical charge in objects.
A school experiment with rubbing an ebonite stick on wool illustrates the creation of an excess of electrons in ebonite (negative charge) and a deficiency of electrons in wool (positive charge) when mechanical energy is expended on rubbing.
This is the electric current in the circuit, and the degree of electrification of bodies is a quantity called potential. To simplify the understanding of what is called voltage, we can consider this value as the potential difference between objects.
Relationship between electrical circuit parameters
All parameters of any electrical circuit are strictly interconnected, so at any moment in time you can accurately determine the value of any of them, knowing the rest.
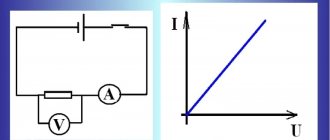
For your information. The fundamental law by which most calculations are made is Ohm's law, according to which the current strength is inversely proportional to its resistance and directly proportional to the applied potential difference.
Ohm's law and its founder
Ohm's law voltage formula is as follows:
I=U/R.
So, a circuit with a higher voltage passes more current, and at the same voltage the amperage will be greater where the resistance is lower.
The accepted notations in the formula for calculating voltage and current are understood throughout the world:
- I – current strength;
- U – voltage;
- R – resistance.
Using a simple mathematical transformation, a formula is found for calculating resistance through current and voltage.
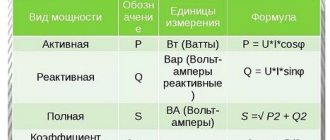
In addition to Ohm's law, the formula for calculating power is used:
P=U∙I.
The symbol P here indicates the current power.
Any circuit may contain sections where there is a serial connection, or there is an element connected in parallel. The calculations become more complicated, but the basic formulas remain the same.
Physical work of a test charge in an electric field
So, you have turned into a test electric charge
q,
many times smaller than the charge
Q
on the capacitor plates, and have begun your journey between the capacitor plates.
In this case, you will experience the action of Coulomb forces. Let's say that you are a negatively charged particle like an electron, then you will be attracted towards the +Q
-Q
plate . The closer you are to one of the plates, the stronger you will experience its force.
Let's assume that you entered the capacitor from the plate side -Q
and you immediately began to be pushed away from it towards the
+Q
.
You did not resist this influence and decided not to resist nature and move in complete agreement with the attraction. For these purposes, beams and stairs are conveniently located, along which you can freely reach the +Q
by any route.
Since the electric Coulomb force acts on you, you begin to freely pick up speed, as if you were being carried by the wind. As a result, you have covered the distance along the beam from one ladder to another in the direction from point A
to point
B
(
see picture above
).
Stairs are equipotential lines, and accordingly, you have covered the distance from one potential value to another. In our case, you moved from the potential that was larger for you to the one that was smaller. If you were a charge of a different sign, that is, +q
, then the potentials would change their signs and the larger one would become smaller, and the smaller one would become larger.
Mathematically, this means multiplying the potentials by -1
.
A force acted on you and you moved from point A
to point
B
, in other words, you moved from
potential φa
(larger) to
potential φb
(smaller).
It's like floating down a river on a raft, where you don't have to row oars and don't need a motor to propel you. We can say that you have done mechanical work, which is calculated as the product of force and distance. Having made such a movement, you lost some of the potential energy, which turned into kinetic energy (the speed of your movement), and then was probably released in the form of heat during braking. Having made the return journey from point B
to point
A
, you will move against the flow, as it were, you will have to expend energy, row with oars, use a motor, etc. By moving back you will increase your potential energy, because you will move to a point with greater potential and your energy state will increase.
The difference between these two potentials φa
and
φb
and will be the electrical voltage. These are equivalent concepts, but in practical electrical engineering the expression most often used is not potential difference, but voltage. When considering electrical circuits, the expression used is the voltage drop across a section of the circuit, and for sources of electricity, the same potential difference is defined as electromotive force (EMF).
Potential difference Δφ=φ1-φ2
always shows what work
A
can be done by a charge carrier
q
when moving this charge from a point with one potential
φ1
to a point with another potential
φ2
.
When calculating, you must keep in mind that potentials can have either a plus
or a
minus
.
If a charge needs to expend energy for such a movement, and therefore increase its potential, then work A
will have a sign (-), and if the charge carrier moves from a region of high potential to a region of low potential, then energy is released and work
A
will have a sign (+).
Thus, electric voltage is an energy characteristic
of the electric field and represents a potential difference
Δφ
.
This means that it is fundamentally incorrect to say that voltage is potential. Electric voltage is always a potential difference and it is only possible between two points of the electric field. If there is one point in the space of the electric field, then it is appropriate to talk only about the potential of this point, but not about its voltage.
It is necessary to be absolutely clear about the differences between such concepts as: electric field strength E
, potential
φ
, and, of course, potential difference - electrical voltage. Having understood these differences, it will be quite easy to understand what electric current is.
How the law works in real life
Using the power calculation formula and Ohm's law together, you can make calculations without knowing one of the quantities. The simplest example is that for an incandescent lamp only its power and voltage are known. Using the above formulas, you can easily determine the parameters of the filament and the current through it.
Incandescent lamp
Current formula through power:
I=P/U;
Resistance:
R=U/I.
The same result can be found from the power without resorting to intermediate calculations:
R=U2/P.
Similarly, you can calculate any quantity knowing only two of them. To simplify transformations, there is a mnemonic display of formulas that allows you to find any quantities.
Rule for remembering calculations
Looking carefully at the formulas, you can see that if you reduce the voltage on the lamp by half, the expected power will not decrease by the same factor by half, but by four, according to the formula:
P=U2/R.
This is a fairly common mistake among people who are far from electrical engineering, who incorrectly correlate power and voltage, as well as their effect on other parameters.
By the way. The current found through resistance and voltage is valid for both direct and alternating current, as long as it does not use elements such as a capacitor or inductance.
You can make calculations easier by using an online calculator.
Characteristic values and standards
| An object | Voltage type | Value (at consumer input) | Value (at source output) |
| Electrocardiogram | Pulse | 1-2 mV | — |
| TV antenna | Variable high frequency | 1—100 mV | — |
| Galvanic zinc cell type AA (“finger”) | Permanent | 1.5 V | — |
| Lithium Galvanic Cell | Permanent | 3—3.5 V (finger-type element, using the example of Varta Professional Lithium, AA) | — |
| Logic signals of computer components | Pulse | 3.5 V; 5 V | — |
| Battery type 6F22 (“Krona”) | Permanent | 9 V | — |
| Power supply for computer components | Permanent | 5 V, 12 V | — |
| Electrical equipment of cars | Permanent | 12/24 V | — |
| Power supply for laptop and LCD monitors | Permanent | 19 V | — |
| "Safe" reduced voltage network for operation in hazardous environments | Variable | 36-42 V | — |
| Voltage of the most stable burning of Yablochkov candles | Permanent | 55 V | — |
| Voltage in the telephone line (with the handset on-hook) | Permanent | 60 V | — |
| Japan power grid voltage | AC three-phase | 100/172 V | — |
| US Home Electrical Voltage | AC three-phase | 120 V / 240 V (split phase) | — |
| Voltage in household electrical networks in Russia | AC three-phase | 220/380 V | 230/400 V |
| Electric ramp discharge | Permanent | up to 200-250 V | — |
| Tram and trolleybus contact network | Permanent | 550 V | 600 V |
| Electric eel discharge | Permanent | up to 650 V | — |
| Metro contact network | Permanent | 750 V | 825 V |
| Contact network of an electrified railway (Russia, direct current) | Permanent | 3 kV | 3.3 kV |
| Low power overhead power distribution line | AC three-phase | 6—20 kV | 6.6—22 kV |
| Power station generators, powerful electric motors | AC three-phase | 10—35 kV | — |
| At the anode of the kinescope | Permanent | 7—30 kV | — |
| Static electricity | Permanent | 1—100 kV | — |
| On a car spark plug | Pulse | 10-25 kV | — |
| Contact network of the electrified railway (Russia, alternating current) | Variable | 25 kV | 27.5 kV |
| Air breakdown at a distance of 1 cm | 10-20 kV | — | |
| Ruhmkorff coil | Pulse | up to 50 kV | — |
| Breakdown of a 1 cm thick layer of transformer oil | 100-200 kV | — | |
| High power overhead power line | AC three-phase | 35 kV, 110 kV, 220 kV, 330 kV | 38 kV, 120 kV, 240 kV, 360 kV |
| Electrophore machine | Permanent | 50—500 kV | — |
| Ultra-high voltage overhead power line (inter-system) | AC three-phase | 500 kV, 750 kV, 1150 kV | 545 kV, 800 kV, 1250 kV |
| Tesla Transformer | Pulse high frequency | up to several MV | — |
| Van de Graaff generator | Permanent | up to 7 MV | — |
| thunder cloud | Permanent | From 2 to 10 GV | — |
Example with ordinary water
There are substances that can be classified as both conductors and insulators. The simplest example is ordinary water. Distilled water is a good insulator, but the presence of almost any impurities in it makes it a conductor. This especially applies to salts of various metals. When dissolved in water, salts dissociate into ions, their presence is a direct reason for the occurrence of current. The higher the concentration of salts, the less resistance the water will have.
Dependence of water resistance on salt content
For clarity, you can take distilled water to prepare electrolyte for car batteries. By lowering the ohmmeter probes into water, you can see that its readings are high. The addition of just a few crystals of table salt after a while causes a sharp decrease in resistance, which will be smaller the more salt goes into solution.
What is EMF
What is EMF, do you think? I'll tell you now!
Electromotive force (EMF) is also measured in Volts, like voltage.
Let's take a device that measures volts (voltmeter), a battery and take a measurement.
The device shows 1.5 Volts and this is not voltage, but electromotive force (EMF).
Now let’s connect the light bulbs to the battery.
Measuring voltage in various parts of an electrical circuit.
We noticed that on one light bulb the voltage (not EMF) is 1 Volt, and on the other 0.3 Volts
The voltage on the light bulbs depends on their power. Power is measured in Watts.
Power=Voltage*Current (P=U*I)
The higher the power of the light bulb, the higher the voltage will be on it.
If our battery is 1.5 volts = 1 volt +0.3 volts = 1.3 volts, where did the 0.2 volts go? The battery also has its own internal resistance, so that’s where they went.
Various quantities used
In addition to the basic quantities: volts, amperes, ohms, watts, multiples, larger or smaller, are used. The following prefixes are used for designations:
- Kilo – 1000;
- Mega – 1000000;
- Giga – 1000000000;
- Milli – 0.001.
Thus it turns out:
- Kilovolt (kV) – thousand volts;
- Megawatt (MW) – million watts;
- Milliohm (mOhm) – one thousandth of an ohm;
- Gigawatt (GW) – a thousand megawatts or a billion watts.
How to find voltage
The formula for finding voltage as a potential difference in an electric field:
U=ϕA-ϕB, where ϕA and ϕB are potentials at points A and B, respectively.
You can also write voltage as the work done to transfer a unit of charge from point A to point B in an electric field:
U=A/q, where q is the amount of charge.
The greater the work, the higher the electric field strength E, that is, the force acting on a stationary charge.
The potential energy of a charge in an electrostatic field is called electrostatic potential.
Galvani Potential
Within a conducting material, the energy of an electron is influenced not only by the average capabilities, but also by the particular thermal and atomic environment in which it is found. When a voltmeter is connected between two different types of metal, it does not measure the difference in electrostatic potential.
The quantity measured by a voltmeter is negative and is usually called the voltage difference. While the net uncorrected electrostatic capability (not measured by a voltmeter) is sometimes called Galvanic. The terms "voltage" and "electric potential" are ambiguous in the sense that in practice they can refer to either in different contexts.
Hydraulic analogy
To make it easier to understand the laws of electrical circuits, you can imagine an analogy with a hydraulic system, in which the connection of the pump and pipelines forms a closed system. To do this, the following correspondences are needed:
- Power source – pump;
- Conductors – pipes;
- Electric current is the movement of water.
Without much effort, it becomes clearer that the smaller the diameter of the pipes, the slower the water moves through them. The more powerful the pump, the more water it can pump. With the same pump power, reducing the diameter of the pipes will lead to a decrease in water flow.
Hydraulic analogy
The essence of the phenomenon
Voltage is the electrical driving force that is designed to push free types of electrons from one atom to another in a certain direction. A mandatory requirement for the flow of charges is the presence of a circuit with a closed loop, which creates the conditions for them to move. If there is a break in the electrical circuit, then the process of directional movement of particles stops.
Note! It is worth noting that the unit of voltage in an electrical circuit depends on the material of the conductor, how the load is connected, and what the temperature is. What it is
What it is
Measuring instruments
Measuring instruments are used to measure the parameters of electrical circuits:
- Voltmeter;
- Ammeter;
- Ohmmeter.
The most commonly used class of combined devices in which the measured value is selected by a switch is ampere-volt-ohmmeters or avometers.
One of the most common avometers