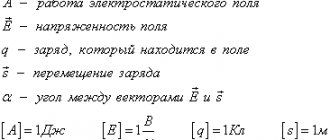Unified State Exam 2022 in Physics ›
Electrodynamics is a branch of physics that studies the properties and interactions of electric charges carried out through an electromagnetic field.
Electrostatics is the branch of electrodynamics that examines the properties and interactions of stationary electrically charged bodies or particles.
Electromagnetic interaction is the interaction between electrically charged particles or macrobodies.
A point charge is a charged body whose size is small compared to the distance at which its action is assessed.
Electrification of bodies
Electrification is the process of imparting an electric charge to the body, i.e., violating its electrical neutrality. The process of electrification is the transfer of electrons or ions from one body to another. As a result of electrification, the body gains the opportunity to participate in electromagnetic interaction.
Methods of electrification:
- friction, for example, electrification of an ebonite stick when rubbing against fur. When two bodies come into close contact, some electrons transfer from one body to another; As a result, a deficiency of electrons is created on the surface of one of the bodies and the body receives a positive charge, while the other has an excess, and the body becomes negatively charged. The charges of the bodies are the same;
- through influence (electrostatic induction) - the body remains electrically neutral, the electric charges inside it are redistributed so that different parts of the body acquire charges of different signs;
- When a charged and uncharged body comes into contact, the charge is distributed between these bodies in proportion to their sizes. If the sizes of the bodies are the same, then the charge is distributed equally between them;
- upon impact;
- under the influence of radiation - under the influence of light, electrons can escape from the surface of the conductor, and the conductor acquires a positive charge.
Short-range theory
According to the theory of short-range interaction, electric charges transmit their interactions with the help of special material intermediary particles and are produced at a finite speed.
The founders of the theory of short-range action in classical physics are the philosopher and physicist Rene Descartes and the natural scientist Michael Faraday. Within the framework of this concept, it is generally accepted that particles, which are intermediaries in the process of transferring interactions, move at a strictly defined speed, which tends to the speed of light.
Carriers, or intermediary bodies that transmit the interaction of charges, are electric field quanta moving at the speed of light.
Short-range theory
Interaction of charges. Two types of charges
Electric charge is a scalar physical quantity that characterizes the ability of a body to participate in electromagnetic interactions.
Designation – \( q \), SI unit of measurement – pendant (C).
There are two types of electrical charges: positive and negative. The electron has the smallest negative charge (–1.6·10-19 C), the smallest positive charge (1.6·10-19 C) has the proton. The minimum charge that can be imparted to a body is equal to the charge of an electron (elementary charge). If a body has excess (extra) electrons, then the body is negatively charged, if the body has a lack of electrons, then the body is positively charged.
The amount of charge on the body will be equal to
where \( N \) is the number of excess or missing electrons; \( e \) - elementary charge equal to 1.6·10-19 C.
Important! A particle may have no charge, but charge does not exist without a particle.
Electric charges interact:
- charges of the same sign repel:
- charges of opposite signs attract:
The device for detecting electric charge is called an electroscope. The main part of the device is a metal rod on which two sheets of metal foil are attached, placed in a glass vessel. When a charged body comes into contact with the electroscope rod, the charges are distributed between the sheets of foil. Since the charge of the leaves is of the same sign, they repel each other.
An electrometer can also be used to measure charges. Its main parts are a metal rod and an arrow, which can rotate around a horizontal axis. The rod with the arrow is fixed in a plastic sleeve and placed in a metal case covered with glass covers. When a charged body comes into contact with a rod, the rod and the arrow receive electric charges of the same sign. The arrow rotates at a certain angle.
Law of conservation of electric charge
A system is called closed (electrically isolated) if there is no exchange of charges with the environment.
In any closed (electrically isolated) system, the sum of electric charges remains constant regardless of any interactions within it.
The total electric charge \( (q) \) of the system is equal to the algebraic sum of its positive and negative charges \( (q_1, q_2 … q_N) \):
Important! In nature, charges of the same sign do not arise or disappear: positive and negative charges can mutually neutralize each other if they are equal in magnitude.
Coulomb's law
Coulomb's law was discovered experimentally: in experiments using torsion balances, the interaction forces of charged balls were measured.
Coulomb's law is formulated as follows: the force of interaction \( F \) of two point stationary electric charges in a vacuum is directly proportional to their modules \( q_1 \) and \( q_2 \) and inversely proportional to the square of the distance between them \( r \ ):
where \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (N m2)/Cl2 – proportionality coefficient, \( \varepsilon_0=8.85\cdot10^{- 12} \) C2/(N m2) – electrical constant.
The coefficient \( k \) is numerically equal to the force with which two point charges of 1 C each interact in a vacuum at a distance of 1 m.
The Coulomb force is directed along the straight line connecting the interacting charges. Charges interact with each other with forces equal in magnitude and opposite in direction.
The value of the Coulomb force depends on the environment in which they are located. In this case, the formula of the law is:
where \( \varepsilon \) is the dielectric constant of the medium.
Coulomb's law applies to interactions
- stationary point charges;
- uniformly charged spherical bodies.
In this case, \( r \) is the distance between the centers of the spherical surfaces.
Important! If the charged body is extended, then it is necessary to split it into point charges, calculate the forces of their pairwise interaction and find the resultant of these forces (superposition principle).
Technological lesson map
| Lesson stage, time | Teacher activities | Student activity | Formed UUD | Forms of work (individual, group, frontal) | Means of education |
| 1. Organizational moment. 1 minute. | Greets students. | Respond to the teacher's greeting. | Communication | frontal | |
| 2. Setting goals and objectives for the lesson 2 minutes. | Preparing to understand goals and objectives creates motivation | Set lesson goals. | Regulatory | frontal | |
| 3.Updating students' basic knowledge. 3 minutes. | Conversation, frontal survey | Answer the questions asked. | Subject, regulatory | frontal | |
| 4.Primary assimilation of new knowledge. 15 minutes | 1.Demonstration of experience No. 1. Electroscopes are connected by a conductor | They follow the experiment and draw a conclusion. | Subject, regulatory, communicative | individual, group, frontal | Presentation |
| 2. Formulation of the concept of electric current. (slide No. 2) | They try to formulate a definition on their own and write it down in a notebook. | ||||
| 3. Clarification of the conditions for the long-term existence of electric current. | Draw a diagram | ||||
| 4.Demonstration of experiments with electric current sources . №2.Electrophoric machine (slide No. 9) generator (slide No. 10) | They follow the experiments, draw conclusions and write them down in a notebook. | ||||
| №3.Thermocouple (slide No. 12) | write down in a notebook. | ||||
| №4.Photo effect (slide No. 14) | write down in a notebook. | ||||
| Experiment 1 | Perform an experiment. They draw conclusions. | ||||
| A story about a galvanic cell. | EOR | ||||
| 4. Initial check of understanding. 5 minutes | A story about EOR batteries | Working with a textbook. Answer questions. | Subject, regulatory | individual, frontal | EOR |
| Dynamic pause. Snowman. 2 minutes | Doing exercises | Personal | individual, | Presentation | |
| 5.Primary consolidation. Test. 5 minutes | Hands out task cards. | Perform the test. | Subject, regulatory | Individual | Task cards |
| 6. Monitoring of learning, discussion of mistakes made and their correction. 3 minutes | Corrects errors. | Peer review. Grading. | Subject, regulatory | Individual | |
| 7.Reflection. 2 minutes | Summarizing the lesson, suggests self-assessment of achievements. | Participate in a conversation to discuss achievements. | Personal, communicative, regulatory | frontal | |
| 8. Information about homework. 2 minutes | Informs about homework. Distributes instructions for implementation | Write down homework. | Regulatory | frontal |
The effect of an electric field on electric charges
An electric field is a special form of matter that exists around electrically charged bodies.
The concept of an electric field was first introduced by Faraday. He explained the interaction of charges as follows: each charge creates an electric field around itself, which acts with some force on the other charge.
The properties of the electric field are that it:
- financially;
- created by charge;
- detected by the effect on the charge;
- continuously distributed in space;
- weakens with increasing distance from the charge.
The action of a charged body on surrounding bodies manifests itself in the form of forces of attraction and repulsion, tending to rotate and move these bodies in relation to the charged body.
The force with which the electric field acts on the charge can be calculated using the formula:
where \( \vec{E} \) is the electric field strength, \( q \) is the charge.
Solving problems about point charges and systems that can be reduced to them is based on the application of the laws of mechanics, taking into account Coulomb's law and the consequences arising from it.
Algorithm for solving problems about point charges and systems that can be reduced to them:
- make a drawing; indicate the forces acting on a point charge placed in an electric field;
- write down the equilibrium condition for the charge or the basic equation of the dynamics of a material point;
- express the forces of electrical interaction through charges and fields and substitute these expressions into the original equation;
- if during the interaction of charged bodies a redistribution of charges occurs between them, add the equation of the law of conservation of charges to the compiled equation;
- write down all auxiliary conditions mathematically;
- solve the resulting system of equations for an unknown quantity;
- check the solution
Usage
The study of the properties of the electric field has opened up enormous opportunities for humanity. The ability of a field to move electrons in a conductor made it possible to create current sources.
Various equipment used in medicine, the chemical industry, and electrical engineering has been created based on the properties of electric fields. Devices are being developed for use in the field of wireless energy transmission to the consumer. An example would be wireless charging devices for gadgets. These are still only the first steps towards transmitting electricity over long distances.
Today, thanks to knowledge about the properties of the field form of matter, unique filters for water purification have been developed. This method turned out to be cheaper than using traditional replacement cartridges.
Unfortunately, sometimes you have to neutralize the forces of the fields. Possessing the ability to electrify objects within the range of action, electric fields create serious obstacles to the normal operation of radio-electronic equipment. Accumulated static electricity is often the cause of failure of integrated circuits and field-effect transistors.
Electric field strength
Electric field strength \( \vec{E} \) is a vector physical quantity equal to the ratio of the force \( F \) acting on a test point charge to the magnitude of this charge \( q \):
Designation – \( \vec{E} \), unit of measurement in SI – N/C or V/m.
The field strength of a point charge in vacuum is calculated by the formula:
where \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (N m2)/C2, \( q_0 \) – charge creating the field, \( r \) – the distance from the charge creating the field to this point.
The field strength of a point charge in a medium is calculated by the formula:
where \( \varepsilon \) is the dielectric constant of the medium.
Important! The electric field strength does not depend on the magnitude of the test charge; it is determined by the magnitude of the charge creating the field.
The direction of the voltage vector at a given point coincides with the direction of the force with which the field acts on a positive test charge placed at this point.
The electric field intensity line is a line whose tangent at each point is directed along the intensity vector \( \vec{E} \).
Electrostatic field strength lines begin at positive electric charges and end at negative electric charges, or go to infinity from a positive charge and come from infinity to a negative charge.
The distribution of tension lines around positive and negative point charges is shown in the figure.
By determining the direction of the vector \( \vec{E} \) at various points in space, one can imagine a picture of the distribution of electric field strength lines.
A field in which the intensity is the same in magnitude and direction at any point is called a uniform electric field. The electric field between two oppositely charged metal plates can be considered homogeneous. Tension lines in a uniform electric field are parallel to each other.
Detection methods
Human senses do not perceive electric fields. Therefore, we cannot see them, taste them or identify them by smell. The only thing a person can feel is the straightening of the hair along the lines of tension. We simply do not notice the presence of weak influences.
They can be detected through exposure to small pieces of paper, elderberry balls, etc. The electric field affects the electroscope - its petals react to such influences.
A very simple and effective detection method using a compass needle. It is always located along lines of tension.
There are very sensitive electronic devices that can easily detect the presence of electrostatic fields.
Electrostatic field potential
An electric field with intensity \( \vec{E} \) does work when moving a charge \( q \). The work \( A \) of the electrostatic field is calculated by the formula:
where \( d \) is the distance over which the charge moves, \( \alpha \) is the angle between the vectors of the electric field strength and the charge movement.
Important! This formula is applicable to finding work only in a uniform electrostatic field.
The work of electrostatic field forces when moving a charge from one point in the field to another does not depend on the shape of the trajectory, but is determined only by the initial and final position of the charge.
potential if the work done by forces to move a charge along a closed path is zero.
Important! The work done by the electrostatic field forces when moving a charge along any closed trajectory is zero. The electrostatic field is potential.
The work of the electrostatic field to move a charge is equal to the change in potential energy, taken with the opposite sign. In electrodynamics, energy is usually denoted by the letter \( W \), since the letter \( E \) denotes field strength:
The potential energy of a charge \( q \) placed in an electrostatic field is proportional to the magnitude of this charge. The potential energy of interaction of charges is calculated relative to the zero level (similar to the potential energy of the gravity field). The choice of the zero level of potential energy is determined based on considerations of convenience when solving the problem.
How does the length of vector E change with distance?
The length of the tension vector decreases rapidly with distance. This can be judged using a formula describing the module of a given vector:
\[\large E = k \cdot \frac {Q}{r^{2}} \]
The distance r is squared and placed in the denominator. This means that if the distance increases by 2 times, then the tension will decrease by 4 times.
And if, for example, the distance increases by 3 times, then the tension will decrease by 9 times.
Figure 9 shows the change in the length of the tension vector. Pay attention to the direction of this vector and the sign of the charge:
Rice. 9. How does the intensity depend on the distance to the charge that created the field?
We can express the dependence of tension on distance using the proportion sign:
\[\large E \sim \frac {1}{r^{2}} \]
A similar dependence on a graph can be reflected by the following curve:
Rice. 10. The modulus of the electric field strength vector decreases rapidly with increasing distance to the charge
As can be seen from Figure 10, increasing the distance to the charge by four times causes a weakening of its field strength by sixteen times.
Electric field potential. Potential difference
Potential is a scalar physical quantity equal to the ratio of the potential energy of an electric charge in an electrostatic field to the value of this charge.
The designation is \( \varphi \), the SI unit is volt (V).
Potential \(\varphi\) is an energy characteristic of the electrostatic field.
The potential difference is numerically equal to the work done by the electric force when moving a unit positive charge between two points of the field:
Designation – \( \Delta\varphi \), SI unit of measurement is volt (V).
Sometimes the potential difference is denoted by the letter \(U\) and is called voltage .
Important! Potential difference \(\Delta\varphi=\varphi_1-\varphi_2\), not potential change \(\Delta\varphi=\varphi_2-\varphi_1\). Then the work of the electrostatic field is:
Important! This formula allows you to calculate the work of electrostatic forces in any field.
In electrostatics, potential is often calculated relative to a point at infinity. In this case, the field potential at a given point is equal to the work done by electric forces when removing a unit positive charge from a given point to infinity.
The field potential of a point charge \( q \) at a point distant from it at a distance \( r \) is calculated by the formula:
To visually represent the electric field, equipotential surfaces are used.
Important! Inside a conducting ball, the potential of all points inside the ball is equal to the potential of the ball’s surface and is calculated using the formula for the potential of a point charge (\( r =R \), where \( R \) is the radius of the ball). The field strength inside the ball is zero.
An equipotential surface, or surface of equal potential, is a surface at all points of which the potential has the same value.
Properties of equipotential surfaces
- The tension vector is perpendicular to the equipotential surfaces and directed in the direction of decreasing potential.
- The work done to move a charge along an equipotential surface is zero.
In the case of a uniform field, equipotential surfaces are a system of parallel planes. For a point charge, the equipotential surfaces are concentric circles.
Potential difference and tension are related by the formula:
From the principle of superposition of fields follows the principle of superposition of potentials:
The potential of the resulting field is equal to the sum of the potentials of the fields of individual charges.
Important! Potentials are added algebraically, and tensions are added according to the rule of vector addition.
The solution of problems about point charges and systems that can be reduced to them is based on the application of conservation laws, the theorem on the change in the kinetic energy of a charge, taking into account the work of electrostatic forces.
Algorithm for solving such problems:
- establish the nature and features of electrostatic interactions of system objects;
- introduce the characteristics (force and energy) of these interactions, make a drawing;
- write down the laws of conservation and motion for objects;
- express the energy of electrostatic interaction through charges, potentials, tensions;
- create a system of equations and solve it relative to the desired value;
- check the solution.
Will the field act on a charge located between the lines of force?
Beginners studying electrostatics often have a question: will the charge located in the figure between the lines of force be affected by a force from the electric field? Of course it will be.
It doesn't matter whether the charge is on the field line in the drawing, or in the space between the field lines. The field exists at all points of the region under consideration, therefore the charge will be acted upon by a force at any point in the field, regardless of whether this point is on the line of force or not.
Note: Field lines are just a way to graphically represent a field in some region of space. The field exists at all points in space, and not just on lines of force.
Conductors in an electric field
Conductors are substances in which the ordered movement of electrical charges can occur, i.e., electric current can flow.
Conductors are metals, aqueous solutions of salts, acids, and ionized gases. Conductors contain free electrical charges. In metals, the valence electrons of atoms interacting with each other become free.
If a metal conductor is placed in an electric field, then under its action the free electrons of the conductor will begin to move in the direction opposite to the direction of the field strength. As a result, an excess negative charge will appear on one surface of the conductor, and an excess positive charge on the opposite surface.
These charges create an internal electric field inside the conductor, the intensity vector of which is directed opposite to the external field intensity vector. Under the influence of an external electrostatic field, conduction electrons in a metal conductor are redistributed so that the resulting field strength at any point inside the conductor is zero. Electric charges are located on the surface of the conductor.
Important! If there is a cavity inside the conductor, then the voltage in it will be zero regardless of what field is present outside the conductor and how charged the conductor is. The internal cavity in the conductor is shielded (protected) from external electrostatic fields. Electrostatic protection is based on this.
The phenomenon of charge redistribution in an external electrostatic field is called electrostatic induction .
Charges separated by an electrostatic field cancel each other out if the conductor is removed from the field. If such a conductor is cut without taking it out of the field, then its parts will have charges of different signs.
Important! At all points on the surface of the conductor, the voltage vector is directed perpendicular to its surface. The surface of the conductor is equipotential (the potentials of all points on the surface of the conductor are equal).
Dielectrics in an electric field
Dielectrics are substances that do not conduct electric current. Dielectrics are glass, porcelain, rubber, distilled water, and gases.
There are no free charges in dielectrics; all charges are bound. In a dielectric molecule, the total negative charge of the electrons is equal to the positive charge of the nucleus. There are polar and non-polar dielectrics.
In molecules of polar dielectrics, nuclei and electrons are located so that the centers of mass of positive and negative charges do not coincide and are at some distance from each other. That is, molecules represent dipoles regardless of the presence of an external electric field. In the absence of an external electric field, due to the thermal motion of molecules, the dipoles are located randomly, so the total field strength of all dielectric dipoles is zero.
If, in the absence of an external electric field, the centers of mass of positive and negative charges in a dielectric molecule coincide, then it is called non-polar. An example of such a dielectric is the hydrogen molecule. If such a dielectric is placed in an external electric field, then the directions of the force vectors acting on positive and negative charges will be opposite. As a result, the molecule is deformed and turns into a dipole. When a dielectric is introduced into an electric field, its polarization occurs.
Polarization of a dielectric is the process of displacement in opposite directions of unlike bound charges that make up the atoms and molecules of a substance in an electric field.
If the dielectric is non-polar, then a displacement of positive and negative charges occurs in its molecules. Surface bound charges will appear on the surface of the dielectric. These charges are called bound because they cannot move freely separately from each other.
Inside the dielectric, the total charge is zero, and on the surfaces the charges are not compensated and create a field inside the dielectric, the intensity vector of which is directed opposite to the external field strength vector. This means that inside the dielectric the field has a lower intensity than in a vacuum.
A physical quantity equal to the ratio of the modulus of the electric field strength in a vacuum to the modulus of the electric field strength in a homogeneous dielectric is called dielectric constant of a substance :
In a polar dielectric, in an external electric field, the dipoles rotate and they line up along the tension lines.
If a dielectric introduced into an electric field is cut, then its parts will be electrically neutral.
general characteristics
An electric field is a specific type of matter formed by microbodies that have charges. However, this is not only a collection of charged bodies: this term also refers to the microfield that forms each charged body in space. It is the combination of these microfields that creates electric fields in our usual understanding.
The existence and continuous functioning of the electric field is due to the continuous interaction of particles with charges, during which they directly impart electromagnetic energy to each other through the electric fields that surround each of them. Graphically, the electric field should be depicted as a schematic set of lines, called force lines in physical science.
Power lines
Thanks to the achievements of modern physics, we know that electrical forces explain all the chemical and physical properties of substances, from the atom to the animal cell. The naturalists who laid the foundation for the scientific knowledge of the electric field were Andre-Marie Ampère, Michael Faraday and James Clerk Maxwell.
Electrical capacity. Capacitor
Electric capacitance (electric capacity) is a scalar physical quantity that characterizes the ability of an isolated conductor to hold an electric charge.
The designation is \( C \), the SI unit is farad (F).
A solitary conductor is a conductor that is distant from other conductors and charged bodies.
Farad is the electrical capacity of such an isolated conductor, the potential of which changes by 1 V when a charge of 1 C is imparted to it:
Formula for calculating electrical capacity:
where \( q \) is the charge of the conductor, \( \varphi \) is its potential.
Electrical capacity depends on its linear dimensions and geometric shape. Electrical capacity does not depend on the material of the conductor and its state of aggregation. The electrical capacity of a conductor is directly proportional to the dielectric constant of the medium in which it is located.
A capacitor is a system of two conductors separated by a dielectric layer, the thickness of which is small compared to the size of the conductors.
The conductors are called capacitor plates. The charges of the capacitor plates are equal in magnitude and opposite in sign of charge. The electric field is concentrated between the plates of the capacitor. Capacitors are used to store electrical charges.
The electrical capacity of the capacitor is calculated by the formula:
where \( q \) is the charge modulus of one of the plates, \( U \) is the potential difference between the plates.
The electrical capacity of a capacitor depends on the linear dimensions and geometric shape and the distance between the conductors. The electrical capacity of a capacitor is directly proportional to the dielectric constant of the substance between the conductors.
A flat capacitor consists of two parallel plates of area \( S \) located at a distance \( d \) from each other.
Electrical capacity of a flat capacitor:
where \( \varepsilon \) is the dielectric constant of the substance between the plates, \( \varepsilon_0 \) is the electrical constant.
On the electrical diagram the capacitor is designated:
Types of capacitors:
- by type of dielectric - air, paper, etc.;
- shape – flat, cylindrical, spherical;
- by electrical capacity - constant and variable capacity.
Capacitors can be connected to each other.
Parallel connection of capacitors
In a parallel connection, capacitors are connected by similarly charged plates. The capacitor voltages are:
Total capacity:
Series connection of capacitors
When capacitors are connected in series, their oppositely charged plates are connected.
The charges of the capacitors with this connection are equal:
Total voltage:
The reciprocal of the total capacity:
With this connection, the total capacitance is always less than the capacitances of the individual capacitors.
Important! If a capacitor is connected to a current source, then the potential difference between its plates does not change when the electrical capacitance changes and is equal to the source voltage. If a capacitor is charged to a certain potential difference and is disconnected from the current source, then its charge does not change when the electrical capacitance changes.
Application of capacitors Capacitors are used in electronic devices as charge storage devices to smooth out ripples in AC rectifiers.
Michael Faraday and the birth of field physics
Yuliy Lvovich Mentsin “Quantum” No. 1, 2012
Michael Faraday, 1791–1867
September 22, 2011 marked the 220th anniversary of the birth of Michael Faraday (1791–1867), an English experimental physicist who introduced the concept of “field” into science and laid the foundations for the concept of the physical reality of electric and magnetic fields. These days, the concept of a field is familiar to any high school student. Basic information about electric and magnetic fields and methods of describing them using lines of force, tensions, potentials, etc. have long been included in school textbooks on physics. In the same textbooks you can read that a field is a special form of matter, fundamentally different from matter. But with an explanation of what exactly this “specialness” consists of, serious difficulties arise. Naturally, textbook authors cannot be blamed for this. After all, if the field is not reducible to some other, simpler entities, then there is nothing to explain. You just need to accept the physical reality of the field as an experimentally established fact and learn to work with the equations that describe the behavior of this object. For example, Richard Feynman calls for this in his Lectures, noting that scientists for a long time tried to explain the electromagnetic field using various mechanical models, but then abandoned this idea and considered that only the system of famous Maxwell’s equations describing the field had a physical meaning.
Does this mean that we should completely give up trying to understand what a field is? It seems that significant assistance in answering this question can be provided by acquaintance with “Experimental Studies in Electricity” by Michael Faraday - a grandiose three-volume work that the brilliant experimenter created for more than 20 years. It is here that Faraday introduces the concept of a field and, step by step, develops the idea of the physical reality of this object. At the same time, it is important about Faraday - one of the greatest books in the history of physics - written in excellent language, does not contain a single formula and is quite accessible to schoolchildren.
Field introduction. Faraday, Thomson and Maxwell
The term “field” (more precisely: “magnetic field”, “field of magnetic forces”) was introduced by Faraday in 1845 during research into the phenomenon of diamagnetism (the terms “diamagnetism” and “paramagnetism” were also introduced by Faraday) - the effect of weak repulsion by a magnet discovered by the scientist a number of substances. Initially, the field was considered by Faraday as a purely auxiliary concept, essentially a coordinate grid formed by magnetic lines of force and used to describe the nature of the movement of bodies near magnets. Thus, pieces of diamagnetic substances, for example bismuth, moved from areas of condensation of field lines to areas of their rarefaction and were located perpendicular to the direction of the lines.
William Thomson (Lord Kelvin), 1824–1907
Somewhat later, in 1851–1852, when mathematically describing the results of some of Faraday’s experiments, the term “field” was occasionally used by the English physicist William Thomson (1824–1907). As for the creator of the theory of the electromagnetic field, James Clerk Maxwell (1831–1879), in his works the term “field” also practically does not appear at first and is used only to designate that part of space in which magnetic forces can be detected. Only in the work “Dynamic Theory of the Electromagnetic Field” published in 1864–1865, in which the system of “Maxwell’s equations” first appears and predicts the possibility of the existence of electromagnetic waves propagating at the speed of light, is the field spoken of as a physical reality.
This is the brief history of the introduction of the concept of “field” into physics. It is clear from it that initially this concept was considered as a purely auxiliary one, denoting simply that part of space (it can be unlimited) in which magnetic forces can be detected and their distribution can be depicted using lines of force. (The term “electric field” came into use only after Maxwell’s theory of the electromagnetic field.)
It is important to emphasize that neither the lines of force known to physicists before Faraday, nor the field “consisting” of them were considered (and could not be considered!) by the scientific community of the 19th century as a physical reality. Attempts by Faraday to talk about the materiality of lines of force (or Maxwell - about the materiality of the field) were perceived by scientists as completely unscientific. Even Thomson, an old friend of Maxwell, who himself did a lot to develop the mathematical foundations of field physics (it was Thomson, and not Maxwell, who was the first to show the possibility of “translating” the language of Faraday’s force lines into the language of partial differential equations), called the theory of the electromagnetic field “mathematical nihilism” "and for a long time refused to recognize it. It is clear that Thomson could only do this if he had very serious reasons for doing so. And he had such reasons.
Force field and Newton's force
The reason why Thomson could not accept the reality of force lines and fields is simple. The lines of force of the electric and magnetic fields are defined as continuous lines drawn in space so that the tangents to them at each point indicate the directions of the electric and magnetic forces acting at that point. The magnitudes and directions of these forces are calculated using the laws of Coulomb, Ampere and Biot-Savart-Laplace. However, these laws are based on the principle of long-range action, which allows for the possibility of instantaneous transmission of the action of one body to another over any distance and, thereby, excluding the existence of any material intermediaries between interacting charges, magnets and currents.
James Clerk Maxwell, 1831–1879
It should be noted that many scientists were skeptical about the principle that bodies could somehow mysteriously act where they do not exist. Even Newton, who was the first to use this principle in deducing the law of universal gravitation, believed that some kind of substance could exist between interacting bodies. But the scientist did not want to build a hypothesis about it, preferring to develop mathematical theories of laws based on firmly established facts. Newton's followers did the same. According to Maxwell, they literally “swept out of physics” all sorts of invisible atmospheres and outflows with which proponents of the concept of short-range action surrounded magnets and charges in the 18th century. Nevertheless, in physics of the 19th century, interest in seemingly forever forgotten ideas is gradually beginning to revive.
One of the most important prerequisites for this revival was the problems that arose when trying to explain new phenomena - primarily the phenomena of electromagnetism - on the basis of the principle of long-range action. These explanations became increasingly artificial. Thus, in 1845, the German physicist Wilhelm Weber (1804–1890) generalized Coulomb’s law by introducing into it terms that determine the dependence of the force of interaction of electric charges on their relative velocities and accelerations. The physical meaning of such a dependence was not clear, and Weber’s additions to Coulomb’s law were clearly in the nature of a hypothesis introduced to explain the phenomena of electromagnetic induction.
In the mid-19th century, physicists increasingly realized that when studying the phenomena of electricity and magnetism, experiment and theory began to speak different languages. In principle, scientists were ready to agree with the idea of the existence of a substance that transmits the interaction between charges and currents at a finite speed, but they could not accept the idea of the physical reality of the field. First of all, because of the internal contradiction of this idea. The fact is that in Newtonian physics force is introduced as the cause of the acceleration of a material point. Its (force) magnitude is equal, as is known, to the product of the mass of this point and the acceleration. Thus, force as a physical quantity is determined at the point and at the moment of its action. “Newton himself reminds us,” wrote Maxwell, “that a force exists only as long as it acts; its effect may persist, but the force itself as such is essentially a transitory phenomenon.”
By trying to consider the field not as a convenient illustration of the nature of the distribution of forces in space, but as a physical object, scientists came into conflict with the original understanding of force on the basis of which this object was built. At each point, the field is determined by the magnitude and direction of the force acting on the test body (charge, magnetic pole, coil with current). In essence, the field “consists” only of forces, but the force at each point is calculated on the basis of laws according to which it is meaningless to talk about the field as a physical state or process. The field, considered as a reality, would mean the reality of forces existing outside of any action, which is completely contrary to the original definition of force. Maxwell wrote that in cases where we talk about “conservation of force”, etc., it would be better to use the term “energy”. This is certainly correct, but what is the energy of the field? By the time Maxwell wrote the above lines, he already knew that the energy density of, for example, an electric field is proportional to the square of the intensity of this field, i.e., again, the force distributed in space.
The concept of instantaneous action at a distance is inextricably linked with Newton’s understanding of force. After all, if one body acts on another, distant one, not instantly (essentially destroying the distance between them), then we will have to consider the force moving in space and decide what “part” of the force causes the observed acceleration and what meaning then has the concept "force". Or we must assume that the movement of force (or field) occurs in some special way that does not fit into the framework of Newtonian mechanics.
In 1920, in the article “Ether and the Theory of Relativity,” Albert Einstein (1879–1955) wrote that, speaking about the electromagnetic field as a reality, we must assume the existence of a special physical object, which in principle cannot be imagined as consisting of particles, the behavior of each of which is subject to study over time. Einstein later described the creation of the theory of the electromagnetic field as the greatest revolution in our views on the structure of physical reality since Newton. Thanks to this revolution, physics, along with ideas about the interaction of material points, included ideas about fields as irreducible entities to anything else.
But how was this change in views on reality possible? How did physics manage to go beyond its boundaries and “see” something that simply did not exist for it as a reality before?
Faraday's many years of experiments with power lines played an extremely important role in preparing this revolution. Thanks to Faraday, these lines, well known to physicists, turned from a way of depicting the distribution of electric and magnetic forces in space into a kind of “bridge”, moving along which it was possible to penetrate into the world that was, as it were, “behind the force”, into a world in which forces became manifestations of properties fields. It is clear that such a transformation required a very special kind of talent, the talent that Michael Faraday possessed.
Great Experimenter
Humphry Davy, 1778–1829
Michael Faraday was born on September 22, 1791 into the family of a London blacksmith, who, due to lack of funds, were unable to provide their children with an education. Michael, the third child in the family, did not finish primary school and at the age of 12 was sent as an apprentice to a bookbinding workshop. There he had the opportunity to read many books, including popular science, filling in the gaps in his education. Faraday soon began attending public lectures, which were regularly held in London to spread knowledge among the general public.
In 1812, one of the members of the Royal Society of London, who regularly used the services of a bookbindery, invited Faraday to listen to lectures by the famous physicist and chemist Humphry Davy (1778–1829). This moment became a turning point in Faraday's life. The young man became completely interested in science, and since his time in the workshop was ending, Faraday took the risk of writing to Davy about his desire to engage in research, enclosing carefully bound lecture notes from the scientist to the letter. Davy, who was himself the son of a poor woodcarver, not only responded to Faraday's letter, but also offered him a position as an assistant at the Royal Institution of London. Thus began Faraday’s scientific work, which continued almost until his death on August 25, 1867.
The history of physics knows many outstanding experimenters, but, perhaps, only Faraday was called an Experimenter with a capital letter. And it’s not just his colossal achievements, including the discoveries of the laws of electrolysis and the phenomena of electromagnetic induction, studies of the properties of dielectrics and magnets, and much more. Often important discoveries were made more or less by accident. The same cannot be said about Faraday. His research has always been strikingly systematic and purposeful. So, in 1821, Faraday wrote in his work diary that he was beginning a search for the connection between magnetism and electricity and optics. He discovered the first connection 10 years later (the discovery of electromagnetic induction), and the second - 23 years later (the discovery of the rotation of the plane of polarization of light in a magnetic field).
Faraday's Experimental Studies in Electricity contains about 3,500 paragraphs, many of which contain descriptions of experiments he performed. And this is only what Faraday saw fit to publish. In Faraday's multi-volume Diaries, which he kept since 1821, about 10 thousand experiments are described, and the scientist carried out many of them without anyone's help. Interestingly, in 1991, when the scientific world celebrated the 200th anniversary of Faraday's birth, English historians of physics decided to repeat some of his most famous experiments. But even simply reproducing each of these experiments required a team of modern specialists at least a day of work.
Speaking about Faraday's merits, we can say that his main achievement was the transformation of experimental physics into an independent field of research, the results of which can often be many years ahead of the development of theory. Faraday considered the desire of many scientists to move as quickly as possible from the data obtained in experiments to their theoretical generalization as extremely unproductive. It seemed more fruitful to Faraday to maintain a long-term connection with the phenomena being studied in order to be able to analyze in detail all their features, regardless of whether these features correspond to accepted theories or not.
Faraday extended this approach to the analysis of experimental data to the well-known experiments on aligning iron filings along magnetic field lines. Of course, the scientist knew very well that the patterns that form iron filings can easily be explained on the basis of the principle of long-range action. However, Faraday believed that in this case experimenters should proceed not from concepts invented by theorists, but from phenomena that, in his opinion, indicate the existence in the space surrounding magnets and currents of certain states that are ready for action. In other words, lines of force, according to Faraday, indicated that force should be thought of not only as an action (on a material point), but also as the ability to act.
It is important to emphasize that, following his methodology, Faraday did not try to put forward any hypotheses about the nature of this ability to act, preferring to gradually accumulate experience while working with lines of force. This work began in his studies of the phenomena of electromagnetic induction.
Delayed opening
In many textbooks and reference books you can read that on August 29, 1831, Faraday discovered the phenomenon of electromagnetic induction. Historians of science are well aware that dating discoveries is complex and often quite confusing. The discovery of electromagnetic induction is no exception. From Faraday's Diaries it is known that he observed this phenomenon back in 1822 during experiments with two conducting circuits placed on a soft iron core. The first circuit was connected to a current source, and the second to a galvanometer, which recorded the occurrence of short-term currents when the current in the first circuit was turned on or off. Later it turned out that other scientists had observed similar phenomena, but, like Faraday at first, they considered them an experimental error.
Faraday in the laboratory
The fact is that in searching for the phenomena of the generation of electricity by magnetism, scientists were aimed at discovering stable effects, similar, for example, to the phenomenon of the magnetic action of current discovered by Oersted in 1818. Faraday was saved from this general “blindness” by two circumstances. Firstly, close attention to any natural phenomena. In his articles, Faraday reported on both successful and unsuccessful experiments, believing that an unsuccessful experiment (which did not detect the desired effect), but a meaningful experiment also contained some information about the laws of nature. Secondly, shortly before the discovery, Faraday experimented a lot with capacitor discharges, which undoubtedly sharpened his attention to short-term effects. Regularly reviewing his diaries (for Faraday this was a constant part of his research), the scientist, apparently, took a fresh look at the experiments of 1822 and, having reproduced them, realized that he was dealing not with interference, but with the phenomenon he was looking for. The date of this realization was August 29, 1831.
Next, intensive research began, during which Faraday discovered and described the basic phenomena of electromagnetic induction, including the occurrence of induced currents during the relative motion of conductors and magnets. Based on these studies, Faraday came to the conclusion that the decisive condition for the occurrence of induced currents is precisely the intersection
a conductor of lines of magnetic force, and not a transition to areas of greater or lesser forces. In this case, for example, the occurrence of a current in one conductor when the current is turned on in another, located nearby, Faraday also explained as a result of the conductor crossing power lines: “magnetic curves seem to move (so to speak) across the induced wire, starting from the moment when they begin to develop, and up to the moment when the magnetic current reaches its greatest value; they seem to spread to the sides of the wire and, therefore, find themselves in relation to the stationary wire in the same position as if it were moving in the opposite direction across them.”
Let us pay attention to how many times in the above passage Faraday uses the words “as if”, and also to the fact that he does not yet have the usual quantitative formulation of the law of electromagnetic induction: the current strength in a conducting circuit is proportional to the rate of change in the number of magnetic lines of force passing through this circuit. A formulation close to this appears in Faraday only in 1851, and it applies only to the case of the movement of a conductor in a static magnetic field. According to Faraday, if a conductor moves in such a field at a constant speed, then the strength of the electric current arising in it is proportional to this speed, and the amount of electricity set in motion is proportional to the number of magnetic field lines crossed by the conductor.
Faraday's caution in formulating the law of electromagnetic induction is due, first of all, to the fact that he could correctly use the concept of a line of force only in relation to static fields. In the case of variable fields, this concept acquired a metaphorical character, and the continuous clauses “as if” when talking about moving lines of force show that Faraday understood this perfectly. He also could not help but take into account the criticism of those scientists who pointed out to him that a line of force is, strictly speaking, a geometric object, the movement of which is simply pointless to talk about. In addition, in experiments we deal with charged bodies, current-carrying conductors, etc., and not with abstractions like lines of force. Therefore, Faraday had to show that when studying at least some classes of phenomena, one cannot limit oneself to considering current-carrying conductors and not take into account the space surrounding them. Thus, in a work devoted to the study of self-induction phenomena, without ever mentioning lines of force, Faraday builds a story about his experiments in such a way that the reader gradually comes to the conclusion that the real cause of the observed phenomena is not current-carrying conductors, but something located in the space surrounding them.
The field is like a premonition. Research into self-induction phenomena
In 1834, Faraday published the ninth part of his Experimental Investigations, which was entitled “On the inductive influence of an electric current on itself and on the inductive action of currents in general.” In this work, Faraday examined the phenomena of self-induction, discovered in 1832 by the American physicist Joseph Henry (1797–1878), and showed that they represent a special case of the phenomena of electromagnetic induction he had previously studied.
Faraday begins his work by describing a series of phenomena, consisting in the fact that when an electrical circuit containing long conductors or an electromagnet winding is opened, a spark appears at the point where the contact is broken, or an electric shock is felt if the contact is separated by hand. At the same time, Faraday points out, if the conductor is short, then no amount of trickery can produce a spark or electric shock. Thus, it became clear that the occurrence of a spark (or impact) depends not so much on the strength of the current flowing through the conductor before the contact was broken, but on the length and configuration of this conductor. Therefore, Faraday first of all seeks to show that, although the initial cause of the spark is current (if there was no current in the circuit at all, then, naturally, there will be no spark), the strength of the current is not decisive. To do this, Faraday describes a sequence of experiments in which the length of the conductor is first increased, resulting in a stronger spark despite the weakening of the current in the circuit due to the increased resistance. This conductor is then twisted so that current flows only through a small part of it. The current increases sharply, but the spark disappears when the circuit is opened. Thus, neither the conductor itself nor the strength of the current in it can be considered as the cause of the spark, the magnitude of which, as it turns out, depends not only on the length of the conductor, but also on its configuration. So, when the conductor is rolled into a spiral, as well as when an iron core is introduced into this spiral, the spark size also increases.
In continuation of the study of these phenomena, Faraday connected an auxiliary short conductor parallel to the place where the contact was opened, the resistance of which was significantly greater than that of the main conductor, but less than that of the spark gap or the body of the person opening the contact. As a result, the spark disappeared when the contact was opened, and a strong short-term current arose in the auxiliary conductor (Faraday calls it an extra current), the direction of which turned out to be opposite to the direction of the current that would flow through it from the source. “These experiments,” writes Faraday, “establish an essential difference between the primary or exciting current and the extra current in respect of quantity, intensity, and even direction; they led me to the conclusion that the extracurrent is identical with the induced current I described earlier.”
Having put forward the idea of a connection between the phenomena being studied and the phenomena of electromagnetic induction, Faraday then carried out a series of ingenious experiments confirming this idea. In one of these experiments, next to a spiral connected to a current source, another open spiral was placed. When disconnected from the current source, the first spiral gave a strong spark. However, if the ends of the other spiral were closed, the spark practically disappeared, and a short-term current arose in the second spiral, the direction of which coincided with the direction of the current in the first spiral if the circuit was opened, and was opposite to it if the circuit was closed.
Having established the connection between the two classes of phenomena, Faraday was able to easily explain the experiments performed earlier, namely, the intensification of the spark when the conductor is lengthened, folded into a spiral, an iron core is introduced into it, etc.: “If you observe the inductive effect of a wire one foot long on a located there is a wire nearby that is also one foot long, then it turns out to be very weak; but if the same current be passed through a wire fifty feet long, it will induce in the next fifty feet of wire, at the moment of making or breaking a contact, a much stronger current, as if every extra foot of wire contributed something to the total effect; By analogy, we conclude that the same phenomenon must also occur when the connecting conductor simultaneously serves as a conductor in which an induced current is formed.” Therefore, Faraday concludes, increasing the length of the conductor, rolling it into a spiral and introducing a core into it strengthens the spark. The action of the demagnetizing core is added to the action of one turn of the spiral on another. Moreover, the totality of such actions can compensate for each other. For example, if you fold a long insulated wire in half, then due to the opposite inductive actions of its two halves, the spark will disappear, although in the straightened state this wire gives a strong spark. The replacement of an iron core with a steel core, which demagnetizes very slowly, also led to a significant weakening of the spark.
So, guiding the reader through detailed descriptions of the sets of experiments performed, Faraday, without saying a word about the field, formed in him, the reader, the idea that the decisive role in the phenomena being studied does not belong to conductors with current, but to some kind of force created by them in the surrounding space. then the state of magnetization, or more precisely, the rate of change of this state. However, the question of whether this state really exists and whether it can be the subject of experimental research remained open.
The problem of the physical reality of force lines
Faraday managed to take a significant step in proving the reality of field lines in 1851, when he came up with the idea of generalizing the concept of a field line. “A magnetic line of force,” wrote Faraday, “may be defined as the line which a small magnetic needle describes when it is moved in one direction or another in the direction of its length, so that the needle remains tangent to the motion all the time; or, in other words, this is the line along which a transverse wire can be moved in any direction and no tendency to generate any current will appear in the latter, whereas when moving it in any other direction such a tendency exists.”
The line of force was thus defined by Faraday on the basis of two different laws (and understandings) of the action of magnetic force: its mechanical action on the magnetic needle and its ability (in accordance with the law of electromagnetic induction) to generate electric force. This double definition of the line of force seemed to “materialize” it, giving it the meaning of special, experimentally detectable directions in space. Therefore, Faraday called such lines of force “physical,” believing that he could now definitively prove their reality. A conductor in such a double definition could be imagined as closed and sliding along the lines of force so that, while constantly deforming, it does not intersect the lines. This conductor would highlight a certain conditional “number” of lines that are preserved when they are “condensed” or “rarefied.” Such a sliding of a conductor in a field of magnetic forces without the emergence of an electric current in it could be considered as experimental proof of the conservation of the number of lines of force as they “spread,” for example, from the pole of a magnet, and, thus, as proof of the reality of these lines.
Rice. 1
Of course, it is almost impossible to move a real conductor so that it does not cross the power lines. Therefore, Faraday justified the hypothesis about the conservation of their number differently. Let a magnet with pole N and conductor abcd
are located so that they can rotate relative to each other around the
ad
(Fig. 1; the drawing was made by the author of the article based on Faraday’s drawings).
In this case, part of the conductor ad
passes through the hole in the magnet and has free contact at point
d
.
A free contact is also made at point c
, so that section
bc
can rotate around the magnet without breaking the electrical circuit connected at points
a
and
b
(also through sliding contacts) to the galvanometer.
The conductor bc
, with a complete rotation around the axis
ad
, intersects all lines of force emerging from the pole of the magnet N. Now let the conductor rotate at a constant speed.
Then, comparing the readings of the galvanometer at different positions of the rotating conductor, for example, in position abcd
and in position
ab'c'd
, when the conductor again crosses all lines of force for a full turn, but in places where they are more rarefied, one can find that the readings of the galvanometer are the same . According to Faraday, this indicates the preservation of a certain conditional number of lines of force that can characterize the north pole of a magnet (the larger this “quantity,” the stronger the magnet).
Rotating in his installation (Fig. 2; Faraday's drawing) not a conductor, but a magnet, Faraday comes to the conclusion that the number of lines of force in the internal region of the magnet is conserved. Moreover, his reasoning is based on the assumption that the lines of force are not carried away by a rotating magnet. These lines remain “in place” and the magnet rotates among them. In this case, the current is the same in magnitude as when the external conductor rotates. Faraday explains this result by saying that although the outer part of the conductor does not intersect the lines, its inner part ( cd
), rotating with the magnet, intersects all the lines passing inside the magnet. If the outer part of the conductor is fixed and rotated together with the magnet, then no current arises. This can also be explained. Indeed, the inner and outer parts of the conductor cross the same number of lines of force directed in the same direction, so the currents induced in both parts of the conductor cancel each other out.
Rice. 2
From the experiments it followed that inside the magnet the lines of force do not go from the north pole to the south, but on the contrary, forming closed curves with the external lines of force, which allowed Faraday to formulate the law of conservation of the number of magnetic lines of force in the external and internal spaces of a permanent magnet: “With this amazing distribution forces, which is revealed by a moving conductor, a magnet is exactly like an electromagnetic coil, both in that the lines of force flow in the form of closed circles, and in the equality of their sum inside and outside.” Thus, the concept of “number of power lines” received citizenship rights, due to which the formulation of the law of proportionality of the electromotive force of induction to the number of power lines crossed by a conductor per unit time acquired physical meaning.
However, Faraday admitted that his results were not conclusive proof of the reality of field lines. For such a proof, he wrote, it is necessary to “establish the relationship of the lines of force to time,” that is, to show that these lines can move in space with a finite speed and, therefore, can be detected by some physical methods.
It is important to emphasize that for Faraday the problem of “physical lines of force” had nothing in common with attempts to directly detect ordinary lines of force. Since the discovery of electromagnetic induction, Faraday believed that both ordinary lines of force and the laws of electromagnetism are manifestations of some special properties of matter, its special state, which the scientist called electrotonic. At the same time, the question of the essence of this state and its connection with known forms of matter was, Faraday believed, open: “What this state is and what it depends on, we cannot say now. Perhaps it is conditioned by the ether, like a light ray... Perhaps it is a state of tension, or a state of vibration, or some other state analogous to electric current, with which magnetic forces are so closely related. Whether the presence of matter is necessary to maintain this state depends on what is meant by the word “matter.” If the concept of matter is limited to weighty or gravitating substances, then the presence of matter is as little significant for the physical lines of magnetic force as for the rays of light and heat. But if, admitting the ether, we accept that this is a kind of matter, then the lines of force can depend on any of its actions.”
Such close attention that Faraday paid to power lines was primarily due to the fact that he saw in them a bridge leading to some completely new world. However, it was difficult for even such a brilliant experimenter as Faraday to cross this bridge. Actually, this problem did not allow for a purely experimental solution at all. However, one could try to penetrate mathematically into the space between the lines of force. This is exactly what Maxwell did. His famous equations became the tool that made it possible to penetrate into the non-existent gaps between Faraday's field lines and, as a result, discover a new physical reality there. But this is another story - the story of the Great Theorist.
This refers to the book by R. Feynman, R. Leighton and M. Sands “Feynman Lectures on Physics” (M.: Mir, 1967) ( Ed. note.
) In Russian translation, the first volume of this book was published in 1947, the second in 1951, and the third in 1959 in the series “Classics of Science” (M.: Publishing House of the USSR Academy of Sciences).
( Editor's note
) In 1892, William Thomson was awarded the noble title "Lord Kelvin" for fundamental work in various fields of physics, in particular on the laying of the transatlantic cable connecting England and the United States.
Electric field energy of a capacitor
The energy of a charged capacitor is equal to the work of external forces that must be expended to charge the capacitor.
The electrical energy of a capacitor is concentrated in the space between the plates of the capacitor, that is, in the electric field, therefore it is called electric field energy . Formulas for calculating the electric field energy:
Since the electric field strength is directly proportional to the voltage, the energy of the electric field of the capacitor is proportional to the square of the strength.
Electric field energy density:
where \( V \) is the volume of space between the plates of the capacitor.
The energy density does not depend on the parameters of the capacitor, but is determined only by the electric field strength.
Basic formulas of the section “Electric field”
Laws of direct current →
← Thermodynamics
Electric field
3 (59.79%) 94 votes