Example task No. 2
A nickelin wire with a length of $120 \space m$ and a cross-sectional area of $0.5 \space mm^2$ is connected to a circuit with a voltage of $127 \space V$. Determine the current strength in the wire.
The tabulated resistivity value of nickel is $0.4 \frac{Ohm \cdot mm^2}{m}$.
Let's move on to writing the conditions of the problem and its solution.
Given: $l = 120 \space m$ $S = 0.5 \space mm^2$ $U = 127 \space B$ $\rho = 0.4 \frac{Ohm \cdot mm^2}{m}$
$I — ?$
Solution:
We can calculate the current strength using the formula of Ohm's law for a section of the circuit: $I = \frac{U}{R}$.
But we do not know the resistance value of the conductor. We can also calculate it: $R = \frac{\rho \cdot l}{S}$, $R = \frac{0.4 \frac{Ohm \cdot mm^2}{m} \cdot 120 \space m} {0.5 \space mm^2} = \frac{48 \space Ohm}{0.5} = 96 \space Ohm$.
Now we can calculate the current strength: $I = \frac{127 \space V}{96 \space Ohm} \approx 1.3 \space A$.
Answer: $I \approx 1.3 \space A$.
Example problem #3
A manganin wire with a length of $8 \space m$ and a cross-sectional area of $0.8 \space mm^2$ is included in the battery circuit. The current strength in the circuit is $0.3 \space A$. Determine the voltage at the battery poles.
The tabulated value of the resistivity of manganin is $0.43 \frac{Ohm \cdot mm^2}{m}$.
Let's write down the conditions of the problem and solve it.
Given: $l = 8 \space m$ $S = 0.8 \space mm^2$ $I = 0.3 \space A$ $\rho = 0.43 \frac{Ohm \cdot mm^2}{m}$
$U — ?$
Solution:
If the problem statement says that the conductor is connected to the battery circuit, this means that the voltage at the battery poles will be equal to the voltage at the ends of the wire.
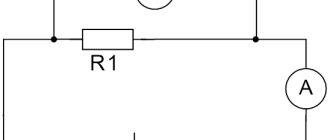
Why? Take a look at this electrical circuit (Figure 1). It consists only of a conductor and a battery.
Figure 1. Conductor connected to battery
If we want to measure the voltage at the battery poles using a voltmeter, we will connect it in parallel to this circuit (Figure 2). What if we want to measure the voltage at the ends of the conductor? We will connect the voltmeter in the same way. It turns out that the voltmeter is connected in parallel to both the current source and the conductor . Therefore, the voltage at the ends of the conductor is the same voltage at the battery poles.
Figure 2. Measuring voltage with a voltmeter at the poles of the current source and at the ends of the conductor
Let's write Ohm's law: $I = \frac{U}{R}$.
Let us express from it the voltage that needs to be found: $U = IR$.
We calculate the conductor resistance using the formula $R = \frac{\rho \cdot l}{S}$. $R = \frac{0.43 \frac{Ohm \cdot mm^2}{m} \cdot 8 \space m}{0.8 \space mm^2} = \frac{3.44 \space Ohm}{0.8} = 4.3 \ space Ohm$.
Now we can calculate the voltage: $U = 0.3 \space A \cdot 4.3 \space Ohm = 1.29 \space V \approx 1.3 \space V$.
Answer: $U \approx 1.3 \space B$.
How to determine a person's strength?
Strength formula:
- Force
(F) = m X a; - Mass (m) = F/a;
- Acceleration (a) = F/m;
Interesting materials:
Why doesn't water flow in a big circle? Why doesn't the water freeze under? Why doesn't water freeze completely? Why doesn't water freeze at sub-zero temperatures? Why does water expand when it turns into ICE? Why is there water in the muffler? Why does the water in the river freeze only at the top? Why does water freeze at 0 degrees? Why does water freeze first near the coast? Why do wolves howl at the moon?
Overcoming Various Friction
For example, a car has a fifty horsepower engine. When the driver presses the gas all the way, the engine crankshaft begins to make three thousand six hundred revolutions per minute. The pistons are rushing up and down like crazy, the valves are jumping, the gears are spinning, and the car is moving, although very quickly, but completely evenly, and the entire traction force of the engine is spent on overcoming the forces of resistance to movement, in particular, overcoming various friction
. Here, for example, is how the traction force of an engine is distributed between its “opponents” - different types at a car speed of one hundred kilometers per hour:
- About sixteen percent of the motor's traction force is spent on overcoming friction in the bearings and between gears,
- to overcome the friction of rolling wheels on the road - approximately twenty-four percent,
- Sixty percent of the car's traction force is spent on overcoming air resistance.
Windage
When considering motion resistance forces such as:
- sliding friction decreases slightly with increasing speed,
- rolling friction changes very little,
- air resistance
, completely imperceptible when moving slowly, becomes a formidable braking force when the speed increases.
Air turns out to be the main enemy of fast movement
.
Therefore, the bodies of cars, diesel locomotives, and the deck superstructures of steamships are given a rounded, streamlined shape, all protruding parts are removed, and they try to make sure that air can flow smoothly around them. When they build racing cars and want to achieve the highest speed from them, they borrow the shape of a fish’s body for the body of the car, and an engine with a capacity of several thousand horsepower is installed on such a high-speed car. But no matter what the inventors do, no matter how they improve the streamlining of the body, every movement is always followed, like a shadow, by the forces of friction and resistance of the environment. And even if they do not increase, they remain constant, the car will still have a speed limit. This is explained by the fact that the power of a machine is the product of traction force and its speed
. But since the movement is uniform, the traction force is entirely spent on overcoming various resistance forces. If these forces are reduced, then with a given power the machine will be able to develop greater speed. And since the main enemy of movement at high speeds is air resistance, designers have to be so sophisticated to combat it.
Artillerymen became interested in air resistance
Artillerymen were
primarily air resistance .
They tried to understand why cannon shells did not fly as far as they would like. Calculations showed that if there was no air on Earth, a seventy-six-millimeter cannon shell would fly at least twenty-three and a half kilometers
, but in reality it falls only
seven kilometers from the cannon
.
Sixteen and a half kilometers of range
are lost due to air resistance . It's a shame, but there's nothing you can do about it! Artillerymen improved guns and shells, guided mainly by guesswork and ingenuity. What happens to the projectile in the air was initially unknown. I would like to look at a flying projectile and see how it cuts through the air, but the projectile flies very quickly, the eye cannot catch its movement, and the air is even more invisible. The wish seemed impossible, but photography came to the rescue. By the light of an electric spark, it was possible to photograph a flying bullet. The spark flashed and momentarily illuminated the bullet flying in front of the camera lens. Its brilliance was enough to capture a snapshot of not only the bullet, but also the air it was cutting through. The photograph showed dark stripes extending from the bullet to the sides. Thanks to photographs, it became clear what happens when a projectile flies in the air. When an object moves slowly, the air particles calmly part in front of it and almost do not interfere with it, but when it moves quickly, the picture changes, the air particles no longer have time to fly apart. The projectile flies and, like a pump piston, drives air in front of it and compacts it. The higher the speed, the greater the compression and compaction. In order for the projectile to move faster and better penetrate the compacted air, its head is made pointed.
Swirl strip of air
In the photograph of the flying bullet, it was clear that a strip of swirling air
.
Part of the energy of a bullet or projectile is also spent on the formation of vortices. Therefore, the bottom of shells and bullets began to be made beveled, this reduced the resistance to movement in the air. Thanks to the beveled bottom, the range of the seventy-six-millimeter cannon projectile reached eleven to twelve kilometers
.
Friction of air particles
When flying in the air, the speed of movement is also affected by the friction of air particles against the walls of a flying object. This friction is small, but it still exists and heats the surface. Therefore, we have to paint airplanes with glossy paint and cover them with a special aviation varnish. Thus, the forces of resistance to movement in the air of all moving objects arise due to three different phenomena:
- air seals in front,
- formation of vortices behind,
- slight air friction on the side surface of the object.
Exercises
Exercise No. 1
The length of one wire is $20 \space cm$, the other is $1.6 \space m$.
The cross-sectional area and material of the wires are the same. Which wire has more resistance and by how much? Please note that if the material of the conductors is the same, then the resistivity values $\rho$ for these conductors are also the same.
Given: $l_1 = 20 \space cm$ $l_2 = 1.6 \space m$ $S_1 = S_2 = S$ $\rho_1 = \rho_2 = \rho$
SI: $l_1 = 0.2 \space m$
$\frac{R_2}{R_1} — ?$
Show solution and answer
Hide
Solution: The conductor resistance is calculated using the formula $R = \frac{\rho \cdot l}{S}$.
Resistance of the first wire: $R_1 = \frac{\rho_1 l_1}{S_1} = \frac{\rho l_1}{S}$.
Resistance of the second wire: $R_2 = \frac{\rho_2 l_2}{S_2} = \frac{\rho l_2}{S}$.
Now let's compare them to each other: $\frac{R_2}{R_1} = \frac{\frac{\rho l_2}{S}}{\frac{\rho l_1}{S}} = \frac{l_2}{l_1 }$.
Let's substitute the numerical values of the wire lengths: $\frac{R_2}{R_1} = \frac{1.6 \space m}{0.2 \space m} = 8$.
It turns out that the resistance of the second wire is 8 times greater than the resistance of the first .
This is logical, because you know that the longer the conductor, the greater its resistance .
Answer: the resistance of the second wire is 8 times greater than the resistance of the first.
Exercise No. 2
Calculate the resistance of the following conductors made:
- Made of aluminum wire with a length of $80 \space cm$ and a cross-sectional area of $0.2 \space mm^2$
- Made of nickel wire with a length of $400 \space cm$ and a cross-sectional area of $0.5 \space mm^2$
- Made of constantan wire with a length of $50 \space cm$ and a cross-sectional area of $0.005 \space cm^2$
To solve this problem, we will need tabulated resistivity values for the substances from which the wires are made. Resistivity of aluminum - $0.028 \frac{Ohm \cdot mm^2}{m}$, nickel - $0.4 \frac{Ohm \cdot mm^2}{m}$, constantan - $0.5 \frac{Ohm \cdot mm^2 }{m}$.
Pay attention to the units of measurement of resistivity, lengths and areas of conductors. For correct calculations, we will convert the length of each wire to SI (in $m^2$). Cross-sectional areas should be expressed in $mm^2$. For the third task, let's convert $cm^2$ to $cm^2$.
Given: $l_1 = 80 \space cm$ $l_2 = 400 \space cm$ $l_3 = 50 \space cm$ $S_1 = 0.2 \space mm^2$ $S_2 = 0.5 \space mm^2$ $S_3 = 0.005 \space cm^2 = 0.5 \space mm^2$ $\rho_1 = 0.028 \frac{Ohm \cdot mm^2}{m}$ $\rho_2 = 0.4 \frac{Ohm \cdot mm^2}{m} $ $\rho_3 = 0.5 \frac{Ohm \cdot mm^2}{m}$
SI: $l_1 = 0.8 \space m$ $l_2 = 4 \space m$ $l_3 = 0.5 \space m$
$R_1 — ?$ $R_2 — ?$ $R_3 — ?$
Show solution and answer
Hide
Solution:
The formula for calculating the resistance of a conductor is: $R = \frac{\rho l}{S}$. Let us calculate the resistance of each conductor from it.
$R_1 = \frac{\rho_1 l_1}{S_1}$, $R_1 = \frac{0.028 \frac{Ohm \cdot mm^2}{m} \cdot 0.8 \space m}{0.2 \space mm^2} = \frac{0.0224 \space Ohm}{0.2} = 0.112 \space Ohm$.
$R_2 = \frac{\rho_2 l_2}{S_2}$, $R_2 = \frac{0.4 \frac{Ohm \cdot mm^2}{m} \cdot 4 \space m}{0.5 \space mm^2} = \frac{1.6 \space Ohm}{0.5} = 3.2 \space Ohm$.
$R_3 = \frac{\rho_3 l_3}{S_3}$, $R_2 = \frac{0.5 \frac{Ohm \cdot mm^2}{m} \cdot 0.5 \space m}{0.5 \space mm^2} = \frac{0.25 \space Ohm}{0.5} = 0.5 \space Ohm$.
Answer: $R_1 = 0.112 \space Ohm$, $R_2 = 3.2 \space Ohm$, $R_3 = 0.5 \space Ohm$.
Exercise #3
The spiral of the electric hotplate is made of nichrome wire with a length of $13.75 \space m$ and a cross-sectional area of $0.1 \space mm^2$.
The tile is designed for a voltage of $220 \space V$. Determine the current strength in the tile spiral. The resistivity of nichrome is $1.1 \frac{Ohm \cdot mm^2}{m}$.
Given: $l = 13.75 \space m$ $S = 0.1 \space mm^2$ $U = 220 \space V$ $\rho = 1.1 \frac{Ohm \cdot mm^2}{m}$
$I — ?$
Show solution and answer
Hide
Solution:
We can calculate the current strength in the tile spiral using the formula of Ohm's law for a section of the circuit: $I = \frac{U}{R}$.
Let us calculate the unknown resistance of the nichrome wire using the formula $R = \frac{\rho l}{S}$. $R = \frac{1.1 \frac{Ohm \cdot mm^2}{m} \cdot 13.75 \space m}{0.1 \space mm^2} = \frac{15.125 \space Ohm}{0.1} = 151.25 \ space Ohm$.
Let us now calculate the current strength: $I = \frac{220 \space V}{151.25 \space Ohm} \approx 1.5 \space A$.
Answer: $I \approx 1.5 \space A$.
What is resistance?
Resistance (electrical resistance) is the property of a conductor to resist an electric current passing through it.
It's that simple! Let's make an analogy with hydraulics. In our case, it turns out that the conductor of electric current is a hose or pipe. Now let's think about which object will provide more resistance to the flow of water: a garden hose or an oil pipe?
It is clear that it is a garden hose, since its diameter is several times smaller than the diameter of an oil pipe.
Then another question. Which hose will have greater resistance to water flow, given that their lengths and diameters are equal?
Corrugated, of course. Water will “cling” to its walls, causing them to interfere with the flow of water.
Then here's another problem. There are two absolutely identical hoses, but one is longer and the other is shorter. Which hose will offer more resistance to water flow?
I think the one that is longer. The answer is obvious.